基于灰色聚类评估的配送中心选址模糊多目标优化模型

李 志， 江 舟， 周愉峰



基于灰色聚类评估的配送中心选址模糊多目标优化模型

李 志1， 江 舟2， 周愉峰1

(重庆工商大学 1. 重庆市发展信息管理工程技术研究中心; 2.电子商务及供应链系统重庆市重点实验室，重庆 400067)

将多属性决策方法与最优化方法相集成，研究了多配送中心选址优化问题。首先采用灰色聚类决策计算各候选地定性属性的综合评估值。再以选定配送中心的评估值均值最大化、系统成本最小化，以及配送中心容量利用率最大化作为3个优化目标，建立一个考虑需求点模糊需求、供应点与候选配送中心容量限制的三级供应链系统多配送中心选址模型。该模型被描述成了一个多目标的非线性混合整数规划模型。采用机会约束规划对模糊需求进行清晰化处理，并应用目标加权的方法将问题转化为单目标问题。通过算例验证了所提模型的可行性。在实际工作中，可根据决策者权重偏好得出令人满意的结果。

配送中心； 选址； 灰色聚类评估； 多目标优化模型

配送中心选址是物流系统规划中的一个重要问题。长期以来，研究者们主要从两个角度对该问题展开研究。一是基于多属性决策，建立一系列定性与定量评估指标集，并应用AHP[1]、模糊综合评估[2]、模糊AHP[2]、TOPSIS[3]等方法进行多属性综合评估。多属性决策方法可以考虑众多因素，考量周全。但在本质上属于定性决策，不可避免地受到人为因素的影响，客观性较差。鉴于此，也有大量文献从另一个角度，基于数学规划等最优化方法(主要是整数规划与混合整数规划)来定量研究该问题。例如，Gutjahr等[4]建立了一个物流配送中心选址的两目标双层规划模型。Neema等[5]建立了一个多目标设施选址模型，并研究了求解其Pareto前沿面的遗传算法。Amin等[6]研究了闭环供应链系统中的随机多目标设施选址问题，并建立了相应的混合整数规划模型。

但最优化方法仅能考虑成本、距离、满意度等易于量化处理的因素，而对大量定性属性难以综合考虑。因此，少量文献开始将最优化方法与多属性决策方法相集成，兼顾选址决策的各方面因素和量化约束，以期得到更加合理的选址方案。例如，Badri[7]研究了结合AHP和多目标规划的设施选址-分配问题。Liu等[8]基于非线性规划模型得出初选方案，再运用模糊综合评估法考虑政策环境等因素确定最终选址，结合实例检验了方法的可行性。莫海熙等[9]将候选地址的综合评估值作为其权重值，设计了一个带权重值约束条件的目标规划模型。张华等[10]运用粗糙集方法，对候选地址进行评估，得出候选地址评估值，建立了最大化综合评估值和最小化建设成本的双目标选址模型。Ozgen等[11]通过线性规划和FAHP法两种方法，构建了成本最小化和模糊评估值最大化的双目标选址模型。

本文也采用多属性决策方法与最优化方法相集成的思想，研究多配送中心选址优化问题。现实生活中，由于受到认知局限、信息完备性等因素的制约，人们对配送中心选址决策属性的认知具有明显的灰色性。同时，需求点的需求量受市场因素、经营因素等影响具有一定的模糊性。鉴于此，在灰色聚类综合评估值的基础上进一步构建配送中心选址的多目标模糊优化模型。首先，基于灰色聚类决策计算各候选地的综合评估值，再以各配送中心的评估值均值最大化、系统成本最小化，以及配送中心容量利用率最大化作为3个优化目标，建立一个考虑需求点具有模糊需求、供应点与候选配送中心具有容量限制的三级供应链系统多配送中心选址模型。对此，采用混合整数规划方法来描述模型。最后，设置了一个算例验证了所提模型的合理性。

1 基于灰色聚类决策的候选配送中心综合评估

1.1 构建评估指标体系

影响配送中心选址的因素众多，这些影响因素可以分为定性和定量两大类。首先剔除成本因素，构建配送中心选址评估指标体系[12](表1)。

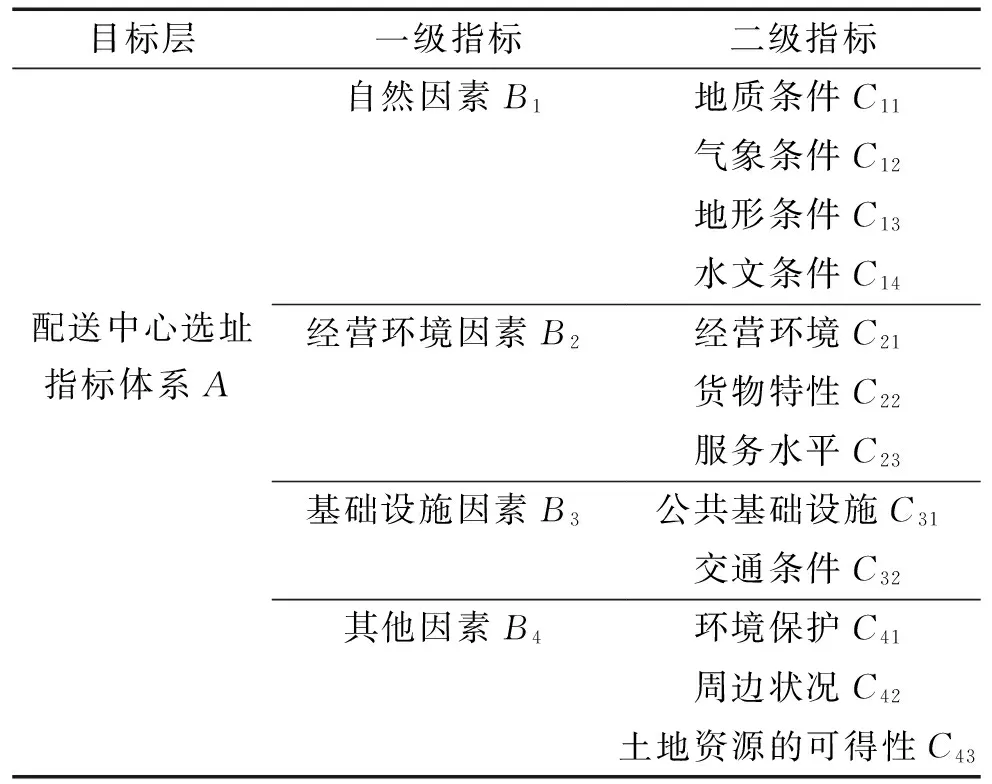
表1 候选配送中心的评估指标体系

1.2 确定指标权重

指标权重可通过AHP、专家调查等方法得到。

1.3 确定评估样本矩阵

令dij表示第i个评估者在第j个二级评估指标下给出的评估值，并将此作为各评估对象的评估样本矩阵

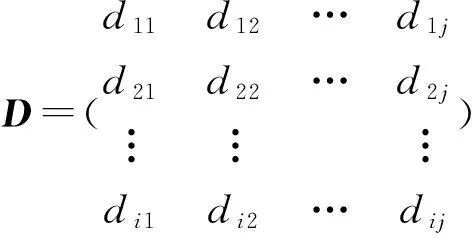
(1)

1.4 确定评估灰类

在得到评估值矩阵之后要根据评分情况对评估的灰类、灰类的等级、灰类的灰数以及灰数的白化权函数进行确定。

1.5 计算灰色评估系数

计算灰色评估系数。对某一评估对象进行评估，在二级指标j下，属于第h灰类的评估系数

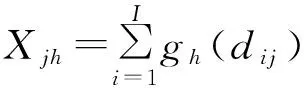
(2)

其中，gh(·)表示灰类白化权函数。

计算总灰色评估系数。对于评估对象在评估指标j属于1,2…,H灰类的总的评估系数

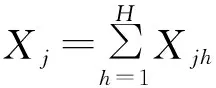
(3)

1.6 计算灰色评估权向量及权矩阵

由评估对象对于评估指标j属于第h灰类的评估系数Xjh和总的灰色评估系数Xj可以计算出评估对象对于评估指标j属于第h灰类的评估权

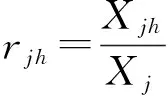
(4)

由此推及所有h=1,2,…,H灰类，得出在评估指标j下，评估对象的灰色评估权行向量

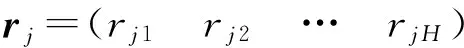
(5)

依照以上步骤，求得在所有的评估指标j=1,2,3，…，J下评估对象的灰色评估权矩阵

(6)

1.7 综合评估

对各一级指标进行综合评估，将二级指标权系数行向量w与对应的灰色评估权矩阵R相乘得到各一级指标的灰类评估权矩阵。

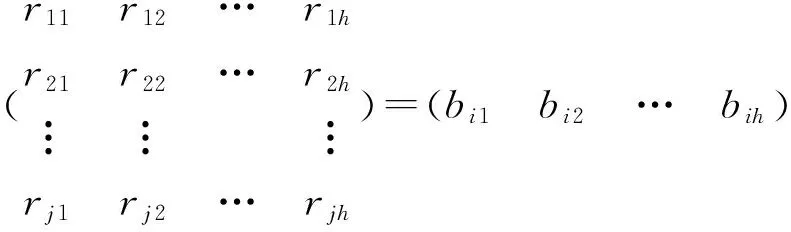
(7)

对候选配送中心进行综合评估，将目标层下的一级指标权系数行向量W与一级指标的灰类评估权矩阵bi相乘得到最终候选配送中心的灰类评估结果：

。

(8)

按照各评估灰类所属的评估等级进行赋值，确定各灰类赋值向量E=(e1,e2,…,eh)T，综合评估值的计算则可以表达为

s1=G×E。

(9)

按此步骤依次对第2,3,…,k个评估对象进行综合评估，得出各候选地址的综合评估结果s1,s2,…,sk，用于后续分析。

2 基于灰色聚类评估的配送中心选址多目标模糊优化模型

2.1 问题描述

在灰色聚类综合评估值的基础上进一步构建配送中心选址的多目标模糊优化模型。研究的是三级供应链系统中的多配送中心选址问题。系统中存在有多个供应点、多个候选配送中心以及需求点。供应点与配送中心均有容量限制。需求点的需求量具有一定的模糊性。配送中心的选址受到多种因素的影响。有些因素可以通过数学规划量化表示，例如建设成本、运输配送成本、运营管理成本等成本因素、配送中心的容量利用率。针对这些因素构建两个目标函数：1)系统总成本(包含建设成本、运输配送成本、运营管理成本)最小；2)配送中心的容量利用率最好。将每个投入使用的配送中心承担的配送量任务占其总容量的百分比为其容量利用率。投入使用的配送中心的最低容量利用率最大化作为决策目标2。而各候选配送中心的评估指标(表1)值很难用数学规划的方法进行量化表示，但其对设施选址又有重要影响。在此将各候选地址的评估结果作为参数，以最终选址方案的各配送中心的评估值均值最大化作为优化目标3。

要解决的问题是：如何确定配送中心的选址；如何确定供应点与选定配送中心之间的供应量；如何确定选定配送中心与所服务需求点之间的供应量；使得系统总成本最小、选定配送中心容量利用率最大、选定配送中心的评估均值最大。

2.2 符号定义

参数：

I为供应地数量，i=(1,2,…,I)；

J为需求地数量，j=(1,2,…,J)；

K为配送中心数量，k=(1,2,…,K)；

N为规划将要建设的配送中心的数量限制；

pi为供应点i的生产能力或容量限制；

pk为配送中心k的容量限制；

qj为需求地对产品的需求量；

lik为供应点i到配送中心k的距离；

lkj为配送中心k到需求地j的距离；

c1为供应点到配送中心之间的单位运量单位运距的平均运输成本；

c2为配送中心到需求点之间的单位运量单位运距的平均运输成本；

fk为配送中心k的建设成本；

ck为经配送中心k流转的产品的单位管理成本；

sk为候选地址的综合评估数值结果；

α为一较小数，确保分母不为零；

β为一极大数；

决策变量：

xik为供应点i为配送中心j的供货量；

ykj为配送中心k为需求地j的配送量；

zk为0-1变量，表示配送中心k建立与否。

2.3 确定需求下的多目标优化模型

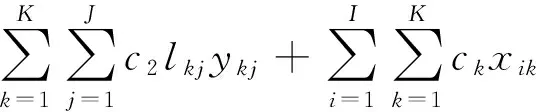
(10)

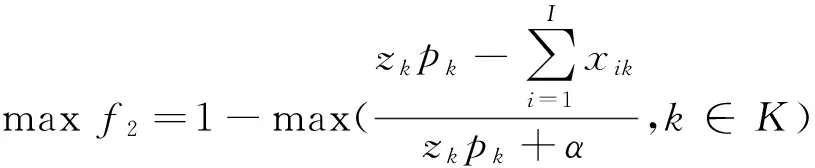
(11)

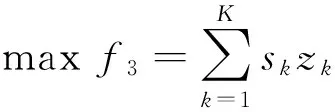
(12)

s.t.

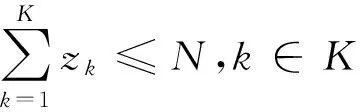
(13)

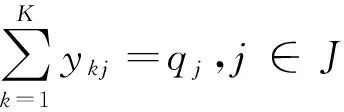
(14)

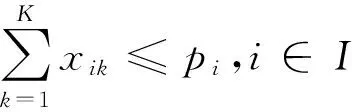
(15)

(16)

(17)

ykj≤βzk,k∈K,j∈J;

(18)

xkj≤βzk,k∈K,i∈I;

(19)

zk∈(0,1),k∈K。

(20)

式(10)为总成本目标函数，依次为建设成本、配送运输成本、供货运输成本、管理成本；式(11)为容量利用率目标函数，表示投入使用的所有配送中心中最低容量利用率最大化；式(12)为评估值目标函数，表示投入使用的配送中心评估值均值最大化。式(13)表示建设配送中心总数量小于N；式(14)表示需求点j的需求量被满足；式(15)为供应点的容量限制；式(16)为配送中心的容量限制；式(17)表示配送中心的进出流量相等；式(18)表示需求分配只建立在已建成的配送中心之上；式(19)表示供应只建立在已建成的配送中心之上；式(20)为0-1变量约束。

2.4 模糊需求下的模型构建

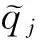
(21)

将需求量转化成模糊需求后，对模型中的需求量约束产生了影响，模型中的需求量约束变为：

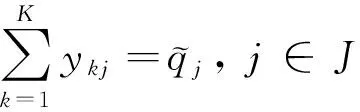
(22)

(23)

经过对模糊数的清晰化处理后，将原来含有模糊变量的约束式转化成两个清晰变量的不等式约束，就可以对其进行常规求解了。

3 算例分析

3.1 算例参数值

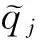
η=0.9。

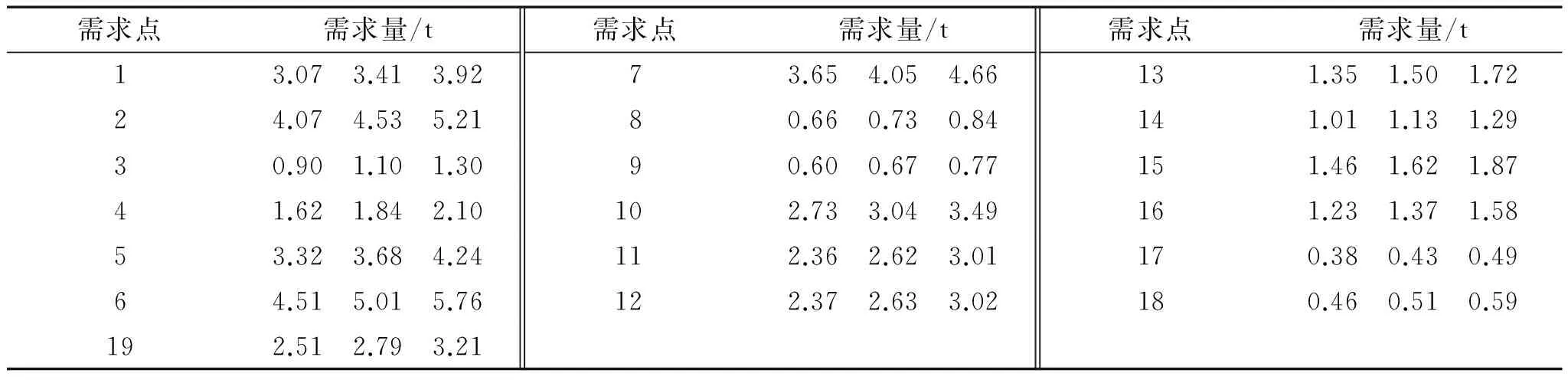
表2 各需求点的需求量统计

表3 候选配送中心相关参数估计

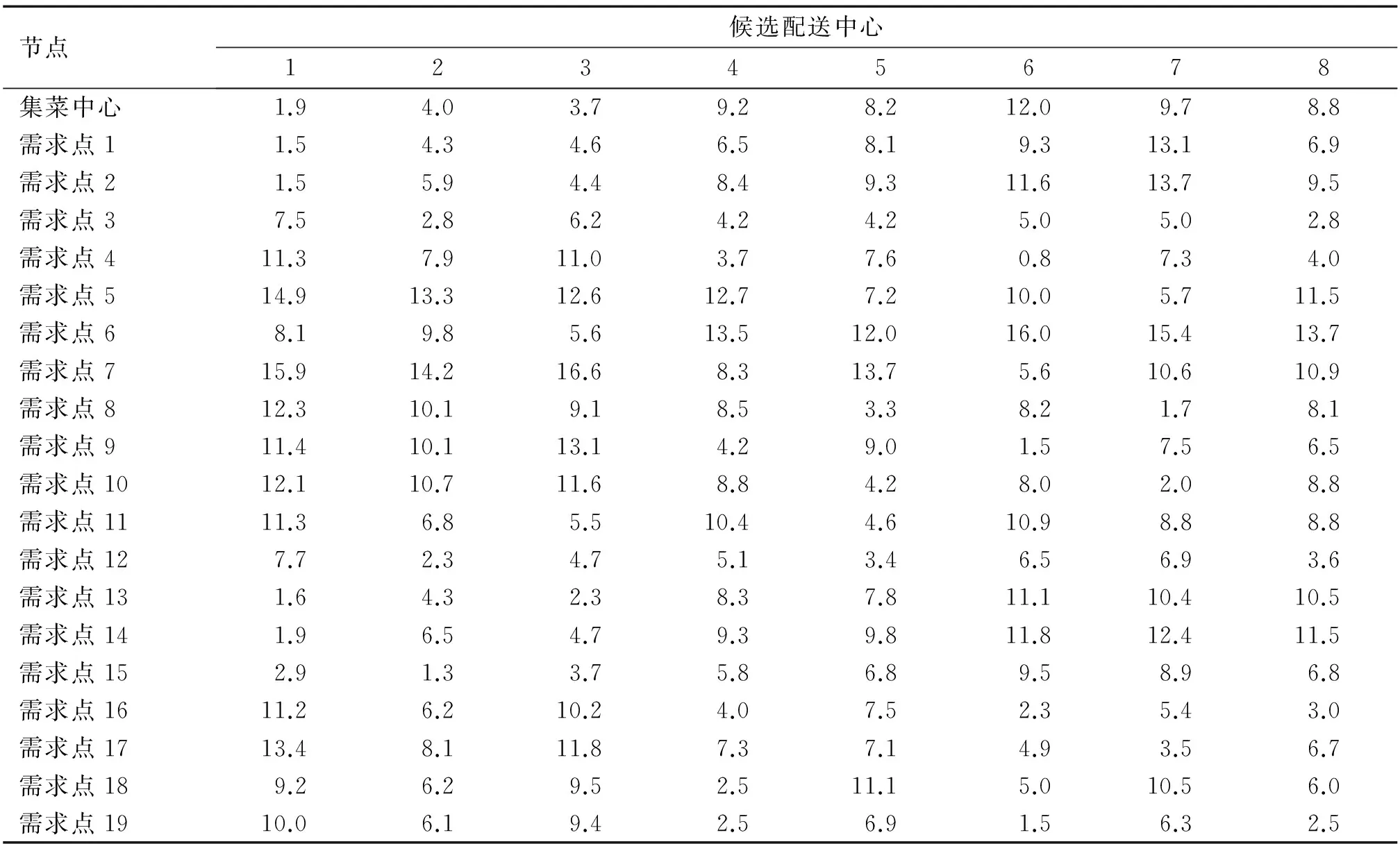
表4 各节点之间的距离

3.2 基于灰色聚类决策的候选地综合评估

指标权重基于AHP确定[19-20]。最终的权重信息分布为：

wB1-4-A=

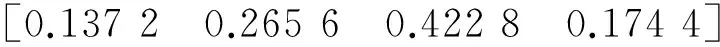
wC11-14-B1=

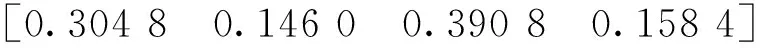
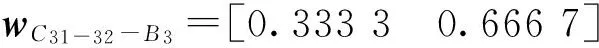
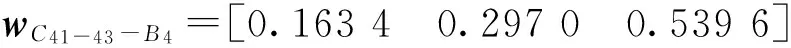
评估样本矩阵通过专家打分确定。邀请6位专家进行打分，打分越高表示在该指标下，候选地址越适合建立配送中心。将评分结果制成评估样本矩阵表。第1个候选配送中心评估样本矩阵如表5。

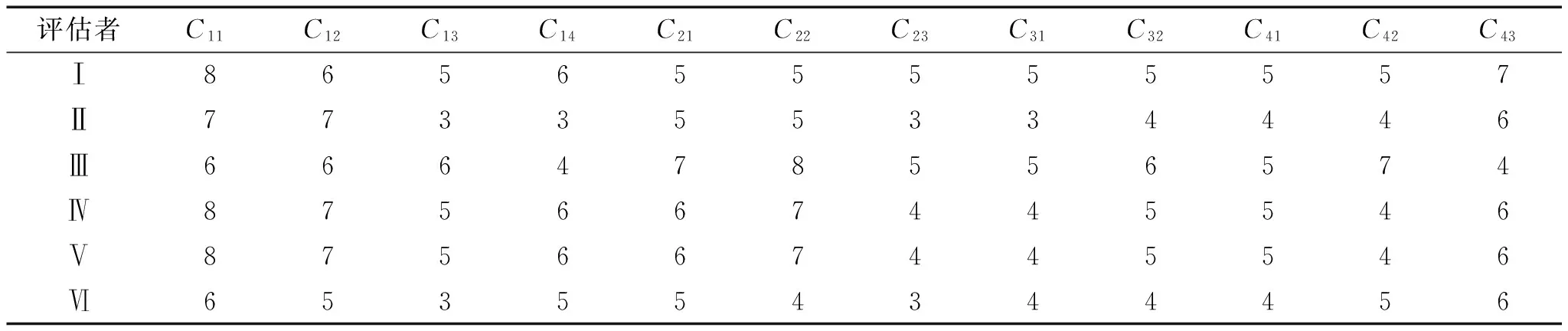
表5 评估样本矩阵(dij)

设置“优”、“良”、“中”、“差”4个评估灰类，即h=1,2,3,4，并分别设置白化权函数。

若h=1，设定灰数⊗∈(7,9,∞)，dij∈D，白化权函数为

(24)

若h=2，设定灰数⊗∈(5,7,9)，dij∈D，白化权函数为

(25)

若h=3，设定灰数⊗∈(3,5,7)，dij∈D，白化权函数为

(26)

若h=4，设定灰数⊗∈(0,3,5)，dij∈D，白化权函数为

(27)

按照1.4～1.7节所示步骤，进行候选地灰色聚类决策的综合评估，得到8个候选地的综合评估值依次为：6.645 2，6.399 2，6.482 5，7.134 8，5.944 1，5.716 5，4.972 6，6.430 7。

3.3 模糊多目标优化模型的求解

所建模型为一个多目标混合整数规划模型。在此，采用加权法将模型转化为单目标模型，再对其进行求解，具体的求解步骤描述如下。

1)统一量纲，对各目标进行规范化处理。由于各目标的量纲不一致,各目标之间的数量级相差太大，最终的单目标就失去意义。所以在进行求解时有必要进行无量纲处理。由于将多目标模型最终转化为最小化单目标优化模型，所以针对原目标中各个目标函数，采用如下的规范化处理方法[21]：

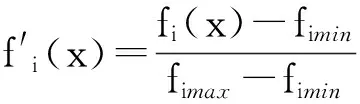
(28)

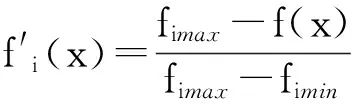
(29)

fimax、fimin分别为模型在单目标函数fi下的目标最大、最小值。式(28)为目标函数1的规范化处理方法，式(29)为目标2、3的规范化处理方法，结果如下：

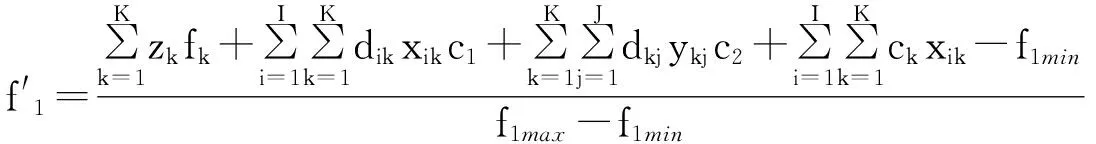
(30)

(31)

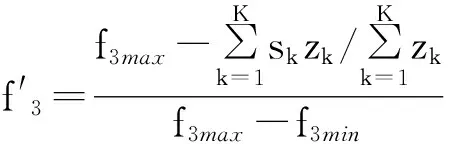
(32)

2)多目标转化为单目标。模型中的3个目标分别为成本最小、评估值最大、配送中心最小利用率最大，在经过规范化处理后，将多目标问题通过权重和法转化为单目标最小化问题。而各目标的权重的确定方法较为多样，本文采用最直接的主观赋权法，通过决策者偏好进行权重赋值。其中θ1,θ2,θ3为决策者的权重偏好，且有θ1+θ2+θ3=1。

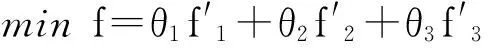
(33)

3)通过上述方法将多目标转化为单目标以后，整理算例数据就可以模型进行求解。

3.4 结果分析

采用lingo软件以上述步骤求解模型。首先计算出各单目标下的最小值和最大值(表6)。

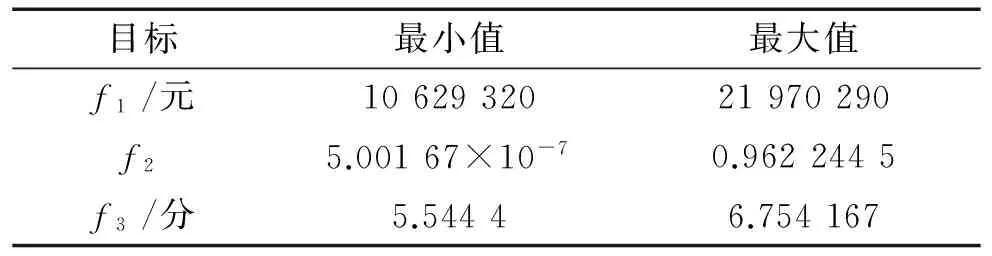
表6 各单个目标下的最小值和最大值

为分析不同目标对选址方案产生的影响，运用权重和法给出6组不同的权重值，将数据代入程序中，得出不同权重值下的选址分配方案及各目标函数值(表7)。各方案下配送中心需求量分配情况见表8。

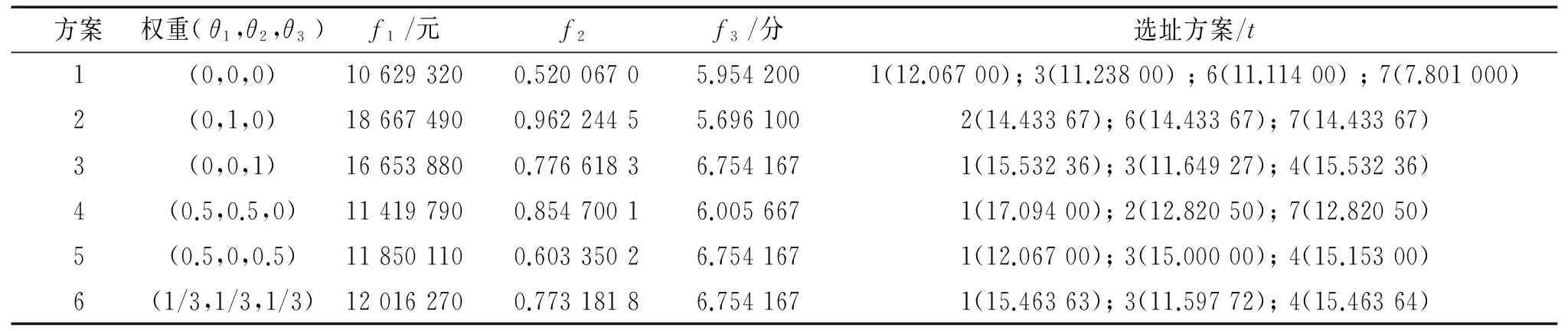
表7 不同权重系数下的选址方案

1)模糊需求下各点获得的需求略有浮动。

基于机会约束规划下的需求量并非定值，在成本目标和容量利用率目标下的需求量分配，会存在0～0.1的差距，且大部分的差值在0.05以下，但各需求点获得的需求量分配仍在其取值的上下限以内，并接近最可能值。

2)单目标下的优化方案。

(1)在追求成本目标下的选址方案为1、3、6、7；总成本10 629 320元；4个配送中心容量利用率分别为60.3%，74.9%，74.1%，52.0%；6、7号候选地址的评估值分别为5.7165、4.9726。

(2)在追求容量利用率目标下的选址方案为2、6、7；总成本18 667 490元；3个配送中心的容量利用率均为96.2%；6、7号候选地址评估值偏低。

(3)在追求评估值目标下的选址方案为1、3、4；总成本为16 653 880元；3个配送中心的容量利用率均为77.7%；1、3、4三个候选地址的评估值是最高的3个。

3)同时考虑两个目标的优化方案。

(1)在同时考虑成本目标和容量利用率目标时，选址方案为1、2、7；总成本为11 419 790元；3个配送中心的容量利用率均为85.5%。达到了成本优化和容量利用率优化的效果，但是由于缺乏评估值目标的优化，选中的7号候选地址的评估值较低，不太适宜建址。

(2)在同时考虑成本目标和评估值目标时，选址方案为1、3、4；总成本11 850 110；3个候选地址的评估值均值为6.754 167；1、4号配送中心的容量利用率为60.3%、75.8%。

4)3目标下的优化方案。

在3个目标权重都取1/3时，选址分配方案为1、3、4；此时的总成本为12 016 270元；3个配送中心的利用率均为77.3%；评估值均值为6.754 167，在该方案下，各目标函数值都得到了一定的调和，是比较满意的选址方案。

与仅考虑成本最小化方案相比，虽然同时考虑3个目标的方案在成本上有所增加，但在容量利用率和综合评估值上却得到了优化。根据不同的权重系数赋值，可以得出一系列解集供决策者参考。

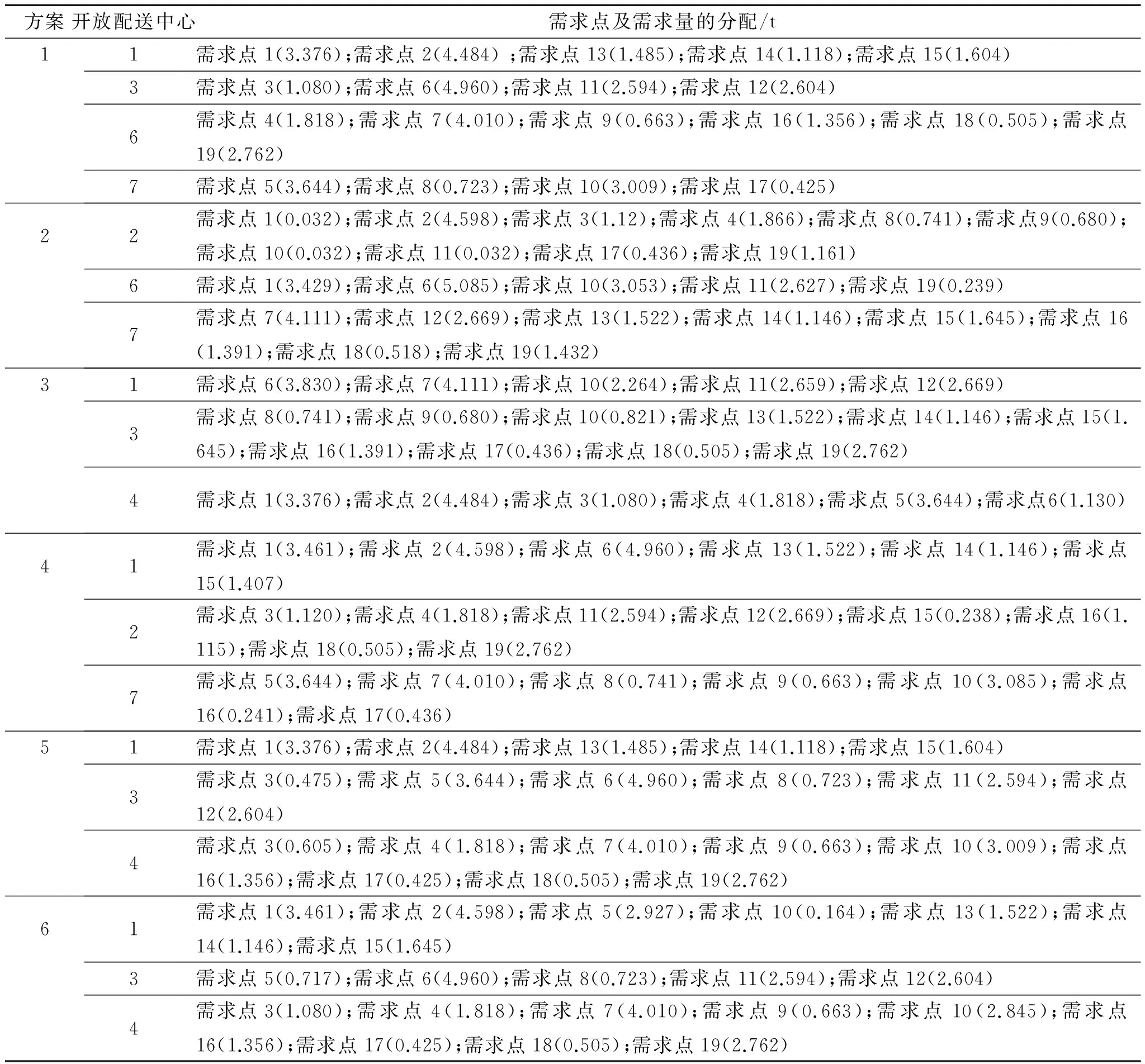
表8 方案1～6下各配送中心需求分配1)

1)需求点后括号内的数值表示需求分配量

4 结论

本文综合灰色聚类评估与多目标优化方法，研究了考虑模糊需求、供应点与配送中心容量限制的三级供应链系统配送中心选址优化问题。该问题被描述成一个3目标的非线性混合整数规划模型。采用机会约束规划对模糊需求进行清晰化处理，并应用目标加权的方法将问题转化为单目标问题。通过算例验证了所提模型的可行性。在实际工作中，可根据决策者权重偏好得出令人满意的结果，因而本文提出的集成模型具有一定的实用价值。

[1] YANG J, LEE H. An AHP decision model for facility location selection[J]. Facilities, 1997, 15(9/10): 241-254.

[3]ZHANG Y, HU X, LI Z. Distribution center location based on combining gravity method with fuzzy-AHP model[J]. Logistics Technology, 2009, 28(10): 56-58.

[4]GUTJAHR W J, DZUBUR N. Bi-objective bilevel optimization of distribution center locations considering user equilibria[J]. Transportation Research Part E: Logistics and Transportation Review, 2016, 85(1): 1-22.

[5]NEEMA M N, OHGAI A. Multi-objective location modeling of urban parks and open spaces: continuous optimization[J]. Computers, Environment and Urban Systems, 2010, 34(5): 359-376.

[6]AMIN S H, ZHANG G. A multi-objective facility location model for closed-loop supply chain network under uncertain demand and return[J]. Applied Mathematical Modelling, 2013, 37(6): 4165-4176.

[7]BADRI M A. Combining the analytic hierarchy process and goal programming for global facility location-allocation problem[J]. International Journal of Production Economics, 1999, 62(3): 237-248.

[8]LIU Nan, CHEN Yuangao, LI Yumin. Comprehensive decision making method for optimal location of logistics hubs[J].Journal of Southeast University(English Edition), 2007, 23(S1):71-75.

[9]莫海熙,郜振华,陈森发.基于AHP和目标规划的物流配送中心选址模型[J].公路交通科技, 2007(5):150-153.

MO Haixi, GAO Zhenhua, CHEN Senfa. Location model of distribution center based on analytic hierarchy process and goal programming[J]. Journal of Highway and Transportation Research and Development, 2007(5):150-153.

[10] 张华,何波,杨超.基于粗糙集和多目标规划的多物流配送中心选址[J].工业工程与管理, 2008, 13(2):69-73.

ZHANG Hua, HE Bo, YANG Chao. [J].Industrial Engineering and Management, 2008, 13(2):69-73.

[11]OZGEN D, GULSUN B. Combining possibilistic linear programming and fuzzy AHP for solving the multi-objective capacitated multi-facility location problem[J]. Information Sciences, 2014, 268(6):185-201.

[12]徐杰,郑凯,田源,等.物流中心选址的影响因素分析及案例[J].北方交通大学学报, 2001, 25(5):80-82.

XU Jie, ZHENG Kai, TIAN Yuan, et al. Research of logistics center location and case analysis[J]. Journal of Northern Jiaotong University, 2001, 25(5):80-82.

[13]王海军,黎卜豪,刘康康.应急救援下需求分配与网络配流研究[J].系统工程理论与实践, 2015, 35(6):1457-1464.

WANG Haijun, LI Buhao, LIU Kangkang. Demand allocation and network flow assignment under emergency rescue circumstance[J]. Systems Engineering—Theory & Practice, 2015, 35(6): 1457-1464.

[14]张晓楠,范厚明,李剑锋.B2C物流配送网络双目标模糊选址模型与算法[J].系统工程理论与实践, 2015, 35(5):1202-1213.

ZHANG Xiaonan, FAN Houming, LI Jianfeng. Bi-objective fuzzy location model and algorithm for the design of logistics distribution network in B2C e-commerce[J]. Systems Engineering—Theory & Practice, 2015, 35(5): 1202-1213.

[15]LIU B, IWAMURA K. Chance constrained programming with fuzzy parameters[J]. Fuzzy Sets & Systems, 1998, 94(2):227-237.

[16]刘宝碇,赵瑞清.随机规划与模糊规划[M].2版.北京：清华大学出版社, 2001 :164-172.

[17]周蕾.物流规划中的双层优化模型与方法研究[D].天津：天津大学, 2007.

ZHOU Lei. Research on bi-level model and method in logistics programming[D]. Tianjin: Tianjin University, 2007.

[18]SPAFFARI-NASAB N, AHARI S G, SPAFFARI M. A hybrid simulated annealing based heuristic for solving the location-routing problem with fuzzy demands[J].Scientia Iranica, 2013, 20(3):919-930.

[19]何方珍.物流园区选址决策研究及应用[D].重庆：重庆大学, 2006.

HE Fangzhen. Research and application on logistics park location decision[J]. Chongqing: Chongqing University, 2006.

[20]任永昌,刑涛,赵国强.物流配送中心选址方案模糊决策分析[J].辽宁工程技术大学学报(自然科学版), 2010, 29(3):517-520.

REN Yongchang, XING Tao, ZHAO Guoqiang. Fuzzy decision analysis on logistics distribution center location plan[J]. Journal of Liaoning Technical University(Natural Science), 2010, 29(3):517-520.

[21]李丹.钢铁销售物流网络节点选址研究与应用[D].重庆：重庆大学, 2014.

LI Dan. Research and application on location of steel distribution logistics center[D]. Chongqing: Chongqing University, 2014.

A Fuzzy Multi-objective Optimization Model for Distribution Center Location Based on Grey Clustering Evaluation

LI Zhi1, JIANG Zhou2, ZHOU Yufeng1

(1. Chongqing Engineering Technology Research Center for Information Management in Development,Chongqing Technology and Business University, Chongqing 400067, China; 2. Chongqing Key Laboratory of Electronic Commerce & Supply Chain System, Chongqing Technology and Business University, Chongqing 400067, China)

A logistics system has distribution centers as its key nodes, and the rationality of distribution centers location decision is of great value. The location of multi-distribution centers is studied integrating multi-attribute decision making method and optimization method. Firstly, the candidate locations are evaluated based on grey clustering decision. Then, three objective functions are considered as follows, to minimize the total logistics cost, to maximize the capacity utilization and mean evaluating scores of open distribution centers. Besides, a distribution center location model in three echelon supply chain system is built considering fuzzy demands and capacity constraints. This model is depicted as a mixed integer nonlinear programming model. Using chance constrained programming to clear the fuzzy demand, the problem is transformed into a single objective problem based on target weighting. Lastly, a numerical example is given to verify the feasibility of the proposed model. In reliability, satisfactory results can be obtained according to the weight preference of the decision makers.

distribution center; location; grey clustering evaluation; multi-objective optimization model

2016- 05- 02

教育部人文社会科学研究资助项目(15XJC630009); 重庆市教委科学技术研究资助项目(KJ1500603); 重庆工商大学科研启动经费资助项目(2015-56-10); 重庆工商大学校内科研资助项目(670101548);重庆市发展信息管理工程技术研究中心开放基金资助项目(gczxkf201602)

李志(1965-)，男，重庆市人，教授，硕士，主要研究方向为物流系统规划、物流信息化与供应链管理.

10.3969/j.issn.1007- 7375.2016.05.004

F272

A

1007-7375(2016)05- 0024- 09