机器学习算法在焊接领域中的应用

李 驰，李广军

（1.四川大学 锦城学院计算机科学与软件工程系，成都611731；2.江苏理工学院 汽车与交通工程学院，江苏 常州213001）

机器学习算法在焊接领域中的应用

李 驰1，李广军2

（1.四川大学 锦城学院计算机科学与软件工程系，成都611731；2.江苏理工学院 汽车与交通工程学院，江苏 常州213001）

针对机器学习算法已经渗透到了焊接领域的情况，在对近年来焊接领域相关文献深入研究分析的基础上，重点阐述了在焊接领域运用较多的神经网络、支持向量机和遗传算法。分析总结了机器学习算法在焊接领域的应用方式，包括标准应用、改进应用和交叉混合应用。同时也介绍了机器学习算法在建模预测与参数优化、路径规划与焊接顺序、过程控制与质量监测和缺陷识别与分类判定方面的应用情况。对机器学习算法在焊接领域的未来发展进行了展望。

焊接；机器学习算法；人工神经网络；支持向量机；遗传算法

焊接作为一种重要的制造技术，被广泛应用于工业生产中。焊接过程属于典型的不确定性非线性系统过程，在这个过程中会发生复杂的物理化学反应，且该过程受到各种因素的影响，因此很难凭经验或者简单的数学公式建立精确的模型。而机器学习，作为人工智能的一个核心组成部分，近年来有了长足的发展，并在焊接领域中有非常活跃的应用。广义的机器学习算法包括神经网络、随机退火算法、遗传算法、支持向量机以及各种群集算法等。

1 焊接领域中常见的机器学习算法

1.1 神经网络

神经网络实际上是人工神经网络（artificial neural network，ANN）的简称，是一种在生物网络的启示下建立的数据处理模型。神经网络由大量的人工神经元相互连接进行计算，根据外界的信息改变自身的结构，主要通过调整神经元之间的权值来对输入的数据建模，最终具备解决实际问题的能力[1]。

神经网络系统中应用最多的当属BP神经网络。它的基本思想是学习过程由信号的正向传播与误差的反向传播两个过程构成。正向传播时，输入样本从输入层传入，经过各隐层处理后，传向输出层。当实际输出与期望值有误差时，转向误差的反向传播阶段。误差反传将误差通过隐层向输入层逐层反传，并在各层分摊误差，这些误差即作为修正各单元权值的依据[2]。以上过程将循环执行，直到满足某个收敛条件。

下面简单介绍一下典型的三层BP神经网络的算法，三层包括了输入层、隐层和输出层，如图1所示。用电火花加工方法在高强铝合金试块底面制作了不同深度的人工窄槽来模拟底面开口裂纹。B扫描图像的获取在超声C扫描检测系统上进行，系统采样频率为100 MHz……。试验所用试块及其扫描方式如图1所示。

图1 三层BP神经网络

其中，X=（x0，x1，...，xi，...，xn）T为输入向量；Y=（y0，y1，...yj，...，ym）T为隐层输出向量；O=（o1，o2，...，ok，...，ol）T为输出层输出向量； d=（d1，d2，...，dk，...，dl）T为期望输出向量； V 和 W 分别为隐层和输出层的权值向量。

对于输出层，有

对于隐层，有

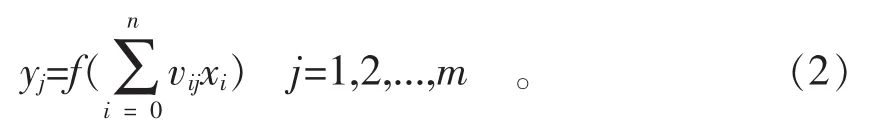
变换函数 f（x）均为单极性Sigmoid函数。

网络输出与期望值的误差可以定义为

由公式可以看出，此误差是各层权值wjk、vij的函数，因此调整权值可以改变误差。为使此误差不断减小，应使权值调整量与误差的梯度下降成正比。根据这个思路，对BP算法推导（详细过程略），得出以下结论

从公式（1）~公式（5）可以看出，每一层权值调整量都等于学习率η、局部梯度δk或者δj和上一层输出信号yj或者xi三者的乘积。同时，每一层局部梯度的计算都要用到上一步计算的结果，即前一层的局部梯度是后一层局部梯度的加权和。

1.2 支持向量机

支持向量机方法是建立在统计学习理论的VC维理论和结构风险（包括经验风险和置信风险）最小原理基础上的，能在有限的样本信息基础上，尽量提高求解实际问题时的泛化能力[2]。

从线性可分模式分类来看，支持向量机的主要思想可以如图2所示。

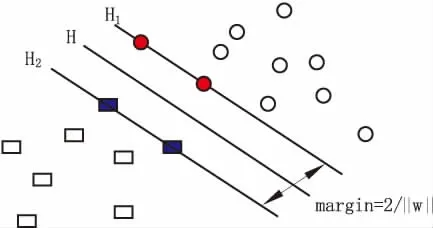
图2 线性可分模式下SVM的最优分类

它试图建立一个最优决策超平面（图中H平面），不仅能将两类正确分开，而且使得这个分开的margin最大化。设线性可分的样本集合（xi，yi），i=1，2，…，n，x∈Rd，y∈{+1,-1}。其中x为输入向量，y为期望输出值。用于分类的超平面方程为wx+b=0，其中w为权值向量，b为偏置。经过数学推导分类间隔的计算公式为margin=2/||w||，这样求解最大间隔的问题转化为求||w||的最小值，结合一定的约束条件，最后问题转化为数学表达式，其中约束条件为 s.tyi（wxi+b）-1≥0i=1，2，…，l。

这是一个二次凸规划问题，代价函数是凸的，且约束条件是线性的，可以使用Lagrange系数方法来解决。引入Lagrange函数为

式中：α≥0，i=1，2，…，k称为Lagrange系数。

最后经过推导（详细过程略），可以得到最优分类判别函数，即

式中，α*和b*—确定最优化分超平面的参数;

—两个向量的内积。

对于线性不可分问题通常有两种解决方式。如果仍然要得到完全的正确分类（训练错误率为0），可以通过坐标转换，将问题从低维映射到高维，即分类函数变为

这个变换映射过程是很复杂的，我们并不关心这个复杂的过程，只要得到这个变换后的内积结果即可，核函数即可得到这样的结果，令K（xi，x）=<φ（xi）·φ（x）>。 常用的核函数有线性核函数、多项式核函数和径向基核函数等。

如果即使变换到很高的维度仍然不能线性可分或者故意允许一定的容错能力的话，可以采用另一种解决线性不可分的方式，即引入松弛变量。这样，标准的问题表达就从公式（6）变为min，其约束条件为 s.t yi（wxi+b）-1+ξi≥0i=1，2，…，l。

其中ξ为松弛变量,它表明对应点离群的程度，即被错分的严重程度；C>0代表惩罚因子，值越大惩罚越严重。

1.3 遗传算法

遗传算法是一种模仿自然界生物进化机制发展起来的随机全局搜索和优化方法。它能在搜索过程中自动获取积累有关搜索空间的知识，并自适应的控制搜索过程以求得最优解。

遗传算法的步骤：①染色体编码。标准遗传算法对初始群体中各个个体的基因采用固定长度的二进制符号串来编码；②个体适应度的检测评估。算法将适应度函数作为评判个体优劣的唯一标准，它与目标函数有关，必须为非负数；③遗传算子操作。这个步骤包括三个算子操作，分别是选择、交叉和变异。①选择运算。最常见的选择算子是轮盘赌，它规定个体能被选择保留的概率大小直接由其对应的适应度函数值决定；②交叉运算。最常见的交叉算子为单点交叉，即任意挑选经过选择操作后种群中两个个体作为交叉对象，随机产生一个交叉点位置，在该位置两个个体互换部分基因码，形成两个新个体；③变异运算。最常见的变异算子为基本变异。随机选取一个位置上的基因进行小概率的翻转，即0变1或者1变0。这三个子步骤将一直循环迭代，直到满足某个收敛条件才停止。

2 机器学习算法在焊接领域中的应用方式

2.1 算法的独立应用

本研究把机器学习算法的应用分为标准算法的应用和改进算法的应用。标准算法最早由前人提出，虽然年代久远，现在直接使用的场合并不多，但毕竟算法经典，简单直接，故仍有一些直接应用实例。

改进算法是经过多年的应用，标准算法逐渐暴露出这样那样的缺陷，后人对其进行的不同角度的改进和优化。例如，文献[3]中对传统的BP算法进行了三方面的改进。包括在权值更新阶段引入动量因子，使得系统有一定的惯性，算法有了一定的抗震荡能力，并加快收敛。通过检查权值和阈值修正与误差的关系来动态的设置自适应学习率，提高算法的性能和稳定性。采用梯度下降和拟牛顿法相结合的LM算法简化计算，加快收敛。文献[4]针对经典遗传算法不能保证取得全局最优，收敛速度不理想的缺陷，提出了一种基因植入遗传算法，即当种群进化到快要陷入局部收敛时，将每一代保存的最优基因和以一定比例随机抽取的历史基因形成的基因库与目前种群中的部分基因替换，从而产生激活状态，扩大搜索寻优的范围。实验表明，将其用于焊接机器人的规划取得了满意的效果。文献[5]采用了一种改进的SVM算法来在线监测船舶水下焊接质量，与经典SVM算法不同的是这种最小二乘支持向量机算法将算法中的不等式约束改为了等式约束，兼顾模型的复杂性与学习能力，比经典SVM预测性能更好，更容易获得全局最优解。

2.2 算法的交叉综合应用

各种机器学习算法有其自身的优缺点，有时将几种算法结合使用，扬长避短，更能够发挥综合应用的效果。文献[6]将遗传算法与神经网络结合来优化焊接接头力学性能预测模型。该算法先采用遗传算法的寻优方式找出BP神经网络的最佳初始权值和阈值，再代入BP神经网络进行训练和预测，以避免单纯BP神经网络算法的初始权值随机选取造成的较大误差。文献[7]采用一种将遗传算法和随机神经网络中的模拟退火算法相结合的算法来规划弧焊机器人的焊接路径。这种算法既具有遗传算法的全局性和并行性，又具有模拟退火算法的局部搜索能力退火特征。它在遗传算法的群体选择步骤中增加了一个按照一定概率随机搜索领域的环节，这正是模拟退火的显著特征，从而使选择范围比单纯的遗传算法更大。

3 机器学习算法在焊接中的应用领域

3.1 建模预测与参数优化

焊接过程属于典型的非线性过程，由于工艺复杂，涉及的参数较多，很难用直接的数学公式来映射其输入与输出。而机器学习中的各种优化算法可以提供一套理论来建立这种映射模型，从而根据历史经验的训练样本数据来提前预测各种不同焊接条件和焊接工艺对焊接性能的影响。文献[8]广泛收集整理了企业第一线的焊接数据，并建立起了相关数据库。应用遗传算法优化BP神经网络，建立了焊接接头力学性能预测模型，实现了根据材料成分、焊接工艺和温度参数较为准确的预测包括抗拉强度、屈服强度、断后伸长率以及断面收缩率等在内的力学性能指标的目的。文献[9]针对2205双相不锈钢，分别建立了焊接应力和收缩变形的支持向量机回归预测模型，较好的模拟了焊接残余应力和变形与板厚、焊接电流、电弧电压、焊接速度等工艺参数之间的非线性关系，并与传统的逐步回归方法进行了比较，结果表明，支持向量机回归的预测精度和泛化能力更好。文献[10]建立了基于RBF径向基神经网络焊接工艺参数选择模型，实现了从输入的焊接条件（材料种类、母材厚度、坡口形式和焊接位置）到输出的焊接工艺参数（焊丝直径、焊接电流、电弧电压和焊接速度）的非线性映射。并在建模过程中对样本数据采取了对数变换的预处理方式。结果表明其预测误差小于1e-9%，满足生产实际需要。文献[11]为了找到最小焊接变形对应的焊接能量（焊接电流和电压）和焊接速度工艺参数的最优组合，采用MATLAB软件实现遗传算法，结合非线性仿真软件Mac中的有限元方法进行每组参数组合的焊接过程热力耦合分析，取得了令人满意的结果。

3.2 路径规划与焊接顺序

路径规划与焊接顺序从本质上来说是一个组合优化问题。也可以把它抽象为排列组合问题、货郎担问题或者旅行商问题。由于这类问题的组合方式数量呈指数型增长，传统的线性规划、动态规划和分枝界定等精确算法并不适用，而机器学习算法中的很多仿生算法比较适合解决这类问题，遗传算法就是这些算法中的一个典型代表。但是由于焊接工程本身的复杂性，实际中的运用不能简单的等同于一个纯粹的数学问题，有时会根据一些实际情况加入约束等。文献 [12]为了找到箱型梁最小焊接变形对应的焊接顺序，采用了遗传算法，以N进制不重复数字编码，将焊接变形设为适应度函数，并结合热-机耦合弹塑性非线性有限元模型来求解焊接变形量。实验表明这种方法不仅有效而且也可以推广到其他焊接结构。文献[13]为了找出轿车白车身机器人焊接的最短路径，将该问题转化为一个带约束的货郎担问题，采用遗传算法，同时将约束融于局部有向图中，适应度函数选定为最短焊接时间，经过MATLAB语言编程仿真表明通过遗传算法结合图论的方法取得的焊接路径顺序具有较优的结果。文献[14]通过生成船舶装配树结构中的各种装配计划方案，利用遗传算法和产品模型来进行船舶装配树结构的优化。考虑到实际的一些不可行的组合方式，在遗传算法的适应度函数中引入惩罚因子，采用联赛选择法和两点交叉算子，最终得到一个优化的船舶分段搭载系统。

3.3 过程控制与质量监测

焊接的质量和结果取决于焊接的过程，所以必须对焊接的整个过程实时监测并进行有效的控制。很多机器学习的优化算法可以很好的运用到焊接的过程控制与质量监测中，并已经取得了不错的结果。这些算法结合自动控制领域中的传感器、摄像头等反馈设备和控制器，可以形成一个具有智能反馈功能的系统，实现对焊接过程的有效控制和监测。文献[15]设计了一种基于遗传算法的参数整定PID控制器，并将其应用于旋转TIG焊接系统中。该系统将比例系数、积分系数和微分系数编码，将焊缝位置误差通过电弧传感器实时的反馈回来控制下一次的输入，从而改善了系统的实时跟踪性能，提高了焊接质量。文献[16]针对激光焊接过程，利用支持向量机的辨识预测控制方法来建模和控制。系统根据辨识模型预测未来的输出状态，经反馈校正后与参考输入做比较，对目标函数进行优化，进而起到控制作用，完成整个控制循环。文献[5]建立了一个基于最小二乘支持向量机的预测模型对船舶水下焊接质量进行了在线监测。模型通过各种焊接工艺参数来在线预测焊接熔深，再利用模糊逻辑推断出焊接质量级别，并对有缺陷的质量级别进行实时显示和报警。

3.4 缺陷识别与分类判定

焊接工艺的复杂性导致不可避免的会出现焊接缺陷。由于焊接缺陷的种类多，界限模糊，数量不平衡，对焊接质量的影响程度不同，要求我们不但要识别是否有焊接缺陷，还要识别出是哪一种类别的焊接缺陷。文献[17]针对水压试验条件下API SPEC 5L X70管线钢，利用BP神经网络技术，将铁磁性材料金属磁记忆信号的小波包能量在8个频带的能量分布作为模型特征向量输入，可以较好的实现对焊缝中有无焊接裂纹的分类识别，总体识别率令人满意。文献[18]采用一种改进的遗传算法——量子遗传算法来处理从发射台骨架试验模型中获取的模态参数。方案中以有限元模型焊接结点单元组弹性模量的降低来模拟焊缝损伤，以实测模态和计算模态之间的误差建立了一个带约束边界的非线性最小二乘目标函数，将损伤识别问题转化为了优化问题。实验表明在给定焊缝损伤工况下，对损伤的位置和程度都能很好的识别。文献[19]提出了一种广义加权支持向量机焊接缺陷分类算法。该算法通过在传统的SVM算法中引入一个由样本平衡权重、样本重要性权重和类别重要性权重的乘积构成的加权系数，不仅使得对焊接缺陷样本数量不平衡时的分类总体精度有所改善，而且对样本数量少、重要缺陷的检查精度有明显提高。文献[20]将支持向量机应用到了射线检测焊接图像缺陷识别中。方案根据焊接缺陷图像的8个特征参数作为训练识别的样本，将SVM的两类分类推广到一对一模式的多类识别，完成了6个类别的焊接缺陷分类，取得了比较准确的结果。

4 未来发展展望

（1）算法本身的改进和算法的交叉综合应用。这在本研究的2.1和2.2中已经详细说明。

（2）算法的适用性选择。机器学习涉及的算法很多，每种算法都有其自身的优缺点及其对应的适用场合，很难说哪种算法一定好或者不好。BP神经网络能实现一个从输入到输出的映射功能，它具有实现任何复杂非线性映射的功能，同时也具有自学习、泛化和容错能力，这使得它特别适合于求解内部机制复杂的问题。但是，它也具有一个明显的缺点就是容易陷入局部极值。遗传算法非常适合用来求解最优化问题的。如可以将实际工程中的组合问题，规划问题的优化求解转化为求函数的最大、最小值问题。但遗传算法也面临容易发生早熟，适应度函数、初始种群规模、交叉概率、变异概率等参数不好确定的问题。SVM算法比较适合用来做分类和回归分析。分类不仅局限于两类，也可以推广到多类分类。回归分析可以实现类似BP神经网络的函数拟合功能，但由于具有全局最优，且所需样本数量较少，所以通常比BP神经网络的泛化能力更强。当然它也存在核函数和参数选取困难，训练时间较长的缺点。

（3）其他机器学习算法。在焊接领域除了前面介绍的三种运用最多的机器学习算法之外，其实还有一些优化算法也使用较多，比较典型的就是一类基于仿生学的群集算法。例如，文献[21]采用模仿鸟类觅食方式的粒子群算法对焊接企业车间的调度问题进行了研究。文献[22]采用模仿蚂蚁觅食方式的蚁群算法来解决焊接机器人路径规划问题。文献[23]通过模仿鱼类生活方式的鱼群算法与最小二乘支持向量机结合来优化摩擦焊接工艺参数。文献[24]将模仿蜜蜂生活方式的蜂群算法运用到了双机器人焊接路径的规划中，取得了较好的近似解。

（4）大数据时代的焊接历史数据收集。在大数据时代背景之下，企业在焊接过程和结果中保存的焊接状态、参数等数据对企业来说是一笔宝贵的财富。机器学习中的很多算法对数据量的多少和准确性都有一定的依赖。例如BP神经网络系统的样本输入输出数据过少，会直接影响到其预测建模的准确性。又如SVM算法尽管适用于小样本情况，但是这里小样本是相对问题规模的小样本，未必是绝对意义上的小样本。很多组合优化问题的组合方式的数量往往巨大，尽管可以通过诸如有限元分析的方式加以模拟，但是毕竟存在误差不及真实的实验数据准确。针对像BP神经网络系统、SVM算法这些有导师（有监督）学习算法，尤其需要事先标记输出值或者类别，所以已有的历史样本数据就格外的重要。企业如能在平时将各种焊接数据收集并保存下来，形成历史大数据，必将对今后的机器学习算法优化焊接工作带来便利。

[1]陈明.MATLAB神经网络原理与实例精解[M].北京：清华大学出版社，2013.

[2]韩力群.人工神经网络教程[M].北京：北京邮电大学出版社，2006：58，200.

[3]贾剑平，徐坤刚，李志刚.改进型BP网络在优化焊接工艺参数中的应用[J].热加工工艺，2008,37(21)：98-100.

[4]何谷慧，阎保定，孙立功，等.基因植入遗传算法在焊接机器人序列规划中的应用[J].河南科技大学学报（自然科学版），2008,29（5）：33-35.

[5]张为民，钟碧良.基于最小二乘支持向量机的船舶水下焊接质量在线监测[J].中国造船，2009，50（1）：117-120.

[6]董志波，魏艳红，占小红，等.遗传算法与神经网络结合优化焊接接头力学性能预测模型[J].焊接学报，2007,28（12）：69-72.

[7]陈志翔，殷树言，卢振洋.基于遗传模拟退火算法的弧焊机器人系统协调路径规划[J].机械工程学报，2005,41（2）：194-198.

[8]刘立鹏，王伟，董培欣，等.基于遗传神经网络的焊接接头力学性能预测系统[J].焊接学报，2011,32（7）：105-108.

[9]王智祥,王正伦.2205双相不锈钢焊接应力与变形的SVM 回归预测研究[J].船舶工程，2010,32（1）：74-78.

[10]彭泽军.基于RBF网络的MIG焊焊接工艺参数选择模型[J].焊接技术，2014,43（6）：35-39.

[11]冯超，韩俊杰，张红伟，等.基于Marc和遗传算法的焊接工艺参数优化[J].北京交通大学学报，2012,36(4)：149-152.

[12]崔晓芳，马君，赵海燕，等.基于遗传算法的箱型结构焊接顺序优化[J].焊接学报，2006,27（8）：5-8.

[13]张春伟，刘海江，姜冬冬.基于遗传算法的白车身机器人焊接路径规划[J].同济大学学报（自然科学版），2011,39（4）：576-580.

[14]姚竞争，韩端锋，苗玉刚.基于焊接速度的遗传算法在装配中的应用[J].焊接学报，2011,32（6）：89-92.

[15]贾剑平，刘云龙，金伟，等.基于遗传算法的位置PID控制器在旋转TIG焊接系统中的应用[J].焊接技术，2012,41（11）：37-39,67.

[16]邹伟，刘玉生.基于支持向量机的激光焊接过程辨识与控制[J].计算机仿真，2008,25（12）：114-117.

[17]邸新杰，李午申，白世武，等.焊接裂纹金属磁记忆信号的神经网络识别[J].焊接学报，2008,29（3）：13-16.

[18]王天辉，马立元，李世龙，等.基于量子遗传算法的钢管焊接结构焊缝损伤识别[J].海军工程大学学报，2012,24（6）：89-94.

[19]张晓光，肖兴明，任世锦，等.基于广义加权支持向量机的焊接缺陷分类方法[J].华东理工大学学报(自然科学版)，2005,31（5）：644-648.

[20]刘元祥，张晓光，高顶.基于支持向量机的射线检测焊接图像中缺陷识别[J].煤矿机械，2006,27（5）：773-776.

[21]樊坤，张人千，夏国平.随机双目标焊接车间调度建模与仿真[J].系统仿真学报，2009,21（13）：3096-3099.

[22]王家海，王毅.基于蚁群算法的白车身焊接机器人路径优化研究[J].制造业自动化，2008,30（5）：16-18.

[23]舒服华.基于LSSVM和AFSA的摩擦焊接工艺参数优化[J].焊接学报，2008,29（12）：104-108.

[24]王郑拓，冯振礼，叶国云，等.基于人工蜂群算法的双机器人路径规划分析[J].焊接学报，2015,36（2）：97-100.

Application of Machine Learning Algorithm in Welding Field

LI Chi1,LI Guangjun2
（1.Department of Computer Science and Software Engineering of Jincheng College,Sichuan University,Chengdu 611731,China;2.School of Automobile and Traffic Engineering,Jiangsu University of Technology,Changzhou 213001,Jiangsu,China）

The machine learning algorithm penetrated in welding field,based on deep analysis on the relevant literature in welding field in recent years,it emphatically expounded artificial neural network,support vector machine and genetic algorithm which are widely applied in the welding field.Analyzed and summarized the application mode of machine learning algorithm in the welding field,including standard application,improvement application and cross mixed application.And it also introduced the application of machine learning algorithm in the aspects of modeling prediction and parameter optimization,path planning and welding sequence,process control and quality monitoring,defect recognition and classification criteria.It also carried out future development outlook for machine learning algorithm in the welding field.

welding;machine learning algorithm;artificial neural network;support vector machines;genetic algorithm

TG409 文献标志码：B DOI:10.19291/j.cnki.1001-3938.2016.05.005

李 驰（1974—），男，四川成都人，硕士，讲师，主要研究方向为智能信息处理，机器学习，数据挖掘等。

2016-01-08

罗 刚