基于铸体薄片的致密岩心孔隙结构多重分形特征研究

李润泽，王长江，李 伟，栾东肖，韩军铮，崔海标，刘运泽 ，刘家雄

(1.青海油田 采气一厂，青海 格尔木 816000；2.中国石油集团测井有限公司 油气评价中心，陕西 西安 710077；3.中海油研究总院，北京 100027 ；4.华北油田公司第一采油厂 地质研究所，河北 任丘 062552；5.长庆油田分公司 第五采气厂，内蒙古 乌审旗 017300 ；6.大庆钻探地质录井一公司，黑龙江 大庆163000；7.中国石油大学(华东)地球科学与技术学院，山东 青岛 266580)



基于铸体薄片的致密岩心孔隙结构多重分形特征研究

李润泽1，王长江2，李 伟1，栾东肖3，韩军铮4，崔海标5，刘运泽6，刘家雄7

(1.青海油田 采气一厂，青海 格尔木 816000；2.中国石油集团测井有限公司 油气评价中心，陕西 西安 710077；3.中海油研究总院，北京 100027 ；4.华北油田公司第一采油厂 地质研究所，河北 任丘 062552；5.长庆油田分公司 第五采气厂，内蒙古 乌审旗 017300 ；6.大庆钻探地质录井一公司，黑龙江 大庆163000；7.中国石油大学(华东)地球科学与技术学院，山东 青岛 266580)

基于压汞和核磁共振实验进行了致密岩心孔隙结构分类，提取了不同孔隙结构的铸体薄片并应用PSO多阈值分割算法得到孔隙-骨架二值图。结合孔隙结构的多重分形理论计算了不同孔隙结构的多重分形维数及多重分形谱,分析了多重分形维数与饱和中值压力、平均孔喉半径和核磁T2几何平均值的关系。研究表明：基于多重分维表征方法与压汞、核磁共振等实验具有一致性，不同孔隙结构岩石的多重分形特征各异，物性越差、孔隙结构越复杂，多重分形维数越大；多重分形维数与饱和中值压力成正比，与平均孔喉半径和核磁T2几何平均值成反比；Dmin与孔隙结构类型及其他孔隙结构表征参数的相关性最强，在缺乏压汞、核磁等实验数据时，基于铸体薄片的多重分形维数为致密岩石孔隙结构的定量表征提供了有利依据。

致密岩石；孔隙结构；多重分形特征；铸体薄片；PSO分割

李润泽，王长江，李伟,等.基于铸体薄片的致密岩心孔隙结构多重分形特征研究[J].西安石油大学学报(自然科学版)，2016，31(6)：66-71，86.

LI Runze,WANG Changjiang,LI Wei,et al.Multifractal properties of tight rock pore structure based on thin section [J].Journal of Xi'an Shiyou University (Natural Science Edition),2016,31(6): 66-71，86.

引 言

储集空间及孔隙结构是影响储层产能的重要因素，也是测井评价的重要内容。相关研究是致密油气、页岩气等非常规能源勘探开发中的重要问题。通过实验得到定性、定量参数并根据“岩心刻度测井”建立孔隙结构参数或类型与测井响应的关系，实现基于测井资料的孔隙结构评价是国内外测井专家的主要研究方法。孔隙结构分析从实验手段上可分为铸体薄片、扫描电镜、毛管压力、等温吸附、核磁共振等；从分析方法上可分为拓扑参数评价、分形特征描述、统计规律表征等。

分形几何是一种非线性科学，揭示了复杂非线性系统中有序和无序、确定性和随机性的统一，在孔隙结构表征中具有独特优势。国内外学者已开展了大量的研究[1-7]，并探讨了分形维数与孔隙结构及岩石物理响应等关系[8-10]。针对单重分形的局限性[11-16]，部分学者又开展了多重分维的研究[17-21]，在地学、土壤学和材料学中取得了一定的应用效果。在孔隙结构多重分形方面，Gutierrez等分别开展了基于压汞曲线、X-CT、扫描电镜等资料的研究，分析了不同孔隙结构的多重分形特征及变化规律[22-27]。

与X-CT、扫描电镜等相似，铸体薄片也可得到关于孔隙、矿物的二维结构信息，表征岩石孔隙结构及其配伍关系。与压汞、核磁共振等相比，它具有实验条件简单、对样品规格要求不严、实验周期较短等优点。由于致密岩心孔隙信息的有限性，很难通过铸体薄片的直观鉴定和简单拓扑分析进行孔隙结构的定量描述。本文基于高压压汞和核磁共振实验进行致密岩石的孔隙结构划分，在此基础上应用PSO多阈值分割算法对铸体薄片进行处理得到孔隙-骨架二值图，根据多重分形理论计算孔隙的分形维数和多重分形谱，分析不同孔隙结构的多重分形规律并建立多重分维与核磁、压汞等实验参数的关系，探索基于铸体薄片的致密岩心孔隙结构评价方法。

1 多重分形的基本原理及算法

分形理论已广泛应用于地学研究的各个领域[1-16]，在孔隙结构评价中也起着重要作用，是描述孔隙结构复杂程度的关键技术之一。许多学者已开展了基于核磁共振、毛管压力、铸体薄片、扫描电镜等资料的单重分形维数研究。致密岩石的孔隙分布更加复杂，孔隙结构的局部特性难以通过单一分形维数反映，且往往出现分段特征，影响计算效果。多重分形是在分形理论的基础上发展起来的，可精细刻画研究对象在不同尺度上的分形特征，能反映研究对象在局部区域的变化规律，对致密岩石的孔隙结构表征具有重要意义。

本文应用计盒法简单描述多重分形的基本原理。对具有孔隙-骨架二值特征、像素大小为N×N(N=2m)的图像，若用面积为ε×ε(ε=20，21，…，2m)的正方形去覆盖，共可将样本分成N(ε)个盒子。尺度ε下第i个盒子中孔隙所占像素记为Mi，因此该盒子的概率测度Pi(ε)可表示为[16-25]：

(1)

对具有多重分形特征的岩石孔隙系统，概率测度与尺度ε符合幂指数关系[16-25]：

Pi(ε)∝εai。

(2)

式中：ai称为Lipschitz-Hölder指数或奇异强度，反映第i个盒子中孔隙的分布密度。

根据式(2)可知，不同盒子间可能具有相同的奇异强度，用Na(ε)表示在尺度ε下奇异强度分布在a和a+da间的盒子数，则Na(ε)与ε存在以下关系：

Na(ε)∝ε-f(a)。

(3)

式中：f(a)称为多重分形谱，与奇异强度a有关；a的取值范围可为(-∞,+∞)。

多重分形谱函数f(a)是一个单调函数，在下式成立时其值最大[16-25]：

(4)

式中：q为阶矩或权重因子，其取值范围为(-∞,+∞)。

定义配分函数

(5)

式中：Dq为q阶矩对应的分形维数。

据式(5)可得多重分形维数的计算公式[17-26]

(6)

根据式(3)及式(5)可知，当阶矩q为0时，式(6)可写为：

(7)

当阶矩q为1时，式(6)可写为：

(8)

当阶矩q为2时，式(6)可写为：

(9)

式(7)至式(9)中，D0、D1和D2分别称为容量维、信息维和关联维，是多重分形维数的特殊形式。

同样，可定义质量函数[16-25]

(10)

根据式(6)及式(10)可知，质量函数与多重分形维数的关系可写为[16-25]

τ(q)=(1-q)Dq。

(11)

根据勒让德变换可得奇异强度a(q)、多重分形谱f(a)与质量函数τ(q)的关系

(12)

(13)

还可定义谱宽[16-25]

Δa=amax-amin。

(14)

最常用于表征孔隙结构的是多重分形维数Dq以及多重分形谱f(a)、奇异强度a(q)和谱宽Δa等。一般而言，多重分形维数越大则孔隙结构越复杂，谱宽越大则多重分形特征越明显。

2 致密岩石孔隙结构的多重分形特征

为了定量研究致密岩石的孔隙结构特征，需要对铸体薄片进行处理以得到孔隙-骨架二值图。从铸体薄片中提取孔隙信息的本质是图像分割问题，图像分割算法总体上可分为基于纹理信息分割、基于阈值、基于属性聚类、基于区域分裂和合并等4种基本方法。本文应用文献[28]提出的基于PSO多阈值分割算法从致密岩石铸体薄片中提取出孔隙信息，算法基本原理和流程可见文献[28-30]。

首先根据核磁共振和高压压汞实验将研究区致密岩石按孔隙结构特征分为3类。图1中(a)、(b)、(c)分别是3种孔隙结构完全含水时核磁共振响应、高压压汞毛管压力曲线和基于高压压汞毛管压力的孔喉半径分布图。从A类到C类，岩石物性逐渐变差，核磁共振谱面积逐渐变小，T2向左移动；孔喉半径逐渐由双峰向单峰过渡，孔喉半径逐渐减小。

图2是根据核磁共振和压汞实验分析所得的3类孔隙结构岩石典型的铸体薄片。铸体薄片与核磁共振、高压压汞毛管压力曲线具有较好的对应性，从A类到C类，铸体薄片视域内面孔率越来越小，孔隙连通性越来越差，储集空间类型逐渐由粒内溶孔向晶间孔、 微裂缝过渡。 图3是应用PSO算法进行阈值分割后得到的孔隙-骨架二值图，与图2对比可知，经过阈值分割后蓝色铸体部分被较好地提取出来。对阈值分割后的面孔率与气测法孔隙度进行对比可知，两者的平均绝对误差为0.75%，平均相对误差为6.94%，可见阈值分割法的精度较高。

图4分别为3种孔隙结构岩石的多重分形计算结果(阶矩范围为[-5，5])。图4(a)为多重分形维数D(q)与阶矩q的关系。无论是何种孔隙结构，多重分形维数与阶矩均呈二段式分布，在阶矩较小时D(q)与q成反比且变化剧烈，在阶矩较大时D(q)受q影响较小；从A类到C类，同一阶矩下D(q)呈增大趋势，说明孔隙结构的复杂程度逐渐增大。图4(b)是质量函数τ(q)与阶矩q的关系，整体上τ(q)与q成反比，但τ(q)与孔隙结构的变化关系较为复杂，q较小时τ(q)从A类到C类逐渐增大，q较大时τ(q)从A类到C类逐渐减小。图4(c)是多重分形谱f(a)与奇异强度a(q)的关系，3种孔隙结构均具有极强的多重分形特征(谱宽大于0)，从A类到C类逐渐变大；从A类到C类谱宽、f(a)和a(q)均呈增大的趋势，曲线变化相对变复杂，说明孔隙的分布越来越不均匀。

图2 致密岩石3种孔隙结构的铸体薄片Fig.2 Typical thin sections of three types of tight rocks

图3 基于PSO分割后的孔隙-骨架二值图Fig.3 Pore-matrix binary map from threshold segmentation of thin section (by PSO optimization)

图4 致密岩石3种孔隙结构的多重分形特征Fig.4 Multifractal features of three types of pore structures in tight rock

为定量分析孔隙结构与多重分形参数的关系，针对每块样品进行了4个视域的多重分形研究，并将计算得到的多重分形维数(阶矩范围为[-5，5])取平均值得到岩石整体的多重分形特征。表1是3种孔隙结构的多重分形维数统计结果。从表1可知，多重分形维数从A类到C类均呈增大的趋势且Dmin的变化最明显。常用的分维数如D0、D1、D2也随着孔隙结构的变差而增大，D0在3种分维数中变化最大，D1、D2的变化十分有限，这说明在孔隙结构的单重分形研究中更应注重D0的变化。

表1 致密岩石3种孔隙结构的多重分形维数统计结果Tab.1 Multifractal dimension distributions of three types of pore structures in tight rock

注：表中数据为最小值至最大值，其下的值为这二者的平均值。

选择Dmin和D0作为分形表征参数并研究它们与核磁共振和压汞孔隙结构参数的关系。图5分别为Dmin和D0与中值压力、平均孔喉半径、T2几何平均值之间的关系，式(15)至式(20)分别为Dmin和D0与中值压力、平均孔喉半径、T2几何平均值的拟合公式。分析可知，Dmin和D0与中值压力呈正相关，与平均孔喉半径和T2几何平均值呈负相关，说明多重分形维数在表征孔隙结构方面与压汞和核磁共振具有一致性。从拟合的相关系数可知，Dmin与中值压力、平均孔喉半径和T2几何平均值间的相关性要比D0高。

(15)

(16)

Dmin=0.913 7r-0.139 2R2=0.716，

(17)

D0=0.522 8r-0.204 5R2=0.532；

(18)

(19)

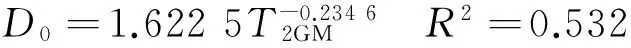
(20)

图5 多重分形维数与微观孔隙结构参数的关系Fig.5 Relationships between multifractal dimension and micro pore structure parameters

3 结 论

(1)多重分形特征能较好地描述致密岩石的孔隙结构特征。不同孔隙结构的岩石具有不同的多重分形特征及多重分形维数。

(2)随着孔隙结构复杂程度的加大及物性的变差，分形维数及谱宽增大；质量函数与阶矩呈典型的二段式分布，阶矩较小时质量函数与孔隙结构复杂程度呈正相关，阶矩较大时质量函数与孔隙结构复杂程度呈负相关。

(3)多重分形维数与孔隙结构复杂程度呈正相关，Dmin的变化最明显；常用的单重分维数中D0与孔隙结构关系最为密切，D1、D2的变化十分有限。

(4)Dmin、D0与中值压力、平均孔喉半径、T2几何平均值呈现较好的相关性，在高压压汞和核磁共振实验数据较少的情况下，可通过铸体薄片的多重分形研究提取多重分形维数进行孔隙结构的定量表征。

[1] KATZ A J,THOMPSON A H.Fractal sandstone pores:implications for conductivity and pore formation[J].Physical Review Letters,1985,54(12):1325-1328.

[2] 贾芬淑，沈平平，李克文.砂岩孔隙结构的分形特征及应用研究[J].断块油气田，1995,2(1)：16-21. JIA Fenshu,SHEN Pingping,LI Kewen.Study on the fractal characteristics of sandstone pore structure and its application[J].Fault-Block Oil and Gas Field,1995,2(1):16-21.

[3] 刘松玉，张继文.土中孔隙分布的分形特征研究[J].东南大学学报，1997,27(3)：129-132. LIU Songyu,ZHANG Jiwen.Fractal approach to measuring soil porosity[J].Journal of Southeast University,1997,27(3):129-132.

[4] 王经洲，郑晓，宛农，等.基于扫描电镜图像分析的菜籽仁饼孔隙结构分形研究[J].农业工程学报，2008,24(3)：16-20. WANG Jingzhou,ZHENG Xiao,WAN Nong,et al.Fractal character of the pore structure of dehulled rapeseed cake based on scanning electron microscopy image analysis[J].Transactions of the Chinese Society of Agricultural Engineering,2008,24(3):16-20.

[5] 孙军昌，周洪涛，郭和坤，等.复杂储层岩石微观非均质性分形几何描述[J].武汉工业学院学报，2009,28(3)：42-46. SUN Junchang,ZHOU Hongtao,GUO Hekun,et al.Characterization of complex rock micro-heterogeneity using fractal geometry[J].Journal of Wuhan Polytechnic University,2009,28(3):42-46.

[6] 彭瑞东，杨彦从，鞠杨，等.基于灰度CT图像的岩石孔隙分形维数计算[J].科学通报，2011,56(26)：2256-2266. PENG Ruidong,YANG Yancong,JU Yang,et al.Computation of fractal dimension of rock pores based on gray CT images[J].Chinese Science Bulletin,2011,56(26):2256-2266.

[7] 葛新民，范宜仁，邓少贵，等.基于分形理论的毛管压力和电阻率指数相关性研究[J].中国石油大学学报(自然科学版)，2012,36(4)：72-76. GE Xinmin,FAN Yiren,DENG Shaogui,et al.Research on correlation between capillary pressure and resistivity index based on fractal theory[J].Journal of China University of Petroleum(Edition of Natural Science),2012,36(4):72-76.

[8] ABDASSAH D,PERMADI P,SUMANTRI Y,et al.Saturation exponents derived from fractal modeling of thin-sections[C].SPE 36978,1996.

[9] 唐红瑛，唐仁骐.砂岩岩心孔隙结构分形特征的探讨[J].中国科学技术大学学报，2004,34(s1)：69-75. TANG Hongying,TANG Renqi.Study on fractal dimensions of sandstone reservoir rock samples pore structure[J].Journal of University of Science and Technology of China,2004,34(s1):69-75.

[10] 唐玮，唐仁骐，白喜俊.分形理论在油层物理学中的应用[J].石油学报，2008,29(1)：93-96. TANG Wei,TANG Renqi,BAI Xijun.Application of fractal dimension theory to reservoir physics[J].Acta Petrolei Sinica,2008,29(1):93-96.

[11] ESSEX,CHRISTOPHER,NERENBERG,et al.Fractal dimension:limit capacity or hausdorff dimension?[J].American Journal of Physics,1990,58(10):986-988.

[12] HARGIS C D,BISSONETTE J A,DAVID J L.The behavior of landscape metrics commonly used in the study of habitat fragmentation[J].Landscape Ecology,1998,13(3):167-186.

[13] HARGROVE W W,HOFFMAN F M,SCHWARTZ P M.A fractal landscape realizer for generating synthetic maps[J].Conservation Ecology,2002,6(1):2.

[14] 孙霞，吴自勤，黄畇.分形原理及其应用[M].合肥：中国科学技术大学出版社，2003.

[15] PATRICIA Tang,NORA Y K Chew,HAK K Chan,et al.Limitation of determination of surface fractal dimension using N2adsorption isotherms and modified Frenkel-Halsey-Hill theory[J].Langmuir,2003,19:2632-2638.

[16] BREWER J,DI Girolamo L.Limitations of fractal dimension estimation algorithms with implications for cloud studies[J].Atmospheric Research,2006,82(1/2):433-454.

[17] 曹汉强，朱光喜，李旭涛，等.多重分形及其在地形特征分析中的应用[J].北京航空航天大学学报，2004,30(12)：1182-1185. CAO Hanqiang,ZHU Guangxi,LI Xutao,et al.Multi-fractal and its application in terrain character analysis[J].Journal of Beijing University of Aeronautics and Astronautics,2004,30(12):1182-1185.

[18] 成秋明.非线性成矿预测理论:多重分形奇异性-广义自相似性-分形谱系模型与方法[J].地球科学:中国地质大学学报，2006,31(3)：337-348. CHENG Qiuming.Singularity-generalized self-similarity-fractal spectrum(3S)models[J].Earth Science:Journal of China University of Geosciences,2006,31(3):337-348.

[19] 王志敬，成秋明.P-A分形模型定量度量糜棱岩变形过程中石英微结构的变化[J].地球科学:中国地质大学学报，2006,31(3)：361-365. WANG Zhijing,CHENG Qiuming.Characterization of micro-texture of quartz myionite deformation process using fractal P-A model[J].Earth Science:Journal of China University of Geosciences,2006,31(3):361-365.

[20] VAZQUEZ E V,FERREIRO J P,MIRANDA J.Multifractal analysis of pore size distributions as affected by simulated rainfall[J].Vadose Zone Journal,2008,7(2):500-511.

[21] PAZ Ferreiro J,VIDAL Vázquez E.Multifractal analysis of Hg pore size distributions in soils with contrasting structural stability[J].Geoderma,2010,160(1):64-73.[22] GARCIA Gutierrez C,SAN Jose F.Multifractal analysis of soil micro and macroporosity using digital images obtained with fluorescent dye[J].Geophysical Research Abstracts,2006,8:11094.

[23] SAN Jose Martinez F,MARTIN M A,CANIEGO F J,et al.Multifractal analysis of discretized X-ray CT images for the characterization of soil macropore structures[J].Geoderma,2010,156(1/2):32-42.

[24] ZHOU H,PERFECT E,LU Y Z,et al.Multifractal analysis of grayscale and binary soil thin section images[J].Fractals-Complex Geometry Patterns and Scaling in Nature and Society,2011,19(3):299-309.

[25] JOUINI M S,VEGA S,MOKHTAR E A.Multiscale characterization of pore spaces using multifractals analysis of scanning electronic microscopy images of carbonates[J].Nonlin Processes Geophys,2011,18:941-953.

[26] KWASNY W,MIKUA J.Fractal and multifractal characteristics of the PVD and CVD coatings deposited onto compound tool ceramics[J].Archives of Materials Science and Engineering,2012,56(1):37-44.

[27] YAO Shanglin,QIN Shenggao,WANG Guohui,et al.Multi-fractal characteristics of the heterogeneous pore distribution of cores[C].International Conference on Computer Distributed Control and Intelligent Enviromental Monitoring,2012:424-427.

[28] GHAMISI P,COUCEIRO M S,BENEDIKTSSON J A,et al.An efficient method for segmentation of images based on fractional calculus and natural selection[J].Expert Systems with Applications,2012,39(16):12407-12417.

[29] SATHYA P D,KAYALVIZHI R.PSO based tsallistresholding selection procedure for image segmentation[J].International Journal of Computer Applications,2010,5(4):39-46.

[30] OMRAN,MAHAMED G H.Particle Swarm Optimization Methods for Pattern Recognition and Image Processing[D].Pretoria :University of Pretoria,2004.

责任编辑：董 瑾

Multifractal Properties of Tight Rock Pore Structure Based on Thin Section

LI Runze1,WANG Changjiang2,LI Wei1,LUAN Dongxiao3,HAN Junzheng4,CUI Haibiao5,LIU Yunze6,LIU Jiaxiong7

(1.The First Natural Gas Production Plant,Qinghai Oilfield Company，Golmud 816000,Qinghai,China; 2.Oil and Gas Evaluation Center,CNPC Logging Co.Ltd.,Xi'an 710077,Shaanxi,China; 3.Research Institute，CNOOC,Beijing 100027，China;4.Geology Institute of The First Oil Production Plant,Huabei Oilfield Company， Renqiu 062552，Hebei，China;5.The Fifth Gas Production Plant,Changqing Oilfield Company，Wushen Banner 017300,Inner Mongnlia，China;6.The First Geological Logging Company,Daqing Drilling Engineering Company,Daqing 163000，Heilongjiang，China;7.Faculty of Earth Science and Technology，China University of Petroleum(East China)，Qingdao 266580，Shandong，China)

The pore structure of tight cores is classified based on mercury injection and NMR core analysis,the cast slices of different pore structure are obtained,and two dimensional pore-matrix graphs of the cast slices are obtained by PSO multi-threshold segmentation algorithm.Multifractal dimension and multifractal spectrum of different types of pore structure are calculated based on the multifractal theory of pore structure,and the relationships between multifractal dimension and median saturation pressure,average pore radius and nuclear magnetic T2geometric mean.The results show that the pore structure characterization method based on multi-fractal has the same effectiveness as mercury injection method and NMR core analysis method.The multi-fractal characteristics of different types of pore structure are different,and the worse the physical properties of cores,the more complex the pore structure,the greater the multifractal dimension.It is also found that the multi-fractal dimension increases with the increase of median saturation pressure,and decreases with the increase of average pore radius and NMR T2geometric mean.Dmin has the strongest correlation with pore structure type and other pore structure characterization parameters,in the absence of mercury penetration and NMR experimental data,the multifractal dimension derived from cast slices can provide a favorable basis for the quantitative characterization of tight rock pore structure.

tight rock;pore structure;multifractal characteristic;cast slice;PSO segmentation

2015-12-05

国家自然科学基金(编号：41404086)；国家重大科学仪器设备开发专项(编号：2013YQ170463)；中国博士后基金(编号：2014M560591)

李润泽(1985-)，男，工程师，硕士，主要从事油气储层地质学及油气藏开发地质研究。E-mail:lrzupc@163.com

DOI:10.3969/j.issn.1673-064X.2016.06.010中图分类号:P631.84文章编号:1673-064X(2016)06-0066-06文献标识码:A