高频波动对多孔弹性介质中稠油黏温参数影响规律研究

蒲春生，徐加祥，刘 玺，郑黎明，刘 静

(1.中国石油大学(华东) 石油工程学院，山东 青岛 266580；2.中国石油大学(华东) 重质油国家重点实验室，山东 青岛 266580；3.延长油田股份有限公司 西区采油厂，陕西 延安 717500)



高频波动对多孔弹性介质中稠油黏温参数影响规律研究

蒲春生1,2，徐加祥1,2，刘 玺3，郑黎明1,2，刘 静1,2

(1.中国石油大学(华东) 石油工程学院，山东 青岛 266580；2.中国石油大学(华东) 重质油国家重点实验室，山东 青岛 266580；3.延长油田股份有限公司 西区采油厂，陕西 延安 717500)

为了定量描述高频波动激励井热力学降黏解堵的机理，基于高频波在多孔弹性介质中能量传播、损耗和转化的动力学特征，建立了高频波动激励下稠油油藏近井带储层中稠油温度及黏度变化的稳态和非稳态耦合动力学模型。该模型由能量衰减和转化方程、非均匀热源圆筒壁导热微分方程和温黏状态方程组成，采用耦合迭代方法进行数值计算，揭示了高频波对多孔弹性介质中稠油温度和黏度影响的主控因素及规律。结果表明：频率为20 kHz的高频波动在r<0.6 m范围内作用效果明显，频率越高作用效果越好，但处理范围越小；与波动频率相比，振幅对其作用效果更显著；波动作用由非稳态向稳态过渡所用时间约400 s。该模型的建立与求解，为稠油油藏近井地带高频波动解堵增产增注技术提供了重要的理论依据。

稠油开采；高频波动；降黏解堵

蒲春生，徐加祥，刘玺，等.高频波动对多孔弹性介质中稠油黏温参数影响规律研究[J].西安石油大学学报(自然科学版)，2016，31(6)：54-59,107.

PU Chunsheng,XU Jiaxiang,LIU Xi,et al.Study on influence of high frequency vibration on viscosity and temperature parameters of heavy oil in porous elastic medium[J].Journal of Xi'an Shiyou University (Natural Science Edition),2016,31(6):54-59,107.

引 言

近几十年来，高频波动采油技术在油田开发过程中取得了比较好的矿场应用效果，成为一种比较典型的物理法提高采收率技术。利用高频波动处理生产井和注水井的近井地带，凭借其力学效应、热学效应和化学效应，可以解除地层堵塞，在油层产生微裂缝，改变流体的物性及流动状态[1]，从而改善近井地带的渗流状况，达到增产增注的目的。

稠油由于其黏度高、凝固点高的特点，矿场普遍采用注热流体加热的方式开发。但是在此过程中，大量高温流体改变了油藏内部孔隙条件，特别是在近井地区引起沥青质沉积，堵塞孔喉，造成注气压力升高[2-3]。高频波动作为一种物理降黏解堵方法，通过波传播过程中能量的衰减及向热能的转化，给稠油加热升温，降低其黏度，达到近井地带降黏解堵的效果。由于饱和流体多孔弹性介质的复杂性，前人的研究普遍局限于室内实验，对其热力学降黏机理大多停留在定性解释的层面[4-7]，对高频波动热力学降黏规律及降黏模型还未形成成熟的理论。

本文从高频波动能量由机械能向热能转化的过程出发，将波动能量衰减和转化方程、非均匀热源圆筒壁导热微分方程和温黏状态方程组合，建立了定量表征高频波参数对多孔弹性介质中稠油黏度和温度影响的耦合动力学模型。采用耦合迭代方法进行数值计算，揭示高频波对多孔弹性介质中稠油温度和黏度影响的主控因素及作用规律。

1 高频波动作用下多孔弹性介质能量衰减与转化动力学模型

在无限大弹性介质中前进的波称为行波，其在传播过程中输送能量和动量，可用波动方程进行描述。假设在无限均匀弹性介质中有一个无限大刚性物体沿法线方向振动，这时所产生的是柱面波动，波动方程为

(1)

式中：ζ为某质点某时刻位移，m；A为某质点最大振幅，m；ω为角频率，rad/s；τ为时间，s；r为质点距振源的距离，m；C0为波动传播速度，m/s。

高频波动在弹性介质中传播时，会带动弹性介质中的质点振动，导致弹性介质中压强出现交替变化。波动场中某一点在某一瞬时所产生的压强p1与没有波场时同一点的静态压强p0之差称为该点的声压[8]，用p表示，即p=p1-p0，

(2)

式中：p为声压，MPa；ρ0为振动质点密度，g/cm3。

设在波动场中取一块足够小的单位体积，在未加载波动前体积为V0，压强为p0，密度为ρ0，在加载波动后，由于波动的扰动使该单位体积得到动能

(3)

式中：V0为体积，cm3；v为质点振动速度，m/s。

同时在该扰动下，该单位体积压强由p0升高到p0+p，于是该单位体积具有的位能

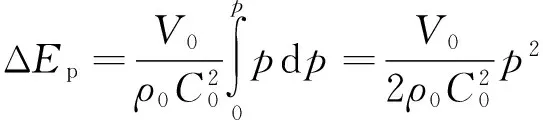
(4)

单位体积内总的高频波动能量为动能和位能之和，即

(5)

式中：ΔE为单位体积机械能，10-3J；ΔEk为单位体积动能，10-3J；ΔEp为单位体积势能，10-3J。

单位体积中高频波动能量称为波动能量密度，表示为

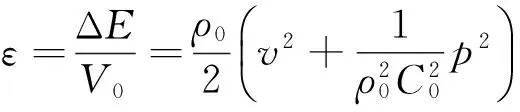
(6)

式中：ε为波动能量密度，10-3J/cm3。

其中振动速度

由式(6)得到高频波动下波动能量密度[9]

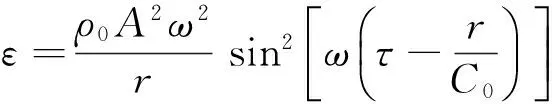
(7)

波的衰减主要表现为其振幅的衰减，衰减形式表现为A=A0e-αr。

其中高频波动与低频相比有较高的衰减系数，其衰减系数[10-11]

exp[-(0.001 622 8.79ρKfμ2)ρKpμ-1]。

(8)

式中：α为衰减系数； K为地层渗透率，μm2； μ为流体黏度，Pa·s； f为振动频率， kHz。

那么，波动能量密度

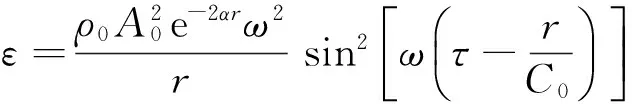
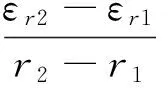
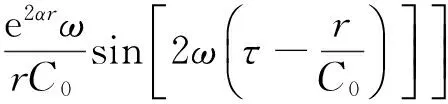
(9)

能量密度在一个周期内的平均值称为平均能量密度，热能的平均能量密度

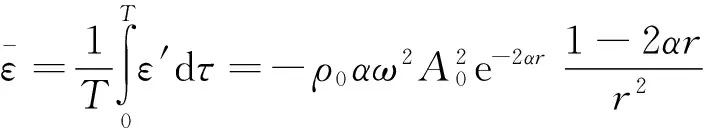
(10)

热能的平均能量密度即为导热微分方程中的内热源，表示为

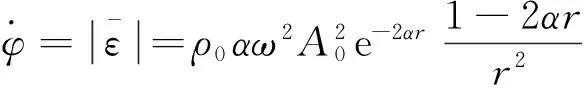
(11)

2 非均匀热源径向导热动力学模型

通过上一节的推导，可以得到高频波动在传播过程中不断衰减，其所具有的机械能向热能转化。为了计算该热能的有效值，推导得到热能的平均能量密度，即单位时间内热能的平均值，也就是导热微分方程的热源项，该热源项中包含了波动的振幅、频率、衰减系数等相关参数。同时高频波动能量在径向上的衰减随振源距离的不同而不同，即导热微分方程中内热源随距离的不同而变化，所以利用稳态非均匀热源的圆筒壁导热微分方程进行推导，并作如下假设：

(1)振动弹性介质是无限大各向同性均匀连续的；

(2)弹性介质的热导率、密度等参数已知；

(3)弹性介质内热源在径向上随振源距离不同而变化，在周向上各点内热源相等，不存在能量传递；

(4)高频波动仅对弹性介质温度和流体黏度有所影响，对其他参数的影响忽略。

采用非均匀热源圆筒壁导热微分方程[12]将热能平均密度作为热源项引入，设定边界条件为无穷远处弹性介质温度不受影响且为原始温度，同时无穷远处导热热能流量为零，即

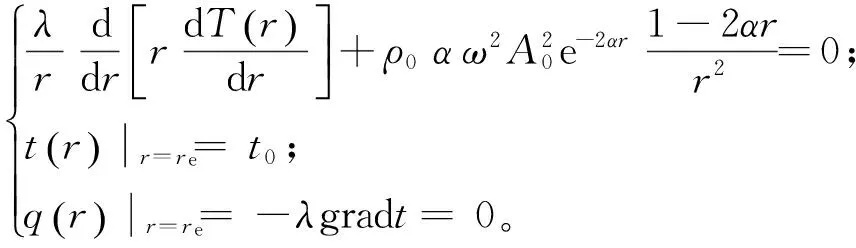
(12)

式中：λ为导热系数，kW/(K·m)；t为波动作用下弹性介质温度，℃；t0为弹性介质初始温度，℃。

上述方程描述了在高频波动作用一段时间后，多孔弹性介质中稠油温度随作用距离变化的稳态方程。现利用非均匀热源圆筒壁非稳态导热微分方程[13-15]结合边界条件和初始条件建立模型(假设条件相同)，描述高频波动作用到达到稳态的过程，即

(13)

式中：τ为振动时间，s。

3 稠油温黏状态方程

上一节中得到了高频波动作用下稠油温度变化的偏微分方程及求解条件，从中可以看出温度是波动衰减系数的函数，而高频波动衰减系数又是黏度的函数，同时黏度对温度比较敏感，因此，需要利用黏度预测模型对温度变化后流体黏度进行预测。油气工业中常用的黏度预测模型有LBC黏度模型、CS黏度模型、LLS黏度模型、PT 黏度模型和PR黏度模型。经过前人的研究发现PR黏度模型在预测黏度时总平均误差最小。本文采用PR模型来预测波动作用下储层稠油黏度的变化，并进行耦合迭代运算。

已被广泛应用的PR模型的形式如下[16-18]：

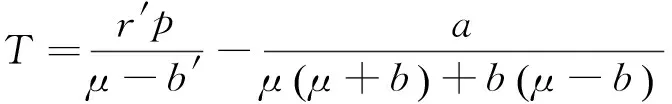
(14)

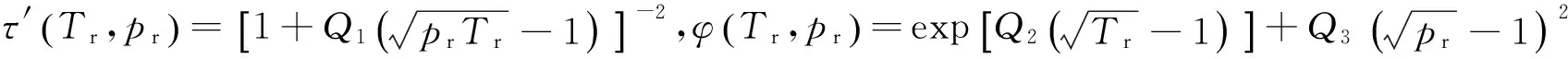
Q1～Q3已经普遍化为偏心因子的关联式。

对于Ec<0.3，有

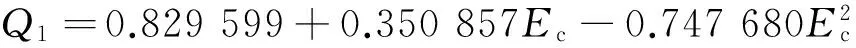
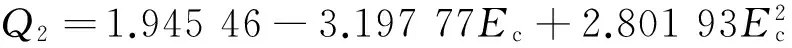
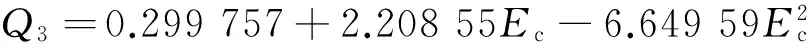
(15)

对于Ec≥0.3，有

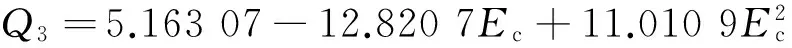
(16)

式中：T为温度，K；Ec为偏心因子；Z为压缩因子；pc为临界压力，MPa；Tc为临界温度，K；pr为对比压力，MPa；Tr为对比温度，K；Mw为分子量，g/mol。

可用解析法求出μ的3个根，在对应温度、压力下，流体黏度取值的判据如下：

(1)在汽、液两相区，饱和汽、液相的黏度分别大于b′的最小实根和最大实根；

(2)在单一液相区和超临界区(T>Tc)，流体黏度取方程的最大实根；

(3)在压力低于流体所处温度下的饱和蒸汽压的气相区时，流体黏度大于b′的最小实根。

应用于混合物的黏度计算时，PR黏度方程可以表示为

(17)

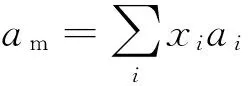
4 稠油黏温耦合模型的求解

基于上述所建模型，采用耦合迭代的方法进行求解，对于距离振源ri处的某点，不同频率和振幅下其黏度和温度变化计算流程如下：

(1)查询并计算模型求解所必须的基础物性参数，如油藏温度、压力，稠油临界温度、压力等；

(2)根据PR黏度预测模型，即式(14)计算未加载波动作用下稠油在油藏条件下的黏度，式(14)中的必要参数在该小节中已列出，同时根据判别条件选取适合的解；

(3)根据衰减系数方程，即式(8)计算该黏度下高频波动的衰减系数；

(4)由所得到的衰减系数以及波动的振幅、频率等参数，利用非均匀热源径向导热动力学方程，即式(12)、式(13)可以分别计算ri处的稠油温度；

(5)利用PR黏度预测模型，即式(14)预测该温度下稠油的黏度；

(6)将步骤(5)中得到的稠油黏度与之前的稠油黏度比较并计算误差，若在误差允许范围内则停止计算，若不满足误差要求则重复步骤(3)—(6)；

(7)由此得到高频波动作用下距离振源ri处稠油黏度及温度的变化，继续向油藏深处推进计算距离振源ri+1处稠油黏度及温度的变化。

5 结果与讨论

基于上述迭代计算流程给出计算所需要的基本数据[19]如表1所示，在基本数据的基础上利用MATLAB编程运算并绘制图形，讨论高频波动在多孔弹性介质中对稠油黏温参数的影响规律。

5.1 波动频率对稠油黏温参数影响规律

不同波动频率(10 kHz、20 kHz、30 kHz)作用下稠油温度及黏度随作用距离的变化见图1，这里保持振幅为1×10-5m。

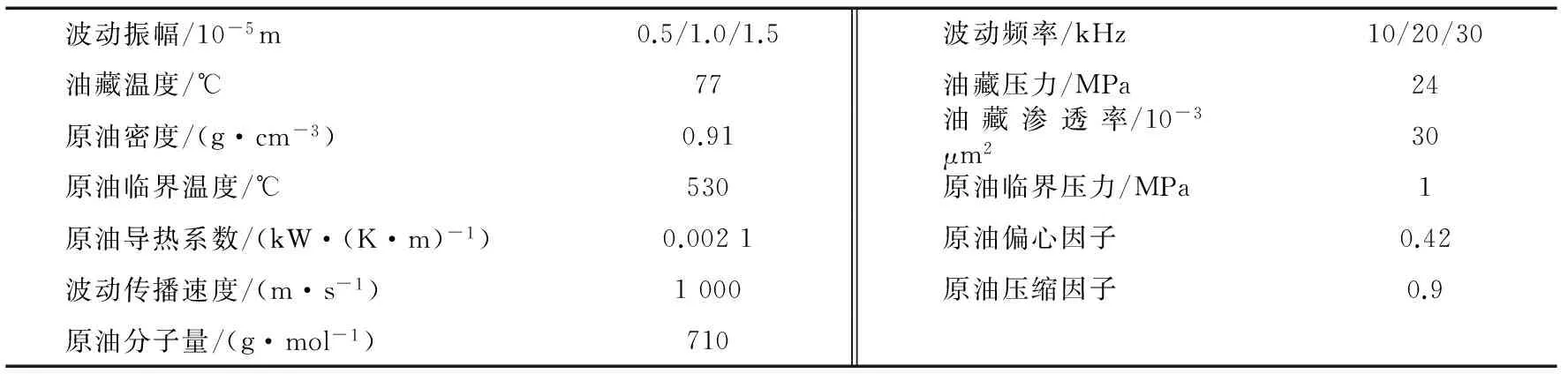
表1 波动作用下稠油黏温模拟基本数据表Tab.1 Basic data for viscosity-temperature simulation of heavy oil under vibration

由图1可以看出，高频波动对稠油温度和黏度的影响近似呈指数变化，距振源由近至远温度呈指数衰减，流体黏度呈指数升高，有效作用范围在0.6 m左右，与实验中超声波处理油层半径范围近似，这是由于波动较高的频率导致其衰减系数较大，波动能量在近井地带就得到较大损耗，无法作用于较远距离的油层。

图1 不同波动频率下稠油温度及黏度随作用距离变化曲线Fig.1 Variation of temperature and viscosity of heavy oil with radial distance under different vibration frequencies

同时由图1可以看出，随着波动频率的提高，近井地带温度升高，流体黏度降低，但是温度的增加量和黏度的减小量在降低。同时随着频率的提高，远井地带在频率较高的波动作用下，油层温度较低，稠油黏度较高。20 kHz曲线与10 kHz曲线的交汇点(即2个频率的等效作用点)在0.18 m左右，30 kHz曲线与20 kHz曲线的交汇点在0.10 m左右，这是由于波动频率越高，衰减系数越大，其能量集中损耗在近井地带，对于远井地带的作用反而不如频率较低的波动，同时也印证了高频波动有较好的近井处理效果，而低频波动有较大处理范围的结论。

5.2 波动振幅对稠油黏温参数影响规律

不同振幅(0.5×10-5m、1×10-5m、1.5×10-5m)的波动作用下稠油温度和黏度随作用距离的变化见图2，这里保持波动频率为20 kHz。

由图2可以看出，不同振幅下，波动对稠油温度及黏度的影响依然表现为指数形式，同时相对于波动频率，振幅对波动作用效果有比较大的影响(在频率和振幅提高幅度相同的条件下比较)，随着振幅的提高，近井地带多孔弹性介质温度加速升高而流体黏度加速降低，这是由于波动的能量与振幅的平方成正比，振幅的改变会导致波动能量的大幅变化。另一个方面，随着振幅的提高，高频波动的处理范围增大，振幅为5 μm时其作用范围约为0.4 m，15 μm时其作用范围约为0.7 m。原因是在衰减因子相同的情况下，振幅提高，波动能量提高，可以传播更远的距离。通过计算可以得到，3种振幅由高到低，平均降黏率分别为31.06%、16.96%、6.46%，平均温度升高率分别为58.45%、29.94%、9.69%。

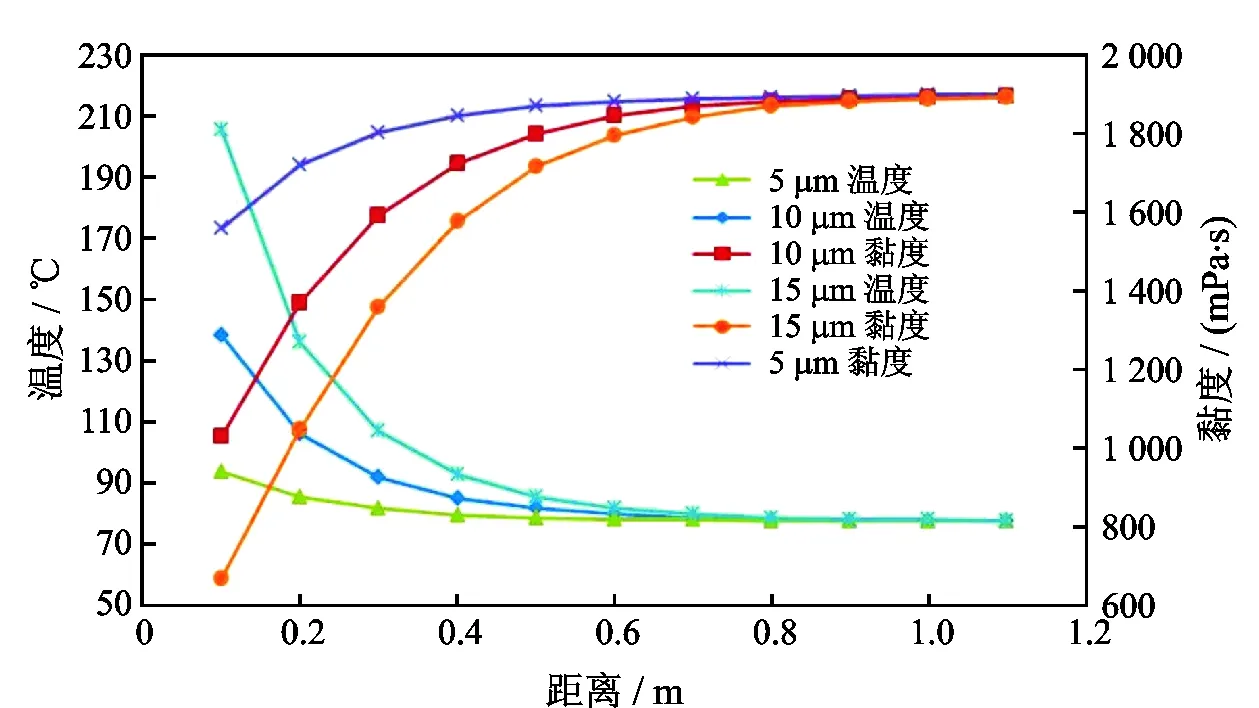
图2 不同振幅下稠油温度及黏度随作用距离变化曲线Fig.2 Variation of temperature and viscosity of heavy oil with radial distance under different vibration amplitudes

5.3 高频波动下稠油温度和黏度随作用时间、作用距离的变化规律

在振幅为10 μm、频率为20 kHz的高频波动作用下，稠油温度和黏度随作用时间和作用距离的变化如图3所示。

由图3可以看出，近井地带随着作用时间的增长，稠油温度不断升高，但是升高的速度逐渐变缓，相对应的，稠油黏度不断降低，但降低的速度逐渐变缓。分析原因是由于随着高频波动的作用，近井地区的温度升高，单位距离的温差增大，导致径向热量传递加快，最终在某一温差下波动提供的热量与径向散失的热量平衡，近井地带稠油的温度和黏度便趋向于平稳。由高频波动开始作用至稠油温度和黏度趋于稳定，所用时间大约是400 s，最终在稳态下稠油温度和黏度变化规律(作用效果、变化趋势、有效作用距离等)与5.1中的计算结果相符。

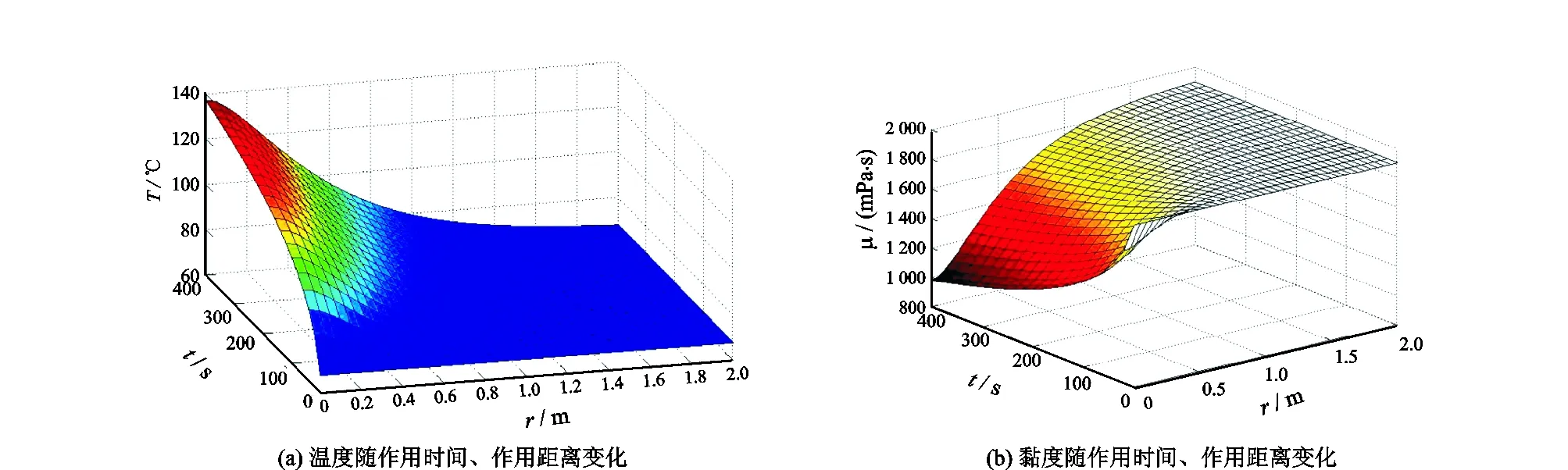
图3 高频波动下稠油温度和黏度随作用时间、作用距离变化关系Fig.3 Variation of temperature and viscosity of heavy oil with time and radial distance under high frequency vibration

6 结 论

(1)高频波在多孔弹性介质中的指数式衰减导致近井地带温度及流体黏度也呈指数形式变化，有效作用距离在0.6 m左右，与以往的实验结果近似。同时30 kHz与20 kHz波动的等效作用距离为0.1 m，而20 kHz与10 kHz为0.18 m，印证了高频波动有较好的近井处理效果，而低频波动有较大的处理范围。

(2)相对于频率，振幅对近井地带温度和黏度的影响更加明显。在波动频率为20 kHz、振幅15 μm下，近井地带平均降黏率为31.06%，平均温度升高率为58.45%。由高频波动开始作用至稠油温度和黏度趋于稳定，所用时间大约是400 s。

(3)根据本文结果，波动近井解堵不宜采用过高的振动频率，否则波场在近井地区衰减过快，无法实现良好的解堵效果。同时提高振动功率也就是振幅可以明显改善作用距离和效果。若要处理油藏内部宜采用作用距离更远的低频振动。

[1] 胡博仲.波场采油[M].北京:石油工业出版社,1996:31-36.

[2] GUO Xiao,DU Zhimin,FU Yu,et al.Effect of formation damage to production performance in heavy oil reservoir via steam-injection after water-flooding[C].SPE 97869,2005.

[3] 张人雄,向阳,李晓梅.超稠油油藏热采过程中沥青质损害室内模拟[J].石油勘探与开发,2001,28(1):85-86. ZHANG Renxiong,XIANG Yang,LI Xiaomei.Asphaltene damage simulation in super heavy oil reservoir during thermal recovery process[J].Petroleum Exploration and Development,2001,28(1):85-86.

[4] 朱静,李传宪,杨飞,等.稠油降黏新技术的研究进展[J].西安石油大学学报(自然科学版),2012,27(1):64-70. ZHU Jing,LI Chuanxian,YANG Fei,et al.Research progress in new viscosity-reducing techniques for heavy oil[J].Journal of Xi’an Shiyou University(Natural Science Edition),2012,27(1):64-70.

[5] 谷潇雨,蒲春生,王蓓,等.超声波解除岩心钻井液堵塞实验研究[J].西安石油大学学报(自然科学版),2014,29(1):76-79. GU Xiaoyu,PU Chunsheng,WANG Bei,et al.Experimental study on removing drilling fluid damage of core by ultrasonic[J].Journal of Xi’an Shiyou University(Natural Science Edition),2014,29(1):76-79.

[6] 蒲春生,石道涵,赵树山,等.大功率超声波近井处理无机垢堵塞技术[J].石油勘探与开发,2011,38(2):243-248. PU Chunsheng,SHI Daohan,ZHAO Shushan,et al.Technology of removing near wellbore inorganic scale damage by high power ultrasonic treatment[J].Petroleum Exploration and Development,2011,38(2):243-248.

[7] 傅俊萍,李录平,刘泽利,等.超声波除垢与强化传热实验研究[J].热能动力工程,2006,21(4):355-357. FU Junping,LI Luping,LIU Zeli,et al.Experimental study on ultrasonic scale removal and heat transfer enhancement[J].Journal of Engineering for Thermal Energy and Power,2006,21(4):355-357.

[8] 王仲茂.振动采油[M].北京:石油工业出版社,2000.

[9] 杜功焕,朱哲民,龚秀芬.声学基础[M].南京：南京大学出版社,2001:190-192.

[10] BIOT M A.Mechanics of deformation and acoustic propagation in porous media[J].Journal of Applied Physics,1962,33(4):1482-1498.

[11] 张全兴.超声波非均匀介质传播衰减特性研究[D].沈阳:沈阳工业大学,2015.

[12] 黄晓齐,龚德鸿,李环.非均匀内热源圆筒壁稳态导热微分方程的热流分流和叠加[J].贵州大学学报(自然科学版),2001,30(3):9-12. HUANG Xiaoqi,GONG Dehong,LI Huan.Heat flow distributing and stacking of non-uniform heat source cylinder steady heat-conduction differential equations[J].Journal of Guizhou University(Natural Science Edition),2001,30(3):9-12.

[13] 戴锅生.传热学[M].2版.北京:高等教育出版社,1999.

[14] 王永岩,秦楠,苏传奇.无限大平板非稳态导热过程的数字特征[J].青岛科技大学学报(自然科学版),2013,34(5):511-515. WANG Yongyan,QIN Nan,SU Chuanqi.Research on numerical characteristics of unsteady heat conduction of an infinite plat[J].Journal of Qingdao University of Science and Technology(Natural Science Edition),2013,34(5):511-515.[15] 顾祥红.无限大平板非稳态导热理论分析[J].沈阳工业大学学报,2009,31(1):112-115. GU Xianghong.Theoretical analysis of unsteady-state thermal conduction of infinite plate[J].Journal of Shenyang University of Technology,2009,31(1):112-115.

[16] 郭绪强,荣淑霞,杨继涛,等.基于PR状态方程的黏度模型[J].石油学报,1999,20(3):56-61. GUO Xuqiang,RONG Shuxia,YANG Jitao,et al.The viscosity model based on PR state equation[J].Acta Petrolei Sinica,1999,20(3):56-61.

[17] 雷宇.稠油黏度预测模型研究[D].成都:西南石油大学,2012.

[18] 冯国强,陈爽,郭绪强,等.油藏流体黏度预测模型的对比分析[J].油气地质与采收率,2007,14(5):80-83. FENG Guoqiang,CHEN Shuang,GUO Xuqiang,et al.Comparative analysis of reservoir fluid viscosity prediction model[J].Petroleum Geology and Recovery Efficiency,2007,14(5):80-83.

[19] 王欣,赵法军,刘江,等.稠油比热容导热系数及黏温物性参数变化研究[J].化工科技,2012,20(3):10-13. WANG Xin,ZHAO Fajun,LIU Jiang,et al.Research on thermal transmissivity heat coefficient and temperature-viscosity parameters changes of heavy oil[J].Science & Technology in Chemical Industry,2012,20(3):10-13.

责任编辑：贺元旦

Study on Influence of High Frequency Vibration on Viscosity and Temperature Parameters of Heavy Oil in Porous Elastic Medium

PU Chunsheng1,2,XU Jiaxiang1,2,LIU Xi3,ZHENG Liming1,2,LIU Jing1,2

(1.Faculty of Petroleum Engineering,China University of Petroleum (East China),Qingdao 266580,Shandong,China;2.State Key Laboratory of Heavy Oil Processing,China University of Petroleum (East China),Qingdao 266580,Shandong,China;3.Western Oil Production Plant,Yanchang Oilfield Company,Yan'an 717500,Shaanxi,China)

In order to quantitatively describe the thermodynamic viscosity-reducing and plug-removing mechanism of high-frequency vibration excitation near wellbore,the steady and unsteady coupling dynamic models of heavy oil temperature and viscosity variation near wellbore of heavy oil reservoir caused by high-frequency vibration excitation are established respectively based on the energy transmission,loss and transformation kinetics of high-frequency vibration wave in poroelastic medium.The models consist of energy attenuation and transformation equation,the differential equation of inhomogeneous heat source conduction in cylindrical wall and the temperature-viscosity equation of heavy oil,and they are solved using coupling iterative method to reveal the main controlling factors and laws of high-frequency vibration influencing the temperature and viscosity variation of heavy oil in poroelastic medium.The results show that the vibration of 20 kHz has a better effect within 0.6m;the higher the frequency of vibration,the better the viscosity-reducing and plug-removing effect of vibration,but the smaller the effect range of vibration;compared with vibration frequency,vibration amplitude has greater effect;it takes about 400 s for the effect of vibration to transit from non-steady state to steady state.

recovery of heavy oil;high-frequency vibration;viscosity-reducing and plug-removing

2016-08-30

国家“863”计划重大专项课题“超大功率超声波油井增油技术及其装置研究”(编号:2007AA06Z227)；山东省自然科学基金“稠油热波耦合辅助层内化学催化裂解降黏技术研究”(编号:ZR2010EM014)；中国石油化工股份有限公司重大科技专项项目“稠油注蒸汽热波耦合催化裂解降黏技术研究”(编号:[2011]075)

蒲春生(1959-)，男，教授、博士生导师，主要从事特种油气藏改造与物理-化学增产增注理论与技术研究。 E-mail:chshpu@163.com

10.3969/j.issn.1673-064X.2016.06.008

TE345

1673-064X(2016)06-0054-06

A