连续波泥浆脉冲器控制策略研究
闫宏亮,石文龙,2,张奇志
(1.西安石油大学 陕西省油气井测控技术重点实验室,陕西 西安 710065;2.新天科技股份有限公司 研发中心,河南 郑州 450001)
连续波泥浆脉冲器控制策略研究
闫宏亮1,石文龙1,2,张奇志1
(1.西安石油大学 陕西省油气井测控技术重点实验室,陕西 西安 710065;2.新天科技股份有限公司 研发中心,河南 郑州 450001)
首先对转阀和驱动电机控制系统进行建模仿真,然后采用频移键控和相干解调方式仿真研究了连续波脉冲器的数据传输过程。通过仿真发现,当考虑通道噪声时,由于滤波环节性能已很难再改善,采用PI控制策略无法正确解调,故采用滑模控制改善电机动态性能,从而实现了正确解调。说明研究控制策略提高驱动电机动态性能有利于提高信号传输质量。这对于连续波脉冲器的实物制作具有重要的参考价值。但是并未考虑传输过程中出现的信号衰减和延迟等情况,仿真中仅用高斯噪声模拟了信道中的噪声,这些问题有待进一步地研究解决。
连续波泥浆脉冲器;永磁同步电机;MATLAB;FSK;仿真
闫宏亮,石文龙,张奇志.连续波泥浆脉冲器控制策略研究[J].西安石油大学学报(自然科学版),2016,31(6):97-103.
YAN Hongliang,SHI Wenlong,ZHANG Qizhi.Research on control strategy of continuous wave mud pulser[J].Journal of Xi'an Shiyou University (Natural Science Edition),2016,31(6):97-103.
引 言
随钻测量是指在钻井过程中对诸如井斜角、方位角和工具面角等井下参数进行实时测量,再将测量信息及时上传至地面,然后加以分析处理的过程。通过对井下测量信息的分析,可及时有效地进行综合地层评价,对钻井轨迹及时纠偏,完善钻进过程[1]。
连续波泥浆脉冲器是无线随钻测量的一种,其成本适中,性能可靠,制造工艺较为简单,相比于传统的正脉冲器,传输速率有很大提升,应用前景可观。但目前该技术仅被国外少数公司垄断,所以研究其数据传输过程,对于制造我国自主知识产权产品,满足我国日益增长的钻井作业需求,提高随钻测量的技术水平具有重要意义。
1 转阀数学建模与仿真
连续波脉冲器的节流阀由具有相同叶片数的定子和转子组成。在电机驱动下,转子对应定子的位置不断发生改变,使泥浆流通面积发生变化,由此引起节流效应从而形成钻井液连续压力脉冲;然后将井下测量信息调制在钻井液脉冲信号上,沿钻柱方向上传,由地面设备检测脉冲信号,通过解码得到井下参数实时信息[2-3]。现在对其重要部件转阀进行建模。
连续波泥浆脉冲发生器中的转阀压力脉冲的方程为[4]

(1)
式中:Q为流过泥浆脉冲器的泥浆流量,m3/s;Cd为泥浆脉冲器的流量系数;ρ为泥浆的密度,kg/m3;Δp为转阀两侧的压差,MPa;A为转阀的流通面积,m2。
由式(1)可知,在Q、ρ、Cd一定的情况下,转阀的两侧压差的变化只和转阀的流通面积有关。故而求出转阀的流通面积,就可以得出转阀的压差变化。转阀的压力脉冲最大幅值设计为3.6 MPa,最小幅值为0.09 MPa。据此设计的转阀定子如图1所示,定子孔角:α1=42°,定子叶片角度:π/2-α1=48°,定子半径R1=43 mm;转子如图2所示,转子孔角:α2=40°,转子叶片角度:π/2-α2=50°,转子半径R2=40.1 mm,d=15.5 mm,Q=0.02 m3/s,ρ=1.1×103kg/m3,Cd=0.7。下面对转阀一个周期的面积变化进行建模。

图1 脉冲器定子图Fig.1 Stator of pulser

图2 脉冲器转子图Fig.2 Rotor of pulser
(a)转阀流通面积上升阶段
转子叶片刚好全部堵在定子孔口,未被堵住的部分形成最小流通通道。整个持续时间转过的角度为π/2-α1-α2=8°。最小流通面积即为图3中斜线部分的面积

(2)
以转子转过的角度β进行分段,取转阀最小流通面积时刻作为起始位置(如图3所示):0<β<40°是流通面积的上升阶段。流通面积为
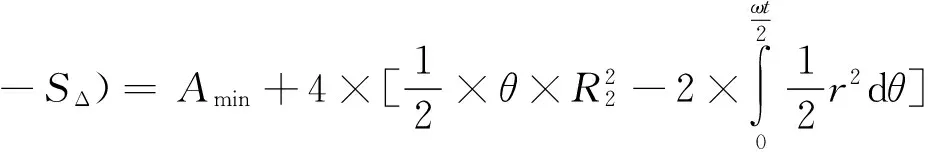
(3)

40°<β<42°是转阀流通面积保持最大的阶段,最大面积即为图4中斜线部分的面积

(4)

图3 转阀最小流通面积图Fig.3 Minimum flow area of rotary valve

图4 转阀最大流通面积图Fig.4 Maximum flow area of rotary valve
(b)转阀流通面积下降阶段
以转子转过的角度进行分段:42°<β<82°是转阀流通面积的下降阶段。流通面积为


(5)

82°<β<90°是转阀流通面积保持最小的阶段。
2 转阀驱动电机控制系统的建模
连续波脉冲器转阀控制电机需要安装在钻铤内,所以要求体积小、惯性小、转矩大、维护工作量小。而永磁同步电机具有结构简单、体积小、功率密度大、效率高等特点,适合用作转阀控制电机。电机参数如下:额定电压48 V,额定转速8 410 r/min,极对数1,转动惯量7.63 g·cm2,R=1.79 Ω,L=0.313 mH。
控制系统采用矢量控制的方法[5-7],使定子电流励磁分量id=0。永磁同步电机定子由三相SVPWM逆变器供电,转子位置传感器检测转子转速n和转角θ。由转速外环和电流内环调节并经过反PARK变化得到SVPWM调制器的电压调制信号。检测到的定子电流经CLARKE变换和PARK变换,得到定子电流id和iq作为电流的反馈信号。
文献[8]中介绍了泥浆脉冲器的转子水力转矩,通过三维流场仿真分析软件CFD对影响水力转矩的几个因素进行了分析。主要影响因素有定转子间隙、转子的转速、泥浆的流量和转阀开度。采用类似的分析处理方法,针对本文所设计的转阀,通过CFD软件分析得到转阀的原始数据。设定转子间隙为6 mm,流量为0.03 m3/s,那么在定转子间隙、流量一定的条件下,水力转矩仅与转阀开度有关,两者近似形成一个曲线关系。因为CFD软件分析处理得到数据所需要的时间太久,这样不利于进行MATLAB仿真。所以考虑在MATLAB中进行曲线拟合,得到水力转矩的近似表达式,以函数的方式作用在永磁同步电机上,以考虑其对电机调速的影响。转阀驱动电机控制系统总体仿真图见图5。

图5 转阀驱动电机控制系统仿真图Fig.5 Simulation of rotary valve control system driven using motor
3 连续波泥浆脉冲器的FSK信息调制与解调仿真
连续波泥浆脉冲器的信息传输采用2FSK调制[9-10],将井下信息的数字信号调制在2个不同频率的载波信号上,采用相干解调方法进行解调。设低频载波信号的频率为f2,高频载波信号的频率为f1,基带信号的频率为f0。则低频信号对应的带通滤波器的带宽为(f2-f0)~(f2+f0),高频信号对应的带通滤波器的带宽为(f1-f0)~(f1+f0)。为了能够正确解调,要求2个带通滤波器的频带不能重叠,所以有f1-f0≥f2+f0,也即是要求f1-f2≥2f0。
设f0=10 Hz,低频载波在一个调制周期中有4个载波周期,故设f2=40 Hz,由以上分析可设载波信号f1=100 Hz,以f1载波信号传输信息1,f2载波信号传输信息0,使用高斯噪声模拟传输信道中的噪声,忽略传输过程中的信号衰减和延迟。使用Pulse Generator仿真模块产生的脉冲信号模拟井下采集得到的信号,经过2FSK信号调制和永磁同步电机调速,通过转阀产生压力信号,再通过带通滤波器和低通滤波器进行滤波解调,最终得到井下传输的信息。本研究选择低通加高通滤波器来形成带通滤波效果,这样可使带通滤波器上、下截止频率处的幅频特性曲线都比较陡,从而提升滤波性能。系统的总体的MATLAB/SIMULINK仿真图如图6所示,解调结果对比如图7所示。

图6 连续波泥浆脉冲器2FSK信号调制与解调仿真图Fig.6 Simulation of 2FSK signal modulation and demodulation of continuous wave mud pulser

图7 PI控制时的2FSK的数据信息解调结果对比图Fig.7 Comparison of demodulation results of 2FSK data information using PI control
图7(a)是仿真产生的脉冲数字信号的波形图,由图知要传输的信息为10101010;从图7(b)可以看出加入高斯白噪声后,2FSK的信号调制产生的压力脉冲已经被噪声淹没,看不到转阀产生的有用压力脉冲;图7(c)是解调后的波形图,由图易知解调结果错误。此时,通过对滤波器性能的提升已经很难获得正确解调。
对连续波泥浆脉冲器的工作过程进行梳理,比如载波f2=40 Hz的带通滤波器进行滤波时需要30~50 Hz的波通过,而白噪声中有一些该波段的噪声,另外,转阀驱动电机的转速在切换时会产生些许震荡,这也会产生该波段的噪声。那么,可以考虑改进转阀驱动电机的控制策略,以提高电机的调速性能,从而减少由此产生的噪声,进而查看是否可以获得正确解调。
4连续波泥浆脉冲器的控制策略研究
由于2FSK对电机的调速性能要求比较高,如果电机的转速能够在不同的转速之间迅速切换,并且能够快速趋于稳定,那么就能够获得较好的2FSK调制信号。因此,在对PMSM控制策略的改进中,外环速度环的控制器采用滑模控制。
将PMSM的电压方程和磁链方程代入转矩方程中,且Ld=Lq,得
Te=1.5np(ψdiq-ψqid)=1.5npψfiq。
(6)

(7)


(8)
不妨做如下定义,设速度误差为
e=ω*-ω。
(9)
其中,ω*为速度的给定。那么对式(9)求导,可以得到
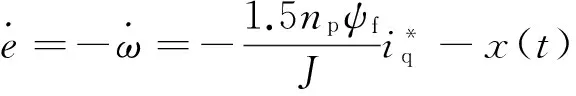
(10)
在以上分析的基础上,对滑模控制中的滑模面进行设计。


(11)
其中,系数c是一个正的常数,选取不同的c值,控制系统就可以获得不同的动态性能。
要求速度的误差能够在有限的时间内到达并维持在滑模面上。故采用等效滑模控制,输出为
u=ueq+usw。
(12)
其中,ueq是滑模的等效控制部分,为的是保证系统的状态在滑模面上。令

(13)
解得

(14)

usw是滑模的切换控制部分,为的是保证系统的状态能够维持在滑模面上,可以做如下定义
usw=ksgn(s)。
(15)
其中,k是一个正常数,sgn(s)是符号函数。
所以,滑模控制律可以设计如下:
u=ueq+usw=Ce+ksgn(s)。
(16)
下面对速度环的滑模控制器进行MATLAB/ SIMULINK建模仿真。速度环的滑模控制器仿真图如图8。其中,K1=6,K2=8,K3=0.8。电流环的PI参数为:KP=15,KI=2。
设电机在0~0.3 s时的转速为1 500 r/min,0.3~0.6 s时的转速为600 r/min。PMSM的转速响应仿真波形图如图9。
相比PI控制时的转速波动率1.6%,由图9可以看出,滑模控制时的转速波动率为0.12%,转速波动已经非常小,调速性能有了很明显的提升。下面按照图6所示的2FSK数据信息的调制解调仿真图进行建模仿真,其中的电机的速度环模块由图8所示的仿真图进行替换。2FSK的数据信息解调结果对比如图10所示。
图10(a)是仿真产生的脉冲数字信号的波形图,由图知要传输的信息为10101010;从图10(b)可以看出加入高斯白噪声后,2FSK的信号调制产生的压力脉冲已经被噪声淹没,看不到转阀产生的有用压力脉冲;图10(c)是通过相干解调法解调后的波形图,由图知解调后的数字信号为10101010。解调结果正确, 只是因滤波而有些许的延迟。 而图8的解调结果出现了较大的问题,无法正确解调。由此可见,对转速环使用滑模控制器进行改进,确实可以使电机获得较好的动态性能,进而实现正确解调。因此,相比于传统的PI调节,对电机的转速环采用滑模控制策略进行改进是有效的。

图8 速度环的滑模控制器仿真图Fig.8 Simulation of sliding mode controller for speed loop

图9 PMSM的转速响应仿真波形图Fig.9 Speed response simulation waveform of PMSM

图10 滑模控制时的2FSK的数据信息解调结果对比图Fig.10 Comparison of demodulation results of 2FSK data information using sliding mode control
5 结 论
(1)首先对转阀和驱动电机控制系统进行建模仿真,然后采用频移键控和相干解调方式仿真研究了连续波脉冲器的数据传输过程。通过仿真发现,当考虑水力转矩的影响时,只有使带通滤波器性能极端优良才可正确解调,而进一步考虑通道噪声时,由于滤波环节性能已很难再改善,采用PI控制策略无法正确解调。
(2)采用滑模控制改善电机动态性能,实现了正确解调。说明研究控制策略提高驱动电机动态性能以及提高信号接收时的去噪性能均利于提高信号传输质量。这对于连续波脉冲器的实物制作具有重要的参考价值。
(3)本文没有考虑传输过程中出现的信号衰减和延迟等情况,仿真中仅用高斯噪声模拟了信道中的噪声,这些问题有待进一步地研究解决。
[1] 闫宏亮,石文龙,李琳.随钻测量信息传输方式的发展现状综述研究[J].重庆科技学院学报(自然科学版),2015,17(6):69-72,83. YAN Hongliang,SHI Wenlong,LI Lin.Research on the status and future of the MWD data transmission[J].Journal of Chongqing University of Science and Technology(Natural Sciences Edition),2015,17(6):69-72,83.
[2] 刘新平,房军,金有海.随钻测井数据传输技术应用现状及展望[J].测井技术,2008,32(3):249-253. LIU Xinping,FANG Jun,JIN Youhai.Application status and prospect of LWD data transmission technology[J].Well Logging Technology,2008,32(3):249-253.
[3] 房军,苏义脑.液压信号发生器基本类型与信号产生的原理[J].石油钻探技术,2004,32(2):39-41. FANG Jun,SU Yinao.The basic types and it's mechanism of the hydraulic signal producer[J].Petroleum Drilling Techniques,2004,32(2):39-41.
[4] 李荣喜,房军.井下旋转压力信号发生器的仿真[J].石油矿场机械,2007,36(2):45-47. LI Rongxi,FANG Jun.The simulation of downhole rotary pressure signal generator[J].Oil Field Equipment,2007,36(2):45-47.
[5] 文家燕,高远,刘传国,等.永磁同步电动机的双闭环分数阶控制研究[J].微特电机,2016,44(1):34-38. WEN Jiayan,GAO Yuan,LIU Chuanguo,et al.Control of PMSM via a double closed-loop fractional-order control strategy[J].Small & Special Electrical Machines,2016,44(1):34-38.
[6] 陈俊硕,刘景林,张颖.永磁同步电机新型矢量控制[J].西安电子科技大学学报(自然科学版),2014,41(4):179-185. CHEN Junshuo,LIU Jinglin,ZHANG Ying.New vector control of the permanent magnet synchronous motor[J].Journal of Xidian University(Natural Science),2014,41(4):179-185.
[7] HAN Yoon Seok,CHOI Jung Soo,KIM Young Seok.Sensorless PMSM drive with a sliding mode control based adaptive speed and stator resistance estimator[J].IEEE Transactions on Magnetics,2000,36(5):3588-3591.
[8] 王智明,肖俊远,菅志军.旋转阀泥浆脉冲器转子水力特性研究[J].石油矿场机械,2012,41(3):1-3. WANG Zhiming,XIAO Junyuan,JIAN Zhijun.Waterpower specialty study of the rotor on rotary valve mud pulser[J].Oil Field Equipment,2012,41(3):1-3.
[9] 孙志雄,谢海霞.基于FPGA的FSK调制解调器设计[J].现代电子技术,2014,37(9):80-82. SUN Zhixiong,XIE Haixia.Design of FSK modulator-demodulator based on FPGA[J].Modern Electronics Technique,2014,37(9):80-82.
[10] 樊昌信,张甫栩,徐炳祥,等.通信原理[M].北京:国防工业出版社,1988:129-155.
责任编辑:董 瑾
Research on Control Strategy of Continuous Wave Mud Pulser
YAN Hongliang1,SHI Wenlong1,2,ZHANG Qizhi1
(1.Shaanxi Key Laboratory of Measurement and Control Technology for Oil and Gas Wells,Xi'an Shiyou University,Xi'an 710065,Shaanxi,China;2.Research and Development Center,Suntront Technology Co.Ltd.,Zhengzhou 450001,Henan,China)
Firstly,the modeling and simulation of rotary valve and motor control system are carried out,and then the data transmission process of continuous wave pulser is simulated by frequency shift keying and coherent demodulation.The simulation results show that,when considering the channel noise,the filter performance is hardly improved,correct demodulation can not be obtained using the PI control strategy.Therefore,the sliding mode control is adopted to improve the dynamic performance of the motor and to achieve correct demodulation.It is showed that the control strategy can improve the dynamic performance of the driving motor and the quality of signal transmission.This has an important reference value for the production of continuous wave pulse generator.But the signal attenuation and delay in the transmission process is not considered,and the noise in the channel is simulated by Gauss noise,which needs to be further studied and solved.
continuous wave mud pulser;PMSM;MATLAB;FSK;simulation
2016-03-15
陕西省教育厅重点实验室科研计划项目(编号:15JS084)
闫宏亮(1975-),男,博士研究生,副教授,主要从事电机控制和电动钻机电气控制系统研究。 E-mail:hlyan@xsyu.edu.cn
10.3969/j.issn.1673-064X.2016.06.015
TE927
1673-064X(2016)06-0097-07
A

