基于有向加权复杂网络的供应链修复机制研究

贺鹤鸣，成耀荣

(中南大学 交通运输工程学院，湖南 长沙 410075)



基于有向加权复杂网络的供应链修复机制研究

贺鹤鸣，成耀荣

(中南大学 交通运输工程学院，湖南 长沙 410075)

为从整体效率出发确定供应链受损后的修复方案，通过调节供应链网络的连边权重来模拟其受损状况，对有限修复资源进行分配，以供应链网络效率为指标寻找最优方案。以BBV(Barrat-Barthelemy-Vespignani)模型为基础，结合企业之间的当量物流量和空间距离计算连边权重，从有向加权复杂网络的角度建立供应链网络模型。结合连接阻力对最短路径公式进行改进，设计出基于节点间平均最小合作阻力的供应链网络效率指标。分别从全局受损和某节点受损进行供应链的修复研究，并且找到效率最优方案。研究结果表明：由于供应链网络的节点、连边之间相互影响，不同的节点、连边组合会产生不同的效果，从供应链网络效率角度考虑修复方案更具全局意义。

供应链；网络效率；复杂网络；BBV；修复机制

供应链是一个动态复杂的系统，由于处于开放的环境中，在运作的过程中会不可避免的受到各种风险[1-2]的影响，如果处理失当，可能会给整个供应链带来重创，例如：1999发生的台湾9.21地震，导致包括戴尔公司和苹果公司在内的整个电脑芯片界一度陷入瘫痪[3]；Ericsso的芯片供应商由于失火无法供货，直接影响到后来Ericsson公司退出手机生产行业[4]。由于危害较大，供应链中断的管理受到越来越多的关注，胡梦飞[5]从风险发生前和风险发生后两个角度对供应不确定情况下的供应链中断风险进行了研究，并且设计了弹性供应链，提出在供应不确定情况提升供应链弹性的措施；刘纯霞等[6]验证了供应链中断风险传导路径的小世界特性，发现核心节点企业的稳定性对供应链中断风险传导过程中供应链网络整体的稳定性起到至关重要的作用；杨小雨[7]引入中断度来描述供应链中断状态，总结中断修复的可用措施并建立了修复措施库，基于马尔可夫决策过程建立了供应链中断修复的动态优化模型。由于供应链本身就是一个复杂的网络系统[8]，相关学者开始运用复杂网络理论[9]对供应链进行研究。Thadakamalla等[10]首先提出了供应链的结构模型，针对军事供应链的特点将网络中的节点进行了分类；杨光华等[11]运用复杂网络理论，提出了以程度中心性、中介中心性、凝聚性、核心-边缘结构性等结构关系指标，构建了区域物流网络结构关系分析的定量化方法；李刚[12]建立了典型的五级供应链网络模型，并且分析了其静态鲁棒性和动态鲁棒性；孟繁华[13]在局域世界演化模型的基础上构建了供应链模型，以传统的最短路径公式为基础考察供应链效率。

相关成果为供应链的修复研究打下了很好的基础，但是从网络角度考虑如何修复供应链的研究非常有限，本文以BBV模型[14]为基础，从有向加权复杂网络的角度建立供应链模型，以节点间连接权重为度量进行修复资源的分配，寻找最优的供应链修复方案。

1 供应链网络演化机制及效率指标设计

1.1 基于BBV的供应链网络演化机制

主要从5个层级考虑供应链的结构：供应商(C1)、生产商(C2)、分销商(C3)、销售商(C4)、消费者(C5)，即：

SC={C1,C2,C3,C4,C5}

其中，每个层级都可以看成是相关实体的集合：

本文考虑的是有向加权网络，设定连边方向与物流方向一致，连边权重大小基于当量物流量[15]q'和空间距离l进行计算，定义邻接矩阵为Aij，邻接矩阵中的元素aij表示节点i和节点j的连接权重，aij=wij。

(1)

式中：wij表示由节点i指向j的边的权值；α表示物资的当量物流量系数；qij为从节点i流向j的实际物流量；sij表示节点i和j之间的空间距离。

基于BBV模型的网络演化机制如下：

1)增长机制：在初始供应链的基础上，每个时间步长，各层级按照一定的数量比例向网络中引入若干节点，Ci层级中每个节点带来Ci-in条入边，Ci-out条出边。供应链中实体间的联系一般只发生在相邻的上下游企业间，局域世界设置为：Local(C1)={C2}；Local(C2)={C1,C3}；Local(C3)={C2,C4}；Local(C4)={C3,C5}；Local(C5)={C4}，其中Local(Ci)为Ci层级节点的局域世界。

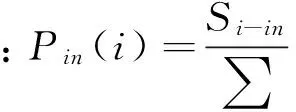
3)权值动态演化：每次新加入的节点n会导致其邻居节点的出入强度发生变化，若新加入的边为入边，即，Si-in=Si-in+wni+δi，wji=wji+Δwji；其中，Δwji=δiwji/Si-in；若新加入的边为出边，即，Si-out=Si-out+win+δi，wij=wij+Δwij；其中，Δwij=δiwij/Si-out。

1.2 供应链网络效率指标设计

对于复杂网络来说，平均路径长度表示产品在经历一系列流程后的平均交付时间，它反映了节点间沟通的便捷程度。网络效率被认定为网络中所有节点对最短路径的倒数的平均数：

(2)

式中：E(G)表示网络的效率；N为节点数量；dij表示节点i和节点j之间的最短路径的长度。

本文的连边权重能够反映节点之间的联系紧密程度。因为企业联系越紧密，合作阻力就越小；联系越松散，合作阻力自然就相对更大，所以将节点间的连接阻力设定为连边权重的倒数，阻力综合考虑了企业间的当量物流量和空间距离，更具合理性，

(3)

式中：ξij表示节点i与节点j之间的连接阻力；wij表示节点i与节点j之间的连边权重。

根据传统的节点间最短路径概念，定义任意两点间的阻力最小路径，利用Floyd算法计算阻力最小路径的长度：

(4)

式中：lij表示节点i与节点j之间的所有路径的阻力大小；zij表示节点i与节点j之间阻力最小路径的长度。

企业之间的连接阻力越小，沟通越顺畅，供应链的效率就越高，传统网络效率的计算方法只考率了节点之间的距离，本文从当量物流量和空间距离考虑节点之间的连接阻力，对其进行改进，将供应链网络效率定义为供应链中所有节点对之间阻力最小路径倒数的平均数：

(5)

从删除节点对网络效率影响大小的角度考察供应链节点的重要性，假设E0为网络的初始效率，Ek为删除某节点k后的网络效率。节点k重要性Ik计算公式为：

Ik=1-Ek/E0

(6)

2 供应链修复机制研究

从全局受损和某节点受损考虑供应链修复机制，研究背景如下：

1)连边权重是衡量节点间联系紧密程度的指标，权值变小，说明节点之间的联系受到破坏，所以通过调节连边权重的大小来模拟供应链的受损状态。如果节点i的效率下降了50%，将i与其邻居节点之间连边的权重降为之前的50%来模拟这种状态。

2)以连接权重为资源的度量，用于修复供应链的资源是有限的，取部分重要性高的受损节点或连边作为候选修复对象，然后在其中进行选择并修复，根据它们的初始强度和权重大小进行资源分配。

2.1 全局受损供应链的修复机制建模

供应链的某处或者某个层级受到不确定性的影响后效率下降，由于节点之间的相互作用，影响逐渐 “传染”到供应链的其它节点，最终可能会造成全局效率下降。例如，发生在2005的“苏丹红”事件，不仅给以“苏丹红”为添加剂的食品生产商造成惨重损失，而且给以“苏丹红”为纽带的原料供应商、分销商、零售商造成了不同程度的损失[16]。对全局受损供应链的修复机制建模如下：

(7)

2)按照节点的强度大小进行资源分配，节点i的分配量p(i)为：

(8)

式中：r为资源总量为；Si为节点i的强度；Ω为进行修复的节点集合。

3)以重要性最高的m0个节点为候选修复对象，从中选取节点进行能力恢复，考虑不同节点个数下的所有组合情况，方案总数为：

(9)

按不同方案进行资源分配后计算供应链网络的效率，找到最优方案。

2.2 节点受损供应链的修复机制建模

在供应链网络的运行过程中，不确定因素很可能导致某个节点受损，邵鲁生等[17]针对某供应节点失效的问题，提出了启用备选供应商、修复失效供应商和重新优化供应计划的综合应急策略；闫妍等[18]研究了供应链某节点失效时供应链弹性应急调度问题，以成本最小为目标函数建立了数学模型。本文从网络的角度出发，考虑在资源有限时如何选择性的修复受损节点与其他节点之间的业务，节点受损供应链的修复机制建模如下：

(10)

其中，τ(i)为与i相连的节点集合。

2)按照连边的权重大小进行资源分配，连边的分配量p(i,j)为：

(11)

式中：资源总量为r；i与Ω中所有节点的连边为修复对象。

3)在以节点i为端点的连边中选择n条作为候选修复对象，从中选取并进行能力恢复，最少修复边数为m，考虑不同连边数量下的所有组合情况，方案总数为：

(12)

按不同方案进行资源分配后计算供应链网络的效率，找到最优方案。

3 算例

3.1 供应链网络的生成

1)初始供应链结构及其连边的权重见图1。参考美国UltraLog计划所用的军事物流网络方面的研究成果[10]，每个步长加入44个节点，各层级节点的数量比例为C1∶C2∶C3∶C4∶C5=2∶1∶4∶12∶25，进行十个步长的演化，网络最终包含461个节点。

2)假定新节点引入的出边和入边数量为：C1-out=1；Ci-in=1,Ci-out=1,(2≤i≤4)；C5-in=1。

3)假设新加入边的权重w服从[wmin,wmax]上的均匀分布，其中wmin表示与该边连接关系相同的边的最小权值，wmax表示与该边连接关系相同的边的最大权值。新引入的边(n,i)给i带来的额外的流量负担δi与新边的权重成正比，将其设定为新边权重的0.1倍。

利用Matlab编程仿真，计算各个节点的强度并按由大到小的顺序进行排列，强度的分布均呈现出较明显的幂律特性，节点强度统计及其概率分布见图2。

图1 初始供应链网络图Fig.1 Network diagram of initial supply chain

图2 网络的节点强度统计及其概率分布Fig.2 Network node intensity statistics and probability distribution

3.2 全局受损供应链修复机制研究

取α=4，r=1 000，m0=10。首先，从方案所含节点个数的角度进行考虑，分别计算不同节点数下所有方案的效率平均值，结果见表1。随着方案包含节点数的增加，平均效率呈逐渐增大的趋势。总体上，将资源分散到更多的节点、修复更多的受损企业，能够取得更高的供应链网络效率。

表1 不同节点数下方案的平均效率

Table 1 Average efficiency of the scheme under different node number

方案所包含节点数供应链网络平均效率/%127.03227.99328.80429.44530.07630.65731.14831.57931.961032.32

对确定节点数下的各个方案进行具体分析，部分结果如图3。

图3 节点数为4、6时各方案的效率Fig.3 Efficiency of each scheme when the number of nodes is 4 and 6

随着方案序号的增大，供应链效率值在波动中整体缓慢下降，中间偶尔出现较大波动。候选节点是按重要性的降序进行排列的，重要的节点相对集中在序号值较小的方案中，优先恢复它们的能力可以得到更好的全局效率，所以整体上效率随着方案序号的增大而降低。效率的波动是由于网络节点之间的相互影响，增加某一个节点的效率可能会提高一部分节点之间的连接效率，同时降低另一部分节点间的连接效率，不同节点组合能产生不同的效果，这是由供应链网络的结构决定的。

算例的最佳方案效率值为32.65%，选取供应链网络中的5，6，4，9，13，11和12号节点，共计7个企业，结果并没有与之前的分析相悖，因为将资源分配到全部候选企业、即10个节点时，效率值达到32.32%，两者相差无几。由于网络节点的相互影响和作用，导致这7个节点的组合实现了效率最优，这为我们研究全局受损供应链的修复研究提供了思路。

3.3 节点受损供应链修复机制研究

取α=4，r=200，m=10，n=15，选择5号节点进行仿真。不同连边数下所有方案的平均效率见表2。随着方案所含边数的增多，平均供应链网络效率呈逐渐增大的趋势。总体上，修复更多的受损连边、恢复更多的业务往来，能够得到更好的网络效率。

对确定连边数下的各个方案进行具体分析，部分结果如图4。

随着方案序号的增大，供应链网络效率在轻微波动中呈阶梯状逐渐下降。因为候选边是按重要性的降序进行排列的，重要的连边相对集中在序号值较小的方案中，优先恢复它们的能力可以得到更好的全局效率。效率的波动是由于网络内部的相互影响，增加某一条连边的效率可能会提高一部分节点之间的连接效率，同时影响另一部分节点间的连接效率，不同的组合能产生不同的效果。

表2 不同连边数下方案的平均效率

Table 2 Average efficiency of the scheme under different link number

方案所含边数供应链网络平均效率/%1041.091142.051243.051344.041445.001545.91

图4 连边数为18时各方案的效率Fig.4 Efficiency of each scheme when the number of edges is 18

4 结论

1)基于企业间当量物流量和空间距离提出连边权重的计算方法，以BBV模型为基础，从有向加权复杂网络的角度建立供应链模型。

2)在连边权重的基础上提出连接阻力的概念，结合连接阻力对传统复杂网络效率公式进行改进，设计出供应链网络效率公式，作为供应链整体表现的评价指标。

3)分别对全局受损供应链和节点受损供应链的修复机制进行了研究，从整体趋势上看，将修复资源分配到更多的受损企业和业务能够取得更好的供应链网络效率，优先对重要性较高的企业和业务进行修复时也能有更好的效率表现，但是本文是从供应链网络的整体考虑效率，节点和连边之间相互影响，不同的组合会产生不同的结果，效率处于不断波动之中。

[1] 倪燕翎, 李海婴. 供应链风险管理与企业风险管理之比较[J]. 物流技术, 2004(10): 40-42. NI Yanling, LI Haiyin.Comparison of SC risk control with enterprise risk control[J]. Logistics Technology, 2004, 10: 40-42.

[2] 胡金环, 周启蕾. 供应链风险管理探究[J]. 价值工程, 2005, 3(9): 36-39. HU Jinhuan, ZHOU Qilei. On risk management in supply chain[J]. Value Engineering, 2005, 3(9): 36-39.

[3] 吴康迪. 台湾大地震对世界内存芯片市场的影响[J]. 海峡科技与产业, 2000(1): 4-5. WU Kangdi.The impact of Taiwan earthquake on the world memory chip market[J]. Technology and Industry Across The Strait, 2000(1): 4-5.

[4] Latour A. Trial by fire: A blaze in albuquerque sets off major crisis for cell-phone giants[J]. Wall Street Journal, 2001, 1 (29): 2001.

[5] 胡梦飞. 基于供应不确定的供应链中断风险管理研究[D]. 北京: 北京交通大学, 2011. HU Mengfei. The research on risk of supply chain disruption based on supply uncertainty[D]. Bejing: Beijing Jiaotong University, 2011.

[6] 刘纯霞, 舒彤, 汪寿阳, 等. 基于小世界网络的供应链中断风险传导路径研究[J]. 系统工程理论与实践, 2015,35(3): 608-615. LIU Chunxia, SHU Tong, WANG Shouyang, et al. Supply chain disruption risk conduction route based on the small world network[J]. Systems Engineering -Theory&Practice, 2015, 35(3): 608-615.

[7] 杨小雨. 供应链中断的修复研究[D]. 北京: 北京交通大学, 2012. YANG Xiaoyu.Research about restoration of supply chain disruption[D]. Beijing: Beijing Jiaotong University, 2012.

[8] Surana S. Supply-chinanetworks: A complex adaptive systems perspective[J]. International Journal of Production Research, 2005: 43(20): 4235-4265.

[9] Srinivas Talluri, Baker R C. A multi-phase mathematical programming approach for effective supply chain design[J]. European Journal of Operational Research, 2002(12): 544-558.

[10] Thadakamalla H P, Raghavan U N, Kumara S, et al. Survivability of multiagent-based supply networks: A topological perspective[J]. IEEE Intelligent Systems, 2004, 19 (5): 24-31.

[11] 杨光华, 李夏苗, 蔡鉴明. 区域物流网络结构关系分析与实证[J].铁道科学与工程学报, 2009, 6(4): 91-96. YANG Guanghua, LI Xiamiao, CAI Jianming.Structural relation analysis and relevant empirical of regional logistics network[J]. Journal of Railway Science and Engineering, 2009, 6(4): 91-96.

[12] 李刚. 基于复杂网络的供应链建模与性能分析研究[D]. 杭州: 浙江大学, 2012. LI Gang.Supply chain modeling and performance analysis based on complex network[D]. Hangzhou: Zhejiang University, 2012.

[13] 孟繁华. 基于复杂网络的供应链建模及其鲁棒性分析[D]. 北京: 华北电力大学, 2010. MENG Fanhua. Thesupply chain network modeling based on complex network and its robustness analysis [D]. Beijing: North China Electric Power University, 2010.

[14] Barrat A, Barthelemy M, Vespignani. A weighted evolving networks: coupling topology and weighted dynamics[J], Phys Rev Lett, 2004(92): 228-701.

[15] 罗宜美, 林强, 周刚, 等. 基于当量物流量的设备系统平面布置设计研究[J].机械设计, 2000, 11(11): 46-48. LUO Yimei, LIN Qiang, ZHOU Gang. A study on planar arrangement design of equipment system based on equivalent flow capacity of things[J]. Journal of Machine Design, 2000, 11(11): 46-48.

[16] 周艳菊, 邱莞华, 王宗润. 供应链风险管理研究进展的综述与分析[J]. 系统工程, 2006, 24(3): 1-7. ZHOU Yanju, QIU Wanhua, WANG Zongrun. Review and analysis on the research progress of supply chain risk management[J]. Systems Engineering, 2006, 24(3): 1-7.

[17] 邵鲁生, 秦绪伟. 面向供应节点失效的供应链应急策略研究[J]. 管理学报, 2013, 10(6): 913-918. SHAO Lusheng, QIN Xuwei. Emergency strategy for supply chain under supply node’s failure[J]. Chinese Journal of Management, 2013, 10(6): 913-918.

[18] 闫妍, 刘晓, 庄新田. 基于节点失效的弹性供应链应急管理策略[J]. 控制与决策, 2010, 25(1): 25-30. YAN Yan, LIU Xiao, ZHUANG Xintian. Resilient supply chain emergency management strategy based on node fails[J]. Control and Decision, 2010, 25(1): 25-30.

Research on supply chain repair mechanism based on directed weighted complex network

HE Heming, CHENG Yaorong

(School of Trafficand Transportation Engineering，Central South University，Changsha 410075，China)

In order to study the repair mechanism of damaged supply chain from the perspective of overall efficiency, the weight of the supply chain links was adjusted to simulate the damage of the supply chain, allocate limited repair resources, and find the optimal solution with supply chain network efficiency as the index. Logistics volume and spatial distance were combined to calculate the weight of links, and a directed weighted supply chain network model was established on the basis of BBV. The formula of the shortest path combined with connection resistance was improved, and the efficiency index of supply chain network was designed based on the average minimum cooperation resistance between nodes. Supply chain repair mechanism was studied from the global damage and the damage of one node, and the optimal efficiency scheme was found. Results show that due to the mutual influence existing between nodes and links, different combinations of nodes and links can produce different effects, while the restoration scheme has more global significance from the point of the efficiency of supply chain network.Key words：supply chain；network efficiency；complex network；BBV；repair mechanism

2016-01-07

成耀荣(1964-)，男，湖南湘潭人，教授，从事共同配送及物流系统规划研究；E-mail: yaorong@csu.edu.cn

F252

A

1672-7029(2016)11-2299-06