基于系统动力学的地铁客村站客流控制研究

郑雪梅，蒋熙

(北京交通大学 轨道交通控制与安全国家重点实验室，北京 100044)



基于系统动力学的地铁客村站客流控制研究

郑雪梅，蒋熙

(北京交通大学 轨道交通控制与安全国家重点实验室，北京 100044)

针对城市轨道交通系统高峰期间普遍存在的客流拥堵问题，以广州地铁客村站为研究对象，研究基于系统动力学的车站客流拥堵控制方法。通过构建客村站的系统动力学模型对车站现状进行仿真实验，以推演客流在站内设施上的分布及其动态变化过程，进而明确当前客流拥堵的关键位置及拥堵成因。在此基础上，设计客流拥堵的控制方案，并通过一系列仿真实验对控制方案进行优选和验证以确定最终的客流控制方案。研究结果表明：基于“流”的系统动力学建模与仿真在制定客流拥堵控制方案方面的有效性。

城市轨道交通；客流控制；系统动力学；关键位置

目前，高峰期客流拥堵已成为许多大型城市轨道交通系统的运营常态，如何应对此问题是运营管理者及许多学者所关注的重点。当短期内运输能力提升非常有限的情况下，在必要的时候对拥堵车站实施客流组织与控制是保证乘客出行安全及提高运输效率的重要手段。而实施有效客流拥堵控制的关键在于，根据车站设施、客流特性、客流拥堵状况及演化规律，制定合理的客流控制方案，即设定客流控制的关键设备及相应的控制参数[1-2]。鉴于轨道交通系统车站运营状态所具有的复杂动态特性，相对一般的数学解析方法，仿真建模可以更好地揭示客流拥堵的发生及演化规律，从而在拥堵客流控制问题上发挥其优势。

目前国内许多学者利用仿真建模的方法对轨道交通车站内客流问题进行研究。胡明伟等[3-6]从乘客个体角度分别研究了车站客流微观仿真模型的构建及相应的车站客流组织问题。薛霏等[7-9]则利用系统动力学方法从乘客群体，即“流”的角度建立仿真模型并进行车站运营分析与计算。相比微观仿真模型，基于“流”的系统动力学方法既能够减少建模的工作量及复杂性，又能简单直观地体现客流组织措施带来的影响效果，因此，本文利用系统动力学方法进行建模与仿真，并在此基础上制定合理的客流控制方案。

1 基于系统动力学的客流控制方案制定方法

系统动力学是一门通过分析研究信息反馈系统来认识和解决系统问题、沟通自然科学与社会科学的边缘学科，为系统科学的一个分支。它可通过建立研究对象的模型进行仿真以研究系统状态动态变化过程，并通过改变模型中相关参数或变量来试验各种方案的实施效果，进而寻找解决问题的最佳方案[10-11]。

把握客流拥堵的形成及演化规律是实施客流拥堵控制的前提，本文运用系统动力学方法构建车站模型，以推演客流在车站内设施上的分布及其动态变化过程。基于该模型，针对车站现状进行仿真实验，可明确目前车站产生客流拥堵的关键位置及拥堵形成的原因；在此基础上，进行客流控制方案的设计，形成一系列备选方案；再将其作为系统动力学模型的输入要素，针对不同方案进行相应场景下的仿真试验；最后，根据仿真运行结果数据对方案实施效果进行分析比较，优选出合理的客流控制方案。由此，本文运用系统动力学模型制定车站拥堵控制方案的步骤如图1所示。

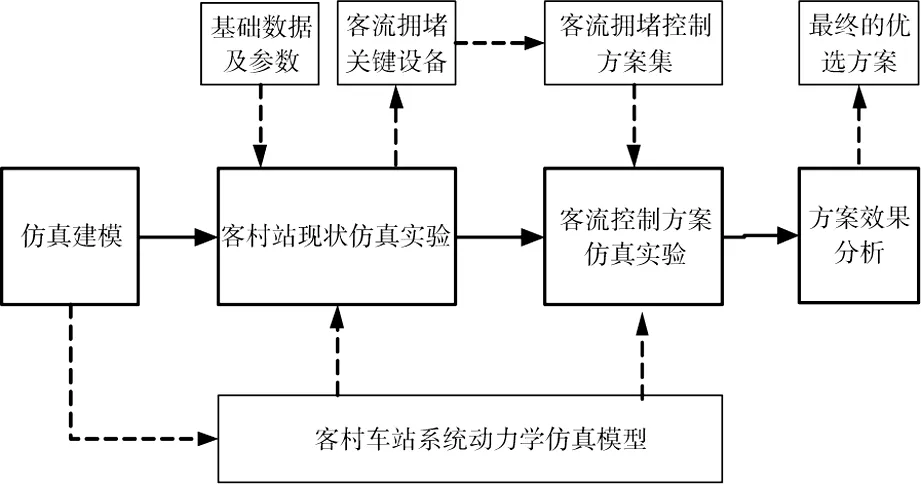
图1 客流控制方案制定步骤Fig.1 Step of flow control scheme

2 城市轨道交通车站客流系统动力学建模

客村站早高峰期间存在客流拥堵的问题，本文以客村站为研究对象，根据站内设备设施布局、车站客流与乘客活动、列车到发计划及其相互关系，构建客村车站的系统动力学模型，用于研究客村站合理的客流控制方案

2.1 车站建模要素

城市轨道交通车站是乘客、基础设施、运营组织三种要素相互作用的复杂系统，车站系统动力学模型需描述车站在这3种要素相互作用下系统的运营状况及变化过程。

1)车站设施

客村站内部对乘客活动及拥堵形成影响较大的设施主要包括进出站口、站厅、闸机、站台等，临时售票点和自动售票机等设施对客流拥堵的影响较小[13]。本文选取对客流影响较大的设施，并根据其布局和客流流线构建客村站的车站拓扑结构，如图2所示。

根据站内设备的作用，将其分为如下类型：

①承载设备：主要包括站厅、站台、换乘平台，这些设备作为供乘客走停的容纳区域，是体现车站整体客流分布的核心区域。

②连接设备：主要包括进站出站设施、通道、自动扶梯、楼梯等，作为为供乘客走行的流通区域，这些设备影响了客流在承载设备上的进、出与停留。

③衔接节点：包括安检、闸机及其他乘客驻足区，这些设备为上述各设备的分隔点且可影响乘客流线或速度。

图2 车站拓扑结构Fig.2 Station topology

2)客流

在运营时段内，按照一定到达规律进站的乘客在站内各项设施上的活动决定了车站客流的时空分布及动态变化[14-15]。由此可知，客流量、客流构成、客流到达参数、客流流向与流线等要素需在模型中进行描述。其中，客村站的乘客流线分为进站流线、出站流线及换乘流线三种。而客流在各设施上分布数量及变化则是需要由系统动力学模型输出的仿真数据。

3)运营组织

以客流组织措施的形式体现出来的运营组织是影响乘客在站行为与客流分布的另一关键要素。尤其是在发生拥堵的情况下，运营管理者经常会采取某些限流措施控制某些设施上的客流流动及数量，以保证车站运营安全及效率。在模型中，其可表现为某些参数的设置，通过控制客流数量或流动速率，以此达到客流控制的目的。

2.2 系统动力学模型构建

经调查发现，客村站进、出站口目前尚未出现客流拥挤，乘客进出站为自由走行状态。本文将站厅、站台、换乘平台这些承载设备上的客流作为积累变量，进出站口、闸机、楼梯、自动扶梯、通道等连接设备上的客流作为速率变量，并按照列车运行图设置客村站的列车到发时间及行车间隔。

对车站内不同设备上的客流进行因果分析后，构建了车站客流的因果关系图如图3所示。在此基础上，建立客村站的系统流图，如图4所示。

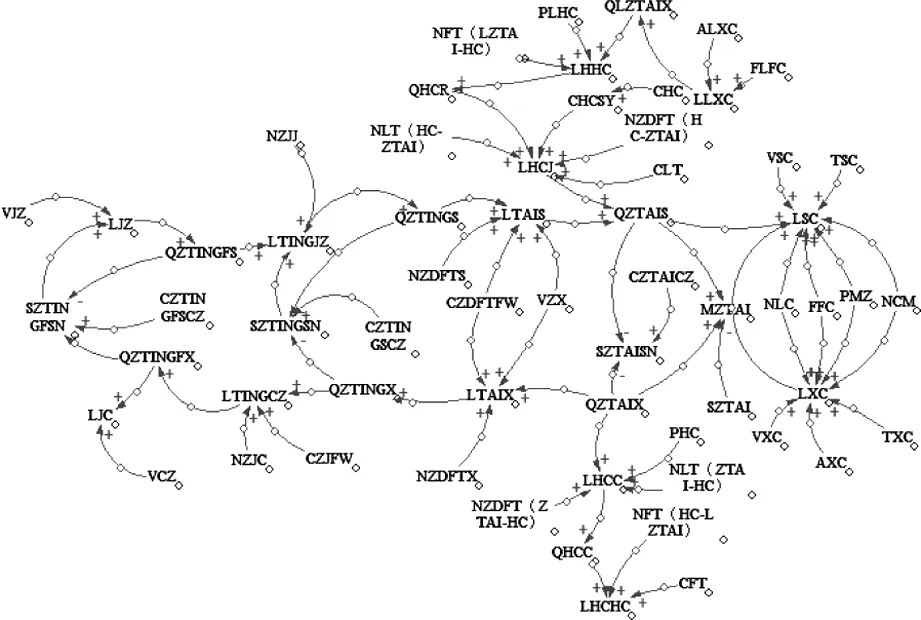
图3 因果关系图Fig.3 Casual diagram

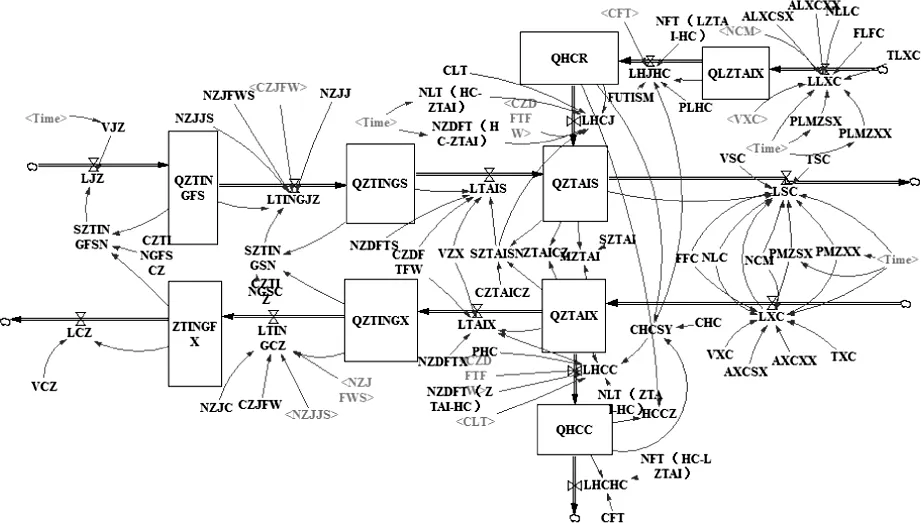
图4 系统流图Fig.4 System flow diagram

模型中定义的相关变量，如表1：

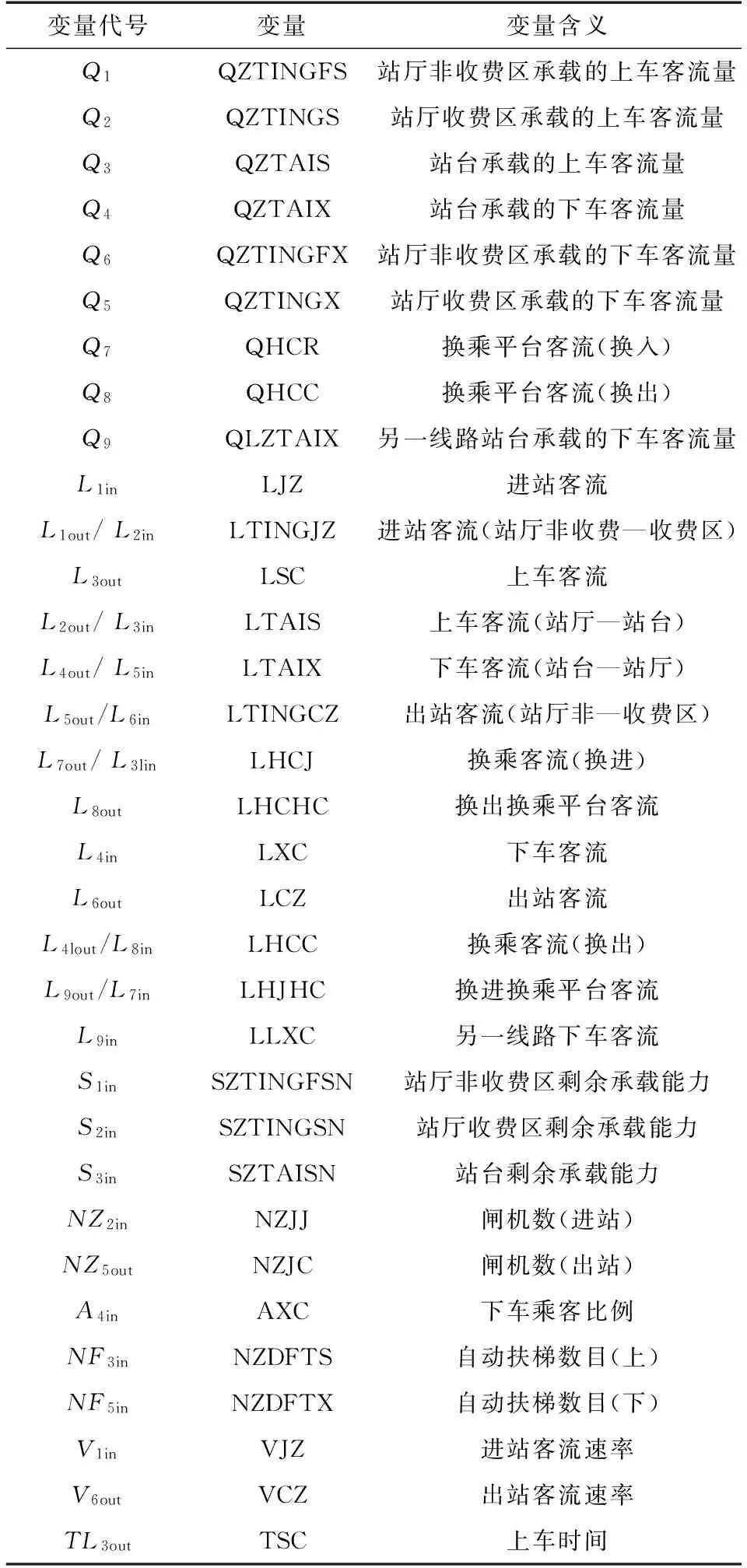
表1 变量说明表

续表1

此外，还包括：楼梯通过能力(CL)、扶梯通过能力(CF)、客流走行速度(V)、客流上车速度(VSC)、客流下车速度(VSC)、列车车门数(NLC)、闸机服务能力(CZJ)、设备承载能力(CHC、CZTINGSCZ、CZTINGFCZ、CZTAICZ)等常量。

依据车站内各设备上客流动态变化的逻辑关系与数学关系，建立系统动力学方程如下：

1)积累变量计算方程

Qi=∫[Liin(t)-Liout(t)]dt, i=1,2…9

(1)

式中：Qi为车站i设备上在t时刻的客流量；Liin(t)为在t时刻客流流入i设备的速率；Liout(t)为在t时刻客流流出i设备的速率。

2)速率变量计算方程

Liin(t)=MIN(MIN(V,NFiin*CF+

NLiin*CL,Qi*Pin),Siin),

i=1,2,5…8,

(2)

Liin(t)=IF THEN ELSE(MODULO(TIME,

Fiin)=0,MIN(Viinor out*TLiinor out,

Aiinor out*Piinor out*Diinor out),0),

i=3,4,9

(3)

式中：Liin(t)为在t时刻客流流入的i设备上速率；其它为与之相关的辅助变量及常量。

3)辅助变量的计算方程：

S1in=CS1in-Q1-Q6

(4)

S2in=CS2in-Q2-Q5

(5)

S3in=CS3in-Q3-Q4

(6)

S8in=CS8in-Q7-Q8

(7)

式中：Siin为在t时刻客流流入的i设备上剩余承载能力；CSiin为车站i设备的承载能力。

3 仿真实验及分析

本文选取6:15-9:00时段作为仿真的起止时间，将已知参数及调查数据输入模型中进行仿真试验，得到系统动力学模型中各变量随时间推进的动态变化数值。仿真结束后对仿真结果进行分析并据此制定客流控制方案。

3.1 输入参数及调查数据

模型依据《地铁设计规范》对乘客参数(乘客走行速度)、设备参数(闸机服务能力、扶梯通行能力等)等进行设置[12]。据调查设定客村站3号线行车间隔为3 min，停站时分为60 s；8号线行车间隔为4 min，停站时分为45 s。客村站早高峰3号线番禺广场方向的下车率设为35%，3号线天河客运站方向的下车率设为50%，8号线凤凰新村方向的下车率设为30%，8号线万胜围方向的下车率设为50%，将上述数据输入模型中。

3.2 关键控制设备的确定

利用Vensim仿真平台，利用构建的系统动力学仿真模型，对客村站的现状进行仿真，得到客流在设备上随时间动态变化的数据，并依照关键设备的选择依据对输出数据进行分析。

1)关键设备的选择依据

关键设备是以设备上客流量是否满足安全运营的标准为选择依据。在车站系统内，为了保证运营安全，站台最大安全承载能力为其最大承载能力乘以安全系数γ，其他承载客流设备的最大安全承载能力为其最大承载能力，在本文中安全系数γ取75%。则三号线站台最大安全承载能力=1 380人，八号线站台最大安全承载能力=2 028人。

2)结果分析

对仿真结果分析后，可知站厅、8号线站台未发生客流拥堵，换乘平台客流消散较快且不会影响安全运营，因此本文将客村站3号线站台作为关键设备。在运营时段内，3号线站台承载客流量随时间的动态变化情况如图5所示：

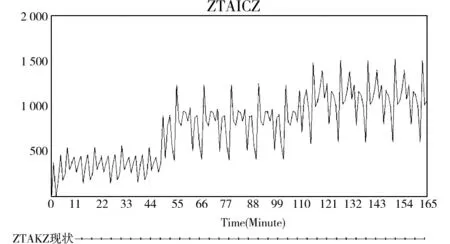
图5 站台承载客流量Fig.5 Curve of passengers on the platform

由图5可见，在仿真的第115 min，3号线站台客流量为1 482人，且随时间推移，站台客流量大于安全承载人数的时间逐渐增加，为保证其安全需对流入客流进行控制。

3.3 客流控制方案设计与仿真实验

经调查，可知3号线站台上的客流主要源于下车客流、换乘客流及上车客流。在不改变列车运行及车站设备布局的情况下，为达到控制3号线站台客流量的目的，可对进站客流及换乘客流进行控制。本文按照10%，20%，30%和35%的比例分别对进站和换乘到3号线站台的客流进行限流，通过改变控制参数设计一系列限流方案，将其输入模型中进行仿真实验，结果如表2所示。

表2 站台最大客流量

由上表，可知换乘限流35%时站台客流量符合安全运营的标准，而单独进行进站限流的各方案均未达到标准要求。由此可知在同等限流条件下，换乘限流的效果优于进站限流。进一步，考虑进站与换乘同时限流的方式，设计了相应的客流控制方案集。对比限流方案结果后，得知实施进站限流25%与换乘限流30%时3号线站台的最大承载客流量为1 379人，满足限流最小且安全运营的标准，故将其作为最终的限流方案。站台流量限流前后对比如图6所示:

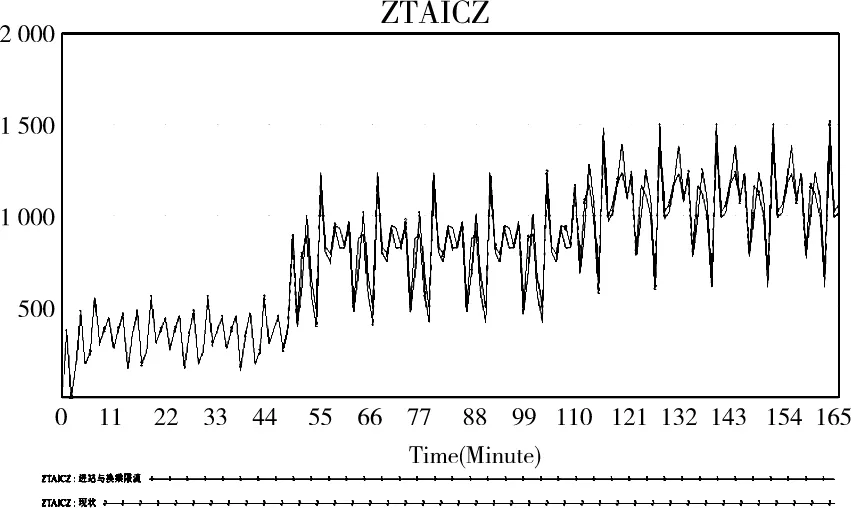
图6 限流前后客流量对比Fig.6 Comparison curve of limiting traffic before and after

结合实际情况，为达到最终客流控制方案的效果，可采取如下客流组织措施：

1)降低进站客流流入3号线站台的速率，可采取站厅限流。

2)降低换乘客流流入3号线站台的速率，可采取限制换乘客流经换乘平台去往3号线站台，引导或者强制乘客绕行至站厅去往3号线站台。

4 结论

1)本文运用系统动力学方法建立车站模型并仿真试验，依据仿真结果确定车站当前产生客流拥堵的关键位置及拥堵形成的原因，在一定程度上明确了站内当前存在的运营组织问题，并据此制定相应的客流控制方案。

2)模型还可设置多种限流方案，以解决现实场景下无法进行客流控制试验以进行控流效果对比的问题。结果表明基于“流”的系统动力学建模与仿真在应对客流组织的问题方面具有一定的可行性及有效性。

[1] Nuzzolo A, Crisalli U, Rosati L. A schedule-based assignment model with explicit capacity constraints for congested transit networks[J]. Transportation Research Part C: Emerging Technologies, 2012,20(1): 16-33.

[2] Jiang C S, Yuan F, Chow WK. Effect of varying two key parameters in simulating evacuation for subway stations in China[J]. Safety Science 2010,48(4):445-451

[3] 胡明伟，史其信.城市轨道交通车站客流组织仿真和评价[J].交通信息与安全,2009,3(27):39-42. HU Mingwei, SHI Qixin. Urban rail transit station passenger flow organization simulation and evaluation [J]. Computer and Communications, 2009,3(27):39-42.

[4] 夏菁.城市轨道交通枢纽站客流组织优化与仿真[D].兰州：兰州交通大学,2013. XIA Jing.The optimization and simulation of passenger flow organization in mass rapid transit hubs[D]. Lanzhou: Lanzhou Jiaotong University,2013

[5] 杨梅,徐瑞华.城市轨道交通换乘站大客流组织的仿真[J].城市轨道交通研究,2011,9(9):48-51. YANG Mei, XU Ruihua. Simulation of large-scale pedestrian organization at urban rail transfer station [J].Urban Mass Transit,2011,9(9::48-51.

[6] 李洪旭，李海鹰，樊校，等.基于Anylogic的地铁车站集散能力仿真分析评估[J].轨道交通信息系统,2012,8(21):48-55. LI Hongxu, LI Haiying, FAN Xiao, et al．Anylogic-based simulation analysis and evaluation of subway stations assemble capacity [J].Railway Computer Application, 2012,8(21):48-55.

[7] 薛霏,方卫宁，郭北苑.基于系统动力学的轨道交通车站客流演变算法[J].铁道学报, 2014,2(36):1-10. XUE Fei, FANG Weining, GUO Beiyuan. Rail transit station passenger flow evolution algorithm based onsystem dynamics [J]. Journal of the China Railway Society, 2014,2(36):1-10.

[8] 贺英松.轨道交通车站乘客流量控制措施分析与研究[D].北京：北京交通大学,2013. HE Yingsong. Analysis research on the control measures of passenger flow in transit stations[D]. Beijing: Beijing Jiaotong University,2013.

[9] 康亚舒.城市轨道交通车站客流控制方案的研究[D].北京：北京交通大学,2014.. KANG Yashu. Research on passenger flow volume control plan for urban for urban rail transit station[D]. Beijing: Beijing Jiaotong University,2014

[10] 王其藩.系统动力学[M].上海:上海财经大学出版，2009. WANG Qifan. System dynamics[M]. Shanghai: Shanghai University of Finance and Economics Press，2009.

[11] 何建伟.基于系统动力学的城市交通流网络管控系统分析与建模[D].天津：河北工业大学,2009. HE Jianwei. An analysis and modeling on urban traffic management and control systems on the basis of systems dynamics[D]. Tianjin: Hebei University of Technonly,2009.

[12] GB 50157—2013，地铁设计规范[S]. GB 50157—2013， The specification of metro design[S].

[13] 邵一琨.基于系统动力学的地铁车站客流量影响因素分析[J].科技创新与应用,2014,11(11):241-241. SHAO Yikun. Analysis of metro station passenger flow influence factorsbased on system dynamics[J]. Technology Innovation and Application, 2014,11(11):241-241.

[14] Zhao Zhang, Brian olshon, Vinayak V. Dixit. Integration of a cell transmission model and macroscopicfundamental diagram: Network aggregation for dynamic trafficmodels.[J].Transportation Research Part C,2015:298-309.

[15] Helbing, D. Self-organized pedestrian crowd dynamics: experiments, simulations, and design solutions[J]. Transportation Science, 2005(39):1-24.

[16] 胡清梅, 轨道交通车站客流承载能力的评估与仿真研究[D]. 北京：北京交通大学,2011. HU Qingmei. Passenger carrying capacity evaluation and simulation of rail transit station[D]. Beijing: Beijing Jiaotong University,2011.

The study of passenger flow control at kecun station of urban rail transitbased on system dynamics

ZHENG Xuemei，JIANG Xi

(State Key Laboratory of Rail Traffic Control and Safety, Beijing Jiaotong University, Beijing 100044,China)

For the common passenger flow congestion problems in urban rail transit system during peak periods, this study took the Kecun station of Guangzhou subway as an example to investigate for this station passenger flow congestion control methods based on system dynamics. The system dynamics model of Kecun station was developed to simulate station status and deduce the passenger flow distribution. The dynamic changes in the facilities of the station and the key causes of the current position and the traffic congestion were identified. According to simulation results, the passengers flow congestion control plan was designed, and then the final passenger control program was determined through the selection and verified through a series of simulations. The results show that simulation modeling based on the “flow” has a certain validity in the study of traffic congestion control program.

urban rail transit; traffic control; system dynamics; key positions

2016-02-11

国家重点实验室自主课题资助项目(RCS2015ZZ002)；北京科技计划专项资助项目(2141106004414106)

蒋熙(1971-)，女，四川江油人，副教授，博士，从事运输组织理论与技术研究；xijiang@bjtu.edu.cn

U121

A

1672-7029(2016)11-2284-06