基于Bloch球面坐标的改进量子遗传算法及其应用

李家才，韩锟，鲍天哲

(中南大学 交通运输工程学院，湖南 长沙 410075)



基于Bloch球面坐标的改进量子遗传算法及其应用

李家才，韩锟，鲍天哲

(中南大学 交通运输工程学院，湖南 长沙 410075)

为解决量子遗传算法(QGA)用于连续多峰函数优化易陷入局部极值的问题, 提出一种基于Bloch球面坐标的改进量子遗传算法(GLBQGA)：该算法通过引入新的全局-局部变异算子，在保证全局特性基础上加入局部搜索机制，使算法在搜索到全局最优近似解之后能通过局部邻域搜索收敛到全局最优精确解；算法还进一步优化量子转角取值方案，在保证搜索空间不变的同时提高搜索效率。在机车二系支承载荷均匀性分配优化调整及短时交通流多步预测中的应用表明，GLBQGA有效克服了QGA早熟收敛的问题，在不显著增加搜索时间的前提下提高了求解精度。

Bloch球面坐标；量子遗传算法；调簧；交通流预测

量子遗传算法((Quantum Genetic Algorithm，QGA)是一种用量子相位表示种群元素的概率优化算法[1]，它将量子的态矢量表达引入遗传编码，使得一条染色体可以表达多个态的叠加，并利用量子逻辑门实现染色体的演化[2]。由于单个染色体多样性特征更好[3]，该算法对种群规模的需求明显降低[4]，算法具有种群规模小、收敛速度快、全局搜索能力强[5-6]等优点，近年来成为优化领域的研究热点。但测试发现QGA用于连续函数优化时易出现早熟收敛，且易陷入局部极值[7]，为克服这一缺陷，学者们提出了大量的改进量子遗传算法，其中基于Bloch球面坐标的量子遗传算法(Bloch quantum genetic algorithm，BQGA)[8]因使用三链基因编码且没有选择、交叉和复制运算，获得了搜索能力和优化效率的综合提高。但BQGA采用量子位沿Bloch球面较大幅度的旋转作为变异操作，有可能使算法越过全局最优解或产生振荡，且BQGA在寻优过程中搜索整个Bloch球面[6]，无疑降低了搜索效率。因此，本文提出一种引入新的全局-局部变异算子的Bloch球面坐标量子遗传算法(Global-Local Bloch quantum genetic algorithm, GLBQGA)，以期改善BQGA算法的鲁棒性、加快算法收敛速度，且提高算法求解精度。将GLBQGA算法应用于机车二系支承载荷均匀性分配优化调整及短时交通流超前多步预测，应用结果表明了GLBQGA算法的有效性。

1 GLBQGA算法基本思想

GLBQGA在文献[8]提出的BQGA算法基础上进行以下改进：

1)压缩转角参数取值范围：将量子比特角度参数φ的取值区间由(0,2π)缩小到(0,3π/2)，可在保证搜索空间不变的同时提高搜索效率。

2)引入全局-局部变异算子：在变异操作中引入全局-局部变异算子取代量子非门，通过改变算子的全局-局部变异权重系数控制搜索过程中全局变异和局部变异的比重，在算法前期以全局变异为主，使量子位沿Bloch球面大幅度旋转，充分利用整个解空间的信息进行全局搜索，克服早熟；而在算法后期以局部变异为主，变异操作仅在个体所在邻域内进行，充分利用已在最优解附近分布个体所隐含的局部信息，提高算法的局部搜索能力，以找到全局最优精确解。

3)引入自适应操作：算法搜索过程中自适应改变转角步长和变异率，以改善收敛特性。

2 GLBQGA算法设计

2.1 编码及解空间变换

在GLBQGA里，用量子位的Bloch球面坐标作为染色体编码。

在图1所示的Bloch球面坐标中，任何量子位都与球面上的一点对应[6]，而通过量子位的角度参数φ和θ可以确定球面上的任一点，因此量子位可用球面坐标表示为：

(1)

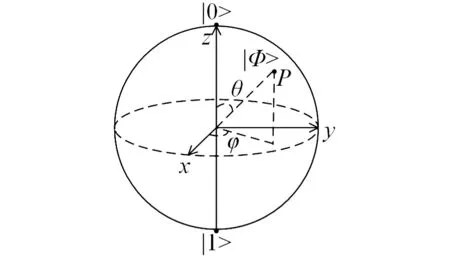
图1 量子位的Bloch 球面表示Fig.1 Bloch sphere representation of a qubit

将pi定义为群体里的第i条染色体，其编码如图2所示：

图2 染色体编码Fig.2 Chromosome coding

图2中，i=1,2,…Nind，Nind为种群规模，n为量子位数目。将量子位的三个坐标看作三条并列的基因链[7]，每条基因链代表一组优化解，则每条染色体含有以下三组优化解：

(2)

采用线性变换实现定义在单位空间In=[-1,1]n内的染色体向定义在优化问题解空间内的优化解之间的变换，公式为：

(3)

式中，j=1,2,…n；bj和aj为优化问题解空间的最大值和最小值。

2.2 搜索区域定义

传统Bloch球面量子遗传算法通常会对整个球面进行搜索[8]，即转角参数φij和θij的取值范围分别为(0,2π)和(0,π)。这样虽然扩充了最优解的个数，但也相应扩大了算法的搜索范围。文献[9]通过对连续问题可行解与Bloch球面对应关系的研究发现，合理设置转角参数的取值范围可在保证实际搜索空间不变的前提下减少搜索时间。事实上，由图3可知，当转角φij的取值范围压缩到(0,3π/2)时，sinφ与cosφ仍然覆盖(-1,1)的解空间，此时量子比特同样可以遍历整个Bloch球面。基于此，本文将φij和θij的取值范围重新定义为(0,3π/2)和(0,π)，在保障搜索空间的同时进一步提高算法效率。

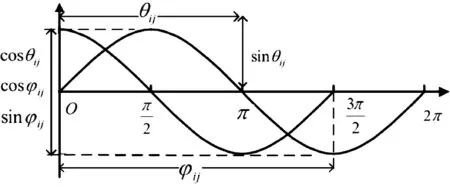
图3 φij和θij的取值范围Fig.3 Reasonable ranges of parameters φijandθij

2.3 最优染色体选择

每条染色体有三个基因链，对应三个目标函数值，应以最好的基因链代表该染色体，故按照式(4)确定该染色体的适应度：

(4)

选择种群中适应度值最大的染色体为当代最优染色体，其三个基因链中目标函数值最小者为当代最优基因链。

2.4 量子染色体的更新

区别于传统遗传算法，BQGA中，量子染色体的更新一般是通过旋转门改变量子相位来实现的。它可以使当前每个染色体向当代最优染色体靠近，并在逼近过程中产生更加优良的个体，从而完成种群进化。文献[9]提出了一种较为有效的量子旋转门，与原量子相位相乘后可使φ和θ分别旋转Δφ和Δθ，其形式为:

U=

(5)

关于转角方向，文献[9]也给出了相应的规则，可以通过当前染色体与最优染色体量三个量子位坐标的代数运算进行判断。对于转角大小，本文采用转角值随迭代步长随代数单调下降的调整策略，使之具有一定的自适应性，具体为:

(6)

其中φ0的取值范围是(0.005π,0.1π)；θ0=k0φ0，k0∈(0,1)。

2.5 全局-局部变异操作

传统的量子遗传算法常采用量子非门作为变异算子，依据变异概率随机选择每条染色体的若干量子位施加变异。该方法实际是使量子位沿Bloch球面进行较大幅度的旋转，在算法前期可充分利用整个解空间的信息，有利于克服早熟。但在算法迭代后期，特别是算法已收敛至全局最优解附近时，这种量子位沿Bloch球面较大幅度旋转的变异操作不能对搜索空间的细节进行局部搜索，可能使搜索越过全局最优解，甚至使搜索过程在全局最优解附近产生振荡而不能找到全局最优精确解。在这种情况下，局部搜索显得格外重要，此时应充分利用个体所隐含的局部信息，提高算法的局部搜索能力，使算法收敛到全局最优精确解。

基于此，借鉴蚁群算法中的局部搜索机制[10]，本文构造了如下变异算子：

(7)

其中λ为全局-局部变异权重系数，λ∈(0,1)。该变异算子具有如下特征：

1)算子兼具全局和局部搜索特征，全局搜索和局部搜索力度由权重系数λ控制，λ越大，越突出全局搜索，当λ取1时该算子退化为标准的量子非门变异操作；

2)可通过改变权重系数λ控制 GLBQGA搜索过程中全局变异和局部变异的比重：在算法前期，以全局变异为主，λ取接近1的较大值，使量子位沿Bloch球面大幅度旋转，充分利用整个解空间的信息进行全局搜索，克服早熟；而在算法后期以局部变异为主，λ取接近0的较小值，使变异操作仅在个体所在邻域内进行，充分利用已在最优解附近分布个体所隐含的局部信息，提高算法的局部搜索能力，以避免算法振荡，提高算法精度。

对于很多优化问题，特别是单峰性比较明显的目标函数，迭代后期的种群常常集中分布在最优解附近，局部搜索显得格外重要。此时GLBQGA算法中的局部搜索策略更有助于找到目标函数的全局最优精确解。

对应于之前采用的自适应策略，变异概率Pm的取值公式为：

(8)

其中变异参数Pm0∈(0.01,0.1)。

2.6 精英保留机制

同传统遗传算法一样，精英保留机制可以使得种群不会退化，进而保证GLBQGA算法在有限迭代内以全概率收敛，具体策略为：

1)每一代最差染色体由这一代的最优染色体替代；

2)每一代最优染色体与历史最优染色体比较，若好于后者则将其替换，否则被其替换。

2.7 算法流程

步骤1：初始化各参数：设置种群规模Nind，迭代次数Gen，转角步长参数φ0、k0、全局-局部变异的权重系数λ和变异概率Pm；

步骤2：生成初始种群，结合具体优化问题利用式(3)进行解空间变换，依据式(4)计算各染色体适应度，并将其最优染色体和最优基因链作为历史最优染色体和基因链；

步骤3：利用式(6)中的量子旋转门更新染色体，利用式(8)中的全局-局部变异算子完成变异，得到新种群；

步骤4：进行解空间变换，计算各染色体适应度；

步骤5：执行精英保留机制；

步骤6：判断迭代次数是否达到设定值，若是则结束迭代，输出历史最优基因链在解空间的自变量值和目标函数值；若否则转步骤3。

3 GLBQGA算法在机车二系支承载荷调整中的应用

机车轮(轴)重分配的均匀性直接影响到机车牵引粘着、制动和动力学性能[11]。具有两系悬挂结构的机车，其二系支承载荷分布状态是影响机车轮轴重量分配的重要因素，将其视为刚性车体与多个支承弹簧构成的超静定空间力学系统，通过优化算法对二系支承载荷进行分配调整是改善轮(轴)重分配均匀性的有效途径。

3.1 机车二系支承载荷优化分配的数学模型

针对机车二系支承载荷调整优化问题，文献[11-14]构建了相应的优化模型，比较常用的形式为：

(9)

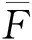
3.2 GLBQGA算法的应用及结果

二系支承载荷调整优化问题的编码及解空间变换公式为:

(10)

其中j=1,2,…,n，n表示量子位数，等于机车二系支承点的数量。

运用本文提出的GLBQGA算法对国产HXD1B型电力机车车体实车数据进行仿真调簧实验，算法参数选择如下：设置种群规模Nind=20，迭代次数Gen=200，转角步长φ0=0.1π，参数k0=0.5，全局-局部变异的权重系数在前120代取λ=1，后80代取λ=0.1，变异概率Pm=0.05，最大加垫量ΔHmax=7 mm。仿真结果如表1所示。

表1 HXD1B型机车初始二系载荷分布及优化结果

Table 1 Initial distribution and optimization results of secondary spring load of locomotive HXD1B

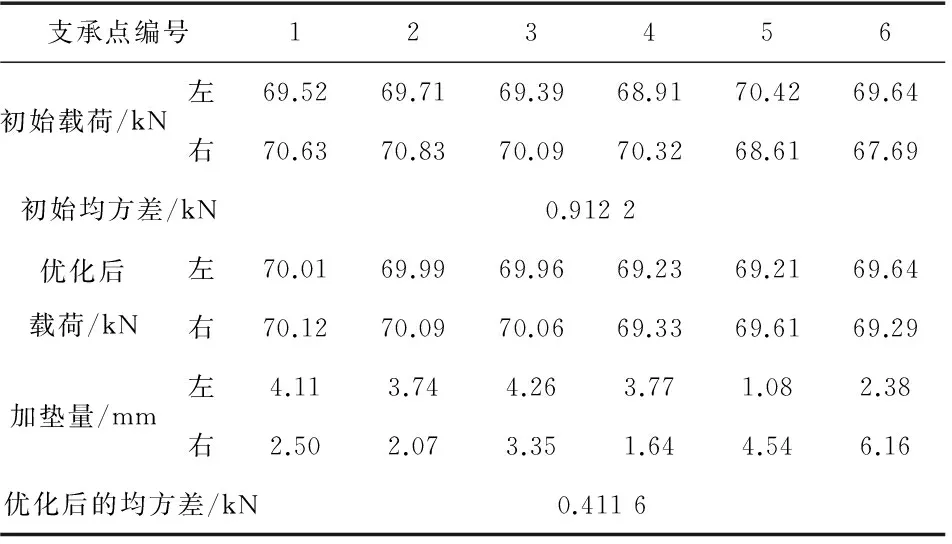
支承点编号123456初始载荷/kN左69.5269.7169.3968.9170.4269.64右70.6370.8370.0970.3268.6167.69初始均方差/kN0.9122优化后载荷/kN左70.0169.9969.9669.2369.2169.64右70.1270.0970.0669.3369.6169.29加垫量/mm左4.113.744.263.771.082.38右2.502.073.351.644.546.16优化后的均方差/kN0.4116

由表1可知，利用GLBQGA算法求解出的最优加垫序列对二系支承载荷进行数值仿真，载荷均方差由初始的0.912 2 kN下降至0.411 6 kN。通过机车车体称重调簧试验台[14]测试可知，该加垫序列显著优化了二系载荷分布。

为进一步验证该算法在全局搜索上的优势，将GLBQGA算法与文献[11]提出的标准遗传算法进行比较，后者的有效性在机车二系支承载荷调整中已得到广泛验证[11-14]。由于GLBQGA中每个染色体含有三条基因链，而每条基因链实际相当于标准遗传算法中的一个个体，因此后者的种群规模为60，迭代次数为200，其余参数的取值保持不变。两种算法在200次迭代中的收敛曲线如图4所示。

图4 GA与GLBQGA的迭代曲线Fig.4 Iterative curves of GA and GLBQGA

由图4可知：

1)标准遗传算法在30代左右即完成收敛，而GLBQGA算法在50代以后仍有显著的进化，在一定程度上克服了遗传算法早熟的弱点；

2)相同种群规模下，后者的搜索结果明显好于前者，且通过算法分析可知时间复杂度基本相似，说明GLBQGA算法有着更为强大的搜索全局最优精确解的能力，而这种求解精度的提高与算法迭代后期的局部搜索机制密切相关。

4 基于GLBQGA算法的短期交通流多步预测模型

交通诱导可以有效地改善城市交通拥挤，而实现城市交通诱导关键技术是对道路交通状况的实时预测。从动态规划的角度来说，多步预测相比于单步预测更为重要，但预测难度也更高。现有的多步预测模型主要是基于循环一步外推法实现多步预测[16]，即在单步预测基础上，将上一步预测的结果作为下一步预测的初始条件输入，通过多次递推过程实现对特定步数的预测。然而每一步的预测值中均携带有误差，递推过程不可避免地会产生误差放大效应，特别是一步预测已有较大误差时，递推后的多步预测可能会出现严重偏差。

考虑到短时交通流是一种前后关联性较强的随机过程，提出了一种基于GLBQGA算法的多步预测模型。该模型利用GLBQGA算法良好的学习能力，构建了当前时刻流量Xt与之前几步时刻的流量Xt-n、Xt-(n+1)、Xt-(n+2)… (t为当前时刻，n为预测步长)之间的函数关系，并将所得规律外推实现多步预测，从而避开了传统算法在递推过程中产生的误差累计效应。

4.1 多步预测模型的构建

4.1.1 模型基本结构

时间序列预测法在交通流预测领域有着广泛的应用，该模型结构简单，在数据充分的情况下有较高的预测精度[17]，是很多改进多步预测算法的模型基础[18-19]，且取得了良好的预测效果。参考该设计思路，本文采用AR模型为基本模型结构，将实测数据序列拟合成一个线性参数模型，如式(11)所示：

(11)

4.1.2 编码及解空间变换

根据交通流特性，GLBQGA算法的染色体在解空间变换后适宜采用[0,1]区间内的有序实数编码方式，具体的变换公式为：

(12)

由上式可得变换后的基因链：

(13)

4.1.3 目标函数设计

结合式(11)，对于每一代进化中的基因链，建立如下目标函数：

(14)

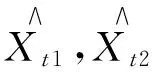
4.2 实验结果与分析

笔者对长沙市湘府路某路段由西向东方向的机动车流量进行了视频采集，每5 min统计一组，共100组，其中80组用于建模，20组用于预测。为了评价预测效果，选取平均绝对百分比误差(MAPE)作为评价指标，计算公式为：

(15)

AR模型建模的主要步骤包括时间序列预处理、模型定阶、模型参数估计与超前预测计算等。预处理采用一阶差分使其相对平稳化；模型定阶选择FPE(最小最终预报误差)准则，经计算判断最优拟合模型为AR(8)；参数估计选择较为成熟、计算简单可靠的矩估计法[20]。对AR(8)模型进行差分逆运算，可得超前一步预测模型：

0.196Xt-3…-0.049Xt-8

(16)

依据传统多步预测模型的建模思路，将超前一步的预测结果用于超前两步预测中，再将预测值用于超前三步预测，以此类推实现超前任意步数的预测，例如AR超前3步预测模型，则需要代入超前一步和超前两步的值，如式(17)所示：

0.196Xt-1…-0.049Xt-6

(17)

参考AR模型，本文多步预测基础模型采用AR(8)，如超前三步预测时，n=8，m=3，则超前三步预测模型如式(18)所示：

(18)

将式(18)和式(14)结合，构建GLBQGA算法的目标函数，其它参数设定与3.2节一致。读取前80个样本进行AR(8)模型参数拟合，对后20个样本进行预测，AR(8)模型和基于GLBQGA算法优化的AR(8)模型超前三步预测曲线分别如图5和图6所示。

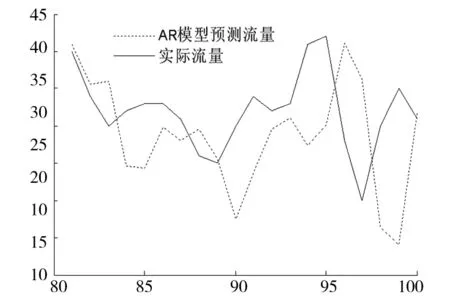
图5 AR(8)模型超前三步预测曲线Fig.5 Three-step ahead forecasting results of AR(8) model

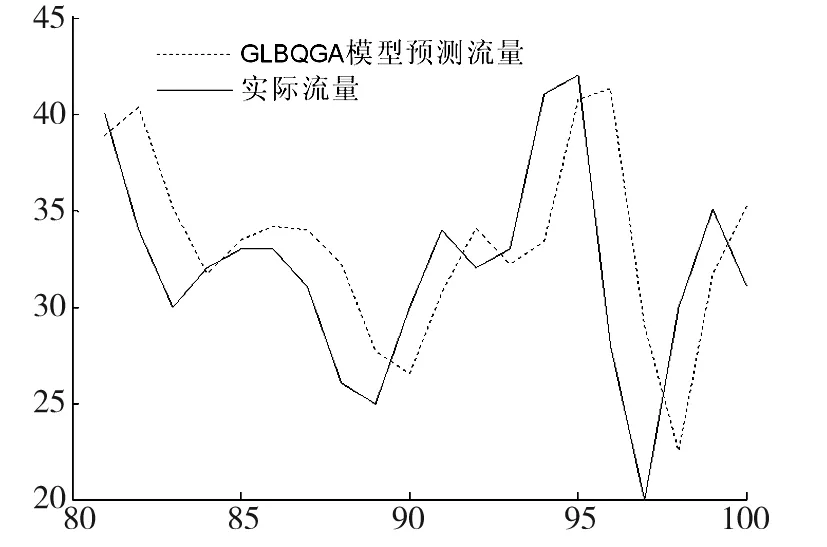
图6 GLBQGA模型超前三步预测曲线Fig.6 Three-step ahead forecasting results of GLBQGA

AR(8)模型和基于GLBQGA算法优化的AR(8)模型超前三步预测结果的MAPE指标如表2所示：

表2 AR(8)模型和GLBQGA算法优化的AR(8)模型超前三步预测结果对比

Table 2 Comparison of Three-step ahead forecasting results of AR(8) and GLBQGA

预测模型后20个样本超前三步预测结果的MAPE指标AR(8)26.75%GLBQGA算法优化的AR(8)模型13.21%

从图5、图6和表2可知，GLBQGA算法优化的AR(8)模型的预测效果优于传统的AR(8)模型，以超前三步预测为例，预测平均相对误差由26.75%下降到13.21%，下降了50.62%。应用结果表明，相比传统的AR模型，基于本文提出的GLBQGA算法所构建的短时交通流多步预测模型在超前多步预测时有着更高的精度，对实际交通流特性的刻画也更为理想。

5 结论

1)提出基于全局-局部变异的Bloch球面量子遗传算法GLBQGA，该算法在传统Bloch球面量子遗传算法基础上，通过引入全局-局部变异算子改进传统BQGA算法的变异操作，使GLBQGA算法在搜索后期具备较强的局部搜索能力，有效避免了算法振荡，提高了算法精度；通过合理限制量子转角参数范围在保证传统BQGA算法搜索空间不变的前提下提高算法效率。

2)基于GLBQGA算法的机车二系支承载荷优化调整实验结果证明，在不增加时间复杂度的前提下，GLBQGA算法较标准遗传算法有着更为强大的搜索全局最优精确解的能力。

3) 针对短时交通流多步预测问题的特点，提出一种基于GLBQGA算法优化AR模型的短时交通流多步预测方法，实验结果表明其预测效果明显优于传统AR模型，为交通流多步预测提供了一种新思路。

[1] Nowotniak R, Kucharski J. Higher-order quantum-inspired genetic algorithms[C]// Computer Science and Information Systems (FedCSIS), 2014 Federated Conference on. IEEE, 2014:465-470.

[2] Malossini A, Blanzieri E, Calarco T. Quantum genetic optimization[J]. Evolutionary Computation, IEEE Transactions on, 2008, 12(2): 231-241.

[3] Khorsand A R, Akbarzadeh-T M R. Quantum gate optimization in a meta-level genetic quantum algorithm[C]//Systems, Man and Cybernetics, 2005 IEEE International Conference on. IEEE, 2005, 4: 3055-3062.

[4] 熊焰,陈欢欢,苗付友,等.一种解决组合优化问题的量子遗传算法QGA[J]. 电子学报,2004,32(11):1855-1858. XIONG Yan, CHEN Huanhuan, MIAO Fuyou, et al. A quantum genetic algorithm to solve combinatorial optimization problem[J]. ACTA Electronica Sinica, 2004,32(11):1855-1858.

[5] 沈微微, 华明正, 李敏. 量子遗传进化算法的收敛性研究[J]. 信息技术, 2013(10):161-164. SHEN Weiwei, HUA Mingzheng, LI Min. Study on convergence of quantum genetic evolution algorithm[J]. Information Technology, 2013(10):161-164.

[6] 易正俊，侯坤，何荣花. 自适应Bloch球面的量子遗传算法[J]. 计算机工程与应用, 2012,48(35):57-61. YI Zhenjun，HOU Kun，HE Ronghua．Adaptive quantum genetic algorithm based on bloch sphere[J]．Computer Engineering and Applications, 2012, 48(35):57-61.

[7] 张葛祥, 金炜东. 量子遗传算法的改进及其应用[J]. 西南交通大学学报, 2003, 38(6):717-722. ZHANG Gexiang, JIN Weidong. Improvement of quantum genetic algorithm and its application[J]. Journal of Southwest Jiaotong University, 2003, 38(6):717-722.

[8] 李盼池. 基于量子位Bloch坐标的量子遗传算法及其应用[J]. 控制理论与应用, 2008, 25(6):985-989. LI Pan-chi. Quantum genetic algorithm based on Bloch coordinates of qubits and its application[J]. Control Theory & Applications, 2008, 25(6):985-989.

[9] 李士勇, 李盼池. 量子计算与量子优化算法[M]. 哈尔滨：哈尔滨工业大学出版社, 2009,5: 86-95. Li Shiyong, Li Panchi. Quantum computation and quantum optimization algorithms[M]. HARBIN Institute of Technology Press, 2009,5: 86-95.

[10] 赵义武, 牛庆银, 王宪成. 遗传算法与蚁群算法的融合研究[J]. 科学技术与工程, 2010,10(16):4017-4020. ZHAO Yiwu,NIU Qingyin,WANG Xiancheng.Study on the combination of genetin algorith and Ant Algoicthm[J].Scicence Fechnology and Engineering, 2010,10(16):4017-4020.

[11] Pan D, Wang M, Zhu Y, et al. An optimization algorithm for locomotive secondary spring load adjustment based on artificial immune[J]. Journal of Central South University, 2013, 20(12): 3497-3503.

[12] 潘迪夫, 黎航, 韩锟. 基于遗传算法的机车二系支承载荷调整优化方法[J]. 中国铁道科学, 2005, 26(3): 83-87. PAN Difu , LI Hang , HAN Kun. Optimization model of locomotive secondary spring load adjustment based on genetic algorithm[J]. China Railway Science, 2005, 26(3): 83-87.

[13] 韩锟, 潘迪夫. 基于混合算法的机车二系弹簧载荷调整优化方法[J]. 中国铁道科学, 2006, 27(2): 88-92. HAN Kun , PAN Difu. Optimization model for adjustment of locomotive secondary spring load based on hybrid algorithm[J]. CHINA RAILWAY SCIENCE, 2006, 27(2): 88-92.

[14] 杨本磊, 潘迪夫. 基于人工鱼群算法的机车二系支承载荷调整优化方法[J]. 计算机与现代化, 2011,(1): 53-54. YANG Benlei, PAN Difu. Optimization model of locomotive secondary spring load adjustment based on artificial fish-swarm algorithm[J].Computer and Modevnization, 2011,(1): 53-54.

[15] 潘迪夫, 韩锟, 曾亚波,等. 车体称重调簧试验装置及其应用[J]. 电力机车与城轨车辆, 2003, 26(5):37-39. PAN Difu, HAN Kun, ZENG Yabo, et al. Locomotive secondary spring load test device and its application[J]. Electric Locomotives & Transit Vehicles, 2003, 26(5):37-39.

[16] 王秋兰. 短时交通参数多步预测方法研究[D]. 长春: 吉林大学, 2012. WANG Qiulan. Study on the multi-steps prediction method of short-time traffic parameters[D]. Changchun: Jilin University, 2012.

[17] 宋驰, 沈国江. 短时交通流预测模型综述[J]. 自动化博览, 2012(6):84-87. SONG Chi, SHEN Guojiang. Survey on short-term traffic flow forecasting modelling[J]. Automation Panorama,2012(6):84-87.

[18] 韩超, 宋苏, 王成红. 一种改进的短时交通流多步自适应预测算法[J]. 公路交通科技, 2005, 22 (1):115-118. HAN Chao , SONG Su , WANG Chenghong. An improved multi-step adaptive forecasting method for short-term traffic flow[J]. Journal of Highway and Transportation Research and Development, 2005, 22 (1):115-118.

[19] 李明涛. 快速路短时间尺度地点交通参数多步预测方法研究[D]. 长春:吉林大学，2009. LI Mingtao. Study on the methods of located traffic parameters short-term and multi-steps prediction for expressway[D]. Changchun:: Jilin University, 2009.

[20] Soleimanimehr H, Nategh M J, Amini S. Prediction of machining force and surface roughness in ultrasonic vibration-assisted turning using neural networks[J]. Advanced Materials Research, 2009, 83(12): 326～334.

An improved bloch spherical quantum genetic algorithm and its application

LI Jiacai, HAN Kun, BAO Tianzhe

(School of Traffic &Transportation Engineering, Central South University, Changsha 410075, China)

An improved Bloch Spherical Quantum Genetic Algorithm (GLBQGA) was proposed to overcome the shortcoming of the quantum genetic algorithm (QGA), i.e., local optimization, when it is used for the optimization of continuous functions with many extreme values. In order to make sure the algorithm can converge to the exact solution of optimal local neighborhood search after searching global optimum approximation, a new variation of global-local operator was introduced, and a local search mechanism was established based on globally attributes. The quantum angular value program was further optimized, while ensuring the search space and improving the efficiency of search. Calculative examples were made in optimization of locomotive secondary uniform load distribution and application of short-time traffic flow prediction, and the results show that GLBQGA can overcome the QGA premature convergence problems, and improve precision without increasing search time significantly.

bloch spherical coordinate; quantum genetic algorithm; spring adjustment; traffic flow prediction

2016-03-05

国家自然科学基金资助项目(51305467)

韩锟(1977-)，女，湖北随州人，副教授，博士，从事载运工具智能测控技术及性能优化研究；E-mail：hkun@csu.edu.cn

TP301.6；U260.72

A

1672-7029(2016)11-2262-08