河水位变化影响下水下隧道的施工力学行为

岳健 ,谭仁华 , 安永林 , 刘运思

(1.湖南科技大学 土木工程学院, 湖南 湘潭 411201；2.湖南科技大学 岩土工程稳定控制与健康监测省重点实验室，湖南 湘潭 411201)



河水位变化影响下水下隧道的施工力学行为

岳健1，2,谭仁华1，2, 安永林1，2, 刘运思1，2

(1.湖南科技大学 土木工程学院, 湖南 湘潭 411201；2.湖南科技大学 岩土工程稳定控制与健康监测省重点实验室，湖南 湘潭 411201)

针对矿山法施工的下穿河流水下小净距交通隧道，结合数值模拟与现场监测，研究在河水位变化影响下的隧道施工力学行为。首先，考虑河水位变化、隧道开挖面位置变化对围岩的应力场与渗流场的影响，建立三维计算模型，根据现场监测得到的河水位-施工步变化曲线，在模型中设置了92种河水位与施工步的对应状态；然后分析计算结果，并对比数值模拟结果与现场监测结果；最后计算分析河水位暴涨与骤降的8种工况。研究结果表明：在相邻洞施工的影响下，本洞上台阶初衬的最大压应力出现在拱脚；相比前一施工步，施工仅仅向前推进1步的同时如果河水位暴涨5 m，会明显恶化本洞紧邻施工段的初衬的受力状况。基于研究结果提出了若干工程建议。

水下小净距隧道；河水位变化；施工力学行为；矿山法

对于跨越江、河、湖、海的水下交通隧道，研究上覆水体的水位变化对隧道力学行为的影响具有重要的工程意义[1-4]。许金华[5]比较了不同江水位下盾构隧道管片承受水压力的分布情况；张志强[6]研究指出不同水位条件下矿山法海底隧道要采取不同的排水量控制标准；李鹏飞[7]研究表明海水深度对矿山法海底隧道风化槽段的围岩稳定性影响显著；于洪丹[8]指出海洋潮汐荷载循环变化，非常不利于矿山法海底隧道衬砌的长期稳定；林存刚[9]研究发现在潮汐引起钱塘江水位变化的影响下，某运营盾构隧道的钢筋应变和围压随水位变化发生等周期的同步波动。不同学者针对不同工况开展研究，取得了重要的研究成果。值得注意的是：1)感潮性河流与非感潮性河流的水位变化情况不同，前者的河水位变化循环快，甚至半日或一日就循环一次，而后者的河水位变化循环要慢的多，两种不同的河水位变化情况对下方隧道受力性状产生的影响也不同；2)隧道采用不同的修建方法(矿山法、盾构法、沉管法等)，隧道的施工工序变化、渗流边界变化等存在较大不同，因此水位变化影响下的隧道受力性状也不同。

对于采用矿山法施工的下穿河流的水下小净距交通隧道，本文提到的“隧道开挖面位置”指的是隧道正前方临空的竖直岩面的位置，隧道开挖面位置随着各施工工序的循环作业而沿纵向逐步向前推进，即隧道开挖面的位置随着施工步而变；在隧道开挖面位置变化的同时，上方的河水位可能也在变化，即河水位变化与隧道开挖面位置变化有可能同时发生，而且在整个施工期间两个变化量之间存在复杂的对应关系，会引起隧道围岩的应力场与渗流场发生复杂变化，目前对于上述情况下的隧道施工力学行为的研究还鲜见报道。本文以矿山法施工的下穿浏阳河(非感潮性河流)的水下小净距公路隧道为工程背景，结合数值模拟与现场监测，研究在河水位变化影响下隧道施工过程的力学行为。

1 基于现场监测建立数值计算模型

长沙市浏阳河公路隧道设置水平平行双洞，单洞开挖宽度11.9 m，开挖高度10.4 m。选取位于浏阳河下方50 m长的一段隧道作为研究对象，研究区段内相邻两洞的净距为1.5B(B为单洞开挖宽度)，水下岩土覆盖层厚度仅为16 m。建立研究区段的三维计算模型如图1与图2所示，整个模型宽300 m，高150 m，纵向长50 m。模型中的地层自上而下分别为：厚1 m的人工填土，厚3.5 m的粉质黏土，厚3.5 m的卵石层，余下为强风化砾岩层。隧道从强风化砾岩中穿过。根据地质勘查报告与相关规范，选定计算参数如表1所示。依次采用全断面预注浆、管棚、小导管对围岩进行超前加固，在施工过程模拟中，采用将围岩属性修改为超前加固区属性的方法来模拟超前加固的作用。隧道全环喷射厚25 cm的 C25混凝土，将喷砼和型钢拱架视作一个整体，统称为“初衬”。初衬为线弹性模型，其余材料均为摩尔-库仑模型。模型顶面为河水与岩土的交界面，模型顶边界的位移自由，其余界面均约束法向位移。

图1 模型整体Fig.1 Model entirety

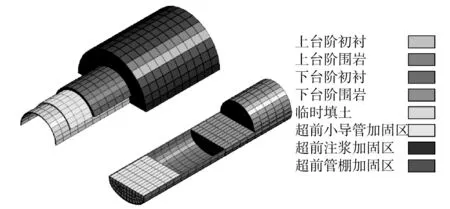
图2 洞室周边的网格划分Fig.2 Mesh generation around the tunnel

隧道采用上下台阶法开挖，共有先行洞上台阶、后行洞上台阶、先行洞下台阶、后行洞下台阶4个开挖面。图3为施工步变化示意图，图3中的数字表示施工步序号，方框中每一施工步的进尺均为2.5 m。方框中未加括号的序号表示施工上台阶，上台阶的每个大施工步包括施作超前小导管支护以及开挖与施作初衬、渗流、耦合等细步；方框中加括号的序号表示施工下台阶，下台阶的每个大施工步包括开挖与施作初衬、回填土至上下台阶开挖分界线(以方便施工车辆通行及抑制底部上浮)、渗流、耦合等细步。先行洞上台阶开挖面与后行洞上台阶开挖面的纵向间距为25 m，同一个洞的上台阶开挖面与下台阶开挖面的纵向间距为50 m。整个施工工程共分为92个大的施工步。

在施工现场用全站仪实时量测隧道各开挖面到达的里程，隧道附近桥墩上设置有水尺，结合水尺观测与全站仪观测得到施工步对应的河水位。根据现场监测结果，得到了如图4所示的河水位变化与施工步变化的对应曲线(3月～6月)，分析发现：浏阳河水位变化较为复杂，这是由于不仅降雨变化会引起河水位变化，河道附近的生活、生产、灌溉、防旱防涝、工程建设等不定期的抽排水作业也会引起河水位变化，各种复杂因素共同作用使河水位反复升降。为了便于研究河水位的变化，图4将河水位的起算点设于计算模型的顶面，即河水位与水深的数值一样。

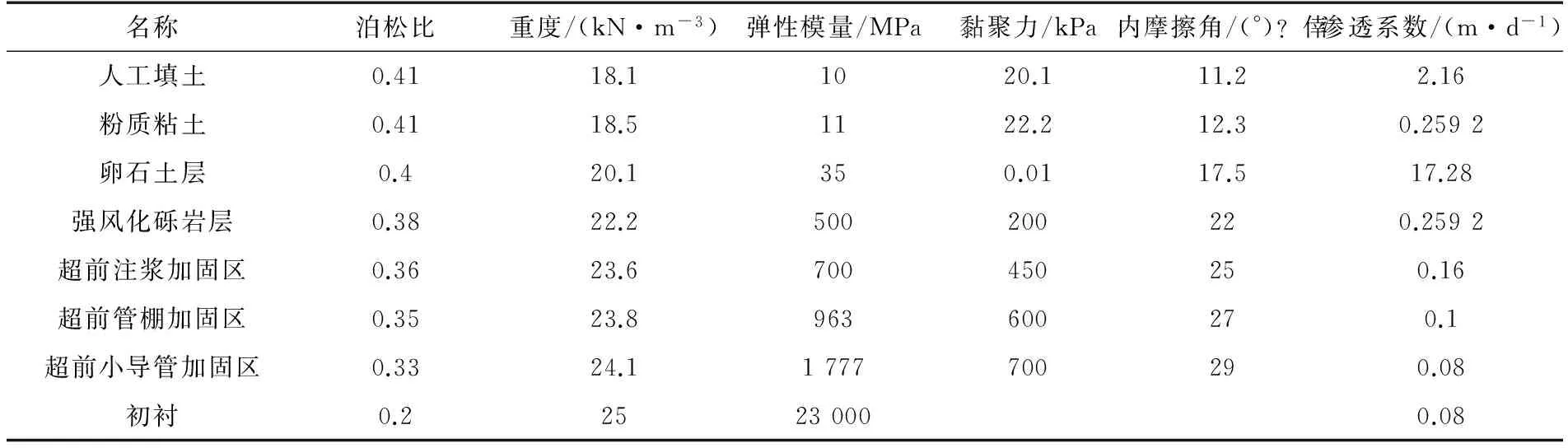
表1 材料的计算参数

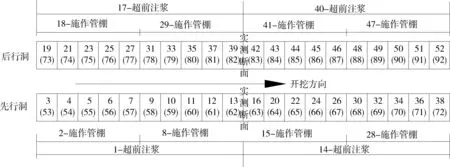
图3 施工步变化示意图Fig.3 Sketch of change of construction step

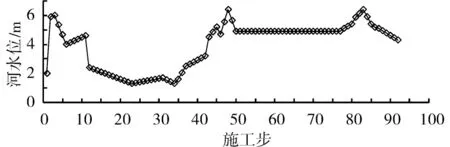
图4 河水位-施工步曲线Fig.4 River water level-construction step curve

笔者在浏阳河隧道施工现场实时观察隧道内的渗水情况，发现隧道临空面的水并不是急速喷出，而是慢慢渗出的；在研究区段的中部布置了两个洞内的现场应力监测断面(如图3所示)，监测部位如图5所示，通过现场监测得到了如图6所示的初衬背后水压力随施工步的变化情况，结合图3与图4分析可知，在河水位与开挖面位置同时变化的影响下，在施作二衬以前的上台阶初衬背后的水压力都比较小，均不超过 16 kPa；又考虑到水从初衬背后渗流过初衬后，水压力有可能会进一步折减，因此将随着施工推进出现的上台阶围岩临空面、上台阶初衬临空面、下台阶填土临空面的压力水头均设为0(施作完下台阶初衬后会立即进行临时填土)，后文会对比数值模拟结果与现场监测结果进行进一步验证。现场调查表明所研究施工阶段内的河底冲淤现象不明显，因此设置河底标高不变，河水深度的变化量与河水位的变化量等值，可以由现场实测得到，因此将模型顶面的总水头设为“模型高度+河水深度”，本文主要考虑河水向隧道内渗流，而且隧道施工对渗流场的扰动范围有限，模型计算区域又比较大，因此设定模型的其余边界面均不与外界进行水量交换。

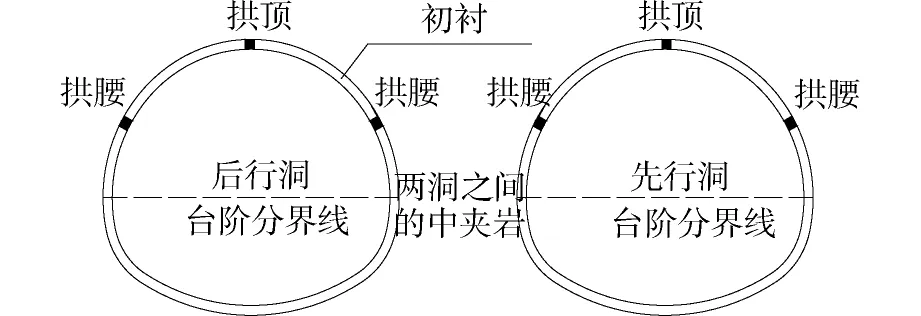
图5 监测的关键部位示意图Fig.5 Diagrammatic drawing of key position of measurement

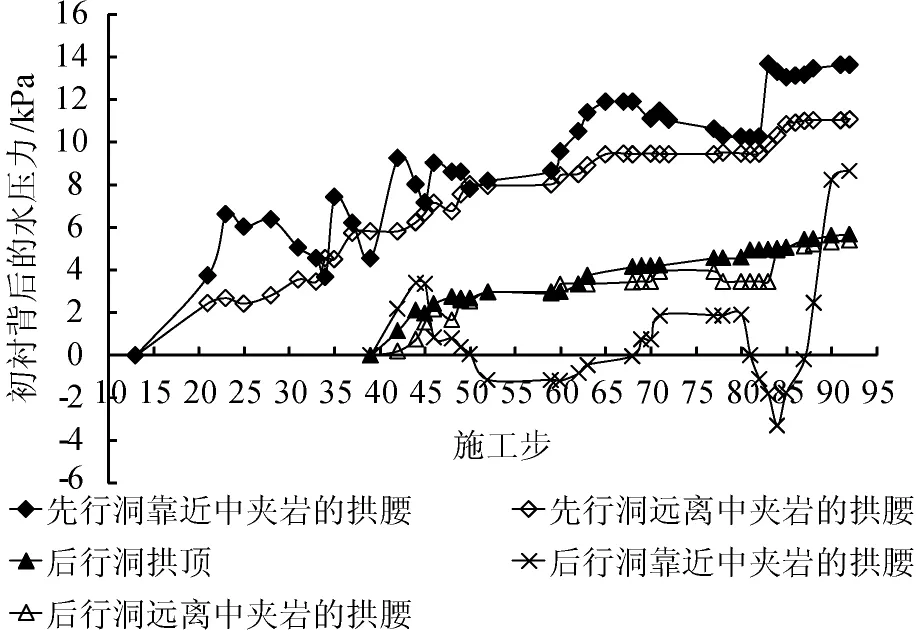
图6 水压力的现场监测结果Fig.6 Field monitoring result of water pressure

目前考虑渗流场与应力场双重变化影响的数值计算理论有多种，在用于分析隧道复杂的施工力学行为上均存在优点与缺点，可根据现场具体的工程情况与研究的目的进行选择[10-15]。本文在设置模型的计算步骤时，要考虑河水位变化、隧道开挖面位置变化对围岩的应力场与渗流场的影响，共设置了92种河水位与施工步的对应状态，相当于把图4所示的河水位变化曲线嵌入到变化的施工过程中进行计算，因此模型整个施工过程的渗流边界、荷载、单元属性等均会频繁变化，计算步骤多，计算工作量大，采用何种计算原理还要考虑计算结果的收敛性以及工程应用的方便。河水源源不断向隧道内渗流与无水补给隧道的排水渗流并不相同，根据浏阳河隧道的具体情况，本文假设河下的岩土始终饱和，采用的计算原理说明如下：在时间Δt内，完成了如图3方框内所示的某一施工步，使开挖面的位置发生变化，这一方面导致围岩的应力场发生变化(如开挖导致围岩应力释放)；另一方面改变了渗流边界(如开挖形成新的压力水头为“0”的临空面)，隧道周围介质的渗透系数也发生了变化(如部分围岩被初衬代替)，从而改变了渗流场。在完成上述某一施工步的同时，河水位升高或降低了Δh，这一方面导致作用在模型顶面(河水与岩土的交界面)的河水压力变化了Δp，从而改变了围岩的应力场；另一方面导致模型顶面的总水头变化了ΔH，从而改变了渗流场。由上所述，河水位与隧道开挖面位置同时变化会直接改变应力场，首先通过本构模型求出直接变化后的应力场；然后，考虑到河水位与隧道开挖面位置同时变化又会改变渗流场，根据渗流方程(1)进行求解，得到变化后的总水头：

(1)式中：H为总水头； kx，ky和kz分别为x，y和z方向的渗透系数，这里假定kx=ky=kz；Q为流量； Θ为体积含水率；t为时间。从总水头中减去位置水头得到压力水头，再将压力水头与水的重度相乘得到孔隙水压力。然后根据式(2)的有效应力原理，将孔隙水压力代入先前已经求出来的应力场中，再通过材料的本构模型求出渗流场与应力场双场变化后的耦合结果，从而得到河水位与隧道开挖面位置同时变化后的隧道与围岩的应力与位移。

(2)

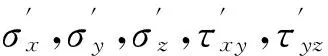
2 计算结果分析及与监测结果对比

限于篇幅，下文的分析说明内容只给出若干代表性的图表。

2.1 河床特征点的竖向位移

在现场监测横剖面正上方的河床(河水与岩土的交界线)取7个特征点，其中A点对应先行洞的拱顶，B点对应后行洞的拱顶，C点在中夹岩的纵向对称面上，远离中夹岩的D点距离A点为15 m，远离中夹岩的E点距离B点为15 m，远离中夹岩的F点距离A点为42 m，远离中夹岩的G点距离B点为42 m。图7为数值模拟得到的河床特征点的竖向位移随施工步的变化曲线，结合图3与图4分析计算结果可知：随着施工推进，在河水位与隧道开挖面位置同时变化的影响下，在多数施工步内河床都下沉，但在少数施工步内由于河水位降低产生的影响大于开挖卸载等因素产生的影响，会导致河床上升。在隧道开挖期间，河床各特征点的累计沉降均不超过20 mm，但应注意河床各点反复不均匀升降易导致河床产生裂缝，在水压下裂缝有可能扩展直达隧道而造成突水，因此隧道施工要尽量减小对河水下浅层河床的扰动，例如隧道之上的超前注浆加固范围不能太大，注浆压力也不能太大，这样有些地方的超前注浆加固效果会较差，应采用管棚注浆联合小导管注浆予以弥补。

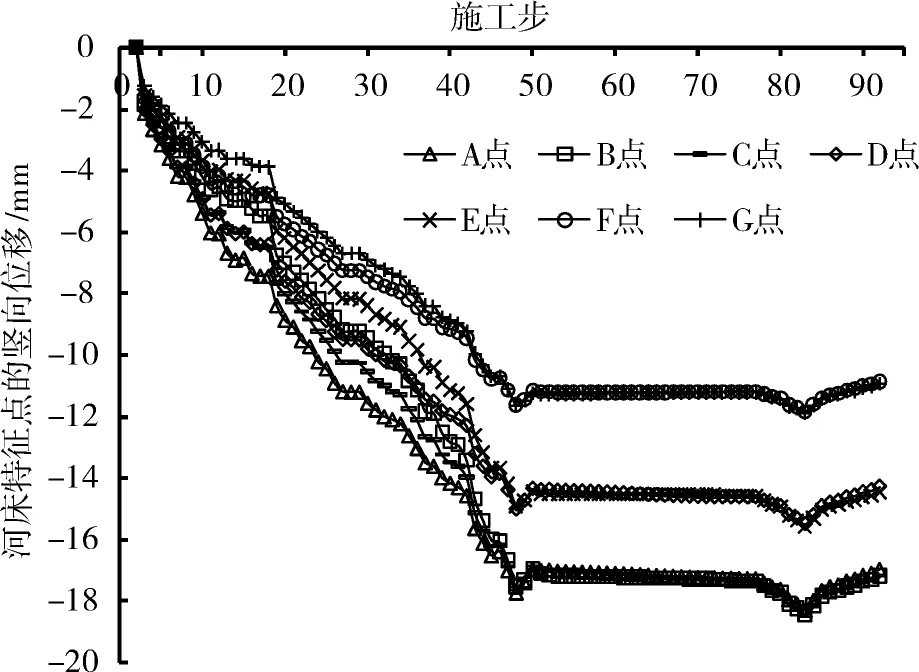
图7 河床点竖向位移的变化曲线Fig.7 Change curves of vertical displacement of riverbed points

2.2 水的渗流速度

图8给出了施工步26对应的水渗流速度的数值模拟云图。分析计算结果得出：在同一横剖面，在后行洞上台阶开挖以前，超前开挖先行洞上台阶会增大后行洞未开挖区域的水渗流速度，从而增强水对后行洞围岩的渗透破坏能力，会预先恶化后行洞的围岩条件，应适当加强后行洞的超前支护；对于隧道纵向平顺且初衬与围岩紧密接触的情况，水沿隧道横剖面的渗流速度大于沿隧道纵向的渗流速度，上覆河水主要沿隧道横剖面向洞内渗流。

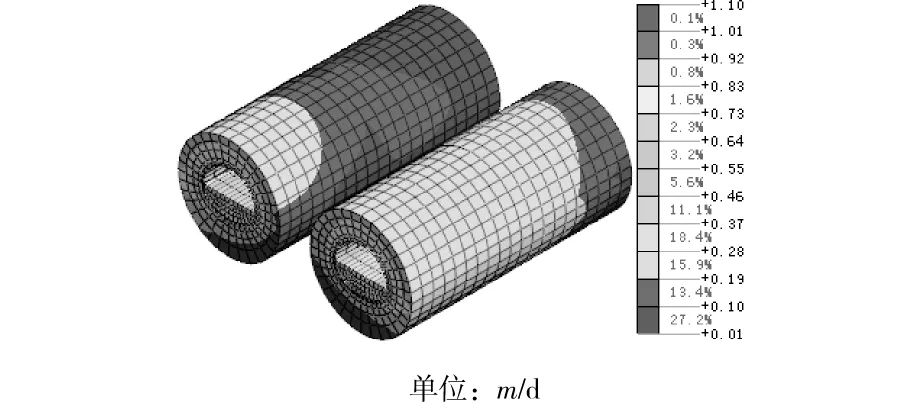
图8 水在隧道横剖面内的合渗流速度Fig.8 Total flow velocity at transverse section

2.3 初衬背后的水压力

图9与图10给出了数值模拟最后一步即施工步92的水压力分布(初衬封闭环内有临时填土),结合现场监测图6进行分析，可以看出同一部位的初衬背后水压力的数值模拟值与现场监测值最大相差仅为6 kPa，表明二者相差不大；初衬背后各处的水压力均明显小于相应的静水压力，发生了明显的折减现象，这是由于隧道与河流之间存在的岩土层可以消耗河水下渗的能量，在河水位与隧道开挖面位置同时变化的影响下，洞室附近区域的渗流场不断变化，初衬背后的水压力是一种动水压力，各种临空面的存在均可以透水泄压；建议类似隧道在设计初衬时，如果在初衬背后不进行专门的注浆填充，并且初衬不采用抗渗混凝土，即初衬可以透水泄压，这种情况下初衬背后的水压力不宜按静水压力计算，应进行相应的折减；相比之下，上台阶初衬背后的水压力较小，下台阶初衬背后的水压力较大，仰拱底处的水压力最大，为94 kPa，主要原因在于渗水优先向底部汇集，而底部初衬离填土临空面较远，透水泄压的能力较弱。

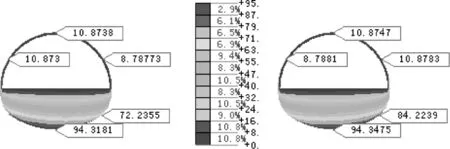
单位：kPa图9 初衬背后的水压力分布Fig.9 Layout of water pressure behind initial lining

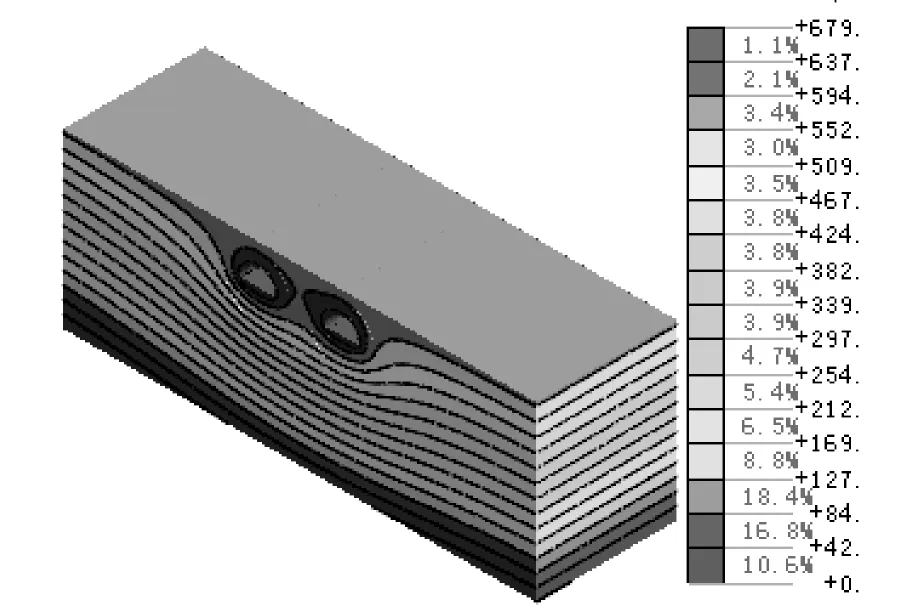
单位：kPa图10 洞室附近区域的孔隙水压力分布Fig.10 Layout of pore water pressure near caves

2.4 初衬的应力

以监测断面为起点沿隧道纵向取2.5 m长的一段隧道为这里的分析对象。图11(a)与图11(c)为施工后行洞上台阶后的先行洞上台阶初衬的主应力分布，图11(b)与图11(d)为施工先行洞下台阶后的后行洞上台阶初衬的主应力分布，计算表明：在相邻洞施工的影响下，本洞上台阶初衬的最大压应力均出现在拱脚，建议增设上台阶初衬的锁脚锚杆；上台阶初衬的主拉应力主要分布在初衬的内侧，其中的最大拉应力发生在拱顶内侧，建议型钢拱架不要在拱顶设置接头。

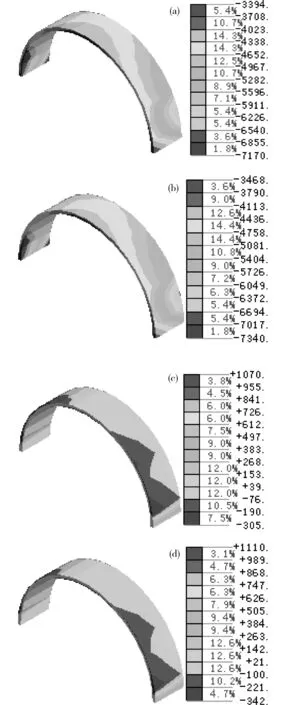
单位：kPa(a)施工步42的最小主应力;(b)施工步63的最小主应力;(c)施工步42的最大主应力;(d)施工步63的最大主应力图11 初衬的主应力分布Fig.11 Layout of principal stress of initial lining

图12为上台阶初衬的绝对值最大的压应力随施工步的变化曲线，结合图3与图4分析得出：

1)后行洞上台阶施作超前小导管、开挖及初衬并且河水位升高1.3 m，使先行洞上台阶初衬的最大压应力增大了98 kPa；先行洞下台阶开挖、初衬及临时填土并且河水位不变，使后行洞上台阶初衬的最大压应力增加6 kPa；后行洞下台阶开挖、初衬及临时填土并且河水位升高0.3 m，使先行洞上台阶初衬的最大压应力增大了57 kPa。

2)先行洞下台阶开挖、初衬及临时填土并且河水位不变，使正上方的上台阶初衬的最大压应力减小了1 677 kPa；后行洞下台阶开挖、初衬及临时填土并且河水位升高0.3 m，使正上方的上台阶初衬的最大压应力减小了1 632 kPa。这是由于施作下台阶初衬使初衬闭合成环后，上台阶初衬的应力可以向下台阶初衬传递，上台阶初衬的应力集中程度被明显消弱了；透水性相对较差的下台阶初衬代替了原来透水性好的围岩，使底部受到的水浮力增大，抵消了一部分上台阶初衬受到的围岩压力。

图12 初衬最大压应力的变化曲线Fig.12 Change curves of maximum crushing stress of initial lining

2.5 初衬的拱顶沉降

图13对比了监测断面初衬拱顶沉降的现场监测结果与数值模拟结果，结合图3与图4分析可知：初衬拱顶沉降的计算曲线与监测曲线有的部分吻合较好，有的部分则存在一些差距，存在差距的主要原因是：数值模拟假设岩土为连续介质，假设渗透系数等力学参数具有各向同性，这均与实际情况存在一些差距；数值模拟为了得到普遍性规律将渗水点布置得较为均匀，而现场的渗水点位置具有一定的随机性。总体上数值模拟结果与现场监测结果相差不大，二者均表明：随着施工推进，初衬拱顶以下沉为主，但在某些施工步会出现上升现象，这是由于隧道开挖、河水位上升等因素会使拱顶下沉，河水位下降等因素则会使拱顶上升，而且各因素的影响作用强弱均会随着施工推进而发生变化，多种因素综合作用决定某一施工步的拱顶升降；在河水位变化的影响下，即便经历较长时间，初衬的拱顶沉降也可能不会趋于稳定。

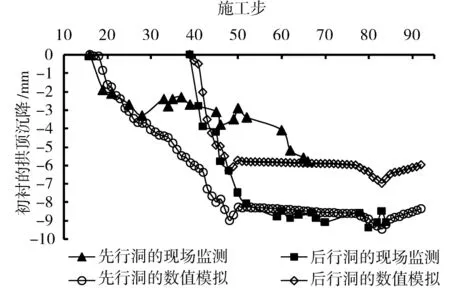
图13 初衬拱顶沉降的变化曲线Fig.13 Change curves of crown settlement of initial lining

隧道施工期间未发生涌水灾害，计算表明，沿隧道纵向每1 m长的渗水量均不超过20 m3/d。上述初衬背后的水压力、初衬拱顶沉降的数值模拟结果与现场监测结果均相差不大，差距在工程应用可接受的范围内，表明本文的数值模拟结果具有参考价值，可在一定程度上弥补现场监测的不足。

3 河水位暴涨与骤降的情况

前文研究的是浏阳河隧道某一特定区段在特定时间段内的实际河水位变化情况，现场监测表明上述条件下的一天之内的河水位变化量均不超过1.5 m，一般不会超过1 m。由于导致河水位变化的因素复杂多变而且有时不可预见，类似水下隧道在短时间内，在施工某一步的同时河水位的变化量可能会非常大(比如浏阳河水位曾在一天之内暴涨了5 m)，有必要对这类情况进行研究。根据图3选取4个典型施工步分别为：施工步12(施工先行洞上台阶)、施工步43(施工后行洞上台阶)、施工步61(施工先行洞下台阶)、施工步84(施工后行洞下台阶)。假设在进行某一典型施工步之前的河水位不变(为2 m或7 m)，接下来一天之内河水位由2 m暴涨5 m至7 m或由7 m骤降5 m至2 m，与此同时完成这一典型施工步，然后假设河水位不再变化，计算至隧道全开挖完，共计算了8种工况。限于篇幅，只给出表2与表3，反映了河水位暴涨或骤降的同时施工仅仅推进一步对邻近初衬的叠加影响，其中的“初衬拱顶竖向位移”与“初衬最大压应力”均针对的是紧邻典型施工段的已经施作好的一段纵向长2.5 m的初衬(相邻洞取对应区段进行分析)，并不是典型施工步内施作的初衬；“步数”一列为完成某一典型施工步后的量值，“变化”一列为典型施工步量值减去前一施工步量值所得的值占前一施工步量值的百分比。分析计算结果得到：河水位暴涨或骤降使各段初衬的竖向位移与最大压应力在短时间内均发生了明显变化。相比前一施工步，施工仅仅向前推进1步的同时如果河水位暴涨5 m，就使本洞紧邻施工段的初衬的拱顶沉降至少增大30%、初衬的最大压应力至少增加20%，明显恶化了本洞紧邻施工段的初衬的受力状况，也恶化了相邻洞初衬的受力状况。如果河水位暴涨至高位后还要持续较长时间，而施工要连续不断向前推进，在这种情况下为了防止累积效应使初衬处于危险的受力状态，建议将开挖方法由上下台阶法改为CRD法，缩短每循环开挖进尺，加密型钢拱架布置，增设防排水设施，加强现场监测，必要时暂停向前开挖。

表2 河水位暴涨的计算结果

表3 河水位骤降的计算结果

4 结论

1)考虑河水位变化、隧道开挖面位置变化对围岩的应力场与渗流场的影响，建立三维计算模型；基于现场监测结果，在模型中设置渗流边界条件、河水位与施工步的对应状态；通过对比数值模拟结果与现场监测结果，表明数值模拟结果具有参考价值，可在一定程度上弥补现场监测的不足。

2)隧道施工应尽量减小对河水下浅层河床的扰动；在同一横剖面，超前开挖先行洞上台阶会增大后行洞未开挖区域的水渗流速度，会预先恶化后行洞的围岩条件；初衬背后各处的水压力均明显小于相应的静水压力；在相邻洞施工的影响下，本洞上台阶初衬的最大压应力出现在拱脚。

3)相比前一施工步，施工仅仅向前推进1步的同时如果河水位暴涨5 m，会明显恶化本洞紧邻施工段的初衬的受力状况，也恶化了相邻洞初衬的受力状况，提出了相应的工程建议。

致谢：感谢中铁隧道集团与中铁第四勘察设计院集团有限公司对本文现场监测工作给予的帮助。

[1] DAVID M. Analysis of consolidation with constant rate of displacement[J]. Canadian Geotechnical Journal, 2016, 53(5): 740-752.

[2] JUN S, SUNG K, MYNUG S. Attenuation of blast vibration in tunneling using a pre-cut discontinuity[J]. Tunnelling and Underground Space Technology, 2016, 52(1): 30-37.

[3] 傅鹤林, 陈琛, 张加兵. 衬砌脱空对现役隧道结构安全性影响研究[J]. 铁道科学与工程学报, 2016, 13(3): 517-522. FU Helin, CHEN Chen, ZHANG Jiabing. Research about cavity lining impact on structural safety for tunnel in service[J]. Journal of Railway Science and Engineering, 2016, 13(3): 517-522.

[4] 雷波, 漆泰岳, 王睿. 海底隧道不同防排水条件下衬砌结构开裂情况研究[J]. 铁道科学与工程学报, 2015, 12(4): 859-865. LEI Bo, QI Taiyue, WANG Rui. Study on the lining crack of subsea tunnel in the different conditions of waterproof and drainage[J]. Journal of Railway Science and Engineering, 2015, 12(4): 859-865.

[5] 许金华, 何川, 夏炜洋.水下盾构隧道渗流场应力场耦合效应研究[J].岩土力学, 2009, 30(11): 3519-3527. XU Jinhua, HE Chuan, XIA Weiyang. Research on coupling seepage field and stress field analyses of underwater shield tunnel[J]. Rock and Soil Mechanics, 2009, 30(11): 3519-3527.

[6] 张志强, 何本国, 何川.水底隧道饱水地层衬砌作用荷载研究[J].岩土力学, 2010, 31(8): 2465-2470. ZHANG Zhiqiang, HE Benguo, HE Chuan. Study of load of lining under condition of saturated stratum for underwater tunnels [J]. Rock and Soil Mechanics, 2010, 31(8): 2465-2470.

[7] 李鹏飞, 张顶立, 李兵.海底隧道施工过程中围岩稳定性的流固耦合分析[J].中国铁道科学, 2010, 31(3): 35-41. LI Pengfei, ZHANG Dingli, LI Bing. Coupled fluid-solid analysis of the surrounding rock stability of the subsea tunnel during construction process [J]. China Railway Science, 2010, 31(3):35-41.

[8] 于洪丹, 陈卫忠, 郭小红.潮汐对跨海峡隧道衬砌稳定性影响研究[J].岩石力学与工程学报, 2009, 28(增1): 2905-2914. YU Hongdan, CHEN Weizhong, GUO Xiaohong. Research on effect of tide on stabilities of channel tunnel lining[J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(S1): 2905-2914.

[9] 林存刚. 盾构掘进地面隆陷及潮汐作用江底盾构隧道性状研究[D].杭州: 浙江大学, 2014: 174-213. LIN Cungang.Research on shield tunnelling-induced ground surface heave and subsidence and behavior of underwater shield-driven tunnels subject to tidal bores[D]. Hangzhou: Zhejiang University, 2014.

[10] User's manual of Midas-gts[Z]. Beijing: Midas Technology Co.,Ltd of Beijing, 2014: 40-68.

[11] LI Z, KENICHI S, PETER W. Long-term performance of cast-iron tunnel cross passage in London clay[J]. Tunnelling and Underground Space Technology, 2015, 50(4):152-170.

[12] LI B, HONG Y, GAO B. Numerical parametric study on stability and deformation of tunnel face reinforced with face bolts[J]. Tunnelling and Underground Space Technology, 2015, 47(1): 73-80.

[13] 陈卫忠, 伍国军, 贾善坡. ABAQUS在隧道及地下工程中的应用[M]. 北京: 中国水利水电出版社, 2010: 228-238. CHENG Weizhong, WU Guojun, JIA Shanpo. Application in tunnel and underground construction of ABAQUS[M]. Beijing: China WaterPower Press, 2010: 228-238.

[14] 刘波, 韩彦辉. FLAC 原理、实例与应用指南[M]. 北京:人民交通出版社, 2005: 46-55. LIU Bo, HAN Yanhui. Principle, example and application guide of FLAC[M]. Beijing: China Communications Press, 2005: 46-55.

[15] 何川, 谢红强. 多场耦合分析在隧道工程中的应用[M]. 成都: 西南交通大学出版社, 2007: 3-13. HE Chuan, XIE Hongqiang. Application in tunnel engineering of multi-field coupling analysis[M]. Chengdu: Southwest Jiaotong University Press, 2007: 3-13.

Mechanical behavior of constructed underwater tunnelConsidering influence of river water level fluctuation

YUE Jian1,2， TAN Renhua1,2，AN Yonglin1,2，LIU Yunsi1,2

(1.School of Civil Engineering, Hunan University of Science and Technology, Xiangtan 411201, China；2. Hunan Provincial Key Laboratory of Geotechnical Engineering for Stability Control and Health Monitoring,Hunan University of Science and Technology, Xiangtan 411201, China)

The mechanical behaviors of underwater river-crossing traffic tunnels with small clearances that were constructed by the mining method were studied from numerical simulation and field monitoring with the influence of river water level fluctuation taken into account. Firstly, the effects of the river water level fluctuation and the excavation face position on the seepage field and stress field of the surrouding rock were considered. The three-dimensional calculation model was established. According to the variation curve of river water level versus construction step obtained from field monitoring, 92 cases of construction step versus river water level were fed into the model. Then, the calculation results were analyzed with those from numerical simulation and field monitoring compared. Finally, the 8 cases with sharp rise and sharp fall of river water level were calculated and analyzed. The results showed that with the disturbance of adjacent cave construction, the maximum crushing stress of initial lining of upper bench of the cave own appeared in the arch springing; in comparison with the former construction step, the new construction step that was advanced in conjunction with the sudden river level rise of 5m, could significantly exaggerate the force condition of the initial lining near the construction zone. Based on the research findings, some engineering suggestions were put forward.

underwater tunnels with small clear spacing；river water level change；mechanical behavior of construction；mining method

2016-02-20

国家自然科学基金资助项目(51308209；51408216)；湖南省自然科学基金资助项目(2015JJ6038)

岳健 (1978-)，男，山西阳泉人，讲师，博士，从事隧道工程方面的研究；E-mail: changshalaosan@163.com

U459

A

1672-7029(2016)11-2211-09