循环荷载下地铁隧道基底软岩动力变形试验研究

赵丹，曹前，黄娟

(1.长沙市轨道交通集团有限公司，湖南 长沙 410003；2.中南大学 土木工程学院，湖南 长沙 410075)



循环荷载下地铁隧道基底软岩动力变形试验研究

赵丹1，曹前1，黄娟2

(1.长沙市轨道交通集团有限公司，湖南 长沙 410003；2.中南大学 土木工程学院，湖南 长沙 410075)

全风化砾岩是一种受剧烈风化作用形成的低强度软岩。通过对全风化砾岩进行动三轴循环加载试验，对低频循环荷载作用下的不可恢复累积塑性动应变的发展规律进行研究，并分析其受动应力幅值、静偏应力大小、围压影响、荷载频率的影响程度。研究结果表明：岩样的动力变形以临界应力为界，呈现稳定型和破坏型两种发展形式；在循环荷载作用下，全风化砾岩的累积塑性动应变显著影响因素是动应力幅值与静偏应力幅值；围压及荷载频率因素为次要影响因素。岩样的变形发展随轴向动应力和静偏应力增加而增大，并且达到稳定所需的加载时间愈长。

循环荷载；隧道；全风化砾岩；动力变形

全风化砾岩是一种受剧烈风化作用形成的低强度软岩[1]。由于全风化砾岩的强度较原岩或微风化砾岩降低更为显著，当地铁隧道在风化砾岩层中穿越时，全风化砾岩在列车长期反复行车作用下的变形是地铁隧道运营中值得探讨的一个课题。因此，研究全风化砾岩在循环荷载作用下的动力变形发展规律，并从中找出影响变形的主要因素显得非常必要。

近年来，国内外学者针对各地区不同的岩土体在三轴动力试验方面开展了深入的研究[2-15]：刘剑锋等[2-3]对细砂岩采用循环荷载方法研究了岩石阻尼参数、动弹模及动泊松比等动力参数的影响；丁祖德[4]对砂质泥岩的动应变发展规律进行了研究，揭示了砂质泥岩的三阶段变形发展及其破坏模式下的规律及特点；唐益群等[5]通过对上海地铁隧道淤泥质黏土开展室内循环三轴试验，指出累积应变与孔隙水压力发展规律之间存在相似性，并指出动荷载频率越低，累积应变越大。刘增荣等[6]对黄土开展了动力试验，提出了黄土在地铁循环荷载下存在临界动应比。

然而，以往的动力试验多是围绕我国东部沿海地区饱和黏土、砂土而进行的；实际上，由于各地区岩土体本身的组成及性质的不同，动力特性必然存在差异。在我国广大的南方地区，城市轨道交通等地铁隧道普遍在第四系的各类砾岩、粉砂岩等岩层中穿越，本文中的风化砾岩就是其中一种[1]。基于此，本文通过开展室内循环动力三轴试验，结合前人的研究成果，对与动力变形密切相关的因素——动载幅值、静偏应力、围压、加载频率进行了试验研究。

1 试验方法

1.1 试验仪器

试验采用采用微机控制电磁式振动三轴仪DDS- 70。(Dynamic Triaxial Testing Systems)。DDS- 70微机控制电磁式振动三轴试验系统由主机、电气系统、静压控制系统和微机系统等主要部

分组成。其工作原理是将圆柱形土试样置于充气的三轴室内上下活塞之间，通过气体压力对试样施加侧向静压力与轴向动压力。

1.2 试样制备

试验岩样取自长沙地区某地铁施工现场的全风化砾岩层。其上覆盖有杂填土、砂卵石层、中风化砾岩。取样深度为地表以下10 m～25 m范围。全风化砾岩呈红褐色，结构松散，岩芯呈碎屑状、砂状，局部夹中砂，胶结程度极差，手捏易散，其主要物理力学指标如表1所示。采用工程地质钻机XY-100型取试样，从现场取得试样并封存。经室内加工成型的试样尺寸为直径Ф39.1 mm，高为80 mm的圆柱体试件。试样如图1中(a)所示。

(a)试验前；(b)试验后图1 试验前后岩样Fig.1 Rock samples of before and after testing

1.3 敏感试验工况

考虑动应力、静偏应力、围压及加载频率四种因素，并结合敏感性分析方法，对循环荷载下全风化砾岩不可恢复累积塑性变形的差别进行了比较。试验的设置工况见表2。

表1 风化砾岩物理力学指标

表2 全风化砾岩动力试验工况

1.4 试验步骤及加载

先将试样装入三轴仪的压力室内进行固结，轴向应变≤0.05%固结完成。关闭排水开关，对试样轴向进行加循环动力荷载，加载波形为正弦波波形。

设定基本循环加载次数为5 000次。试验中按照1数/次采集数据并存储。对于部分情况，按照岩样应变破坏值5%进行控制，到达设定的动应变值时加载停止。

2 试验结果与分析

2.1 循环加载累积应变发展规律

全风化砾岩在循环动力荷载作用下的应变累积过程存在2种典型情况：稳定型和破坏型。其相应的累积塑性变形发展规律分别如图2和图3所示。其中，当动应力幅值小于临界应力值时表现为稳定型变化曲线，动应力超过临界应力值时表现为破坏型变化曲线。达到设定破坏条件后岩样变形如图1(b)所示。

分析图2和图3可知：

1)当动应力幅值小于临界应力值时，岩样的累积动应变随振动次数的增加，变形发展曲线呈稳定型。 其特点是在循环加载初期，试样变形在加荷初期发展较快；随着循环次数的增加，试样逐渐压密，变形增加趋缓，应变值趋于稳定值。因此从变形速率的角度，又可进一步细分为变形发展初始阶段和变形发展稳定阶段。

2)动应力达到或超过临界应力值情况时，岩样的累积动应变随振动次数的增加，变形快速增长，在很短的时间内动应变超过应变控制值并表现为试样明显鼓起呈现破坏(图1(b))。这与典型的岩石破坏变形依次呈变形初始阶段、变形等速阶段及变形快速增长三阶段规律(图4)存在一定区别[6～9]。

分析原因，主要与全风化砾岩的微观结构组成密切相关。全风化砾岩由于风化程度较为彻底，颗粒间胶结程度极差[1]。当承受的动应力超过临界应力后，变形沿胶结面薄弱处快速发展。特别是试验类别一组中动应力幅值由160 kPa增加至170 kPa后，全风化砾岩总的变形由1.11%发展为如图3中所示的变形，由稳定型转化为破坏型。原岩、微风化岩体呈完整状岩体一般最初由微裂纹、细裂纹扩展经过等速变形阶段最终发展成为破坏型。

全风化砾岩的破坏变形发展与完整状岩石破坏变形三阶段规律既有共性又有不同：由于全风化岩自身完整性较差，吸收能量较小，当承受超过临界应力的动力荷载时，全风化砾岩的破坏变形发展为快速发展阶段，初始阶段和等速阶段缺失。因此，全风化砾岩的破坏变形是岩石三阶段发展模型的特例，根本原因在于与风化砾岩的微观结构密切相关。

3)对全风化岩而言，变形破坏临界应力是客观存在的。在本次全风化岩样试验中，临界动应力为160～170 kPa。

图2 累积变形稳定型Fig.2 Stability cumulative deformation

图3 累积变形破坏型Fig.3 Failure cumulative deformation

图4 累积变形三阶段破坏型Fig.4 Three stages of failure cumulative deformation

2.2 循环动载幅值影响分析

为分析动应力幅值对全风化砾岩累积塑性变形总变形的影响程度，在围压为150 kPa、静偏应力为100 kPa、加载频率为2Hz的条件下，取加载动应力幅值分别为50，80，100，160和170 kPa共5种工况开展对比试验。

图5给出了前4种循环加载情况下的累积塑性应变发展与加载前5 000次的关系曲线，图3给出了第5组动力荷载(170 kPa)作用下破坏型动应变与加载次数前50次加载条件下的关系曲线，图6给出了稳定型与破坏型累积动应变与加载次数前50次加载条件下的关系曲线。

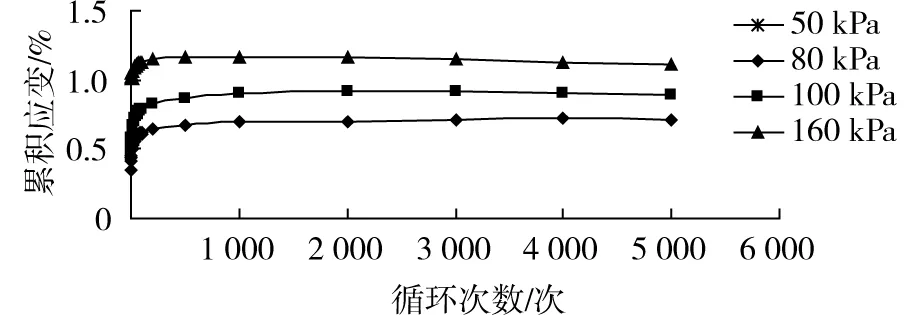
图5 累积稳定变形随循环次数变化曲线Fig.5 Curves of accumulative stable deformation versus cyclic number

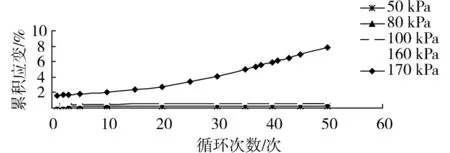
图6 累积变形随循环次数变化曲线Fig.6 Curves of accumulative plastic deformation versus cyclic

从图5和图6中可以得出：

1)动力荷载幅值越大，累积应变越大。对累积应变稳定型发展的前4种工况，岩样的变形在前200次加载时的初始阶段为加速变形，加载200次以后变形趋于稳定。应变的增长速度呈现变形初始阶段和变形稳定两阶段：第一阶段为变形快速增长阶段但变形速率随振次增加逐渐减小，尤其是荷载刚施加的一段时间；第二阶段变形不再增长，增长速率渐趋于0，动应变趋于一个稳定值。

2)动应力幅值对岩样变形影响显著。当动应力小于160 kPa时，动应变曲线总体发展趋势趋于稳定；而当轴向动应力幅值为170 kPa时，动应变随着循环次数的增加，岩样累积变形呈二次曲线形快速发展。岩样最终累积塑性应变达到7.81%而破坏。

3)不同动应力幅值下，岩样对应的塑性累积应变有所不同，对于应变稳定型岩样具体表现为：当动应力幅值为50 kPa时，对应变形呈稳定型。设定循环加载5 000次后其塑性变形已基本趋于稳定，取为总应变量，对应的加载5000次的累积应变为0.357%，而前200次加载的累积应变为0.326%，占总变形量的99.7%；当动应力幅值为80 kPa，前200次加载、5 000次加载的累积应变分别为0.646%和0.708%，初始变形阶段占总变形量的91.2%；当动应力幅值为100 kPa时，相应累积应变分别为0.826%和0.895%，初始变形阶段占总变形量的92.2%；当动应力幅值为160 kPa时，相应累积应变分别为1.11%和1.17%，初始变形阶段占比总变形量的94.8%。可见，初始阶段循环作用下产生的动力应变略占累积总应变的90%以上，并且随着动应力幅值的增加，初期循环作用产生的累积应变占总应变的比重逐渐减少。

2.2 静偏应力影响分析

在围压为150 kPa、动应力幅值为75 kPa、加载频率为2 Hz等压固结的试验因素下，开展了静偏应力分别为0，50，75，90和150 kPa五种水平的循环加载试验。图7为典型工况下的累积轴向应变与振动加载循环次数前5 000次的关系曲线。

图7 不同静偏应力下累积变形随循环次数变化曲线Fig.7 Curves of accumulative plastic deformation versus cyclic number under different static deviator stress

从图7可知：

1)该组岩样的累积轴向动应变随振次的增加最终表现为稳定型。静偏应力分别为0，50，75，90和150 kPa条件下的累积塑性应动应变值分别为0.581%，0.568%，0.814%，0.907%和1.75%。对于相同的动应力幅值，在不同静偏应力条件下，静偏应力越高时，岩样产生的累积塑性动应变越大。

静偏应力150 kPa与静偏应力为0 kPa加载条件下相比，累积塑性动应变增加了2.02倍，静偏应力对岩样的累积变形影响比较明显。

2)静偏应力分别为0，50，75，90和150 kPa时对应的前200次占总的累积变形量为99.9，99.4，94.7，92.2和87.0%。可知，静偏应力越大，达到稳定的变形值所需加载的振次越多，所需加载的时间越长，且该种影响随偏应力的增大而愈加明显。

3)静偏应力越大，岩样在相同的动应力幅值加载条件下，达到稳定所需要的时间也越长，岩样在动应力加载条件下，静偏应力会促进岩样内部裂隙的发展，产生不可恢复的塑性变形，因此静偏应力对总变形存在时间效应。

2.3 围压影响分析

在动应力幅值为200 N、固结比为1.0，动载频率为2 Hz的试验因素下，开展围压分别为150，200，300和400 kPa的循环加载试验。图8给出了不同围压水平下岩样的累积塑性应变随振动加载循环次数的变化情况。

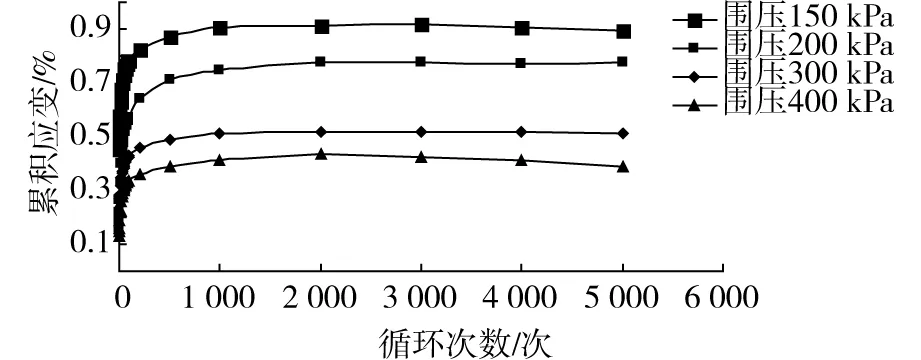
图8 不同围压下累积塑性变形随循环次数变化Fig.8 Curves of accumulative plastic deformation versus cyclic .number under different confining pressure

从图8分析，围压分别为150，200,300和400 kPa时对应的累积变形对应为0.895%，0.774%，0.509%和0.391%。围压每增加100 kPa，累积变形相应减少0.11%～0.17%。试样在相同振次下的累积塑性应变值随围压的增加而减小。对应的原因是在相同的固结比条件下，围压越大，对应的轴压越大，试样三向受力越大，在加载的初期会促进岩样裂隙一定程序的密闭。岩样的物理力学性能上表现为动弹性模量越大，因此在相同的动载作用下产生应变越小。

可见，随着围压的提高，在循环动应力条件下，岩体裂隙变形的发育减缓，另一方面岩体本身风化程度减弱，岩体完整性较好，进一步阻碍了变形的发展。因此，从基底围岩的长久变形方面分析，加大线路在岩层中的埋深对提高隧道稳定是有利的。

2.4 荷载频率影响分析

荷载的频率主要是结合隧道上部列车的运营情况选取了0.5～5 Hz频段，共开展(a)(b)两种工况进行。(a)组的试验条件为：动载200 N、围压150 kPa、固结比1.0、静偏应力100 kPa，荷载频率分别为1，2和5 Hz。(b)组的试验条件为：动载150 N、围压150 kPa、静偏应力0 kPa，荷载频率分别为0.5，2和5 Hz。

实验结果如图9及图10所示。从试验结果可知：

(a)组试验，加载前50振次对应的累积塑性应变分别为0.552%，0.432%和0.432%；加载5 000振次对应的累积塑性应变分别为0.731%，0.481%和0.512%。 (b)组试验，加载50振次对应的累积塑性应变分别为0.593%，0.668%和0.592%；加载5 000振次对应的累积塑性应变分别为0.722%，0.581%和0.527%。可见，随着荷载频率的提高，相同振次条件下的累积塑性应变略有减小。

在试验选取的0.5～5 Hz低频段范围内，荷载频率为1 Hz时，试样产生的塑性应变最大，但在此频率范围内岩样的累积塑性总应变小于0.8%，各频率作用下的变形差别较小。

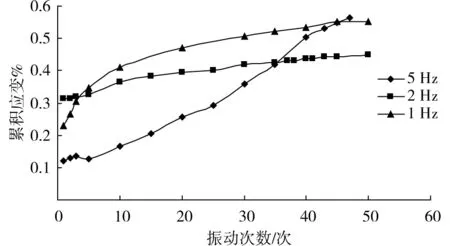
图9 静偏应力100 kPa加载下风化砾岩样的变形随循环次数变化曲线Fig.9 Curves of accumulative plastic deformation σs=100 kPa versus cyclic number

图10 静偏应力0 kPa加载下风化砾岩样的变形随循环次数变化曲线Fig.10 Curves of accumulative plastic deformation under σs=0 versus cyclic number

3 结论

1)通过比较不同因素对岩样的轴向累积应变的影响，动应力幅值对全风化砾岩变形影响显著。当应力幅值小于临界应力时，轴向累积应变曲线为稳定型；当应力幅值高于临界应力时，变形发展很迅速，变形曲线基本呈抛物线形发展。这与一般的岩石破坏变形呈三阶段规律即有共性又有不同，其变形的发展与风化岩的微观结构密切相关。

2)对于稳定型变形曲线，根据变形速率的快慢，分为初期阶段和稳定阶段。全风化砾岩的初期阶段变形占总变形量的90%以上，并且随着动应力水平的提高，初期循环作用阶段产生的应变量占总的累积应变的比例有所减小。

3)静偏应力对全风化砾岩的变形影响较大，在其它影响因素相同的情况下，静偏应力由0 kPa增加到150 kPa时，总应变增加了2.02倍。并且随着轴向静偏应力增加，岩样趋于稳定阶段所需的加载时间愈长。

4)相比较于动应力幅与静偏应力幅，围压及加载频率两个因素对累积动力变形影响较小。围压越高，由于越能抑制岩样加载初期裂隙发展，岩体总变形随之减小。在0.5～5 Hz内加载频率范围内，各频率对总变形差别不到0.2%。其中以循环荷载为1 Hz的情况对应产生的累积变形最大。

[1] 彭柏兴,刘颖炯,刘毅.红层溶蚀风化特征及其工程影响[J]. 岩土工程学报,2011,33(增1):141-145. PENG Baixing, LIU Yinjiong, LIU Yi, et al. Corrosion and weathered characteristics and engineering infulences of red bed[J]. Chinese Journal of Geotechnical Engineering. 2011,33(Suppl 1):141-145.

[2] 刘建锋,谢和平,徐进，等.循环荷载下岩石变形参数和阻尼参数探讨[J]. 岩石力学与工程学报,2012,31(4):770-777. LIU Jianfeng, XIE Heping, XU Jing， et al. Discussion on deformation and damping parameters of rock under cyclic loading[J]. Chinese Journal of Rock Mechanics and Engineering,2012,31(4):770-777.

[3] 刘建锋,谢和平,徐进,等.循环荷载下岩石阻尼特性的试验研究[J]. 岩石力学与工程学报,2008,27(4):712-717. LIU Jianfeng, XIE Heping, XU Jing， et al. Discussion on deformation of rock under cyclic Loading[J]. Chinese Journal of Rock Mechanics and Engineering, 2008,27(4):712-717.

[4] 丁祖德.循环荷载作用下富水砂质泥岩变形特性研究[J]. 岩土工程学报,2012,34(3):534-538. DING Zude .Experimental study on dynamic deformation behaviors of water-rich sandy mudstone under cyclic loading[J]. Chinese Journal of Geotechnical Engineering, 2012,34(3):534-538.

[5] 唐益群,李珺,刘莎,等.地铁行车荷载作用下淤泥质黏土累积特性的试验研究[J].工程地质学报.2011,19(4)460-466. TANG Yiqun， LI Jun, LIU Sha, et al. Experimental study on the behavior of muddy clay under subway loading[J]. Journal of Engineering Geology, 2011,19(4)：460-466.

[6] 刘增荣,王鑫.地铁振动下黄土永久变形力学模型的研究[J].西北工业大学学报，2011,29(4)：587-593. LIU Zengrong, WANG Xin. A mechanical model of loess permanent deformation under metro vibration[J]. Journal of Northwestern Polytechnical University, 2011,29(4):587-593.

[7] 黄茂松,李进军,李兴照.饱和软粘土的不排水循环累积变形特性[J].岩土工程学报,2006,28(7):891-895. HUANG Maosong, LI Jinjun, LI Xingzhao. Cumulative deformation behaviour of soft clay in cyclic undrained tests[J]. Chinese Journal of Geotechnical Engineering, 2011，29(4)：587-593.

[8] 唐益群,黄雨,叶为民,等.地铁列车荷载作用下隧道周围土体的临界动应力比和动应变分析[J]. 岩石力学与工程学报，2003,22(9):1566-1570. TANG Yiqun, HUANG Yu, YE Weiming, et al. Critical dynamic stress ratio and dynamic strain analysis of soils around the tunnel under subway train loading[J]. Chinese Journal of Rock Mechanics and Engineering, 2003,22(9):1566-1570.

[9] 王常晶,陈云敏.交通荷载引起的静偏应力对饱和软黏土不排水循环性状影响的试验研究[J]. 岩土工程学报,2007,29(11) :1742-1747. WANG Changjing, CHEN Yunmin. Study on effect of traffic loading induced static deviator stress on undrained cyclic properties of saturated soft clay[J]. Chinese Journal of Geotechnical Engineering. 2007,29(11) :1742-1747.

[10] 张勇,孔令伟,郭爱国,等.循环荷载下饱和软黏土的累积塑性应变试验研究 [J]. 岩土力学,2009,30(6) :1542-1548. ZHANG Yong, KONG Ningwei, GUO Aiguo, et al. Cumulative plastic strain of saturated soft clay under cyclic loading[J]. Rock and Soil Mechanics. 2009,30(6) :1542-1548.

[11] 丁祖德, 彭立敏.高速铁路隧道列车振动响应影响因素分析[J].铁道科学与工程学报, 2011, 8(4):1-6. DING Zude, PENG Limin. Analysis of influence factors on vibration response of high speed railway tunnel[J]. Journal of Railway Science and Engineering. , 2011, 8(4):1-6.

[12] 刘晓红,杨果林,方薇.武广高铁无碴轨道路堑基床长期动力稳定性评价[J].中南大学学报(自然科学版), 2011, 42(5): 1393-1398. LIU Xiaohong, YANG Guolin, FANG wei. Long-term dynamic stability evaluation of cutting bed under ballastless track of wuhan-guangzhou high-speed railway[J]. Journal of Central South University(Science and Technology, 2011, 42(5): 1393-1398.

[13] Forrest J A, Hunt H E M. Ground vibration generated by trains in underground tunnels[J]. Journal of Sound and Vibration, 2006, 29 (4): 706-736.

[14] Hussein M F M, Hunt H E M. A numerical model for calculating vibration from a railway tunnel embedded in a full-space[J]. Journal of Sound and Vibration, 2007, 305(2): 401-431.

[15] Yang Y B, Hung H H. Soil vibrations caused by underground moving trains[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2008, 134(1): 1633-1644

Dynamic deformation of soft rock under cyclic loading in subway tunnel basal

ZHAO Dan1, CAO Qian1, HUANG Juan1

(1. Changsha Metro Group CO.,Ltd, Changsha 410003, China;2. School of Civil Engineering Central South University, Changsha 410075, China)

Weathered-conglomerate is a low-strength soft rock formed by intense weathering of a subway tunnel basement. Using dynamic triaxial cyclic loading test, the law of development of dynamic strain for weathered conglomerate under cyclic loading was studied, while the influence degree of dynamic stress amplitude, static deviator stress, confining pressure impact and loading frequency on dynamic strain for weathered conglomerate was analyzed. The results showed that, the deformation development of weathering conglomerate could be divided into two categories, i.e., stable and failure. Under cyclic loading, the significant factors affecting plastic dynamic strain were the dynamic stress and static deviator stress amplitude, whereas confining pressure and load frequency were secondary factors. The rock deformation increased with the axial dynamic stress and static deviator stress, and greater number of load applications is needed for reaching stable state.

cyclic loading; tunnel; weathered-conglomerate; dynamic deformation

2016-01-20

国家自然科学基金资助项目(51508575，51108461)；长沙市建设科技资助项目

赵丹(1982-) )，女，湖南长沙人，高级工程师，博士，从事结构与地下工程方面的设计及施工管理工作；Email: rachelcsu@163.com

TU311.3

A

1672-7029(2016)11-2204-07