基于RBF神经网络的液压泵特性建模研究

倪 红，叶建华，江吉彬

(1.福建船政交通职业学院 汽车运用工程系，福建 福州 350007；2.福建工程学院 机械与汽车工程学院，福建 福州 350118)



基于RBF神经网络的液压泵特性建模研究

倪 红1，叶建华2，江吉彬2

(1.福建船政交通职业学院 汽车运用工程系，福建 福州 350007；2.福建工程学院 机械与汽车工程学院，福建 福州 350118)

影响液压泵特性的因素多、关系复杂、呈现出高度的非线性，难以进行数学建模。本文采用RBF(Radial Basis Function，径向基函数)神经网络对液压泵流量特性、功率特性、效率特性进行建模，以定量叶片泵FA1-11-FR为试验对象，利用聚类法确定基函数的中心，根据最小二乘法计算连接权值，构建了流量、功率特性模型和液压泵特性综合模型，并通过实例验证，用一定量的实测数据就能获得液压泵的性能全貌，网络模型精度好，泛化能力强。

液压泵；神经网络；液压泵特性；径向基函数

液压泵是液力系统的动力元件，它将输入的机械能转换成液压能，为整个液力系统提供动能。液压泵的特性，是液压系统设计的一个重要参考依据，直接影响液压系统的工作性能和可靠性。然而，液压泵的特性不仅与泵的结构直接相关，还受工作压力、转速、工作液的粘度和液压泵的磨损程度的影响，呈现出高度的非线性[1]，为了获得液压泵的特性，一般需要在不同工况下进行大量的试验，并分析整理实验数据。叶敏等[2]基于液压试验台研究了液压泵的特性，并进行了数据分析。邢科礼等[3]利用计算机采用等值线、移动最小二乘法等方法进行特性曲线的拟合绘制。丁问司等[4]则借助AMESim软件进行了正弦液压泵的建模与仿真。

传统方法需要大量的实验数据，并且耦合因素多，结果呈现高度的非线性，难以通过数学建模的方式描述其特性。人工神经网络通过模拟人脑神经元结构，具有学习、推理、辨别能力，在强耦合、非线性建模方面具有优势。杨会菊与彭熙伟等[5]将BP(Back Propagation，误差反向传播)神经网络引入到液压泵的特性建模上，取得了较好的效果。与BP神经网络相比，RBF神经网络的拓扑结构更加紧凑, 学习的收敛速度更快，泛化能力更强，可映射任意复杂的非线性关系，拥有唯一最佳逼近的特性[6]。因此，本文利用少量的试验数据，采用RBF神经网络建构液压泵的特性模型，以定量叶片泵FA1-11-FR为对象，对构建的RBF神经网络模型的精度、泛化能力等进行验证。

1 液压泵特性

在工作过程中，影响液压泵性能的因素有很多，通常用液压泵的流量特性、功率特性与效率特性表征液压泵的性能，其中效率特性又包括容积效率、机械效率与总效率。

液压泵的实际流量q随出口工作压力p的变化用流量特性表征。液压泵出口工作压力p的大小取决于负载和管路的压力损失。液压泵的实际流量q则取决于液压泵的理论设计排量V、泵轴转速n和液压泵的流量损失Δq，即q=Vn-Δq，其中Δq是液压泵的流量损失。它是由以下两方面原因引起的：1)液压泵在工作过程中受高压的作用引起内部流量的泄露、油液的压缩；2)受吸油阻力、油液粘度和液压泵的高转速的影响使工作液不能充满密封工作腔[7]。

用容积效率ηv表征液压泵在工作中流量损失Δq情况，可表示为：

(1)

容积效率ηv随着液压泵工作压力的增大而减小，且随液压泵的结构类型不同而异。

泵轴输入功率Pr随出口工作压力p的变化用功率特性进行表征。液压泵用于实现机械能向液压能的转换，输入功率Pr为驱动液压泵主轴上的机械功率，输出功率Po为液压泵输出的液压功率。输出功率Po可用实际流量q与口工作压力p的乘积表示，即Po=pq。实际输出功率Po与输入功率Pr的比值则为液压泵的总效率η，即：

(2)

液压泵的机械效率ηm表征液压泵在工作过程中的机械损失。机械损失是液压泵能量损失的主因，由于液压泵体各相对运动件间的机械摩擦和液体粘性而会引起摩擦损失[7]，可用液压泵的理论转矩与为实际输入转矩的比值进行表征，也可以通过总效率与容积效率计算得到：

(3)

在液压泵特性评定过程中，涉及工作压力p、液压泵的排量V、主轴转速为n、实际流量q、输入功率Pr等参量。其中液压泵的排量V是一个常量，大小仅与液压泵的结构和几何尺寸有关。而其他参量除与液压泵的结构、几何尺寸、运动方式有关，还与系统状态相关、受多因素影响，呈现高度的非线性，难以通过数学建模的方式计算，而需要通过大量的试验进行评定。

2 基于RBF神经网络的建模方法

RBF神经网络是一种性能优良的三层前馈型神经网络，可映射任意复杂的非线性关系，理论证明在前向网络中RBF网络是完成映射功能的最优网络。采用RBF神经网络进行液压泵特性的建模，则只需利用有限的数据，就能很好地映射液压泵特性参量间的非线性关系，实现最佳逼近。

如图1所示，RBF神经网络由输入层、隐含层和输出层组成。X=[x1，x2，…，xi，…，xg]T为神经网络的输入，维数g由液压泵特性的输入向量个数决定。Y=[y1，y2，…，yk，…，yl]T为神经网络的输出，维数l为液压泵特性的输出向量个数决定。输入层起到与外界连接的作用。RBF神经网络只有一个隐含层，由一组径向基向量构成高维的隐空间Y=[R1，R2，…，Rj，…，Rm]T，实现X→Rj(x)非线性映射。本文采用高斯函数f(x)=e-(x/σ)2为隐含层的径向基函数。输出层则对输入提供响应，实现Rj(x)→Y线性映射。

图1 网络的神经系统结构

网络的前向计算过程为：

(1)先计算输入与基函数中心距离，然后根据距离进行非线性变换。隐藏层第j个神经元的传递函数：

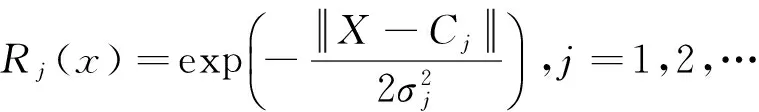
(2)输出层为隐含层的线性加权，第k个神经元网络输出为：

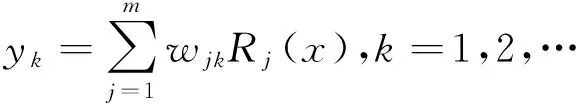
式中：wjk为隐藏层第j个神经元与输出层第k个神经元的连接权值。

RBF的训练过程分两步：第一步确定基函数的中心Cj和基宽参数σj为无教师学习；第二步，确定连接权值向量Wj=[wj1，wj2，…，wjk，…，wjl]T，j=1，2，…m;为有教师学习。

第一步，基于k-means聚类的无教师学习过程为：首先，随机选取的m个训练样本作为初始聚类中心；然后，计算所有N个输入样本与聚类中心的距离，并按近邻规则进行归类，获得A(t)聚类集合，t为迭代次数；接着，将聚类集合Aj(t)中样本的平均值作为新的聚类中心Cj(t+1)，重新依据距离进行归类，直至聚类中心不在变化为止，Aj(t)为第j个中心的聚类集合。根据确定的聚类中心，计算第j个数据中心与其他最近中心的距离dj，然后根据dj，确定基宽参数σj=Kdj，K为重叠系数。

第二步，根据被激活的隐含层采用最小二乘法计算连接权值向量。设E为样本的输出误差，则E可用如下公式计算：

通过偏差最小进行权值的调节，可得权重的迭代公式为：

3 液压泵的特性建模与验证

3.1 流量特性和功率特性建模

泵的实际流量q随工作压力P的变化为流量特性，泵轴输入功率Pr随出口工作压力P的变化为功率特性。这两个特性建立的是工作压力P与实际流量q、泵轴输入功率Pr的关系。RBF神经网络可以建立起工作压力与实际流量q、泵轴输入功率Pr的复杂非线性关系，并且能利用少量的试验数据作为网络的训练样本，通过迭代学习建构起泛化能力强稳健模型，从而可以计算出任一输入所对应的输出。

流量、功率特性的输入为工作压力P，输出分别为实际流量q和泵轴输入功率Pr。相应地构建的RBF网络输入层神经元个数为1，用于工作压力P的输入，工作压力P在取值范围内进行归一化处理。输出层神经单元为2，用于输出实际流量q和泵轴输入功率Pr。隐含层单元个数的确定是RBF神经网络的关键，本文通过动态循环增加的方式确定：从0开始，不断增加隐含层单元个数，逐步检查输出误差是否满足误差要求，直到满足要求为止。重叠系数K决定了神经元响应输入的范围，太小会造成神经元响应区域欠交叠，不能有效地覆盖输入区域，太大则可能引起重复响应，通过多次试验确定。这里以定量叶片泵FA1-11-FR为对象，表1记录了试验测量得到的12组用于液压泵流量与功率特性网络的训练数据。

表1 液压泵流量与功率特性训练数据

图2是重叠系数K=4时，用表1数据进行训练时的误差性能曲线图。可以看出网络隐含层个数增加到10个时，网络的均方误差达到5.88×10-6，满足期望误差1×10-5的要求，网络停止训练。表2记录了训练后RBF神经网络模型得到的预测值与试验测量值，可知，流量的预测均方值误差为0.00216，相对误差的最大值为0.37%，功率的预测均方值误差为0.0065，相对误差的最大值为0.92%，说明构建的RBF神经网络模型具有很好的泛化能力，利用有限的训练样本就能得到液压泵流量与功率特性的全貌数据。

图2 训练误差曲线

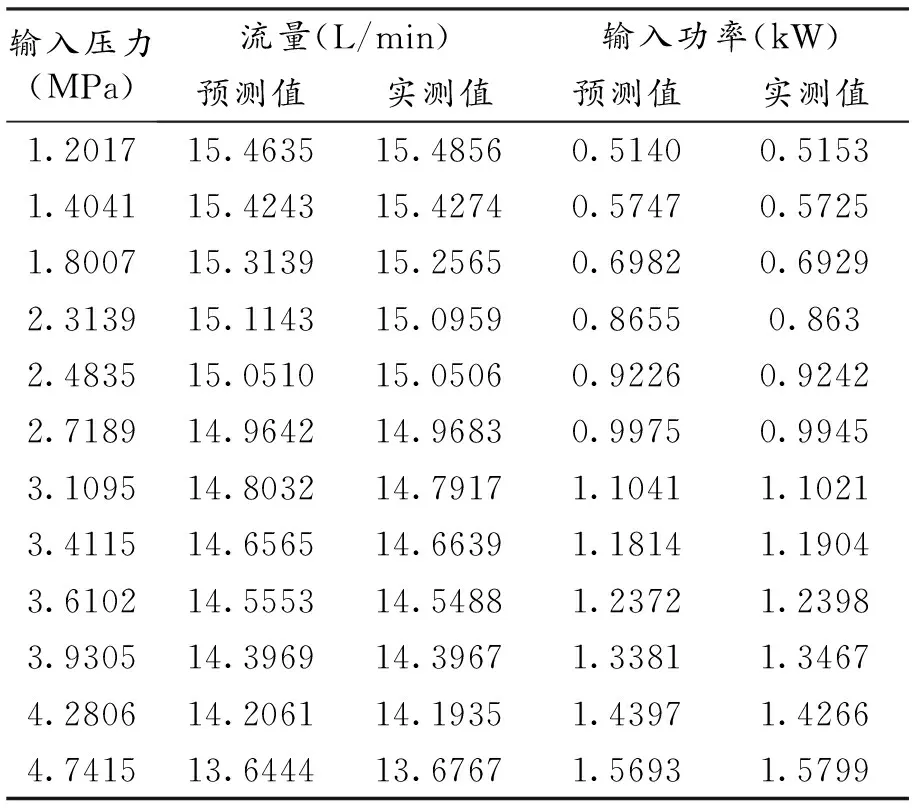
表2 液压泵流量与功率特性预测值与实测值对照表

3.2 综合特性建模

上面的流量特性和功率特性模型，可得工作压力p与实际流量q、输入功率Pr的关系。结合主轴转速n和液压泵的排量V，利用公式(1)～(3)，可计算出液压泵的容积效率ηv、机械效率ηm和总效率η等效率特性。根据实测的主轴转速n和定量叶片泵FA1-11-FR的理论排量V：11 mL/r，利用表2数据可将误差控制在1%以内。

RBF神经网络也能对上述的映射与效率计算过程进行统一建模。构建的RBF神经网络的输入则为通过归一化后的工作压力p和主轴转速n，由于液压泵的排量V为常数，不作为输入向量。输出则为实际流量q、输入功率Pr、总效率η，容积效率ηv。机械效率由(3)式计算。

表3 液压泵综合特性预测值与实测值对照表

表3是通过RBF神经网络统一建模后的预测值与试验测试数据的对比参照表。流量的相对误差都在0.5%以内，输入功率的相对误差在1.5%以内。与上一网络相比，由于网络结构参量的增加，映射关系和拓扑结构越加复杂，网络精度有所下降，但依然保留了较高的精度。总效率η预测的相对误差在1.5%以内，而容积效率ηv则在0.3%以内。

4 结论

本文在分析液压泵特性及其影响因素的基础上，研究了RBF神经网络的建模原理与实现过程。以定量叶片泵FA1-11-FR为对象，进行了液压泵流量特性和功率特性的建模，以及综合流量特性、功率特性的映射关系和容积效率、机械效率、总效率计算过程的统一建模，并且通过实例验证了建模的可行性和模型的计算精度。同时表明了，利用少量试验的测试数据对RBF神经网络进行训练，就能建立起鲁棒性好、精度高、泛化能力强的复杂非线性映射关系，从而能获得液压泵特性的全貌，为液压泵特性曲线的构建提供新方法，能大量减少测试的时间和强度。

[1] Herzog S, Neveu C, Placek D. The benefits of maximum efficiency hydraulic fluids[J].Machinery Lubrication，2005，7: 7-16．

[2] 叶敏，易小刚，蒲东亮，等.液压泵效率与排量特性试验研究[J].中国工程机械学报， 2013， 11(2):157-161．

[3] 邢科礼，纪铭，金侠杰，等.移动最小二乘法在液压泵/马达特性曲线绘制中的应用[J].机床与液压，2007，35(5)：140-142．

[4] 丁问司，张旭.正弦液压泵建模与仿真[J].机床与液压， 2012， 40(6):25-30．

[5] 彭熙伟，杨会菊.液压泵效率特性建模的神经网络方法[J].机械工程学报，2009，45(8):106-111．

[6] Wu J D，Liu J C.A forecasting system for car fuel consumption using a radial basis function neural network[J].Expert Systems with Applications，2012，39(2)：1883-1888．

[7] 李壮云.液压元件与系统[M].武汉：华中科技大学出版社，2008．

(责任编辑：熊文涛)

2016-09-14

国家自然科学基金项目(51575110)；福建省科技区域发展项目(2016H4006)

倪 红(1969- )，女，福建福清人，福建船政交通职业学院汽车运用工程系副教授，硕士。

叶建华(1980- )，男，福建宁德人，福建工程学院机械与汽车工程学院副教授，福州大学博士研究生。

TP137

A

2095-4824(2016)06-0113-04