液氮管道排空过程CFD模拟及分析

陈 虹 邹 阳 梁文清 钱 华 高 旭

(1总装备部工程设计研究总院航天低温推进剂技术国家重点实验室, 北京 100028)(2东南大学能源与环境学院, 南京 210096)



液氮管道排空过程CFD模拟及分析

陈 虹1邹 阳2梁文清2钱 华2高 旭1

(1总装备部工程设计研究总院航天低温推进剂技术国家重点实验室, 北京 100028)(2东南大学能源与环境学院, 南京 210096)

为研究低温管路中低温液体的排空过程,采用计算流体力学(CFD)方法中非稳态流动以及流体体积(VOF)模型对管路中液氮向外排空过程进行模拟计算,并将模拟结果与实验结果进行对比验证.模拟结果显示,当氮气质量流量较小时,氮气虽然会在一定时间内到达出口,但管道底部仍存有液氮,出现分层现象.这就需要通过氮气带进的热量使液氮受热蒸发排空,致使完全排空时间变长.随着氮气质量流量的增大,排空时间变短.当氮气流量增加到一定数值时,管道底部无液氮残留,可以直接完全排空.该研究结果可以同时为排空低温液氢等危险流体提供理论指导.

管路排空;低温液体;数值模拟;流体体积

随着低温技术的发展,低温液体产品已在国民经济、国防、科学研究等众多领域中发挥着重要作用.在低温管路中,低温液体如液氢、液氧、液氮等在加注完成后,加注管道内会存有低温液体.对于一些比较复杂的管路,液体无法靠自身重力排出管道,一般采用向管内注入常温气体的方法将低温液体排出管路.气体注入会推动低温液体运动,同时由于气体为常温,所以会加热低温液体,使与气体接触的低温液体气化从而加快低温液体的排空过程.进行低温流体管路排空实验时,无法对管路内流动现象进行直接观测,只能观测出口处的排放情况,利用数值模拟方法可以增加对低温液体管路排空现象规律的认识和理解.

文献[1]研究了不同气体体积分数以及不同速度情况下液氢向外排放过程,主要关注液氢排出管道后在外界的流动情况.文献[2]研究了在低质量和热流条件下接近水平的液氮和液氢两相流动模型.文献[3]建立液氮在垂直圆管内流动沸腾过程模型,并进行了数值模拟.文献[4]对液氮的沸腾进行了CFD模拟,同时通过可视化实验与模拟结果进行对比验证.文献[5]对贮箱内低温推进剂气化进行CFD模拟,研究箱内传热传质情况.本文基于研究现状与实际问题,为了直观地观察管道中低温液体在排空过程以及流动规律,利用氮气和液氮来模拟低温管道中的排空过程,采用CFD方法对管内低温液体的流动过程进行仿真.

1 物理模型

本文研究的管道如图1所示.管道直径为0.1 m,左侧为进口,高度为2.0 m,右侧为出口,高度为2.2 m.管外包有保温材料,假设管道与外界环境无热量交换.选取液氮作为低温液体介质,同时选取常温氮气作为气源.氮气通过左侧管道的进口注入管道内.在初始时刻t=0 s时,假设管道内充满液氮,管内液氮的平均温度为77 K,通入氮气的平均温度为298 K.氮气从进口充入管道内会推动液氮向前流动,同时由于氮气温度远高于液氮温度,故在氮气与液氮的接触面上氮气会加热液氮使之气化,产生气液两相氮.液氮的气化使液氮量减少,从而进一步减少管内的液氮量.主要物理过程为氮的多相流动过程和氮的相变过程.

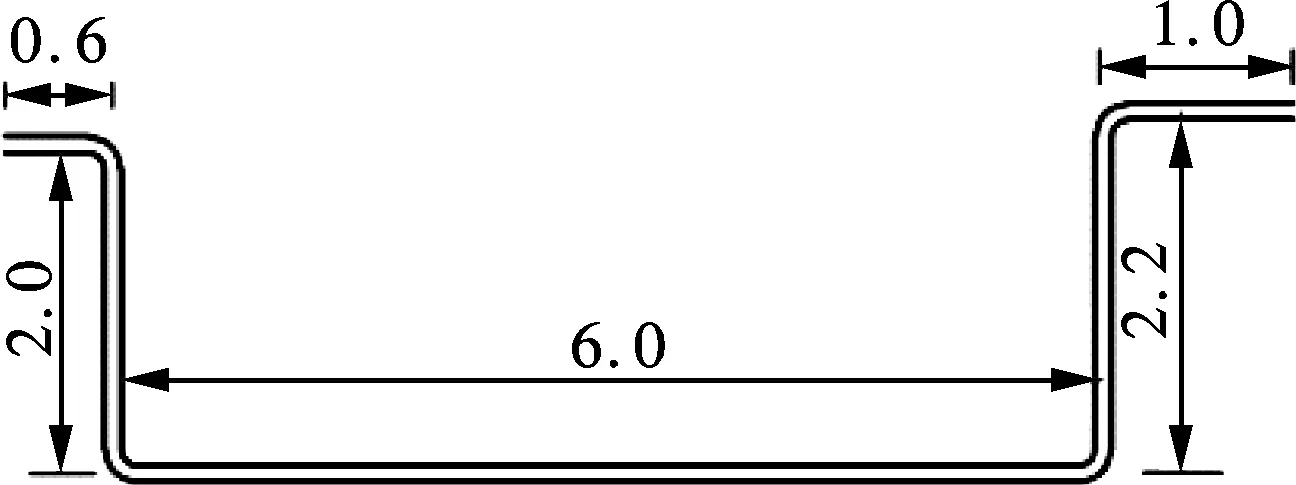
图1 管道示意图(单位:m)

2 数学模型

为满足仿真需要,低温管道的数学模型除了包括多相流的通用控制方程外,还需要建立相变的蒸发冷凝模型.

2.1 多相流控制方程

关于多相流的计算有3种欧拉多相流模型,即VOF(volume of fluid)模型、混合(mixture)模型和欧拉(Eulerian)模型.可以选取VOF模型来追踪相界面.VOF模型根据各个时刻流体在网格单元中所占体积分数α来构造和追踪自由面.若在某时刻网格单元中α=l,则说明该单元全部为指定相流体;若α=0,则该单元全部为另一相流体,相对于前相流体则称为空单元;当0<α<1时,则该单元为包含两相物质的交界面单元[6].

1) 连续性方程

(1)

式中,αl为液相的体积分数;ρl为液相的密度;ul为液相的速度矢量;Sm为质量源项,表示气液相间传质过程引起的单位体积质量交换率.

2) 动量方程

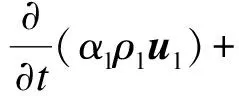
(2)

式中,P为流体压力;[τl]为应力张量.

3) 能量方程

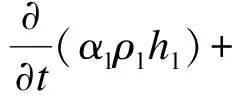
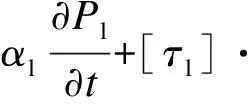
(3)

2.2 蒸发冷凝模型

当低温液体被加热时,若温度高于沸点温度,则液体会气化蒸发.当蒸汽温度低于饱和气体温度时,蒸汽会冷凝成液滴.由于置换气体温度远高于低温液体温度,低温液体会被加热产生气化.

根据Lee[7]的模型,当液体温度大于饱和温度时,有

(4)

式中,mlv为液体蒸发变为气体的质量;c为控制相变强度因子;Tl为液体温度;Tsat为液体饱和温度.

当气体温度小于饱和温度时,有

(5)

式中,mvl为气体冷凝变为液体的质量;αv为气相的体积分数;ρv为气相的密度;Tv为气体温度.

以上2种情况所对应的能量传递分别为

Qlv=mlvq

(6)

Qvl=mvlq

(7)

式中,Qlv为蒸发时的传递热量;Qvl为冷凝时的传递热量;q为气化潜热.

de Schepper等[8]采用模型(1)～(7)对换热管内的沸腾过程进行了模拟,取c=0.1 s-1;Alizadehdakhel等[9]对热管内的蒸发冷凝现象进行了计算,取c=0.1 s-1;Yang等[10]对水平盘管内R141B沸腾流动进行模拟,取c=100 s-1. 由于液氮的相变强度控制因子与水和R141B都不同,且蒸发强度与沸腾过程强度相比较小,同时参考实际实验情况,本文计算选取c=0.01 s-1.

3 网格划分与计算方法

3.1 网格划分

通过Gambit软件建立管道三维仿真模型.模型网格为流体区域,对靠近壁面的流体区域进行网格加密.将模型网格划分为六面体结构化网格,管道圆面网格采用O-Block方法进行划分,体网格采用Cooper方法进行划分,网格数量为8.19×105.划分结果符合网格独立性验证.局部网格划分如图2所示.

(a) 管道截面网格

(b) 管道弯管处网格

3.2 计算方法

模拟计算选用Fluent软件.初始时管内充满液氮,液氮初始温度为77 K,通入氮气的温度为298 K,氮气质量流量分别为5,10,20和30 g/s.流动类型为非稳态流动,湍流模型选择标准k-ε模型.选择基于压力的求解器,速度压力耦合选用SIMPLE算法,选择VOF多相流模型,相变模型中的质量项和能量项通过UDF(user defined function)编译的形式加入计算方程中进行求解.经多次比较,时间步长取为0.1 s,总步长为2 000步.当数值计算的连续性方程、动量方程、能量方程的残差分别为10-4,10-6,10-6量级时,认为计算收敛.

4 计算结果与分析

4.1 氮气质量流量对流动的影响

初始时刻管内充满液氮,经过一段时间的氮气充入,管内流动为气液两相流.图3(a)、(b)为氮气质量流量mN2=5 g/s时各个时间管内气相的分布情况.当t=20 s时,进入的氮气已经到达出口处,但管道底部留有液氮;当t=60 s时,管道底部剩余少量液氮;随着时间的推移,当t=80 s时,管内几乎全部为氮气.从流动过程可以分析得到,由于重力的原因,当氮气质量流量较小时,管内有明显的分层现象,管道底部存有液氮.氮气不能将管道内的液氮全部排出.随着时间的推进,氮气能够加热液氮使之汽化从而全部排空液氮.当氮气质量流量为10 g/s时,不同时间管内气相分布如图3(c)、(d)所示,排空时间约为30 s.当氮气质量流量为20 g/s时,各个时间管道内氮气分布如图3(e)、(f)所示.当t=13 s时,从进口进入管道的氮气已经到达出口处,管道底部无液氮.当t=17 s时,管内几乎全部为氮气.当氮气质量流量为30 g/s时,各个时间管道内氮气分布如图3(g)、(h)所示.当t=12 s时,从进口进入管道的氮气到达出口处,同时管内几乎全部为气体.当氮气质量流量为30 g/s时,不同时刻的温度和速度分布如图4和图5所示.在图4(b)中,出口处管内最低温度为220 K,且管道其他部分温度都高于出口温度,此时可认为完成排空.由图5(a)、(b)对比可以看出,随着管内液氮的减少,流速越来越大.

(a) mN2=5 g/s，t=20 s

(b) mN2=5 g/s，t=60 s

(c) mN2=10 g/s，t=10 s

(d) mN2=10 g/s，t=20 s

(e) mN2=20 g/s，t=5 s

(f) mN2=20 g/s，t=15 s

(g) mN2=30 g/s，t=5 s

(h) mN2=30 g/s，t=10 s

(a) t=5 s

(b) t=10 s

(a) t=5 s

(b)t=10 s

通过计算比较发现,不同的氮气质量流量会对管道底部存有的液氮量产生影响.当氮气质量流量较小时,管道底部会有液氮残留,存在明显的分层现象(见图3(a)),残留的液氮需要被氮气加热气化后才能进一步排空.当氮气质量流量变大时,管道底部的液氮被吹走排空.因此,对于复杂管路,较大的氮气质量流量可以排出管道内的液氮.液氮的排空模拟计算对液氢、液氧以及其他低温液体的排空具有指导意义.

4.2 氮气质量流量对排空时间的影响

当氮气质量流量较小时,需要较长的排空时间.在进口氮气已达到出口处时,若管道底部仍有液氮,氮气无法将液氮全部排出,需要较长的时间对液氮进行加热气化以排空管道.随着氮气质量流量的增大,排空时间逐渐减小,管道底部无液氮.当氮气质量流量为20 g/s时,排空时间为17 s;当氮气质量流量为30 g/s时,排空时间为12 s.针对不同氮气质量流量的模拟计算结果如图6所示.由图可见,随着质量流量的增大,排空时间逐渐减少.此外曲线表明,氮气质量流量与排空时间近似呈反比关系,表明排空管内液氮需要的氮气量存在一定的范围.因此在已知气源质量流量时,可预测出排空所需的时间.由于氮气流量较小时排空过程中管道底部存有液氮,需要继续通入氮气使其从进口到达出口的时间和液氮排空时间存在较大的时间差.随着氮气质量流量的增大,管道底部液氮量逐渐减少,使时间差不断缩小,最终2个时间近似相等.

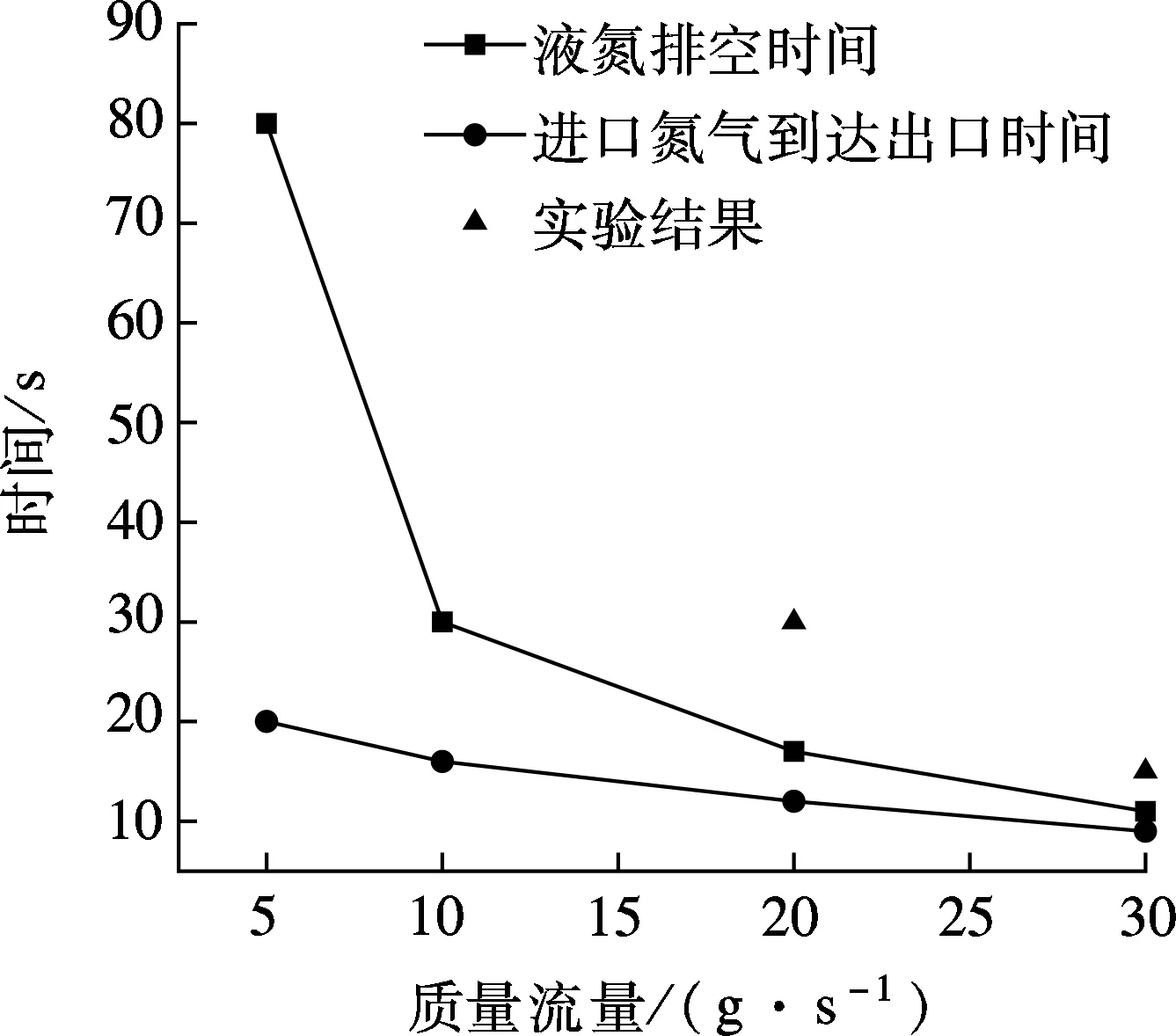
图6 氮气质量流量与排空时间关系

4.3 模拟计算结果与实验结果对比

实验选取了氮气质量流量为20和30 g/s时的2种工况,实际管路的直径、进出口高度以及管长如图1所示.同时在实际管道底部水平管道末端设有手动阀门,在认为排空过程结束后,可以通过打开阀门观察是否有残液流,来确定实验结果.模拟结果与实验结果的对比如图6所示.对氮气进气量为30 g/s的实验现象进行观察,记录液氮出口持续出液时间平均约为14～15 s. 15 s后出口无液体排出,出口为氮气. 紧接着打开底部阀门,此时无液氮流出,可认为排空过程完成. 当氮气进气量调整为20 g/s时,通过观察得到30 s后出口无液氮流出.此时打开底部阀门,仍有少量的液氮流出.同时通过图3(f)可以注意到底部水平管段在排空过程中也有少量的液氮,表明实验与CFD模拟计算得到的排空现象类似,但两者排空时间误差较大.在氮气进气量为30 g/s的情况下,实验与CFD模拟计算结果的误差为3 s左右,可近似认为模拟结果可行.但当氮气进气量为20 g/s时,虽然排空过程现象类似,但两者排空时间之间的误差较大.出现误差的原因可能是由于控制相变强度因子c的选取存在一定偏差;此外模拟计算将管道简化为绝热管道,状态不发生变化,而实际管道与外界以及管内流体会发生热交换,并受一些其他实际因素的影响.

5 结论

1) 当氮气质量流量较小,进口通入氮气虽然在很短时间内到达出口,但管道底部仍存有液氮,有明显的气液分层现象,需要继续通入氮气带来热量使液氮气化从而排空管道,增加了排空时间.当氮气质量流量较大时,在一定的时间内氮气可以将液氮完全排出,且底部无液氮残留,排空时间缩短.因此较大的气体质量流量有利于液氮的排空.

2) 将CFD模拟计算结果与实验观测结果进行比较.虽然两者结果之间存在一定的误差,但为理解管道内低温流体的排空提供了直观理解和指导.为进一步提高计算结果准确性,后续研究将从控制相变强度因子修正以及实际管路动态变化过程两方面展开.

References)

[1]Ichard M, Hansen O R, Middha P, et al. CFD computations of liquid hydrogen releases [J].InternationalJournalofHydrogenEnergy, 2012, 37(22): 17380-17389. DOI:10.1016/j.ijhydene.2012.05.145.

[2]van Dresar N T, Siegwarth J D, Hasan M M. Convective heat transfer coefficients for near-horizontal two-phase flow of nitrogen and hydrogen at low mass and heat flux [J].Cryogenics, 2001, 41(11/12): 805-811. DOI:10.1016/s0011-2275(01)00173-4.

[3]李祥东,汪荣顺,黄荣国,等.垂直圆管内液氮流动沸腾的理论模型及数值模拟[J].化工学报,2006,57(3):491-497.DOI:10.3321/j.issn:0438-1157.2006.03.004. Li Xiangdong, Wang Rongshun, Huang Rongguo, et al. Modelling and numerical simulation of boiling flow of liquid nitrogen in vertical tube [J].JournalofChemicalIndustryandEngineering, 2006, 57(3): 491-497. DOI:10.3321/j.issn:0438-1157.2006.03.004. (in Chinese)

[4]熊炜,汤轲,陈建业,等.液氮核态池沸腾CFD模拟和可视化实验[J].低温工程,2014(5):6-9,33. Xiong Wei, Tang Ke, Chen Jianye, et al. CFD simulations and experimental verification on nucleate pool boiling of liquid nitrogen [J].Cryogenics, 2014(5): 6-9,33. (in Chinese)

[5]陈亮,梁国柱,邓新宇,等.贮箱内低温推进剂汽化过程的CFD数值仿真[J].北京航空航天大学学报,2013,39(2):264-268. Chen Liang, Liang Guozhu, Deng Xinyu, et al. CFD numerical simulation of cryogenic propellant vaporization in tank [J].JournalofBeijingUniversityofAeronauticsandAstronautics, 2013, 39(2): 264-268.(in Chinese)

[6]ANSYS.ANSYSfluenttheoryguide[M]. Canonsburg, PA, USA: ANSYS Inc, 2013: 468-475.

[7]Lee W H.Apressureiterationschemefortwo-phaseflowmodeling[M]. Washington,USA:Hemisphere Publish, 1980: 407-427.

[8]de Schepper S C K, Heynderickx G J, Marin G B. Modeling the evaporation of a hydrocarbon feedstock in the convection section of a steam cracker [J].ComputersandChemicalEngineering, 2009, 33(1): 122-132. DOI:10.1016/j.compchemeng.2008.07.013.

[9]Alizadehdakhel A, Rahimi M, Alsairfi A A. CFD modeling of flow and heat transfer in a thermosyphon [J].InternationalCommunicationsinHeatandMassTransfer, 2010, 37(3): 312-318. DOI:10.1016/j.icheatmasstransfer.2009.09.002.

[10]Yang Z, Peng X F, Ye P. Numerical and experimental investigation of two phase flow during boiling in a coiled tube [J].InternationalJournalofHeatandMassTransfer, 2008, 51(5): 1003-1016. DOI:10.1016/j.ijheatmasstransfer.2007.05.025.

CFD simulations and analyses on emptying process of nitrogen pipeline

Chen Hong1Zou Yang2Liang Wenqing2Qian Hua2Gao Xu1

(1State Key Laboratory of Technologies in Space Cryogenic Propellants,Center for Engineering Design and Research Under the Headquarters of General Equipment, Beijing 100028, China)(2School of Energy and Environment, Southeast University, Nanjing 210096, China)

To investigate the emptying process of pipeline of cryogenic liquid, unsteady flow and volume of fluid (VOF) models in computational fluid dynamics (CFD) method were used to simulate of release process of the liquid nitrogen. Simulation results were validated by experimental results. The simulation results show that when nitrogen flow rate is lower, it can throughout the pipe for some time but some liquids remain in the pipe bottom. And the stratified phenomenon can be obtained. By using nitrogen injection to heat liquid nitrogen and make it evaporated, it can be empty totally at the end. Also the totally emptying time of liquid is longer. With the nitrogen flow rate increasing, the empty time is shorter. When nitrogen flow rate is beyond a certain level, the nitrogen can push and empty the nitrogen directly and no liquid remains. The results also provide a theoretical guidance for emptying liquid hydrogen and other dangerous cryogenic liquids.

pipeline releases; cryogenic liquid; numerical simulation; volume of fluid (VOF)

10.3969/j.issn.1001-0505.2016.06.023

2015-12-26. 作者简介: 陈虹(1966—),女,研究员;梁文清(联系人),男,博士,副研究员,hemelrijken@126.com.

航天低温推进剂技术国家重点实验室开放课题资助项目(SKLTSCP1512).

陈虹,邹阳,梁文清,等.液氮管道排空过程CFD模拟及分析[J].东南大学学报(自然科学版),2016,46(6):1246-1250.

10.3969/j.issn.1001-0505.2016.06.023.

TB611

A

1001-0505(2016)06-1246-05