基于积分组合的FBD谐波检测法

罗 鹏,张 威,高贵亮

(黑龙江科技大学 电气与控制工程学院,哈尔滨 150022)



基于积分组合的FBD谐波检测法

罗 鹏,张 威,高贵亮

(黑龙江科技大学 电气与控制工程学院,哈尔滨 150022)

常规电力滤波器谐波电流检测方法利用锁相环检测电压定向角,这样在参数设计时会非常复杂,不利于工程应用,除此之外,常规方法在滤波时还采用低通滤波器,它本身的固有延迟会造成系统实时性下降。为克服上述缺陷,在传统FBD检测方法的基础上提出一种改进方法。该方法在检测过程中采用广义积分器取代锁相环检测电压相位,采用积分均值法取代传统的低通滤波方式来滤除畸变电流中的谐波分量,与传统方法相比,提高了电流幅值和相位检测的精确性,缩短了响应时间。同时,仿真实验验证了该方法的正确性和可行性。

FBD法;积分均值;广义积分;谐波检测;无锁相环

FBD谐波检测法与目前常用的瞬时无功检测法相比,计算量显著减少,且适用于单相和三相系统[1-3]。大量研究已经证明FBD谐波检测法与瞬时无功检测法在检测结果方面具有一致性[4]。但以上传统方法的相似之处是都用到锁相环检测基波电压相位,并且使用低通滤波器滤去交流分量,这样就使得检测的实时性下降,不仅如此,当三相电压畸变严重时还会造成基波相位提取不准确,进而影响到谐波和无功的检测[5-6]。针对上述缺陷,本文提出将积分均值法和广义积分原理应用于FBD谐波检测法,省去了锁相环节和低通滤波环节,简化了传统检测方法。分别讨论了积分均值方法中积分区间的选取问题以及广义积分器不同增益下对谐波检测的影响效果,通过MATLAB仿真证明了新方法适用于三相不对称情况且具有更好的检测精度和更快的动态响应速度。

1 基于积分组合的FBD检测方法

基于积分均值与广义积分原理的谐波检测方法如图1所示。

1.1 基于广义积分器的无锁相环控制

图1 基于积分组合的FBD检测算法

对上述信号采用拉氏变换能够得出

在网侧频率有小的变动Δω时,三种信号都会发生变化,其中电网信号会变为

e′(t)=Asin[(ω+Δω)t+φ]

那么会有

图2 广义积分器谐波检测

从图2可以看出,该过程中没有锁相和低通滤波环节,这就省去了电压运算,所以在电网畸变时提高了检测精度。在广义积分器所采用的闭环系统中,增益k取值不同时会对谐波检测性能产生影响,分别取k=10和k=100分析系统检测性能。采取不同k值所得到的频率特性曲线如图3所示。

图3 k=10和k=100的幅频和相频曲线

从图3能够发现,当f=50 Hz时,无论k取10还是100,系统增益都约为0 dB,也就是说明系统对正弦频率为50 Hz的信号基本不衰减。进一步分析k=10和k=100时系统的相频特性发现,后者的效果要优于前者,检测精度会随着k的减小而增大,而响应速度则会随之变慢,因此为保证响应的快速性,需要在满足一定条件的情况下适当增加k值。

1.2 基于积分均值法的滤波方式

在基波电流的提取环节中,改进检测方法采用积分均值法来代替低通滤波,以此滤去电网畸变严重时的谐波分量。设T是工频周期,id、iq为dq变换后的有功与无功分量,那么电流可表示为

经傅里叶级数展开后得

将有功电流与无功电流的交流部分都按其正余弦的方式展开,展开后个各谐波在各个周期内的积分均值都为零,即

积分区间可根据实际情况设定,因为在实际中多用三相整流器,谐波电流次数多为6k+1次,依次为5、7、11次等。经过变换后负序谐波会增加一次,正序谐波会减少一次,这样可得到谐波变化的规律,进而设置积分区间是基波周期的1/6。积分后可得到与基波分量对应的直流分量,应当注意的是相应区间的调整应参照实际应用中的谐波电流次数。

2 仿真分析

为了验证积分均值法的滤波效果,将它与传统方法采用的二阶低通滤波器进行对比,用三相桥式整流电路作为谐波源,相电压为220 V,频率f=50 Hz,R=8 Ω,L=2mH,并在经过0.1 s后,电路参数变为R=4 Ω,L=1 mH。将畸变电流经dq变换后所得出的有功部分分别通过本文设计的积分均值模块与低通滤波器模块进行比较,得到的滤波效果如图4所示。

由图4可知,将有功电流分别流经两种方法设计的滤波器的电流波形后,在三相电流对称时,积分均值法在三相对称电流稳态情况下能较快滤除交流谐波分量,而在电流发生突变时也可以在较快时间内跟上电流的变化(约1/6个周期),而低通滤波则需要花费大约一个周期的时间,经过比较可知积分均值法滤波动态响应更快。

图4 积分均值法与LPF滤波性能图

为了对改进方法检测的实时性和准确性进行验证,用MATLAB软件进行了仿真。考虑到实际应用中,在负载变化的情况下,电网电压幅值会产生波动,波动范围一般在10%以下,在设置参数时,分别设置三相电压为uA=129∠0°,uB=148∠-120°,uC=148∠120°,负载电阻R=8 Ω,负载电感L=1 mH。分别利用ip-iq法、传统FBD方法以及改进FBD检测方法检测出的基波电流如图5所示。

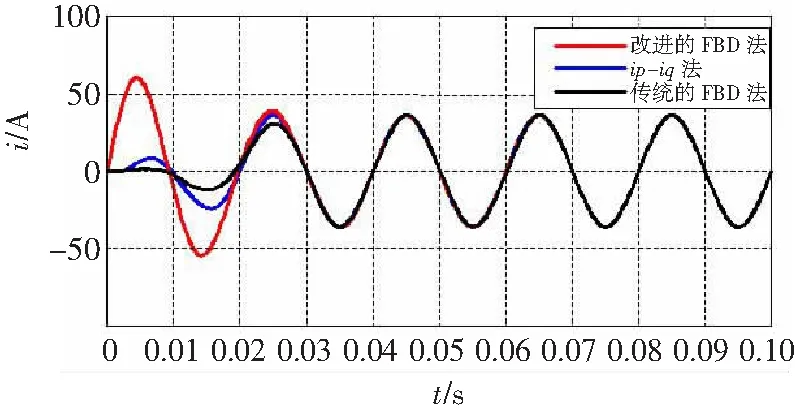
图5 三种方法下检测出的基波电流

从图5中能够看出,在给定电路参数相同的情况下,相对于常规的ip-iq法和传统FBD检测法,改进后的FBD检测方法能够更加迅速地跟上电流的变化,具有更快的响应速度,并且在电路达到稳定状态时,三种方法在最终结果上一致。

为进一步对基于积分组合的改进FBD方法的检测精度进行验证,给出了三种检测方法下基波电流的FFT分析。负载电流FFT分析如图6所示,常规FBD检测方法下基波电流t=0.02 s～0.04 s的FFT分析如图7所示,改进FBD检测方法检测的基波电流在t=0.02 s～0.04 s的FFT分析如图8所示。

图6 负载电流FFT分析

图7 常规FBD检测方法下基波电流t=0.02 s～0.04 s的FFT分析

图8 改进FBD检测方法下基波电流t=0.02 s～0.04 s的FFT分析

从图6可知,在t=0.02 s～0.04 s内对A相电流进行频谱分析之后发现电路主要存在6k±1次谐波,k=1,2,3,…,电流的基波分量有效值为32.55 A,谐波畸变率为28.76%。

从图7可知,采用传统的FBD检测方法在第二个周期(t=0.02 s～0.04 s)所检测到电流的畸变率是2.55%,而在之后的检测中发现畸变率逐渐降低,最终在第四个周期内稳定为0.33%,从中分析出传统方法在t=0.02 s～0.04 s时未达到稳态。

从图8可知,采用积分组合的改进方法在t=0.02 s～0.04 s时电流畸变率是0.12%,经过对比可以发现改进方法不仅响应速度快,而且在检测精度上也要优于传统方法。

3 结 语

本文提出了一种基于积分组合的FBD改进方法,该方法用广义积分器对基波电压正序分量进行提取,省去了锁相环,简化了传统FBD检测算法;用积分均值法取代传统的低通滤波方式,提高了响应速率。同时,仿真结果也证明了该改进算法能用于三相电压不对称时的谐波和无功检测,与传统方法相比实时性更好,精度更高。

[1] 王兆安,杨君,刘进军,等.谐波抑制和无功功率补偿[M].北京:机械工业出版社,1998.WANG ZHaoan, YANG Jun, LIU Jinjun, et al.Harmonic suppression and reactive power compensation [M].Beijing:China Machine Press, 1998.

[2] 陈峻岭,姜新建,孙卓,等.基于FBD法的三相电力系统电流检测方法的应用[J].电力系统自动化,2004,28(24):23-27.CHEN Junling, JIANG Xinjian, SHUN Zhuo,et al.Current detections for three-phase power system based on FBD method[J].Automation of Electric Power Systems,2004,28(24):23-27.[3] 王小红.基于瞬时无功功率理论的并联混合有源电力滤波器的研究[D].天津:天津大学,2005.WANG Xiaohong.Research on the parallel hybrid active power filter based on the instantaneous reactive power theory[D].Tianjin:Tianjin University,2005.

[4] 刘心旸,王杰.基于瞬时无功功率理论的自整定因子变步长低通滤波器研究[J].电力系统保护与控制,2012,40(10):84-89.LIU Xinyang,WANG Jie.A variable step-size low-pass filter with self-tuning factor based on instantaneous reactive power theory[J].Power System Protection and Control,2012,40(10):84-89.

[5] 于晶荣,曹一家,关维德,等.基于FBD法的有源电力滤波器参考电流检测新方法[J].湖南大学学报(自然科学版),2011,38(2):45-50.YU Jingrong, CAO Yijia, GUAN Weide,et al.A new reference current detecting algorithm based on FBD method for active power filter[J].Journal of Hunan University(Natural Sciences),2011,38(2):45-50.

[6] 时国平,许卫兵,王长春.基于FBD法的三相四桥臂 APF的研究[J].自动化与仪器仪表,2010,28(5):22-24.SHI Guoping, XU Weibing, WANG Changcun.Study based on three-phase four-leg APF of FBD method[J].Automation &Instrumentation,2010,28(5):22-24.

[7] 王杰,申张亮.基于FBD谐波检测方法的有源电力滤波器系统设计[J].电工电气,2010(8):9-13.WANG Jie,SHEN Zhangliang.Design of active power filter system based FBD harmonic detection method[J].Electrotechnics Electric,2010(8):9-13.

[8] 吴峰,郑建勇,梅军.谐波电流检测技术的理论与FBD法仿真试验研究[J].低压电器,2011(15):45-50.WU Feng, ZHENG Jianyong,MEI Jun.Research of simulation and experiment for theory of harmonic detecting method and FBD method[J].Low Voltage Apparatus,2011(15):45-50.

(责任编辑 侯世春)

FBD harmonic detection method based on integral combination

LUO Peng, ZHANG Wei, GAO Guiliang

(School of Electrical &Control Engineering, Heilongjiang University of Science &Technology, Harbin 150022, China)

The conventional method uses phase-locked loop to detect the voltage orientation angle, by which the parameters are very complicated to design, leading to bad effects in engineering applications.Besides, the low pass filter adopted, which has an inherent delay lowering the real-time while filtering.In order to overcome the above shortcomings, this paper proposed the improved method on the basis of the traditional FBD method.It is a method that replaces the phase-locked loop by the generalized integrator to detect voltage phase, and the traditional low pass filter by the integral average method to remove distortion harmonic and to extract the DC component.Compared with the traditional method, the improved method makes the detection of the current amplitude and phase more accurate with the shortened response time.The simulation results verify the correctness and feasibility of the improved method.

FBD method;integral average;generalized integral;harmonic detection;non phase-locked loop

2016-04-24。

罗 鹏(1992—),男,硕士研究生,研究方向为电力系统及其自动化。

TM935

A

2095-6843(2016)05-0439-04