高渗透率下分布式决策的负荷预测模型

郭国栋

(天津科技大学,天津 300222)



高渗透率下分布式决策的负荷预测模型

郭国栋

(天津科技大学,天津 300222)

为提高分布式新能源在电网中的渗透率和寻找有效的负荷预测方法,提出一种基于动态贝叶斯网络的分布式决策模型,对电网负荷进行精确预测,即先用分类器按照负荷性质将大电网进行聚类划分,通过考虑影响负荷的各类因素以及这些因素之间的关系,对各个分布式网络进行动态贝叶斯网络建模,然后用贝叶斯优化的方法以及转移网络对模型进行优化,再用决策网络对其进行总体预测。最后,通过实际算例计算、分析结果表明,这种方法在渗透率小的一般预测时,具有较高的精度,且学习时间短,适合在线预测。

动态贝叶斯;分布式;负荷预测;决策网络;渗透率

智能电网是新型现代化电网,可以最大限度接纳清洁能源,实现低碳绿色生活,提高电网安全稳定性[1]。在这个框架下,随着大规模可再生能源的并网,其对电网的渗透率不断提高,分布式电源输出功率的波动也会在电网系统的安全性与经济性上产生重大影响[2]。精准的电力负荷预测可以有效保障电力系统的安全,并且经济合理地安排电力发电系统的启停[3],最大程度地利用可再生能源[4-5]。

传统的负荷预测算法包括SVM预测算法[6]、神经网络算法[7]、灰色模型预测方法[8]。SVM算法对大规模训练样本难以实施且存在分类问题,神经网络算法收敛速度慢且容易失败,灰色模型误差偏大。然而贝叶斯网络(Bayesian network, BN)为分布式电网负荷预测提供了一种可行的方法。BN理论是采用概率理论在网络节点上进行概率推理,可以由一些已知节点的概率推算出另外一些节点的概率。动态贝叶斯网络(dynamic Bayesian network, DBN)在普通的贝叶斯网络基础上加入了时间信息,把原来的静态贝叶斯网络与时间信息结合,形成具有处理时序数据的随机模型。在分布式新能源发电负荷并网的电力系统中,风能发电的功率与某一时刻的风速、风向有关,光伏发电的输出功率与太阳辐射度、环境因素有关,而一般情况下的负荷预测与天气因素(最高温度、最低温度、降雨量等)和可中断负荷因素有关。这些因素都是随机的,且同一时刻不同因素之间与不同时刻同一因素之间是相互影响的。基于此,本文根据电网中电源性质的相近性利用构造贝叶斯网络分类器的方法对整个电力系统网络进行划分,分析影响每个小网络负荷因素之间的关系,构造动态贝叶斯预测模型,然后探讨电网总负荷与各个子电网负荷之间的关系,从而对整个电力网络进行精准预测,最后通过算例计算、分析结果验证其正确性。

1 电力网络的划分

1.1 根据负荷性质划分

因为分布式电源的渗透率不断提高[9-11],对电网来说是一个不可控源,所以在实际应用中将分布式电源结合在微网中去。微网一般通过单点接入电网,在电网端被视作可控发电源或负荷,微网可以并入电网或在孤岛模式下运行,同一微网地理位置相近,条件也比较相似,往往可以根据性质[12]划分为一类电网。在电网中,商业用电、居民用电、工厂用电是不同性质的用电,体现为不同的负荷特性,因此在电网划分中也可以划分为几块电网。

1.2 Multi Agent技术的借鉴

划分好的电网与上级电网之间是一个分散式的控制(如微网与上级电网之间),Multi Agent技术是将一个大的系统划分为几个小的系统,整个系统的预测任务可以由几个小的系统相互协作完成,并具有以下几个方面的优势:

1) 多代理技术符合电力系统分布化的趋势,能够达到分布电源精确预测的目的。

2) 除了预测之外,这种划分方式的应用有利于上级电网与下级电网以及下级电网之间的协调控制。

3) 通过这种划分可以找到影响负荷的主要因素,有利于制定滚动计划或调峰计划。

4) 多代理系统可以加强下级电网对上级电网的支撑,改善预测结构。借鉴多代理系统的结构,可以根据电网负荷性质的相似性构造贝叶斯网络分类器对整个电网进行划分。

1.3 贝叶斯分类器的构造

贝叶斯分类实现的核心方法是构造贝叶斯网络。其主要思想是:在给定的待分样本的条件下计算类别的后验概率,确定每个小部分的后验概率。

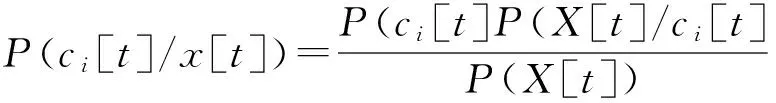
式中:X[t]={X1[t],X2[t],…,Xn[t]}为在t时刻属性变量的集合,0≤t≤T,而x[t]={x1[t],x2[t],…,xn[t]}是来描述n个属性节点X1[t],X2[t],…,Xn[t]在t时刻的n个度量,xi[t](i=1,2,…,n)表示属性Xi可能的取值；C[t]表示t时刻片段的类节点,ci[t]则表示相对应的类节点C的取值。对于类来说,P(x[t])为常数,P(Xi[t])表示类的先验概率。

考虑到时间因素,动态贝叶斯分类器是由许多时间片段构成的。在时间序列下,C={C[0],C[1],…,C[T]}为类变量序列,X={X[0],X[1],…,X[T]}则是属性变量序列,其中X[t]={X1[t],X2[t],…,Xn[t]},此时0≤t≤T。动态贝叶斯分类器的结构如图1所示。

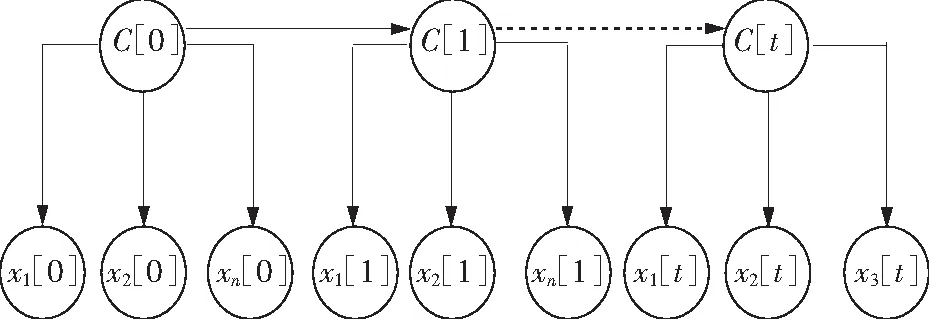
图1 动态贝叶斯分类器结构

通过网络分类,将各类信息归类到各个数据库,对结构进行分析,调整划分方向。

2 动态贝叶斯网络的分布式模型

2.1 动态贝叶斯预测网络的构造

通过将较大的电网进行划分,可以得到多个较小的网络。因为小网络性质相似,所以对负荷预测更为方便,结果也更为精确。各个分布式网络的预测遵循相似的原则。

首先,为了能对负荷进行准确预测,这个网络应包含对分布式负荷起重要作用的关键因素[13]。

F(v)=1-e-(v/λ)k

Prob(0)=F(v1)+[1-F(v3)]= 1-e-(v1/λ)k+e-(v3/λ)k

Prob(Pw)=F(v3)-F(v2)= e-(v2/λ)k-e-(v3/λ)k

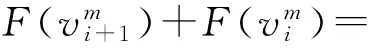
式中:v为风速,λ为尺度参数,k为形状参数,Vim为区间[V1,V2]经过离散化之后的第i段风速,F(v)为风速的累积分布函数,Prob(0)为当风机的有功功率为零时的概率,Prob(Pw)为风机的有功功率为Pw时的概率,Prob(Pi+Pi+1)/2为风机在第i段内为(Pi+Pi+1)/2时的概率。

对于光伏来说,其负荷与光照强度G和组件温度T有关,而组件温度又与光照强度和环境温度有关,有如下关系:

T=Ta+kG

式中:Ta为环境温度,k为相关系数。

上述各种因素之间在同一时刻是相互影响的,相同的因素在相邻时刻也是相互影响的,同一因素在时间序列下具有一定的自相关性。

这里先选定风速V、光照强度G、组件温度T、环境温度以及负荷功率P,其他因素可以用同样的方式加入到网络中。

因为某一时刻负荷功率受到这一时刻风速、光照强度、组件温度和环境温度的影响,同时在时序上也与上一时刻的负荷功率有着紧密联系,因此有如下因果关系:

P(Pt+1|Pt,Vt+1,Gt+1,Tt+1)

式中:P为负荷功率,下标t和t+1分别表示当前时刻和预测时刻。

组件温度、光照强度和环境温度有如下因果关系:

P(Tt+1|Gt+1,Tat+1)

再考虑时序上的关联性,风速、组件温度、环境温度和光照强度还有如下因果关系:

P(Vt+1|Vt)，P(Tt+1|Tt)，

P(Tat+1|Tat)，P(Gt+1|Gt)

上述因果关系可以用局部贝叶斯网络表示,如图2所示。

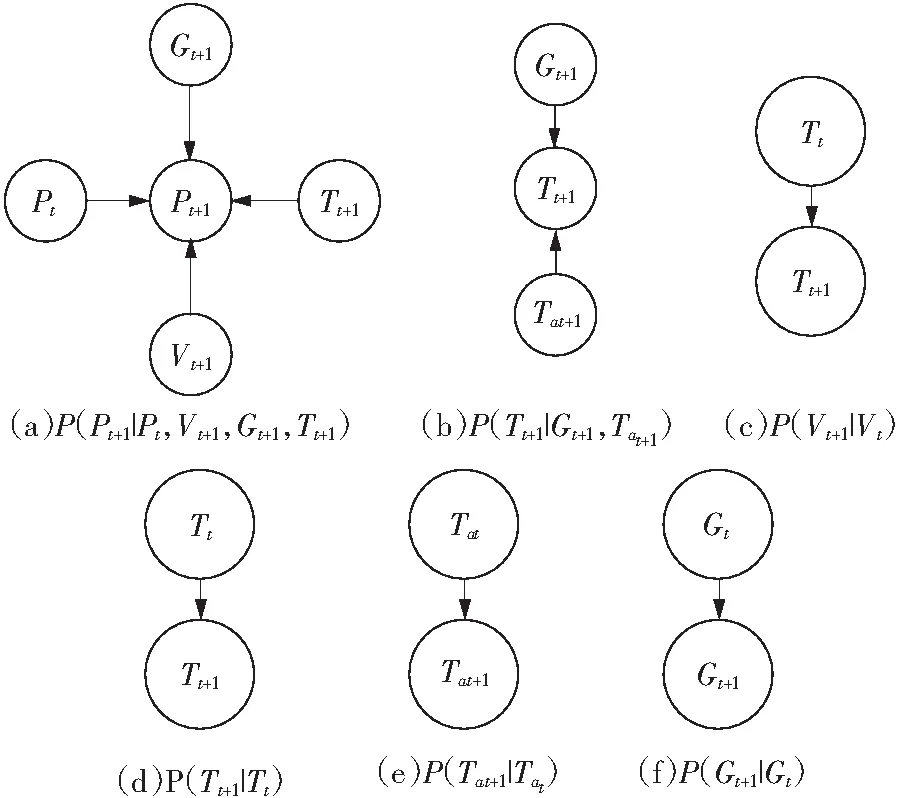
图2 局部贝叶斯网络图

将以上网络进行组合,得到静态贝叶斯网络,如图3所示。

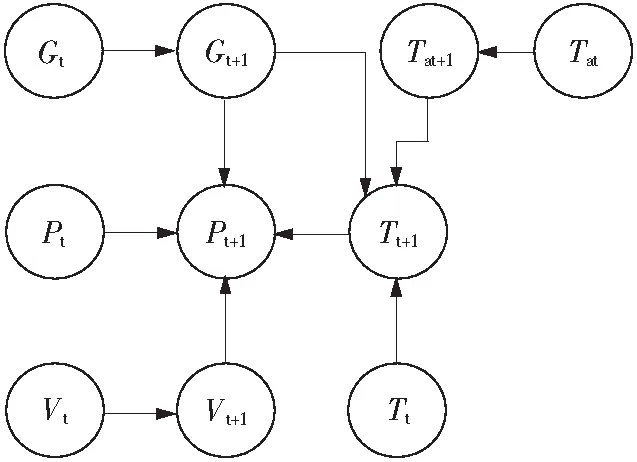
图3 静态贝叶斯网络图

再结合时间序列信息,可以得到动态贝叶斯网络,如图4所示。

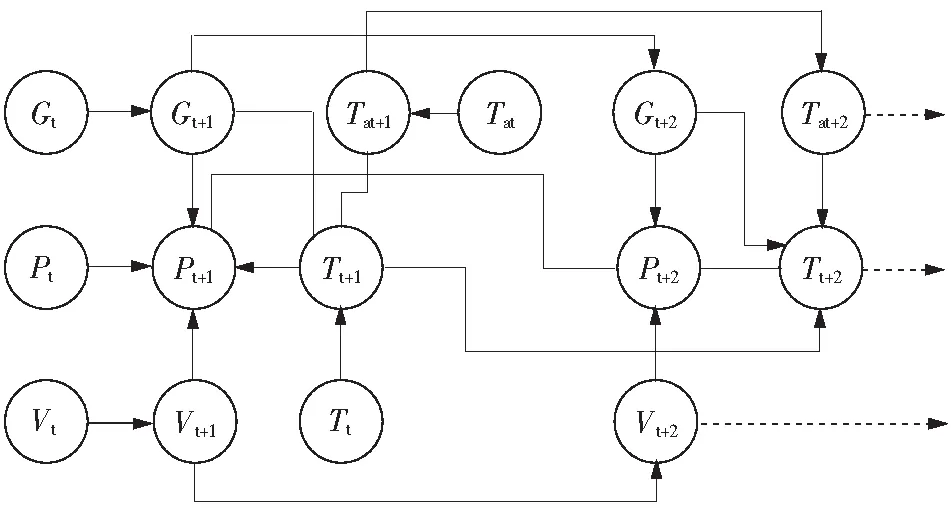
图4 动态贝叶斯网络图

这样,动态贝叶斯网络就形成了。

2.2 动态贝叶斯网络参数节点的计算

当数据比较完备时,根据EM[14]算法,可以算出参数的极大似然估计,完成参数一个周期的更新。似然函数为L(θ:D),X={X1,X2,…,Xn}为动态贝叶斯网络的变量集,Xi[m]是节点在第m个样本中的数据,Pai[m]是父节点集的配置,θ是待估参数,D是样本集。则公式为

L(θ:D)=∏mP(X1[m],…，Xn[m]:θ)= ∏m∏iP(Xi[m]|Pai[m]:θi)= ∏i∏mP(Xi[m]|Pai[m]:θi)= ∏iLi(θi:D)

似然函数就被分解成为n个独立的参数极大似然估计问题。令N(Xi,Pi)为变量的充分统计因子,可以得到

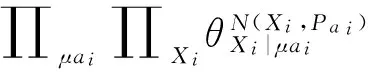
θXi|μai的最大似然估计为

(1)

2.3 动态贝叶斯网络的优化

为了能使网络在负荷预测中实时地解决问题,实现在线预测,本文提出了贝叶斯优化(Bayesian Optimization Algorithm, BOA)与动态贝叶斯(DBN)网络结合的算法。

在网络图形模型智能优化的基础上,将DBN网络作为转移网络,在整个动态优化的过程中,转移网络的作用非常重要。当样本信息在时序轴上的t到t+1轮优化条件变化时,转移网络会感知到所处环境的变化,基于对当前状态的理解从而进行实时负荷预测。其过程如图5所示。

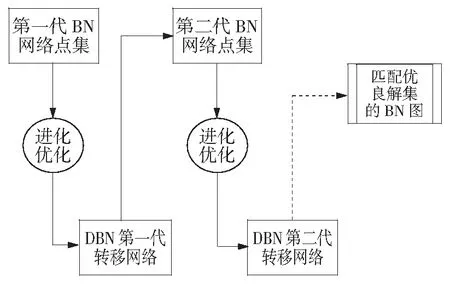
图5 BOA与DBN的混合优化机制

DBN网络感知到网络节点集合发生变化后,适时改变基本条件,重新确立了新的种群以及优化方向,大大提高了负荷智能预测的自主能力。

为了简化计算,一般往往可以去掉网络一些不重要的节点,继承上一代转移网络的优点,重新计量一些边。这样就需要进行网络搜索,而一般的搜索算法往往要搜索大量的节点空间,为了提高运算速度,采用一种启发式算法。

首先将时间T分成n个时间段,每个时间段长度为Δt=T/n，将每段进行计算再综合。设定评分函数为

(2)

从0时刻起的Δt时间内,测得一批动态数据D1,基于前面的BOA方法,从所有的DBN结构中搜索到的第一个最高评分SCORE1对应网络DBN1,再经过一个Δt,得到SCORE2和DBN2,最后在nΔt即T时间内得到SCORE0:T对应的DBN0:T。这里所进行的综合指的是以网络结构出现的概率为基础,考虑有向边出现的次数。

3 决策网络的总体预测

3.1 BN决策网络的构建

前面已经将一个大电网进行划分,又对各个划分的电网进行了分布式负荷预测。除了考虑各个分布式电网外,还得结合上级电网和用户测的数据,从而对整个电网进行一个预测,决策网络的工作机制如图6所示。

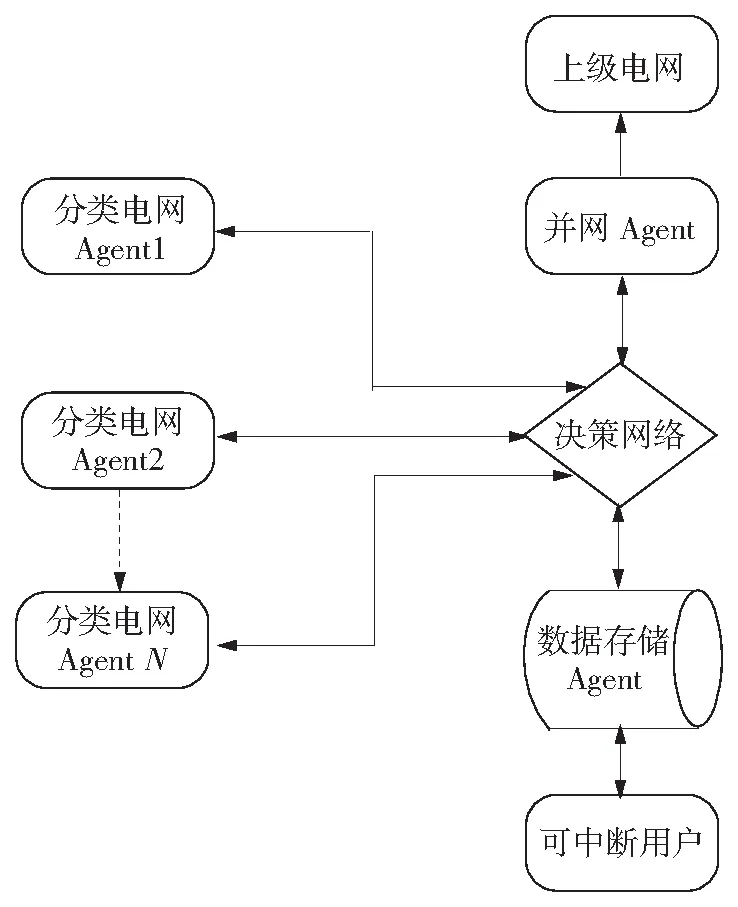
图6 决策网络的工作机制

为了精确、简洁、快速地对大电网进行总体的预测,这里构造一个决策网络。

由于分布式网络通过感知环境后所形成的网络节点集合的空间是很庞大的,实际应用中需要在较短的时间内找到决策网络的结构,而以往的遗传算法和进化算法并不具有处理这种结构的效率性,因此可以采用改进进化算法的快速BN构图法进行寻找。

设所有变量的集合I={X1,X2,…,Xn},其基本流程如下:

1) 选择初始节点Xroot,其原则是使变量取值分别为0和1时所对应的染色体个数相差的绝对值最大。

2)Iin表示之前已经生成的部分树形模型中的变量集,Iout=I-Iin。对于集合中的Xi∈In和Xj∈Iout,搜索到最大的BD(Xin-i→Xout-j),也就是寻找:

BD(Xin-i→Xout-j)=max{BD(Xi→Xj)|Xi∈Iin,Xj∈Iout}。

3) 把节点Xout-j加入Iin中去,使之成为Xin-i的子节点,这样局部就增长了一个树叶,于是

Iin←Iin∪{Xout},Iout←Iout∪{Xout-j}

4) 返回2),当集合I与Iin相等时结束。

用上述过程构造决策网络时,为了进一步简化运算,应按照以下原则进行:节点的独立性越弱越先添加一个边指向它,一对节点相似性越强越先连接它们的边,不同节点连接边的添加具有可加性,而同一节点连接边的添加并不具有可加性。

在整个动态时序过程中,某一时刻的预测方向和优化点的集合都可以遗传给下一代的BN决策网络做负荷预测使用。

3.2 BN决策网络预测的优点

BN决策网络的构造及前文转移网络共同组成了整个模型的双核心结构。

将大电网进行划分,再用动态贝叶斯网络进行学习和预测,大大提高了预测的鲁棒性和精确性。BN决策网络的使用使算法有了较快的收敛速度,能够实现实时自主控制,即高度智能化。

BN决策网络不仅考虑了每个分布式电网,还将客户端与上级电网考虑了进来。此外,它还具有良好的扩展性,体现在以下几个方面:

1) 当决策网络与专家系统结合时,受益于决策网络的高度智能化,将会大幅度提高电网的运行效率。

2)将决策网络的优化方向进行改变,则可以将其功能扩展到负荷预测之外的广阔领域。如果将其优化方向改为改善不间断供电,那么结合新能源发电技术和新型储能技术,可以使功率输出平滑,提高其稳定性。此外,在故障检测和用户交互方面也有天然的优势。

4 算例分析

为验证本文提出的负荷预测模型,使用Matlab中的FULLBNT工具箱进行网络构建。

以某地区夏季的日负荷数据为研究对象,数据采集时间间隔为60 min。选取天气因素相似的2013年5月31日—2013年5月20日的电力数据和气候数据进行计算,来预测5月21日0—24时的负荷，其中3个捕捉到的时间点的数据如表1所示。

表1 三个时间点的历史数据

按照负荷性质对样本进行划分。为了了解负荷的时间性质和空间性质,在matlab环境下做出相对负荷在时间维度与空间维度的三维仿真图,这里先将样本进行归一化处理。将负荷处理到[0,1]区间内,时间维度本身就已限制在[0,24]区间内,无需再进行处理。在空间位置上选取几何中心点,由远及近将空间维度处理在[0,10]区间内。归一化公式为

将所有数据进行处理,得到负荷的三维特性如图7所示。

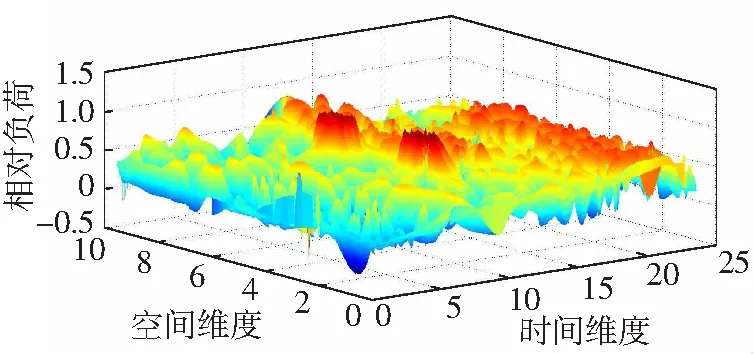
图7 负荷的三维特性

从图7可以看出,颜色的深浅代表相对负荷的大小,在时间维度10到11,空间维度4和7的位置有2个高峰,而在时间维度20到22时,在整个空间上延绵一片小高峰,在时间维度0到4时又出现成片蓝色低谷,在空间上也有较好的集中性。为了给贝叶斯处理提供条件,这里采用非负矩阵分解法将其进行降维处理,如图8所示。

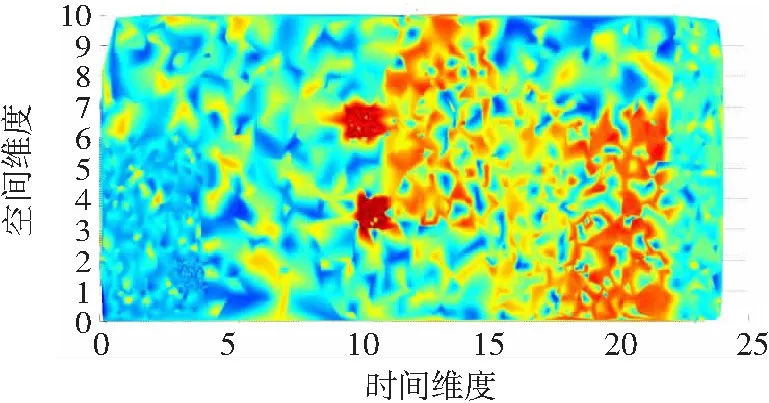
图8 负荷特性的降维分类

可以利用贝叶斯分类器来处理这个二维图像减少计算量。再利用式(2)计算各分类网络在各个时间段内的评分。

分析各个分布式网络与风速、温度、湿度关系的强弱,找到强属性集G1和弱属性集G2。强属性集G1={A1,A2},弱属性集G2={A3},在要求计算速度的前提下可以忽略A3,如表2所示。

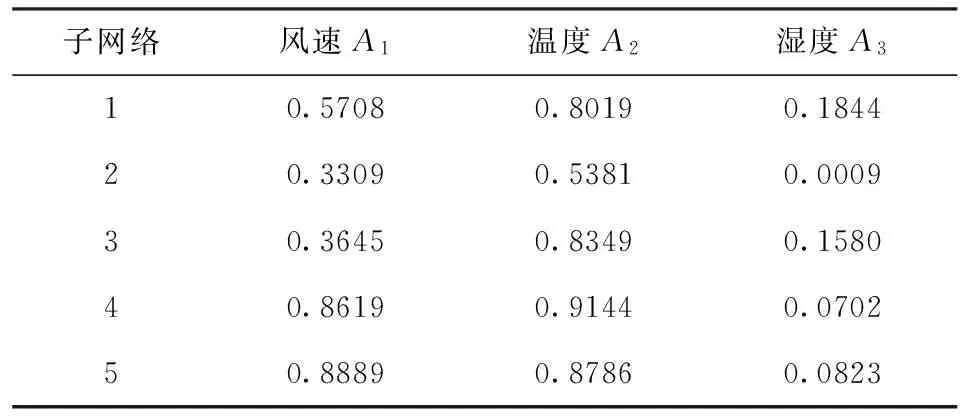
表2 影响因素的关联性结果

在对分类后的每一部分电网中,利用本文所提出转移矩阵的方法,以式(1)作为目标函数,利用分布式协同进化算法将其在动态贝叶斯决策网络中进行迭代。

决策网络中,为寻找BD(Xin-i→Xout-j)=max{BD(Xi→Xi)|Xi∈Iin,Xi∈Iout},将风速、湿度、温度的值处理为网络点之间的概率值,经过多次学习得到最优参数,如图9所示。

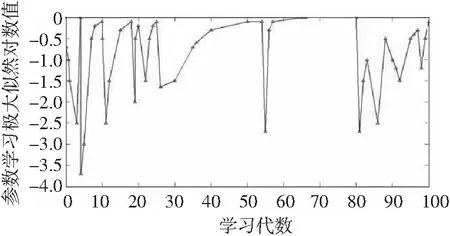
图9 决策网络参数学习曲线

在图9中,实际运行65代就已能得到最优解和最优参数,当前后代数参数学习极大似然值的差小于0.001时就终止迭代了,但因为在线运行时继续调整参数,故65代后还在继续。

通过动态贝叶斯方法可以得到各个时刻的状态区间,即各负荷出现在某一个值上的概率。本文采取某一时刻概率最大值所对应负荷区间的中位数作为这一时刻的预测值。如5月21日8时的状态区间,如图10所示。这一刻的预测值就为270 MW。

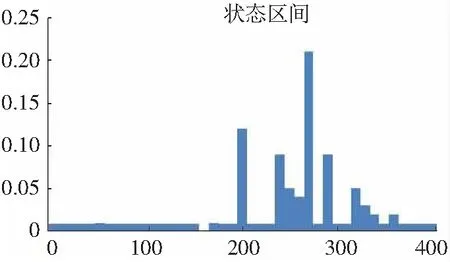
图10 负荷预测的概率分布

将本文的算法与一般的灰色神经算法的预测结果进行对比,如图11所示。

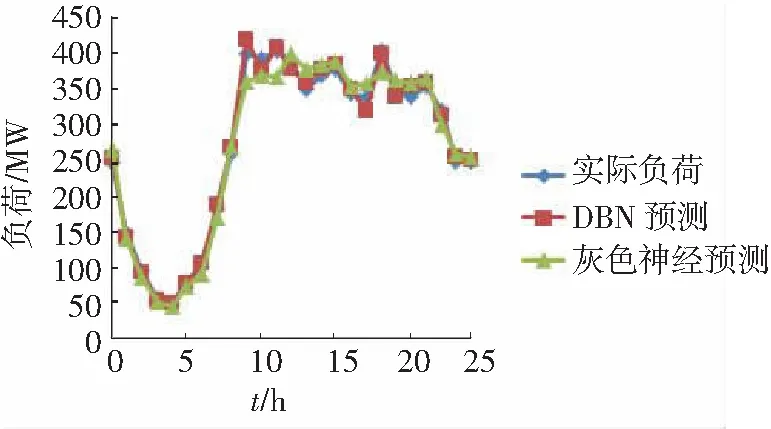
图11 负荷预测对比图

从图11可以看到,本文所提出的模型可以有效地跟上实际负荷的变化,而灰色神经预测模型在中间段有明显的滞后性。

采取均方根误差作为判断负荷预测结果准确性的指标,负荷预测的均方根误差曲线如图12所示。

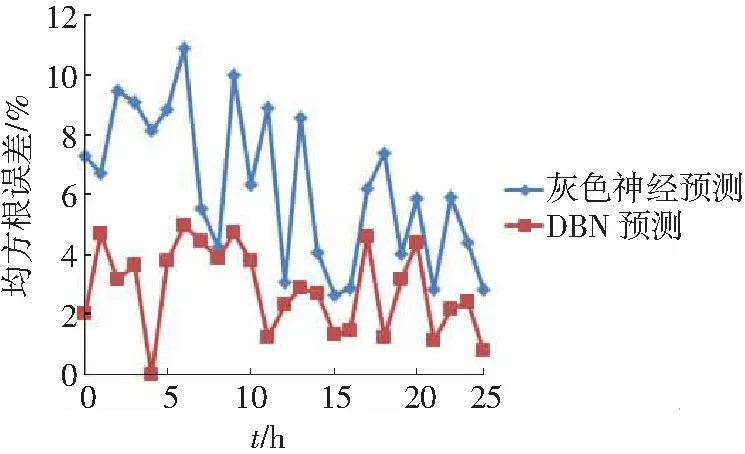
图12 负荷预测的均方根误差曲线

因为实际选址条件限制,本例中分布式能源的渗透率并不高,但通过图9可以看出,DBN预测的结果还是较为精确的,误差可控制在5%以内,符合负荷预测的误差标准,证明基于DBN的分布式决策网络预测方法是可行的。而灰色预测方法较为粗糙,误差达到了10%。由此可见,在一般负荷预测中,本文所述方法也是适用的。当新能源的渗透率更高时,本文方法的优越性将会更加明显。为了分析本文模型是否适用于在线预测,本文采用整个学习过程的收敛时间作为判断指标。普通动态贝叶斯网络与分布式决策贝叶斯网络计算性能的对比如图13所示。

从图13可以看到,当样本数据较小时,两者的差别并不大,但随着数据量的增大,预测所需的学习时间有了明显的不同,这说明分布式决策比贝叶斯更适合在线预测。

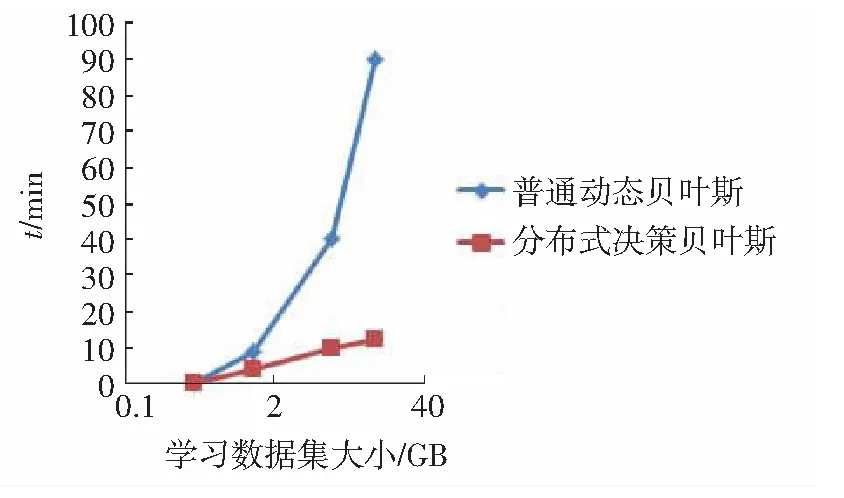
图13 算法所需时间对比

5 结 论

1) 利用动态贝叶斯网络方法,考虑时序因素,充分利用历史大数据进行学习,能提高预测精度。

2) 按照负荷性质,通过分类器对大电网进行聚类划分,并进行分布式计算,能有效降低了网络的复杂度。

3) 提出了决策网络方法,结合分布式网络,可大大降低计算复杂度。而且决策网络扩展性好,可以用于电网优化、故障检测等方面。

4) 这种方法在渗透率较小的一般预测时,具有较高的精度,且学习时间短,适合在线预测。

[1] 张东霞, 姚良忠, 马文媛.中外智能电网发展战略[J].中国电机工程学报, 2013, 33(31):1-14.ZHANG Dongxia, YAO Liangzhong, MA Wenyuan.Development strategies of smart grid in China and abroad[J].Proceedings of the CSEE, 2013, 33(31):1-14.

[2] 鲍薇, 胡学浩, 何国庆, 等.分布式电源并网标准研究[J].电网技术, 2012, 36(11):46-52.BAO Wei, HU Xuehao, HE Guoqing, et al.Study on standard for grid-integration of distributed resources[J].Power System Technology, 2012, 36(11):46-52.

[3] 黄海涛, 胡学英, 李翔, 等.实用化的激励性可中断负荷最优补偿定价模型[J].电网技术, 2014, 38(8):2149-2154.HUANG Haitao, HU Xueying, LI Xiang, et al.A practicable optimal compensation pricing model for incentive interruptible load contract[J].Power System Technology, 2014, 38(8):2149-2154.

[4] 王继业, 季知祥, 史梦洁, 等.智能配用电大数据需求分析与应用研究[J].中国电机工程学报, 2015, 35(8):1829-1836. WANG Jiye, JI Zhixiang, SHI Mengjie, et al.Scenario analysis and application research on big data in smart power distribution and consumption systems[J].Proceedings of the CSEE, 2015, 35(8):1829-1836.

[5] 张东霞, 苗新, 刘丽平, 等.智能电网大数据技术发展研究[J].中国电机工程学报, 2015, 35(1):2-12.ZHANG Dongxia, MIAO Xin, LIU Liping, et al.Research on development strategy for smart grid big data[J].Proceedings of the CSEE, 2015, 35(1):2-12.

[6] 胡时雨, 罗滇生, 阳霜, 等.基于多变量 LS-SVM 和模糊循环推理系统的负荷预测[J].计算机应用, 2015, 35(2):595-600. HU Shiyu, LUO Diansheng, YANG Shuang, et al.Load forecasting based on multi-variable LS-SVM and fuzzy recursive inference system[J].Journal of Computer Applications, 2015, 35(2):595-600.

[7] 庞清乐.基于粗糙集理论的神经网络预测算法及其在短期负荷预测中的应用[J].电网技术, 2010, 34(12):168-173.PANG Qingle.A rough set-based neural network load forecasting algorithm and its application in short-term load forecasting[J].Power System Technology, 2010, 34(12):168-173.

[8] 葛少云, 贾鸥莎, 刘洪.基于遗传灰色神经网络模型的实时电价条件下短期电力负荷预测[J].电网技术, 2012, 36(1):224-229.GE Shaoyun, JIA Ousha, LIU Hong.A gray neural network model improved by genetic algorithm for short-Term load forecasting in price-sensitive environment[J].Power System Technology, 2012, 36(1):224-229.

[9] 王深哲, 高山, 李海峰, 等.含高渗透率间歇性电源的电网规划方案优选方法[J].电网技术, 2013, 37(8):2129-2135.WANG Shenzhe, GAO Shan, LI Haifeng, et al.Optimal selection of planning schemes for power grid with high penetration of intermittent generation[J].Power System Technology, 2013, 37(8):2129-2135.

[10] KERIN U.Dynamic security indication in power systems with large amount of renewanles[C]//Power and Energy Society General Meeting.San Diego:IEEE,2012:1-6.

[11] 施琳, 罗毅, 施念, 等.高渗透率风电—储能孤立电网控制策略[J].中国电机工程学报, 2013, 33(16):78-85.SHI Lin, LUO Yi, SHI Nian, et al.A control strategy of isolated grid with high penetration of wind and energy storage systems[J].Proceedings of the CSEE, 2013, 33(16):78-85.

[12] 田书, 王丽.考虑负荷类型的含分布式电源系统对 配电网电压的影响[J].电网与清洁能源, 2014, 30(2):43-47.TIAN Shu, WANG Li.Influence of DG on the distribution network voltage considering the load type[J].Power System and Clean Energy, 2014, 30(2):43-47.

[13] 高元海, 王淳.基于全概率公式的含风电配电系统概率潮流计算[J].中国电机工程学报, 2015, 35(2):327-334.GAO Yuanhai, WANG Chun.Probabilistic load flow calculation of distribution system including wind farms based on total probability formula[J].Proceedings of the CSEE, 2015, 35(2):327-334.

[14] 俞奎, 王浩, 吴信东, 等.贝叶斯网络的并行EM学习算法[J].模式识别与人工智能, 2008, 21(5):670-675.YU Kui,WANG Hao, WU Xindong, et al.Leaning Bayesian networks using a parallel EM approach[J].PR &Al, 2008, 21(5):670-675.

(责任编辑 张兴业)

Load forecasting model based on distributed decision-making with high penetration

GUO Guodong

(Tianjin University of Science and Technology, Tianjin 300222, China)

In order to enhance the penetration rate of distributed new energy in the grid and to find the effective way to forecast load, this paper proposed the distributed decision-making model based on dynamic Bayesian network to accurately predict the load on the grid.It is a method that firstly uses the classifier to divide and cluster the large grid according to the nature of the load.Then by considering all kinds of factors that influence the load and the the relationship between these factors, it establishes the model of distributed networks by dynamic Bayesian network, optimizes the model by the optimization of Bayesian method and the transfer network, and forecasts the overall load by decision-making network.Finally, the calculation and the analysis of the example shows that this method, of which the learning time is short, is effective and accurate in the system with small penetration and, which is suitable for on-line load forecasting.

dynamic Bayesian;distributed;load forecasting;decision-making network;penetration

2016-04-12。

郭国栋(1995—),男,研究方向为电力系统及自动化。

TP393

A

2095-6843(2016)05-0432-07