改进的蒙特卡洛算法在变电站风险评估中的应用

杨杰明李兆成郭 彤

(1.东北电力大学 信息工程学院,吉林 吉林 132012;2.福建省电力工程承包公司,福州 350005)



改进的蒙特卡洛算法在变电站风险评估中的应用

杨杰明,李兆成1,郭 彤2

(1.东北电力大学 信息工程学院,吉林 吉林 132012;2.福建省电力工程承包公司,福州 350005)

针对电力系统进行风险评估时传统非序贯蒙特卡洛抽样法需要面临的抽样次数多、仿真时间长的问题,提出一种改进的蒙特卡洛算法。首先构造各个元件的零方差近似函数,求得元件的最优参数,然后结合分散抽样方法进行抽样。通过分散抽样、蒙特卡洛抽样两种方法的结合,达到提高蒙特卡洛的抽样效率、加快计算速度的目的。基于IEEE-RTS变电站部分与传统的抽样方法(分散抽样法、交叉熵重要抽样法)进行对比验证,改进方法在针对小概率事件时有较大的优势。

变电站;风险评估;蒙特卡洛;分散抽样法;重要抽样

在对变电站进行风险评估时,相对于解析法,蒙特卡洛方法能够更好地处理多重连锁故障,并且能够较快地计算出变电站的故障模式。但是为了获得较高的风险性指标,蒙特卡洛方法需要对各设备元件进行较长时间的仿真运算,对风险不能够及时处理。现在常用减小方差的方法有对偶变数法、控制变量法、分裂与轮盘赌算法、分层抽样法、重要抽样法等。文献[1]提出自适应与重要抽样法结合技术,由于系统概率特性构造确定抽样密度初值,因此在系统低风险时抽样效率退化,导致该方法计算效率降低。文献[2]是把重要抽样方法和分层抽样方法结合，通过该方法使蒙特卡洛的计算效率有所提高[3-5]。而本文提出用一种改进的算法来减少仿真时间,提高效率。

1 基本方法

1.1 蒙特卡洛法

蒙特卡洛法分为非序贯蒙特卡洛法和序贯蒙特卡洛法。本文采用非序贯蒙特卡洛法,主要步骤如下:

1) 对于由m个元件组成的系统,X=(X1,…,Xk,…,Xm)表示系统的状态变量,元件k(k=1,2,…,m)的状态变量为Xk。Xk=1时元件k处于失效状态,Xk=0时处于工作状态。不同元件的失效是相互独立的。用λk表示元件k的失效概率,状态变量Xk为

(1)

式中:ξk为区间[0,1]的随机数。系统中的各个元件状态通过式(1)确定。

2) 分析状态X,判断是否为失效状态。

3) 在获得步骤2)结果后,重新设置系统风险参数。风险性参数方差值为

式中:S为仿真状态的个数。

4) 判断方差系数是否达到一定的精度,若达到,终止计算,输出结果;反之,则返回步骤1)。用方差系数β作为反映计算精度的收敛判据:

(2)

(3)

式(3)表明,在收敛值一定的前提下,通过减小抽样随机数方差来减少抽样次数是最有效的办法[6]。

1.2 交叉熵重要抽样原理

式中:f(X;u) 为随机变量X的原始概率密度函数;u为原始概率密度函数参数;W(X;u)为似然比函数;g(X)为随机变量X的可变密度函数。

m的无偏估计为

可采用基于交叉熵的方法来近似构造g*(X),即在概率密度函数分布f(X;u)的分布簇f{f(.;v)}(v为引用参数)中,通过确定参数v,选择与g*(X)的Kullback-Leibler距离最近的密度函数{f(.;v)}作为g*(X)的近似函数,Kullback-Leibler距离即为交叉熵。g*(X)与{f(.;v)}之间的Kullback-Leibler距离(交叉熵)表达式为

D(g*(X),f(X;v))=∫g*(X)lng*(X)dX- ∫g*(X)lnf(X;v)dX

(4)

然后通过交叉熵的的方法对式(4)进一步处理得到最终的式子:

(5)

以f(X;w)(f(X;u)∈f(.;v))作为度量变化,式(5)再用一次重要抽样方法,最终得到:

(6)

式中:W(X;u;w)为似然比函数;Ew为概率密度函数f(X;w)的期望。

通过对式(6)的求解获得最优参数v*,进一步得到密度函数f(.;v*)。

由上分析,可以看到测试函数F的值大部分等于零,式(4)求解起来比较麻烦。因此可以构造一个与目标函数水平的参数序列,再通过迭代方式求得参数序列{vt,t≥0}和水平序列{rt,t>0}。

通过以上操作,依次得到了最优引用参数v*和零方差概率密度函数的近似函数f(.;v*)。这样近似函数f(.;v*)的函数值比原先的随机变量的概率分布大得多,从而达到了把小概率事件转变成大概率事件的目的。得到的近似函数的方差比原先小很多,从而提高抽样的效率[7]。

1.3 分散抽样方法的原理

1) 按照变电站中元件强迫停运概率,把区间[0,1]等分成d段(d取2)。同时d需要满足1/d≥max{f1,f2,…,fn} (f1,f2,…,fn为系统元件的强迫停运率)。

2) 取服从均匀分布的随机数R,判断区间内元件i的状态。

2 改进的蒙特卡洛算法

在对交叉熵重要抽样法和分散抽样法进行研究后,利用各自的优点,本文提出一种改进的蒙特卡洛抽样算法。交叉熵重要抽样法通过Kullback-Leibler距离构造近似函数f(.;v*),可以把原本系统极小的小概率事件{S(X)≤r}转换成相对较大的概率事件。这样就减少了系统抽样次数,并且减小了近似函数f(.;v*)的方差,提高了蒙特卡洛的仿真效率。将系统的状态分成几个区间,每个区间内的随机数也不确定,但是都能表示系统的状态。通过对每个随机数进行仿真,得出相应的风险指标,在保证计算精度的前提下,减少迭代次数,提高抽样效率。经过实验验证,在分散抽样区间的选择上,且保证一定计算精度的前提下,选择2到4个区间即可,并不是区间越多效果越好。

使用Matlab语言实现改进算法的流程如图1所示。

图1 仿真流程图

其算法程序如下:

1) 初始化下列参数:抽样次数N,分位数ρ,平滑系数α,分散抽样的段数h,最大迭代次数M和LOLP方差系数β。

2) 令V0=μ,K=1,对交叉熵最优化进行重复计算。

3) 由分布密度函数Xi生成随机样本X1,X2,…,XN。利用函数S(Xi)计算每一个抽样状态Xi,并对其进行从大到小排序,其中S(Xj)表示序列S(X1)≥S(X2)≥…≥S(XN)中的第j个统计值。

5) 更新参数vk,再用相同方法进行抽样计算。

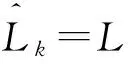
7) 令分散抽样的迭代次数N2=0。

9) 根据分散抽样原理进一步评估系统的状况。

10) 进一步计算LOLP和EPNS的指标和方差系数,判断收敛系数β是否满足,若β<βlolp,则停止计算,否则跳回步骤8)。

3 算例分析

本文风险性指标为停电功率期望值EPNS和系统停电概率LOLP。

系统停电概率LOLP为

式中:FLOLP(Xi)为在系统状态Xi下的切负荷(当为1时,系统是切负荷状态)。

停电期望功率EPNS为

式中:FEPNS(Xi)为系统状态Xi时的切负荷量,单位MW。

通过对IEEE-RTS系统变电站部分做风险评估比较,用改进的蒙特卡洛抽样算法(方法IV)将得到的风险性指标值与其他三种方法进行对比(常规抽样法(方法I)、分散抽样法(方法II)、交叉熵重要抽样法(III))。方差系数β取不同值时,方法I、II、III、IV计算得到了各种数据结果如表1所示。

通过表1可以看出,方法IV的优势非常明显。以方差系数均为β=0.01进行对比,在抽样次数上,方法IV抽样次数最少,而且相对于方法II,抽样次数少近一半。在抽样时间上,方法Ⅳ只用了方法I近1/4时间,用了方法II的1/3时间。因此在方差系数一定的前提下,改进方法能够明显减少抽样次数、缩短仿真时间,有效加强控制人员对风险的快速应对。

表1 仿真结果

不同抽样次数下方法II和IV的EPNS方差系数的对比如图2所示,图中下方的那根曲线为方法IV的ηEPNS。

图2 不同抽样次数下方法II和IV的EPNS方差系数

从图2很容易看到,在抽样次数一定时,方法IV的EPNS方差系数明显低于方法II,方法IV提高了蒙特卡洛的收敛速度。以抽样50 000次为例,通过计算可以得到,方法II得到的方差系数ηEPNS为0.062 651 3,方法IV的方差系数ηEPNS为0.028 697 2,两者相差一倍,因此改进后的蒙特卡洛算法具有更快的计算速度。

4 结 论

在交叉熵重要抽样法的基础上引入分散抽样方法,发现改进的蒙特卡洛算法能够产生更多的故障状态,提高抽样效率,以较少的次数得到较高的模拟精度。通过实验对比可以看出,改进的蒙特卡洛算法能显著提高抽样效率,明显加快收敛速度,可作为一种可行有效的评估算法。

[1] 谢绍宇, 王秀丽, 王锡凡, 等.自适应重要抽样技术在发输电系统可靠性评估中的应用[J].电力系统自动化, 2010, 34(5):13-17.XIE Shaoyu, WANG Xiuli, WANG Xifan, et al.Application of adaptive importance sampling technique in reliability evaluation of composite generation and transmission system[J].Automation of Electric Power Systems, 2010, 34(5):13-17.

[2] 宋晓通, 谭震宇.改进的重要抽样法在电力系统可靠性评估中的应用[J].电网技术, 2005, 29(13):56-59.SONG Xiaotong, TAN Zhenyu.Application of improved importance sampling method in power system reliability evaluation[J].Power System Technology, 2005, 29(13):56-59.[3] 石文辉, 别朝红, 王锡凡.大型电力系统可靠性评估中的马尔可夫链蒙特卡洛方法[J].中国电机工程学报, 2008, 28(4):9-15.SHI Wenhui, BIE Zhaohong, WANG Xifan.Applications of Markov Chain Monte Carlo in large-scale system reliability evaluation[J].Proceeding of the CSEE,2008,28(4):9-15.

[4] 郭袅, 边二曼, 徐冰亮.黑龙江省电网静态风险评估[J].黑龙江电力, 2014, 36(1):54-57.GUO Niao, BIAN Erman, XU Bingliang.Static risk evaluation for Heilongjiang grid[J].Heilongjiang Electric Power, 2014,36(1):54-57.

[5] 别朝红, 王秀丽, 锡凡.电力系统可靠性评估的混合法研究[J].中国电力, 2001, 34(3):26-29.BIE Zhaohong, WANG Xiuli, WANG Xifan.Study of hybrid method on power system reliability evaluation[J].Electric Power, 2001,34(3):26-29.

[6] 王晶, 李岩, 张海鹰, 等.基于改进抽样方法的电力系统可靠性评估研究[J].仪表技术, 2015(9):36-38.WANG Jing, LI Yan, ZHANG Haiying, et al.Research on power system reliability evaluation based on improved sampling method[J].Instrumentation Technology,2015(9):36-38.

[7] 王景辰, 李孝全, 杨洋, 等.基于交叉熵的蒙特卡洛法在发电系统充裕度评估中的应用[J].电力系统保护与控制, 2013, 41(20):75-79.WANG Jingchen, LI Xiaoquan, YANG Yang, et al.Application of Monte Carlo simulation based on cross-entropy methods in generating system adequacy evaluation[J].Power System Protection and Control, 2013,41(20):75-79.

[8] 何国锋, 谭震宇.采用等分散抽样法的电力系统概率仿真[J].电力自动化设备, 2004, 24(7):57-59.HE Guofeng, TAN Zhenyu.Power system probabilistic simulation using average and scattered sampling[J].Electric Power Automation Equipment, 2004,24(7):57-59.

(责任编辑 张兴业)

Application of improved Monte Carlo algorithm in substation risk assessment

YANG Jieming1,LI Zhaocheng1,GUO Tong2

(1.School of Information Engineering, Northeast Dianli University, Jilin 132012, China; 2.Fujian Electric Power Engineering Contract Firms, Fuzhou 350005, China)

Aiming the problems of the traditional non-sequential Monte Carlo sampling method in power system risk evaluation, such as repeated sampling and long period of simulation, this paper proposed the improved Monte Carlo algorithm.It is a method that firstly formulates the zero-variance approximate function of each element to get their optimal parameters, and then samples by scattered sampling method.Through the combination of the two methods, scattered sampling and Monte Carlo, the sampling efficiency of Monte Carlo is enhanced, as well as the calculation speed.Compared with the traditional sampling methods (scattered sampling and cross-entropy method) based on the IEEE RTS substation, the improved method has an advantage in little probability event.

substation;risk assessment;Monte Carlo;Scattered sampling method;importance sampling

2016-04-22;

2016-06-13。

国家自然科学基金资助项目(51277023);吉林省科技发展计划资助项目(20140204071GX)。

杨杰明(1972—),男,教授,主要研究方向为电力信息化、数据挖掘、数据预处理。

TM63

A

2095-6843(2016)05-0423-04