基于数据驱动的模糊系统辨识研究

王新超, 钱烽雷

(中国能源建设集团 江苏省电力设计院有限公司,江苏 南京 211102)



基于数据驱动的模糊系统辨识研究

王新超, 钱烽雷

(中国能源建设集团 江苏省电力设计院有限公司,江苏 南京 211102)

针对实际中某些过程无法确定其精确表达式的问题,研究了基于输入-输出数据的模糊建模方法。采用Mamdani模型和模糊基函数,以系统的输入-输出数据为基础,通过One-Pass、误差反向传播、查表法、最小二乘法这4种基于数据驱动的建模方法分别建立了Mackey-Glass混沌系统的模糊模型,用Mackey-Glass混沌数据验证了它们的有效性和实用性。对这4种方法的性能和适用场合做了分析说明,为实际过程的建模提供参考依据。在实际中,可根据需要选择合适的建模方法。

模糊基函数; 模糊建模; 反向传播; 最小二乘

1 引 言

模糊辨识在自动化领域逐渐得到了广泛的研究与应用。其通过IF-THEN规则,建立未知系统的数学模型。在实际中,IF-THEN规则的确定可通过显性知识和隐性知识。对于显性知识,可通过专家知识去描述模糊IF-THEN规则,从而建立模糊系统。而隐性知识则是通过对黑箱系统的输入-输出进行采集,通过一定的输入输出数据建立模糊系统。目前,使用较多的模糊规则模型主要为Mamdani模型和T-S模型,两者都在实际中取得了较为广泛的应用。两者的前件部分都是一样的,区别在于Mamdani模型的后件部分为模糊集合,而T-S模型的后件为线性方程式。

模糊推理系统的模糊推理机、模糊化操作和解模糊化操作有多种选择。比如推理机可分为乘积推理机、最小推理机、Lukasiewciz推理机、Zadeh推理机、Dienes-Rescher推理机等。模糊化操作可包括单点模糊化、高斯模糊化、三角形模糊化等。解模糊化操作包括重心解模糊化、中心平均解模糊化、最大值解模糊化等[1]。本文采用Mamdani模型和模糊基函数,以系统的输入-输出数据为基础,通过4种基于数据驱动的建模方法建立了Mackey-Glass混沌系统的模糊模型。

2 模糊基函数

Mamdani模糊模型第l条规则表示如下:

模糊推理系统如图1所示[2]。

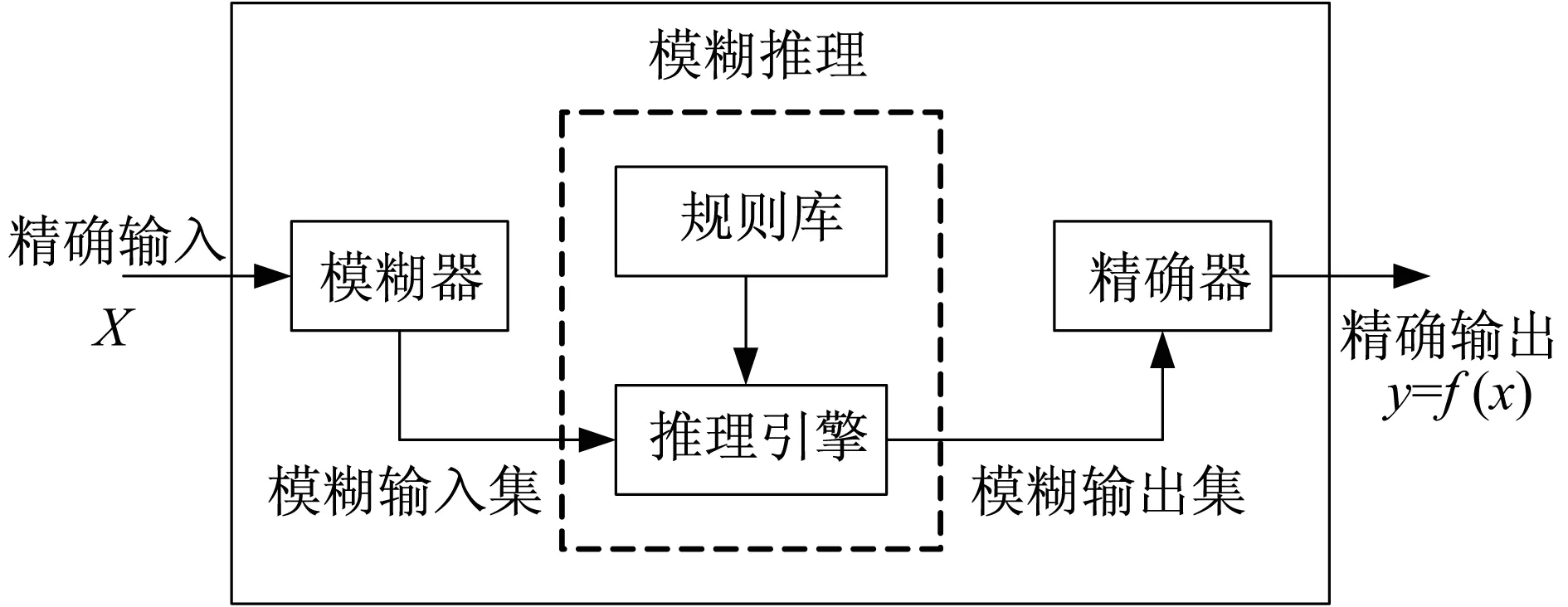
图1 模糊推理系统Fig.1 Fuzzy inference system

单点模糊化,其将一个给定输入x*映射成模糊集合U上的一个模糊单值A′,A′在x*上的隶属度值为1,其它所有点上的隶属度为0,表示如下:

中心平均解模糊化可由下式确定:

(1)

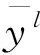
在模糊器采用单点模糊器,乘积推理机和中心平均解模糊化的时候,模糊系统的输出可表示为:

(2)

3 模糊系统辨识框架

考虑如下离散非线性系统:

y(k+1)=f(y(k),…y(k-n+1),

u(k),…,u(k-m+1))

式中,f是需要辨识的未知函数,u和y分别为系统的输入和输出,n和m为正整数。我们的任务是要利用模糊逻辑系统来辨识未知函数f。文献[4]指出,有两种方案对f进行辨识:

(1) 并行模型

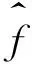
(2) 串行-并行模型

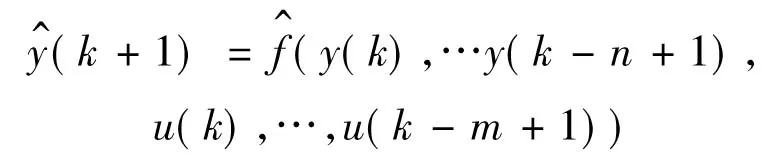
这里,不使用模糊系统的输出。

两种方案的区别是:并行模型中,模糊辨识模型的输出要反馈回辨识模型;而串行-并行模型中则将要辨识系统的输出反馈给辨识模型。图2和图3显示了两种辨识方案的基本框架图。文献[4]指出,串行-并行模型要优于并行模型,本文选用串行-并行模型。

4 基于数据驱动的模糊辨识方法

给定的N组输入-输出数据(xi,yi),i=1,2,…,N,下面介绍4种方法对其进行模糊辨识。

4.1 One-Pass

该方法每一组输入-输出数据建立一条if-then规则,如果选择了M数据,那么建立M条规

图2 并行辨识系统框架Fig.2 Framework of parallel identification system

图3 串行-并行辨识系统框架Fig.3 Framework of serial-parallel identification system

则[5]。比如针对Mamdani模糊模型的第l条规则:

4.2 误差反向传播法

该方法的前件参数和后件参数事先未知,通过误差反向传播学习算法来确定。该方法确定的模糊系统f(x),要使得式3)的拟合误差最小:

(3)

则:

其中,l=1,2,…,M,i=1,2,…,N。具体推导过程和初始参数的选择见文献[6]。

4.3 查表法

查表法首先要对输入-输出数据进行空间划分,则其前件参数和后件参数在辨识开始之前要事先确定,其过程如下:

(1) 对输入-输出进行模糊划分,本文选用的隶属函数为三角形隶属函数;

(2) 对训练的每对输入-输出数据产生一条模糊规则;

(3) 对步骤2的每条规则赋予一个强度,使得冲突的规则只保留强度最大的,这样不仅冲突解决了,规则数目也大大减少;

(4) 创建模糊规则库;

(5) 基于模糊规则库构造模糊系统。

关于每个步骤的具体说明可参考文献[1]。

4.4 最小二乘法

如果在模糊辨识之前,前件参数已经给定,也即式2)可表达为

y=Pθ

这里:

y=[y1,y2,…yN]T

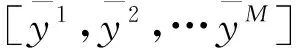
最小二乘也就是求取θLs,使得式4)取得最小值:

(4)

许多文献中提出了各种改进的最小二乘法,本文使用一般的最小二乘法,也即直接最小二乘和递推最小二乘。直接最小二乘的求取公式如下:

θLs=(PTP)-1PTy

递推最小二乘的求取公式如下:

递推最小二乘的初始条件为θLs=0,S0=βI,β一般取大于10000的实数,I是M×M的单位矩阵。

5 仿真试验

本文选取的辨识模型为Mackey-Glass混沌模型,其离散以后的表达式如下[7]:

本文选取τ=30,模糊辨识模型选择:y(t)=f(y(t-1),y(t-2),y(t-3),y(t-4)),y(0)～y(30)赋初值为1.2。在t=1000和t=2000之间选择1000对输入-输出数据作为训练数据和检验数据,辨识精度通过均方误差平方根(RMSE)来描述:

5.1 One-Pass仿真结果

选用500组训练数据,那么规则数为500条。利用高斯隶属函数,前件参数的选择如3.1节描述,宽度为0.1。图4显示了本算法的模糊模型和混沌时间序列的拟合曲线,其中实线表示实际输出。

500对检验数据的RMSE=0.0439。

5.2 反向传播仿真结果

选用500组训练数据,规则数确定40。利用高斯隶属函数,初始参数的选择与One-Pass方法相同,宽度为0.1。图5显示了本算法的模糊模型和混沌时间序列的拟合曲线,其中实线表示实际输出。

图4 One-Pass法模糊模型输出与实际输出拟合曲线Fig.4Fuzzy model output of One-Pass method and actual output fitting curve

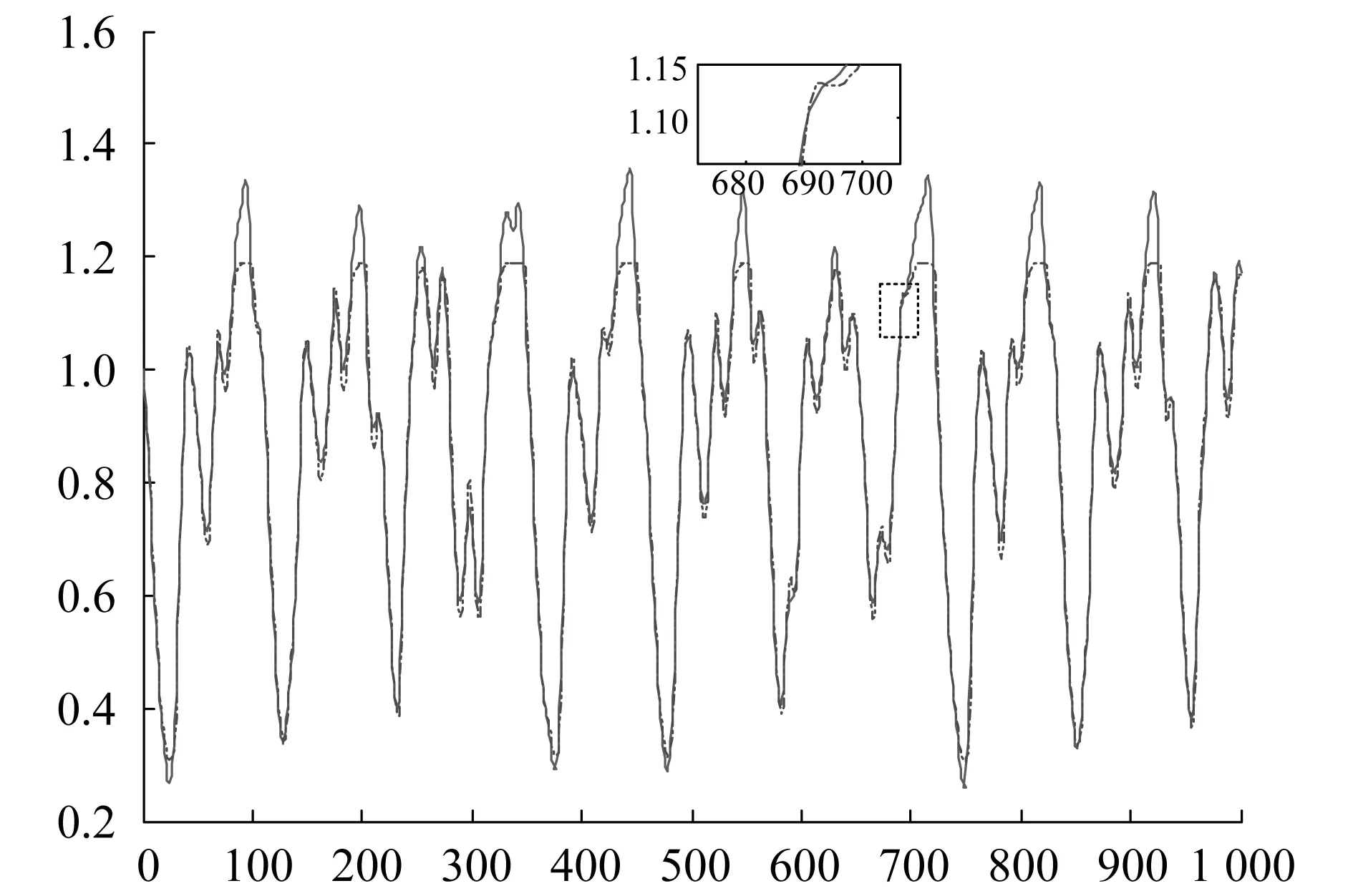
图5 反向传播法模糊模型输出与实际输出拟合曲线Fig.5Fuzzy model output of back propagation method and actual output fitting curve

500对检验数据的RMSE=0.0393。

5.3 查表法仿真结果

选用500组训练数据,隶属函数选择三角形隶属函数,经过规则冲突检查后,有效的规则数为45条,规则数大大减少。图6显示了把输入输出空间划分为7个的隶属函数图。

图7显示了本算法的模糊模型和混沌时间序列的拟合曲线,其中实线表示实际输出。

500对检验数据的RMSE=0.0278。

5.4 最小二乘法仿真结果

选用500组训练数据,规则数确定为40,选用递推最小二乘。利用高斯隶属函数,前件参数的选择与One-Pass方法相同,宽度为0.1。图8显示了本算法的模糊模型和混沌时间序列的拟合曲线,其中实线表示实际输出。

图6 三角形隶属函数Fig.6 Triangular membership function

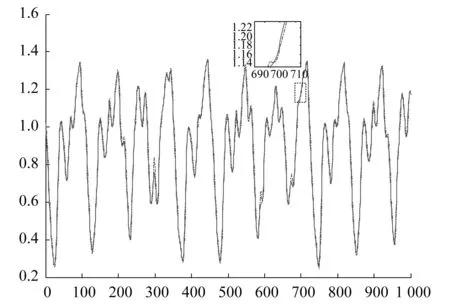
图7 查表法模糊模型输出与实际输出拟合曲线Fig.7 Fuzzy model output of table-seeking method and actual output fitting curve

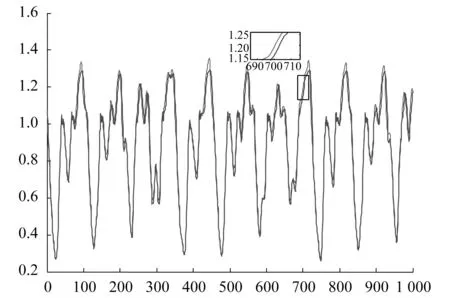
图8 递推最小二乘法模糊模型输出与实际输出拟合曲线Fig.8Fuzzy model output of recursive least squares method and actual output fitting curve

500对检验数据的RMSE=0.0429。如果规则数增加,则相应的精度也会增加。

6 结 语

本文利用模糊基函数,在给定输入-输出数据的情况下,基于这些输入-输出数据建立了系统的模糊模型。通过几种不同的方法建立模糊模型,说明基于数据驱动的模糊辨识方法的有效性与实用性。

通过仿真实验,One-Pass法其选择了多少训练数据,就产生相应的规则数目,而经过查表法的筛选,其规则数大大减少,而当划分区间进一步增加的时候,辨识精度也会提高。误差反向传播方法对每一对训练的数据进行参数计算,保证了当前数据点的误差最小,可用于在线建模与控制。而最小二乘法使得所有数据点的误差和达到最小,其精度增加。在使用直接最小二乘的时候,由于在参数求取的时候有求逆过程,有可能矩阵的逆不存在,导致参数求取失败,在仿真试验的时候也出现过这种情况,而递推最小二乘法则不存在这一问题。在实际中,可根据需要选择合适的建模方法。

[1] 王立新.模糊系统与模糊控制教程[M].2003.

WANG Lixin.A Course in Fuzzy Systems and Control[M].2003.

[2] 陈薇,孙增圻.二型模糊系统研究与应用[J].模糊系统与数学,2005,19(1):126-135.

CHEN Wei,SUN Zengqi.Research and application on TypeⅡ Fuzzy system[J].Fuzzy Systems and Mathematics,2005,19(1):126-135.

[3] WANG L X,Mendel J M.Fuzzy basis functions,universal approximation,and orthogonal least-squares learning[J].IEEE Transactions on Neural Networks,1992,3(5):807-814.

[4] Narendra K S,Parthasarathy K.Identification and control of dynamical systems using neural networks[J].IEEE Transactions on Neural Networks,1990,1(1):4-27.[5] Mendel J M,Mouzouris G C.Designing fuzzy logic systems[J].IEEE Transactions on Circuits and Systems-Part II-Analog and Digital Signal Processing,1997,44(11):885-895.

[6] WANG L X,Mendel J M.Back-propagation fuzzy system as nonlinear dynamic system identifiers[C].Fuzzy Systems,1992.IEEE International Conference on.IEEE,1992:1409-1418.

[7] LO J,CH Yang.A heuristic error-feedback learning algorithm for fuzzy modeling[J].IEEE Translation on Systems Man and Cybernetics,1999,29(6):686-691.

Research on Fuzzy System Identification Using Data Drive

WANGXinchao, QIAN Fenglei

(Jiangsu Power Design Institute Co.,Ltd.of China Energy Engineering Group,Nanjing 211102,China)

Due to the difficulty in getting the exact expression of some actual processes,fuzzy modeling method by input-output data is discussed in this paper.One-pass,back propagation, seeking table and least square are used to build Mackey-Glass chaos fuzzy model by Mamdani fuzzy model and fuzzy basic function,which based on input-output datas.The effectiveness and practicality of these four methods are illustrated by Mackey-Glass chaos data.The performance and application conditions of these four methods are stated,providing reference for actual modeling.In practice, a suitable modeling method can be selected according to actual process.

fuzzy basic function; fuzzy modeling; back propagation; least square

王新超 男(1987-),安徽宿州人,工程师,硕士,主要从事电站自动化设计工作和先进控制理论及应用研究。

钱烽雷 男(1980-),江苏启东人,工程师,主要从事电站自动化设计工作。

TP 273

A