具有服务等级的可拒绝平行机排序问题

荣 建 华

(石家庄铁道大学四方学院 基础部， 河北 石家庄 051132)



具有服务等级的可拒绝平行机排序问题

荣 建 华

(石家庄铁道大学四方学院 基础部， 河北 石家庄 051132)

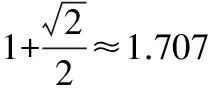
在线排序；平行机；拒绝费用；竞争比；服务等级

0 引 言

排序问题是运筹学与组合优化领域一类重要的问题，对排序理论的研究具有重要的理论意义和广阔的应用前景.近年来，在含多个窗口的服务业，如银行等领域，经常存在以下2种现象：首先，提供服务的机构通常有多个不同等级的窗口，如一般窗口、贵宾窗口；顾客也有不同的级别，如一般会员、金卡会员、银卡会员.等级低的窗口为所有顾客服务，等级高的窗口只为高级别的顾客服务.其次，服务存在双向选择，提供服务的一方为了考虑总体效益，可以提供服务需求，花费一定的服务成本；顾客也会因为得不偿失而拒绝需求，但此时要付出拒绝费用，最终希望整体利益达到最优.工件带有拒绝费用和服务等级的排序问题是现代工业生产中出现的2个新的组合优化模型，近年来受到许多研究人员的关注.本文将工件可拒绝与具有服务等级2个模型复合起来，即研究具有服务等级的可拒绝平行机在线排序问题.基本问题描述如下：假定有2台平行机M1,M2，加工速度一致；n个工件J1,J2,…,Jn,分别按列表在线到达，每个工件Jj含有3个参数：加工长度tj，拒绝费用pj以及服务等级gj=1,2.当工件到达时，可以接收加工，占用一定的加工时间；也可以拒绝，付出相应的罚值.进一步，如果工件被接收，则等级gj=1的工件只能分配在机器M1上加工；等级gj=2的工件被分成2两部分，分别被安排到机器M1，M2上加工.目标为被接收工件的最大完工时间(makespan)与被拒绝工件的总罚值之和最小.为此本文设计了在线算法PH.

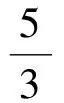
1 P2|gj=2,online|W的算法设计

为便于分析算法，下面引入一些常用的记号：

A、R：算法中分别被接收和拒绝的工件集；

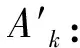
A″k：算法中被接收最优解中被拒绝的等级为k的工件集；

R′：算法和最优解中均被拒绝的工件集；

R″k：算法中被拒绝最优解中被接收的等级为k的工件集；

L(S),S⊆J∶S中工件的总长度；

P(S),S⊆J∶S中工件的总罚值；

C(E)：算法中将E作为被加工工件集时的最长完工时间；

C*(E)：最优解中生成的最长完工时间；

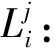
WPH：算法生成的目标值；

W*：最优解中生成的目标值.

下面给出在证明竞争比过程中非常有用的几个引理.

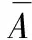
其中tmax为A中最大工件的长度.

引理2[8]设Q=(1,1,…,1)T，K=(k1,k2,…,ku)为1×u矩阵，X=(x1,x2,…,xn)T为u×1矩阵，P=(pij)u×u为可逆矩阵，其中第j行行向量记作αj.如果KP-1≥0,则∀X≥0，均有KX≤(KP-1Q)max{α1X,α2X,…,αuX}.

由引理2可得

下面给出在线算法PH的具体描述：

当工件Jj到达时,

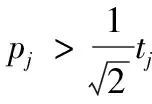
规则G1：若gj=1，则将工件Jj分配给机器M1加工；

引理4 设A为被加工的工件集，A中等级为1的工件总是分给M1加工，等级为2的工件按G2规则加工，令x为A中最后一个被加工的工件，则下列结论成立：

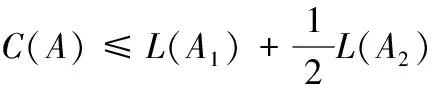
证明 (i)如果分配到M1上的均为等级为1的工件，则

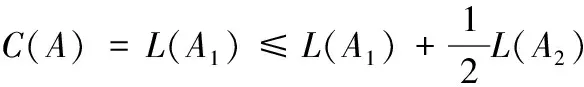
(1)

否则，至少存在一个等级为2的工件部分分配在M1上加工，令y为最后一个分配在M1上具有等级2的工件.不妨令ty1=(1-λ)ty，ty2=λty，λ∈(0,1)，并分别将其分配给M1，M2加工，Lxy为工件x,y之间机器M1的负载(不含x,y的长度)，则

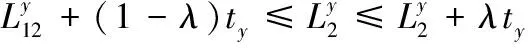
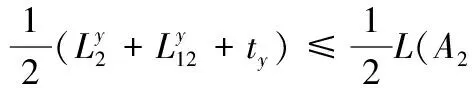
(2)

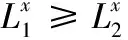
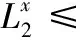
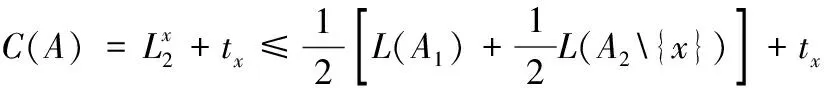
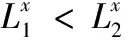
C(A)=

证明 情形1 若A=φ，算法将所有工件拒绝，于是

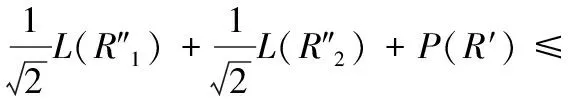
情形2.2 若gx=2，由引理4可知，

于是有

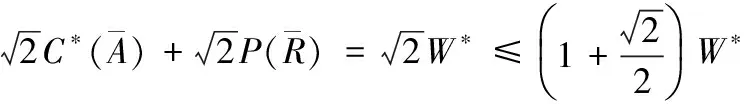
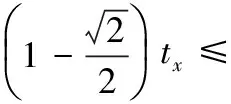
证毕！

2 结 语

研究了复合服务等级和可拒绝2种模型的2台平行机排序问题，在工件被接收加工的情形下，等级为2的工件允许被拆分.文中设计了在线算法PH，并证明了其竞争比为1.707，下界为1.618，上下界差约0.089.下一步将致力于构造更精确的算法，以进一步缩小上下界差.

[1] BARTAL Y, LEONARDI S, MARCHETTI-SPACCAMELA A, et al. Multiprocessor scheduling with rejection[J]. SIAM J on Discrete Mathematics,2000,13:64-78.

[2] HE Y,MIN X.On-line uniform machine scheduling with rejection[J]. Operations Research Transactions,2009,13(1):29-36.

[3] DOSA G, HE Y. Preemptive and non-preemptive on-line algorithms for scheduling with rejection on two uniform machines[J]. Computing,2006,76:149-164.

[4] JIANG Y W, HE Y, TANG C M. Optimal online algorithm for scheduling on identical machines under a grader of service[J]. Journal of Zhejiang University: Science A,2006,7(3):309-314.

[5] PARK J, CHANG S Y, LEE K. Online and semi-online scheduling of two machines under a grader of service provision[J]. Operations Research Letters,2006,34:692-696.

[6] JIANG Y. Online scheduling on parallel machines with two GoS levels[J]. Journal of Combinatorial Optimization,2008,16:28-38.

[7] ZHANG A, JIANG Y, TAN Z. Online parallel machines scheduling with two hierarchies[J]. Theoretical Computer Science,2009,410:3597-3605.

[8] TAN Z, ZHANG A. A note on hierarchical scheduling on two uniform machines[J]. Journal of Combinatorial Optimization, 2010,20:85-95.

RONG Jianhua

(DepartmentofBasic,ShijiazhuangTiedaoUniversitySifangCollege,Shijiazhuang051132,China)

Parallel machine scheduling with service hierarchy and rejection. Journal of Zhejiang University(Science Edition), 2016,43(6):685-688

on-line scheduling; parallel machine; penalty of rejection; competitive ratio; hierarchical

2015-12-18.

河北省高等教育教学改革研究与实践项目(2015GJJG293)；河北省高等教育科学研究课题(GJXH2015-291).

荣建华(1981-)，ORCID:http://orcid.org/0000-0002-7147-4866，女，硕士，讲师，主要从事组合优化、排序理论研究,E-mail:rongjianhua2006@126.com.

10.3785/j.issn.1008-9497.2016.06.012

O 223

A

1008-9497(2016)06-685-04