求解一类投资组合问题的半光滑New ton法

郑华，姚智丽，周洁

（韶关学院数学与统计学院，广东韶关512005）

求解一类投资组合问题的半光滑New ton法

郑华，姚智丽，周洁

（韶关学院数学与统计学院，广东韶关512005）

给出求解一类投资组合问题的半光滑New ton法，并对算法进行收敛性分析，数值例子表明新方法的高效率.

投资组合问题；半光滑New ton法；线性互补问题

著名的Markowitz投资组合优化理论是金融统计分析中的重要内容，该理论表明，在收益和风险的权衡中，投资者采用如下策略：在期望收益相同的条件下，选择风险最小的证券.即是在给定预期收益水平的情况下，对期望风险进行最小化.

1　预备知识

在不允许卖空的假设下，Markowitz投资组合优化理论可以转化为以下二次规划问题：

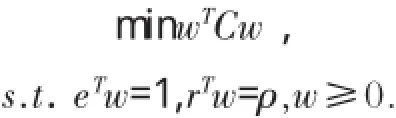
这里C表示投资组合中的资产收益率的协方差矩阵，w表示投资组合的权重向量，代表的是各资产中投资的资本量，r表示不同资产的预期收益率向量，ρ表示给定的总回报，e表示全1的列向量.设w是该二次规划的局部最优解，根据Karush-Kuhn-Tucker最优性定理，存在Lagrange乘子向量y，满足K-K-T条件：

其中B=(e r)T,d=(-1 1)T定义：

就得到了线性互补问题(Linear Complementarity Problem)，记为LCP(q,A).

对给定的A∈Rn,求解z∈Rn满足:

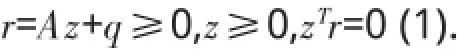
这是一个特殊的优化问题，许多学者给出了求解LCP(q,A)的各种数值算法，这方面的综述参看文献[1].本文充分利用投资组合问题中系统矩阵的特殊性，设计新的数值算法.

2　半光滑New ton法

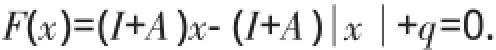
其中I为单位矩阵.基于上述模方程，Zheng和Li在文献[3]中引入广义导数构建了求解LCP(q,A)的半光滑Newton法：

算法1(求解F(x)的半光滑Newton法)给定初始向量x(0),进行以下迭代直至收敛：

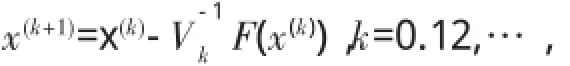
其中Vk是F(x)的一个广义导数,定义如下：

定义1如果n阶方阵A的所有主子阵非奇异，称A为P-矩阵［4］.

引理1如果n阶方阵A是正定矩阵，那么A为P-矩阵［2］.

引理2如果A是P-矩阵，那么求解(2)的算法1局部平方收敛的.特别地,如果F(x)=0的真实解没有0分量，那么对任给的初值，算法1二步收敛［3］.

考虑用算法1求解投资组合问题转化得到的LCP(q,A)，就有如下定理.

定理1在不允许卖空的规定下，如果资产收益率的协方差矩阵C为正定矩阵，那么利用算法1求解(2)是局部平方收敛,特别地，如果投资者在证券市场中对所有证券都保持持有，那么算法1求解(2)二步收敛.

如果投资者在证券市场中对所有证券都保持持有，根据相关的符号约定，这意味着(2)的解中没有0分量，由引理2可知，此时算法1是二步收敛的.

证毕.

注1定理1表明，利用算法1求解投资组合问题转换得到的LCP(q,A)是可行的并具有高效性.

3　数值试验

接下来通过数值试验展现算法1的高效性.从国泰君安数据库中提取清华紫光、苏宁电器、中国船舶、招商地产、五粮液这5支股票3年共151个星期的个股回报率数据，经过计算所得的协方差矩阵和平均收益率向量分别为：

设定预期收益率为1.2%,我们分别利用算法1和经典的Lemke算法［2］求解上述证券投资问题，都可以计算得到最优投资组合比例向量为：

两种算法的运行效率对比为：

(1)Lemke算法：运行时间0.038 4秒，结果误差为0；

(2)算法1：运行时间0.003 7秒，结果误差为2.309 7×10-16.

从上述效果的对比来看，算法1比Lemke算法运行更快.因为Lemke算法是直接法，所以它的结果误差为0是必然的，虽然算法1的结果误差未达到0，但2.309 7×10-16的误差精度也可以足够满足实际的需求.

［1］韩继业，修乃华，戚厚铎.非线性互补理论与算法[M].上海:上海科学技术出版社，2006.

［2］Cottle R W，Pang J S,Stone R E.The Linear Com plementarity Problem[M].Philadelphia：SIAM Publisher，2009.

［3］Zheng H，Li W.The modulus-based nonsmooth Newton's method for solving linear complementarity problems［J］.Journal of Computational and Applied Mathematics，2015（288）:116-126.

［4］Berman A，Plemmons R J.Nonnegative matrix in the mathematical sciences[M].Philadelphia:SIAM Publisher，1994．

A Sem i-sm ooth New ton’s M ethod for Solving the Portfolio Problem

ZHENG Hua，YAOZhi-li，ZHOU Jie
（School ofMathematicsand Statistics，Shaoguan University，Shaoguan，512005，Guangdong，China）

A semi-smooth Newton’s method for solving the portfolio problem is established.The convergence analysis isgiven.Numerical example shows that thenewmethod isefficient.

portfolio problem;semi-smooth Newton’smethod;linear complementarity problem

O151.21

A

1007-5348（2016）08-0004-03

2016-07-08

韶关学院科研项目(SY2014KJ01)；韶关学院大学生创新创业训练项目(201610576017).

郑华（1982-），男，广东韶关人，韶关学院数学与统计学院讲师，博士；研究方向：计算数学.

（责任编辑：邵晓军）