足底压力中心不对称性适宜计算方式的探讨
刘丽玲,倪朝民,岳 童,刘 孟,刘 郑,陈 进,王 丽,许凤娟,曾林芳
◇经验与体会◇
足底压力中心不对称性适宜计算方式的探讨
刘丽玲,倪朝民,岳 童,刘 孟,刘 郑,陈 进,王 丽,许凤娟,曾林芳
探讨脑卒中患者步行时不同足底压力中心(COP)时空参数对称性比的适宜计算方式。选取33例脑卒中患者进行步态测试,使用3种方法计算COP时空参数的对称性比,并分析对称性比与步速的相关性。计算方式影响对称性比与步速的相关性,为了更加客观地反映步速与不对称性的相关性,对于单、双支撑期COP时空参数,可分别选用患侧除以健侧相应参数、两者中的较小值除以较大值计算对称性比,必要时根据散点图选择适宜计算方式或进行亚组分析。
卒中;步态障碍;神经性;足底压力中心;步速;步态不对称性
由于患侧肢体感觉及运动功能障碍,脑卒中患者常表现为步速下降、患侧下肢负重能力下降、重心偏向健侧的不对称模式[1-4]。步速和不对称性均与脑卒中患者运动功能障碍程度相关,是反映脑卒中患者肢体功能恢复的良好指标[1,5],且步速增加及步行模式的改善也是脑卒中患者康复治疗的重要目标[6]。步速是反映步行能力及影响日常生活能力的重要指标,而不对称性可以反映步行质量,与平衡能力及步行稳定性有关,且两者存在相关性[2,7-9]。但不同研究中不对称性表示方法各异,给不同研究的比较及循证医学的实施带来了困难,基于此,有学者比较了不同不对称性表示方法的区别,并推荐使用对称性比表示时空参数的不对称性[9]。但对称性比也有多种计算方式,关于对称性比不同计算方式的比较,尚未见详细报道。该研究以脑卒中患者步行时足底压力中心(center of pressure,COP)时空参数不对称性与步速相关性为例,比较不同对称性比计算方式的优缺点,探讨不同参数对称性比的适宜计算方式。
1 材料与方法
1.1 病例资料 选取2013年9月~2015年2月安徽医科大学附属省立医院康复医学科收治的脑卒中患者33例。其中男26例,女7例;年龄37~66(52.09±9.07)岁,身高(168.42±4.18)cm,体重(68.67±9.40)kg,平均病程(2.86±1.07)个月。脑出血10例,脑梗死21例,脑梗死合并出血2例;左侧偏瘫22例,右侧偏瘫11例。受试者均签署知情同意书。
纳入标准:① 经头颅CT或MRI检查证实,符合第4届全国脑血管病学术会议通过的脑卒中诊断标准[10],且为单侧病灶;② 首次发病;③ 患侧下肢Brunnstrom分期为Ⅲ~Ⅴ期;④ 在无辅助器具及外力辅助下能独立步行10 m以上。
排除标准:① 有严重心肺、肝、肾功能不全者;② 严重认知功能障碍[简明精神状态检查量表(MMSE)评分≤24分][3,7]或精神功能障碍不能配合实验者;③ 合并有其他影响步行能力的疾病,如帕金森病、骨关节疾病、美尼尔病及偏盲等;④ 存在脑干部位病变者。
1.2 测试仪器 采用安徽埃力智能科技有限公司生产的步态与平衡功能训练评估系统(AL-600型)进行步态测试,该系统由4块压力板(长×宽×厚为500 mm×400 mm×10 mm)、信息转换控制器、计算机和分析软件组成,压力板铺成长2 m的压力步道,采样频率为100 Hz。该系统将压力板上传感器的受力信号转化为数字信号后,通过计算机自动分析处理,生成相应的步态评估报告。
1.3 测试方法 在安静的室内环境下,受试者脱掉鞋袜以自然步速沿着步道的中线方向行走进行2次预测试,待受试者熟悉测试流程后开始测试。每次测试均从步道前2 m开始,穿过压力板后继续行走2 m,以保证匀速通过步道。所有受试者测试3次,2次测试间可休息5 min,取3次测量均值进行分析。
1.4 观察指标 测试指标主要包括步速、单支撑时间、双支撑时间、步长、单支撑期COP在前后方向的位移(anterior-posterior COP displacement during single-support phase,AP-COPDS)及速度(AP-COP velocity during single-support phase,AP-COPVS)、单支撑期COP在内外侧方向的位移(medial-lateral COPDS,ML-COPDS)及速度(medial-lateral COPVS,ML-COPVS)、双支撑期COP在前后方向的位移(AP-COPD during double-support phase,AP-COPDD)及速度(AP-COPV during double-support phase,AP-COPVD),双支撑期COP在内外侧方向的位移(medial-lateral COPDD,ML-COPDD)及速度(medial-lateral COPVD,ML-COPVD),左侧双支撑期是指右足触地开始至左足离地的时相,右侧同理[11],双支撑期COP指的是双足的压力中心。分别使用3种方式计算COP时空参数的对称性比,即公式一:对称性比=V患/V健,公式二:对称性比=V大/V小,公式三:对称性比=V小/V大,其中V患、V健、V大、V小分别代表患侧、健侧的步态参数及两者中的较大者、较小者,对称性比越接近于1,对称性越好。公式中V为变量。
1.5 统计学处理 采用SPSS 16.0软件进行分析,K-S检验结果显示,使用公式二时,部分对称性比不符合正态分布。当使用公式一、三时,采用Pearson相关性分析法分析对称性比与步速的相关性,当使用公式二时,采用Spearman相关性分析法,均为双侧检验。相关度划分标准[7]:|r|<0.4表示轻度线性相关,0.4≤|r|<0.7表示中度线性相关,|r|≤0.7表示高度线性相关。其中3例患者的公式二所得部分COP时空参数对称性比明显偏离均值(中位数)10倍标准差(四分位间距)以上,故将这3例患者的所有数据剔除后进行统计分析。
2 结果
2.1 单支撑期COP时空参数对称性比与步速的相关性 使用公式一时,所有的单支撑期COP时空参数对称性比均与步速呈正相关性(r1=0.480~0.716,P<0.01);使用公式二时,仅单支撑时间对称性比与步速呈中度负相关性(r2=-0.687,P<0.01);当使用公式三时,除AP-COPVS外,其他单支撑期参数对称性比均与步速呈正相关性(r3=0.387~0.715,P<0.05)。见表1。
2.2 双支撑期COP时空参数对称性比与步速的相关性 使用公式一时,AP-COPVD、ML-COPVD对称性比与步速呈负相关性(r1=-0.368~-0.443,P<0.05);使用公式二时,双支撑时间、AP-COPVD、ML-COPVD、步长对称性比与步速呈负相关性(r2=-0.458~-0.761,P<0.01);使用公式三时,除ML-COPDD外的其他双支撑期参数均与步速呈正相关性(r3=0.374~0.752,P<0.05)。见表2。
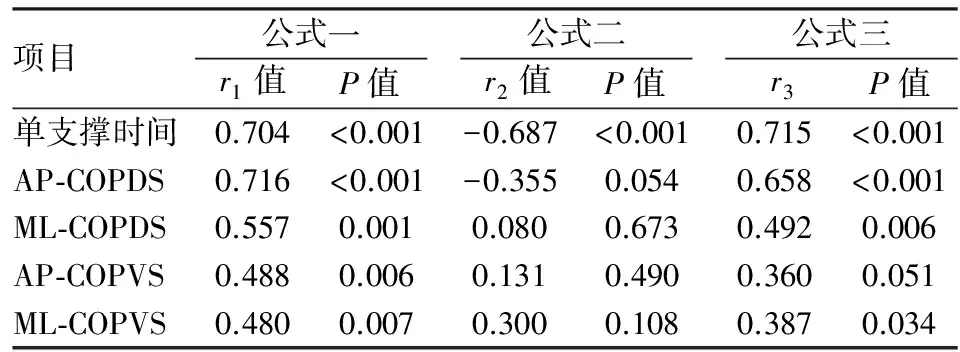
表1 3种不同计算方式下步速与单支撑期COP时空参数对称性比的相关性
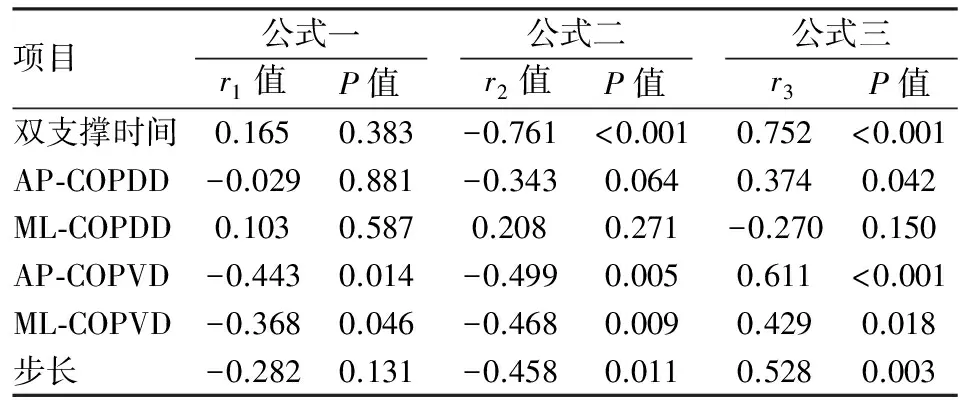
表2 3种不同计算方式下步速与双支撑期COP时空参数对称性比的相关性
2.3 双支撑时间对称性比与步速的相关性 当使用公式二、三时,双支撑时间对称性比与步速呈高度相关性(r2=-0.761,r3=0.752,P<0.01),但使用公式二时,出现偏离整体分布较远的值。使用公式一时,未发现相关性,但当步速小于21 cm/s时,两者呈正相关趋势,当步速大于21 cm/s时,两者呈负相关趋势。见图1、2、3。
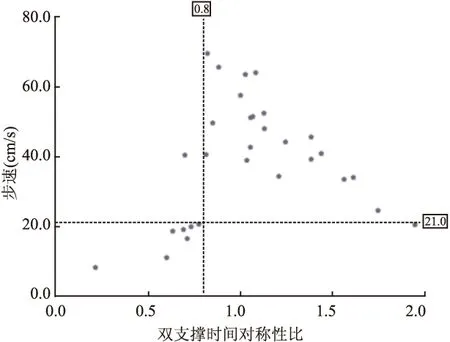
图1 使用公式一时步速与双支撑时间对称性比的关系
3 讨论
脑卒中患者步态不对称性可以反映步行质量,与运动功能障碍程度、平衡能力及步行稳定性相关,且长期不对称步态可能导致健侧肌肉骨骼疾患及患侧骨质疏松等问题[1,5,7-8,12]。步速可以反映步行能力,与生活自理能力相关[2],关于不对称性与步速的相关性,学者进行了大量的研究[1,8-9],然而不对称性表示方法的不一致给不同研究间的比较及循证医学的实施带来了困难。Patterson et al[9]以时空参数为例,发现不同表示方法所得结果相近,由于对称性比计算简单,易被理解,较被推荐使用。
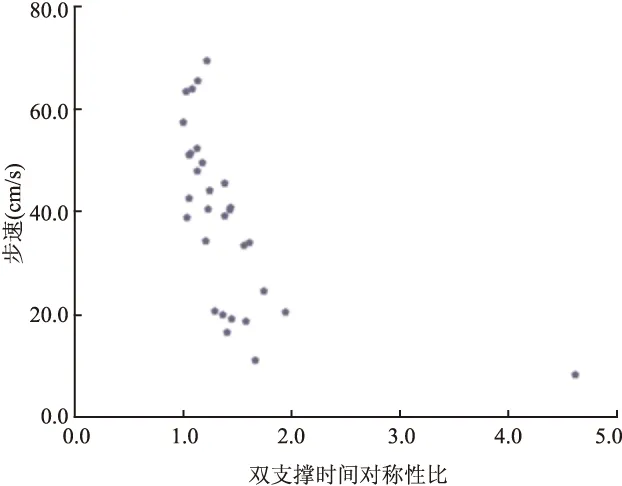
图2 使用公式二时步速与双支撑时间对称性比的关系
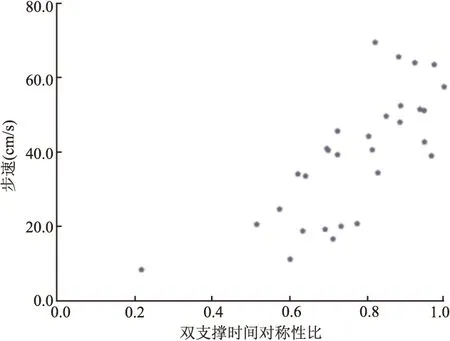
图3 使用公式三时步速与双支撑时间对称性比的关系
对称性比是反映不对称性的方式之一,即两侧下肢相应参数的比值,其值越接近于1,对称性则越好,包括患侧除以健侧相应参数,健侧除以患侧相应参数,较大值除以较小值,以及较小值除以较大值;前两者可以反映不对称性的方向,但当不对称性方向不一致时(即有的表现为患侧参数较大,有的则相反),不能比较不对称性的程度,且对称性比间的计算较困难[9,11]。后两者可以反映不对称性的程度,但不能反映不对称性的方向,且当参数的值较小时,较大值除以较小值存在将对称性比人为放大的风险,导致数据不符合正态分布,甚至出现个别值远远大于整体均值[13-14]。本研究也显示,3例患者的对称性比远远偏离整体分布,而不得不予以剔除。由于前两种计算方式意义相似,且脑卒中患者步态参数多表现为患侧小于健侧,为了减小对称性比被人为放大的风险,研究中不对健侧除以患侧相应参数进行讨论。
本研究显示,当使用公式一时,所有的单支撑期参数对称性比均与步速呈正相关性,使用公式三时,除AP-COPVS外,其余单支撑期参数对称性比均与步速呈正相关性。而使用公式二时,仅单支撑时间对称性比与步速呈负相关性。可见对于单支撑期参数,公式一、三较易发现不对称性与步速的相关性,且使用公式一时,所得相关度较高,可能与脑卒中患者单支撑期参数多表现为患侧小于健侧[1,4,15],导致公式一可同时反映不对称性的方向及程度,从而较易发现两者相关性有关。由于单支撑期参数数值上较小,使用公式二时,对称性比被人为放大的风险增加,从而掩盖了不对称性与步速的相关性。
当使用公式一时,仅AP-COPVD及ML-COPVD两者的对称性比与步速呈负相关性,而使用公式二、三时,大多数参数对称性比与步速存在相关性。可见对于双支撑期参数,公式一不易发现两者的相关性,而公式二、三可以,可能与双支撑期参数多表现为不对称性方向不一致有关,且有研究[1,9,11]显示双支撑时间、步长不对称性方向不一致。由于公式二有将对称性比人为放大的风险,当参数数值较小时,可使用公式三。这与Patterson et al[9]推荐较大者作为分子稍有不同,主要原因为其主要研究数值较大的时空参数,考虑当较大值作为分子时,对称性比均大于1,便于计算比较,而本研究主要探讨何种计算方式便于发现不对称性与步速的相关性,所研究的参数特点各异,且某些参数在数值上相对较小。
当使用公式二、三时,双支撑时间对称性比与步速分别呈高度负、正相关性,但使用公式二时,易出现偏离整体分布相对较远的值。使用公式一时,未显示相关性,但散点图提示当步速小于21 cm/s时,两者呈正相关趋势,即患侧双支撑时间相对越长,步速则越大,且对称性比均小于0.8,而当步速大于21 cm/s时,两者呈负相关趋势,且对称性比多大于0.8,也即说明双支撑时间对称性程度越好,步速则越大,从而解释了为什么使用不易反映不对称性程度的公式一时两者无相关性,而使用公式二、三时,两者呈高度相关性。这也提示当进行相关性分析时,可根据散点图特征选择合适的计算方式,必要时可进行亚组分析。
本研究为后期步态不对称性的研究及循证医学的实施提供了参考依据。对于单支撑期参数,公式一较易发现潜在的相关性,且公式一可以反映不对称性的方向,对步行机制的理解及临床康复的指导意义较大。而对于双支撑期参数,可使用公式三,必要时可根据散点图特征选择合适计算方式或进行亚组分析。公式二存在将不对称性放大的风险,当参数数值较小时,不推荐使用。本文仅研究了对称性比的3种计算方式,后期可进一步探讨针对不同步态参数,各种不对称性计算方式的区别及适宜计算方式。
[1] Patterson K K, Parafianowicz I, Danells C J, et al. Gait asymmetry in community-ambulating stroke survivors[J]. Arch Phys Med Rehabil, 2008, 89(2): 304-10.
[2] Perry J,Garrett M,Gronley J K,et al.Classification of walking handicap in the stroke population[J].Stroke,1995,26(6):982-9.[3] 杨 洁, 倪朝民, 尹傲冉, 等. 脑卒中偏瘫患者足底压力与步行时相的相关性[J]. 安徽医科大学学报, 2014, 49(4): 533-5,539.
[4] 刘丽玲, 倪朝民, 岳 童, 等. 脑卒中偏瘫患者步行时足底压力中心的特点[J]. 中华物理医学与康复杂志, 2015, 37(11): 830-4.
[5] Hsu A L, Tang P F, Jan M H. Analysis of impairments influencing gait velocity and asymmetry of hemiplegic patients after mild to moderate stroke[J]. Arch Phys Med Rehabil, 2003, 84(8): 1185-93.
[6] Bohannon R W, Andrews A W, Smith M B. Rehabilitation goals of patients with hemiplegia[J]. Int J Rehabil Res, 1988, 11(2): 181-3.
[7] 尹傲冉, 倪朝民, 杨 洁, 等. 脑卒中偏瘫患者步态的不对称性与平衡功能的相关性研究[J]. 中华物理医学与康复杂志, 2014,36(3):190-3.
[8] Kim C M, Eng J J. Symmetry in vertical ground reaction force is accompanied by symmetry in temporal but not distance variables of gait in persons with stroke[J]. Gait Posture, 2003, 18(1): 23-8.
[9] Patterson K K, Gage W H, Brooks D, et al. Evaluation of gait symmetry after stroke: a comparison of current methods and recommendations for standardization[J]. Gait Posture, 2010, 31(2): 241-6.
[10]中华神经科学会,中华神经外科学会. 各类脑血管疾病诊断要点[J]. 中华神经科杂志, 1996, 29(6): 379-80.
[11]Séléna L, Betschart M, Aissaoui R, et al. Understanding spatial and temporal gait asymmetries in individuals post stroke[J]. Int J Phys Med Rehabil, 2014, 2: 201.
[12]Jørgensen L, Crabtree N J, Reeve J, et al. Ambulatory level and asymmetrical weight bearing after stroke affects bone loss in the upper and lower part of the femoral neck differently: bone adaptation after decreased mechanical loading[J]. Bone, 2000, 27(5): 701-7.
[13]Zifchock R A, Davis I, Higginson J, et al. The symmetry angle: a novel, robust method of quantifying asymmetry[J]. Gait Posture, 2008, 27(4): 622-7.
[14]Herzog W, Nigg B M, Read L J, et al. Asymmetries in ground reaction force patterns in normal human gait[J]. Med Sci Sports Exerc, 1989, 21(1): 110-4.
[15]Chisholm A E, Perry S D, McIlroy W E. Inter-limb centre of pressure symmetry during gait among stroke survivors[J]. Gait Posture, 2011, 33(2): 238-43.
Explore the best calculation method of symmetry ratio of center of pressure
Liu Liling, Ni Chaomin, Yue Tong, et al
(DeptofRehabilitationMedicine,TheAffiliatedProvincialHospitalofAnhuiMedicalUniversity,Hefei230001)
To explore the best calculation method of the symmetry ratio of center of pressure(COP) during gait among hemiplegic stroke survivors. Thirty-three hemiplegic stroke survivors were selected for gait analysis. Three different calculation methods were used for the symmetry ratios of COP related parameters. The correlations between velocity and symmetry ratios were analyzed. The calculation methods influenced the correlations between velocity and symmetry ratios. In order to reflect the correlation between velocity and asymmetry more objectively, for the parameters during single support phase, the paretic gait parameters could be used as numerator, and during double support phase, the greater value as numerator. When necessary, the best method can be decided according to scatter diagram, or subgroup analysis can be done.
troke; gait disorders; neurologic; center of pressure; velocity; gait asymmetry
安徽省科技厅年度重点科研项目(编号:11070403064)
安徽医科大学附属省立医院康复医学科,合肥 230001
刘丽玲,女,硕士研究生; 倪朝民,男,教授,主任医师,硕士生导师,责任作者,E-mail:nchm@sohu.com
时间:2016-10-12 13:23:00
http://www.cnki.net/kcms/detail/34.1065.R.20161012.1323.035.html
R-32;R 493
A
1000-1492(2016)11-1700-04
10.19405/j.cnki.issn1000-1492.2016.11.035
2016-05-19接收

