基于已知传播模式数目的海杂波抑制方法研究

李雪 郭晓彤 王岳松 李吉宁

(中国电波传播研究所,青岛 266107)



基于已知传播模式数目的海杂波抑制方法研究

李雪 郭晓彤 王岳松 李吉宁

(中国电波传播研究所,青岛 266107)

天波超视距雷达海杂波谱受电离层多模传播影响大幅展宽,需进行杂波抑制才可实现舰船目标检测,利用电离层返回散射探测可获得海杂波谱先验模式数目信息. 针对常用的两种海杂波抑制方法——特征值分解法和循环对消法,仿真分析了传播模式数目识别准确性对海杂波抑制效果的影响. 结果表明:若传播模式数目识别错误,则会造成目标漏检或虚警. 在传播模式数目已知的前提下,利用仿真和试验数据研究了目标与一阶海杂波多普勒相对位置和多普勒分辨率对上述两种方法海杂波抑制效果的影响. 目标与一阶海杂波越接近,海杂波抑制效果越差,当二者相对多普勒位置小于分辨率时,两种方法均失效;多普勒分辨率越低,海杂波抑制效果越差;目标与海杂波越接近,对多普勒频率分辨率要求越高.

天波超视距雷达海杂波谱;传播模式数目;奇异值分解法;循环对消法

DOI 10.13443/j.cjors.2015110902

引 言

天波超视距雷达(Over-The-Horizon Radar, OTHR)利用电离层作为传输介质,可超视距覆盖几千千米范围,实现对弹道导弹、隐身飞机等目标的早期预警,应用前景十分广阔. 而对舰船等低速目标而言,其多普勒频谱与海杂波的一阶谱分量十分接近,目标检测难度较大. 又由于电离层的分层特性,信号回波会出现多模效应,导致杂波谱展宽比较严重,且模式数目不定,进一步加大了低速目标的检测难度[1-2].

为抑制海杂波对目标检测的影响,目前主要有两大类方法:第一类是海杂波循环对消法,将海洋回波的多普勒信号近似认为呈正弦变化,估计一阶海杂波的频率、幅度、相位,在时域上构造对应的正弦信号,与回波相减消去一阶海杂波,凸显目标,文献[3]提出了基于快速傅里叶变换(Fast Fourier Transform,FFT)相位分析的海杂波对消方法,进一步提高了一阶海杂波的频率、相位估计精度,取得了较好效果;第二类是特征值分解法,其中使用频率最高的是奇异值分解(Singular Value Decomposition,SVD)法,对回波信号进行特征值分解,将反映一阶海杂波的奇异值置零,然后重构回波信号,实现一阶海杂波抑制,凸显目标信号[4]. 然而,上述两类方法要求比较准确地估计传播数目,即一阶海杂波谱峰数目,否则不能选择合适的对消次数或置零个数,严重影响海杂波抑制效果,从而导致无法有效实现舰船目标检测. 针对传播模式数目估计问题,文献[5]提出基于先验返回散射探测的传播模式区提取方法,实现了任意距离单元的传播模式数目准确提取.

本文针对常用的两种海杂波抑制方法——SVD法和基于FFT相位分析杂波循环对消法,仿真分析了传播模式数目识别准确性对海杂波抑制效果的影响. 并在假设传播模式数目已知的前提下,利用仿真和试验数据研究了目标与一阶海杂波多普勒相对位置和多普勒分辨率对上述两种方法海杂波抑制效果的影响.

1 海杂波模型

1955年,Crombie提出用谐振散射机理描述高频无线电波与海浪的一阶作用. 根据该理论,海洋表面波可看成一系列正弦信号的叠加. 假设其波长为L,雷达发射的无线电磁波波长为λ,入射角为α,当波长满足Lcosα=λ/2时,各反射点回波的波程差正好为λ的整数倍,此时,回波信号同相相加,产生一阶Bragg散射,且一阶Bragg峰对应的多普勒频率为

(1)

式中: g为重力加速度; α为海浪与雷达照射方向夹角; f0为雷达载频,MHz; ±号为朝向及背离雷达波束的谐振海浪所产生的正负Bragg峰[6]. 谱峰的相对强度反映了引起海浪的表面风风向. 一阶谱峰的强度很大,是海洋回波的主要成分,在高频海洋回波谱中,表现为一对关于零频对称的谱峰,若存在电离层多模传播效应,回波谱中还会存在多对一阶Bragg谱峰. 本文将利用频率为fB的两个正弦信号模拟一阶海杂波,同时通过添加不同的多普勒频移模拟高频雷达多模传播下海洋回波谱.

2 海杂波抑制方法

2.1 奇异值分解法

海杂波可以看成是窄带的时变信号,用时变信号处理技术能进行频率跟踪[7]. 因此,将雷达回波的时域信号构造成Hankel矩阵,对其进行奇异值分解,产生的奇异值与一阶海杂波的频率分量一一对应,通过把对应一阶海杂波的奇异值置零实现海杂波的抑制.

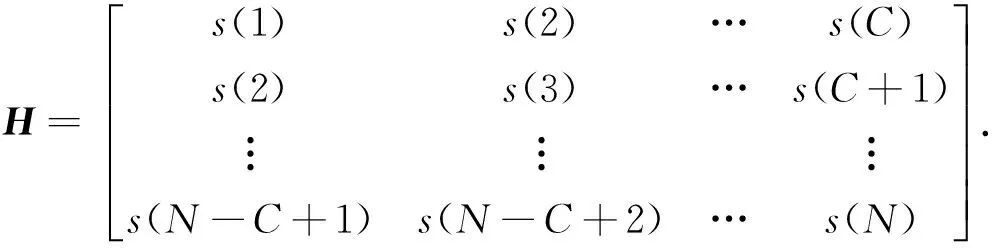
(2)

矩阵H经奇异值分解后表示为

H=USVT.

(3)

式中: S=diag(σ1,σ2,…,σC),σ1≥σ2≥…≥σC≥0是矩阵H的奇异值; U、V为奇异值对应的左、右奇异矢量. 奇异值反映了信号、杂波干扰和噪声的能量集中情况,前r个较大的奇异值依次主要反映大的信号能量,较小的奇异值对应噪声,中间部分则主要对应于二阶海杂波、慢目标及其他杂波. 由于一阶海杂波集中在正负Bragg峰附近,且远高于目标及其他杂波强度,与较大的奇异值对应,因此,将一阶海杂波奇异值置零,重构信号后能较好地消除一阶海杂波,实现舰船目标检测.

2.2 基于FFT相位分析的海杂波循环对消

海杂波循环对消思想是利用FFT找到一阶海杂波的主要分量,通过估计该分量的幅度、频率和初相重构正弦信号,在回波信号中将其减去,循环迭代此过程直到一阶海杂波去除,凸显出目标信号为止. 因此,这种方法要求对正弦信号的幅度、频率、相位的估计非常精确. 但是传统的海杂波对消法频率分辨率低,实际的一阶谱峰对应的频率可能不在离散频率点上,导致估计精度下降,剩余杂波产生扩散.

(4)

式中,T为积累时间. 当Δf超出变化范围[-0.5/T, 0.5/T]时,需要进行

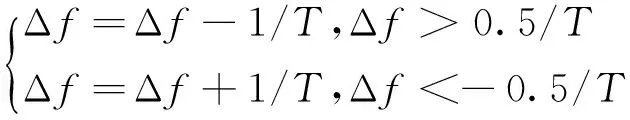
(5)

(6)

φm=φ0+(1-1/N)ΔfTπ.

(7)

3 仿真研究

3.1 传播模式数目识别准确性对海杂波抑制影响研究

假设雷达工作频率为10 MHz,脉冲重复周期为0.2 s,相干积累次数为512,一阶Bragg峰对应的多普勒频率为0.322 6 Hz. 同时假设当前电离层存在E、F两个传播模式,其中E模式引起的相对多普勒频移为0.05 Hz,其回波杂噪比为35 dB,F模式引起的相对多普勒频移为0.07 Hz,其回波杂噪比为30 dB. 目标多普勒位于0.35 Hz,信噪比25 dB,该回波信号如图1黑色线所示. 单从谱图上只能看到一对一阶谱峰,然而该谱峰中包含着E、F两种传播模式下的一阶海杂波和目标,这就存在传播模式数目识别问题.

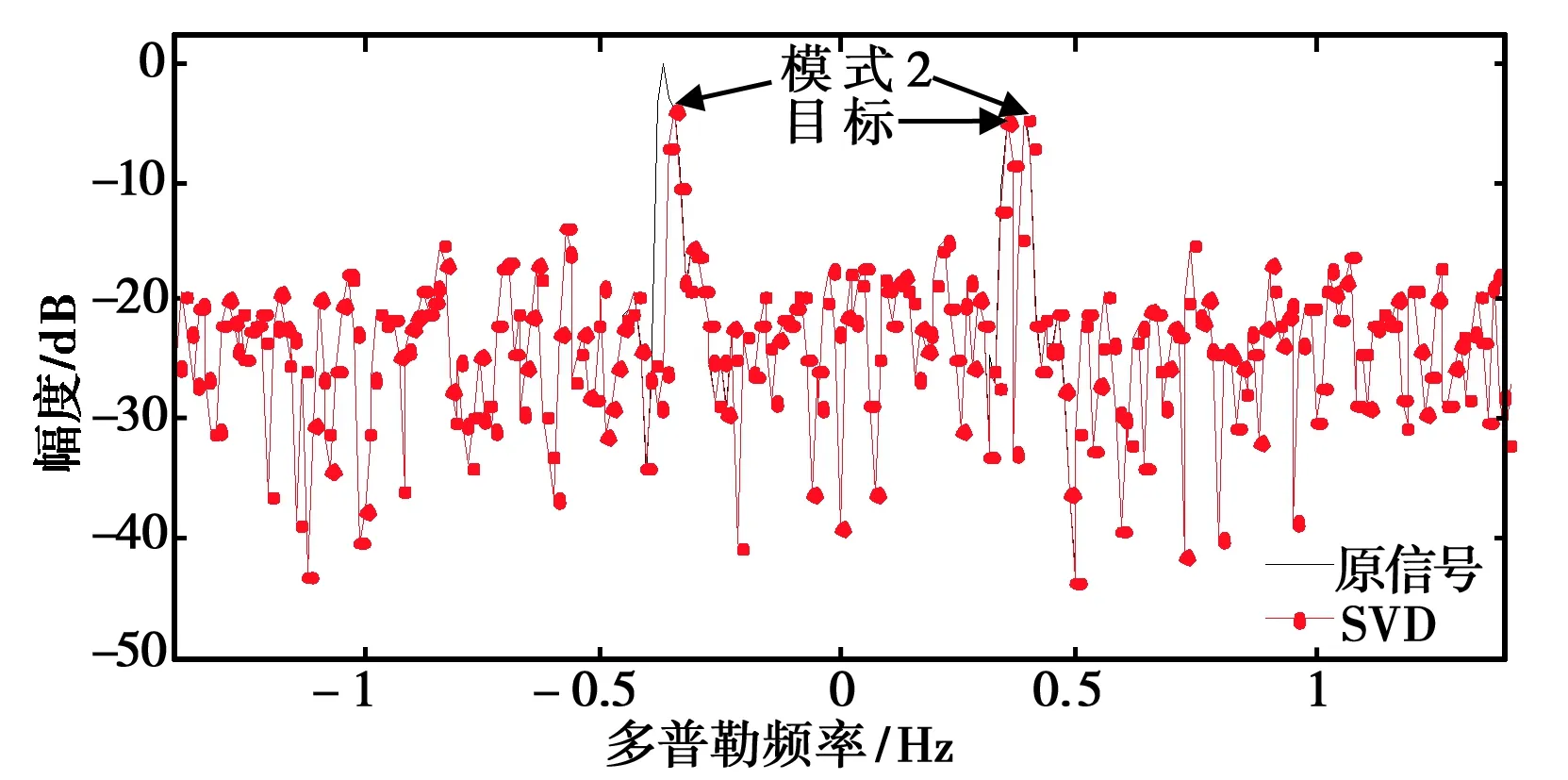
(a) SVD抑制结果

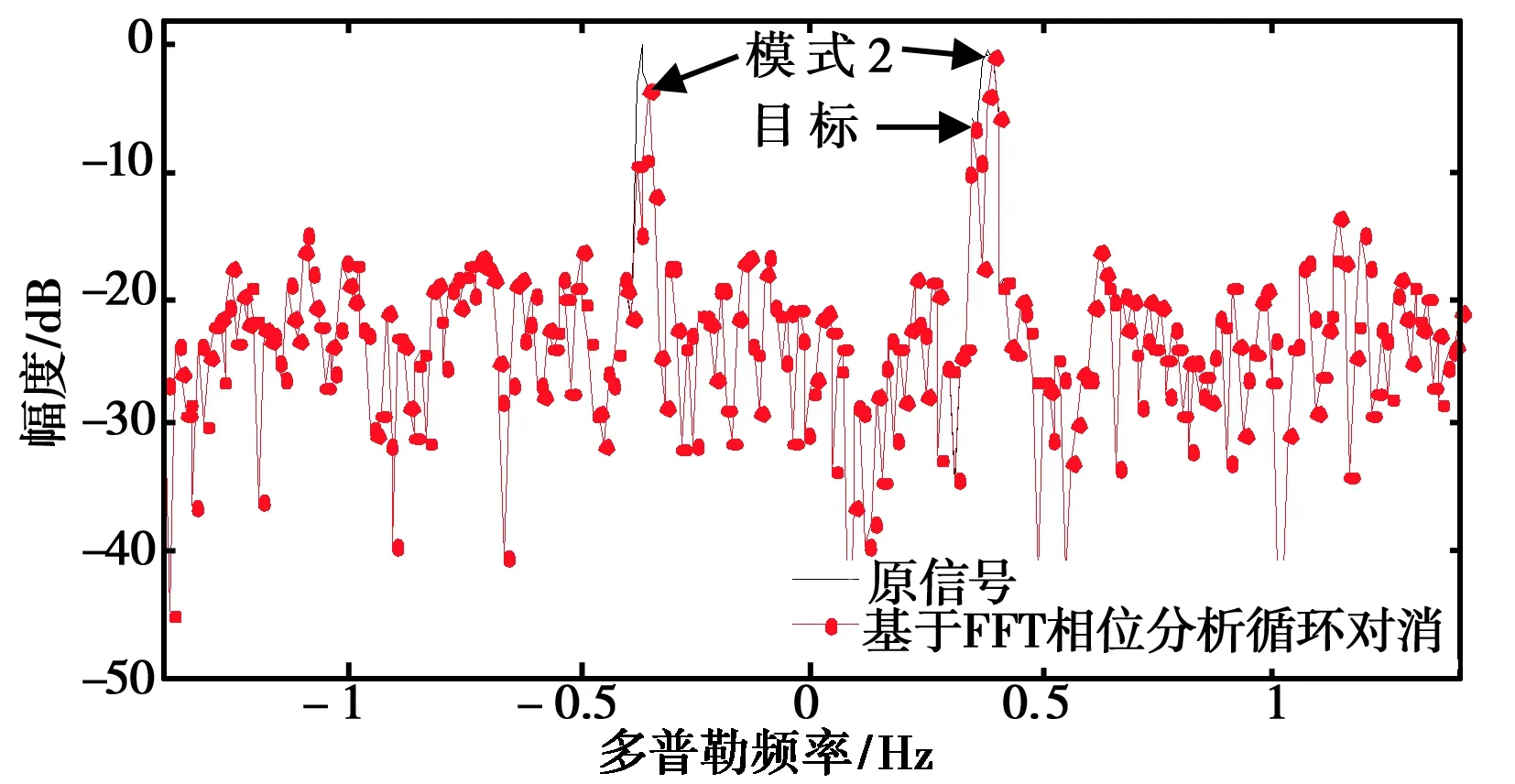
(b) 基于FFT相位分析循环对消抑制结果图1 传播模式数目判少的抑制结果

利用基于SVD抑制海杂波和基于FFT相位分析循环对消两种方法对上述雷达回波信号进行海杂波抑制. 若按照传播模式数目为1对海杂波进行抑制,则只能消除其中一种模式下的一阶海杂波,如图1所示,此时剩余三个较大的谱峰,会均被视为目标,而实际上真实目标只有一个,另外两个均为模式F的一阶谱峰,从而造成虚警. 若按照传播模式数目为3对海杂波进行抑制,则会连目标一并消除,如图2所示,此时会认为没有目标存在,产生漏警. 因此,当传播模式数目识别与真实的传播模式数目不一致时,无法实现有效的目标检测.

若按照传播模式数目为2分别对海杂波进行抑制,则结果如图3所示,E、F模式下的一阶海杂波均被消除,仅凸显出真实目标位置.

通过以上仿真可看出,只有当传播模式数目识别与真实传播模式数目一致时,基于SVD海杂波抑制法和基于FFT相位分析循环对消法才能有效检测出真实目标. 因此,传播模式数目识别的准确性对海杂波抑制效果影响非常大,抑制前必须获得正确的传播模式数目,文献[5]已提出有效方法,利用基于先验返回散射探测的传播模式区提取传播模式数目.

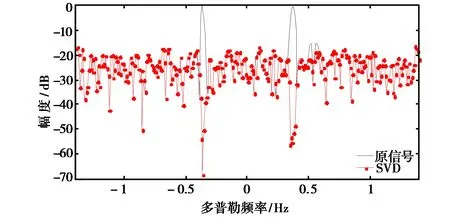
(a) SVD抑制结果

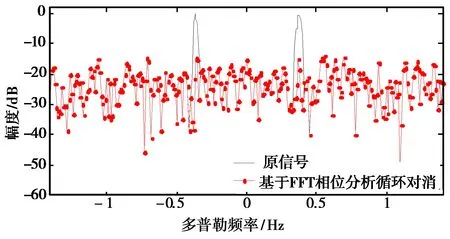
(b) 基于FFT相位分析循环对消抑制结果图2 传播模式数目判多的抑制结果

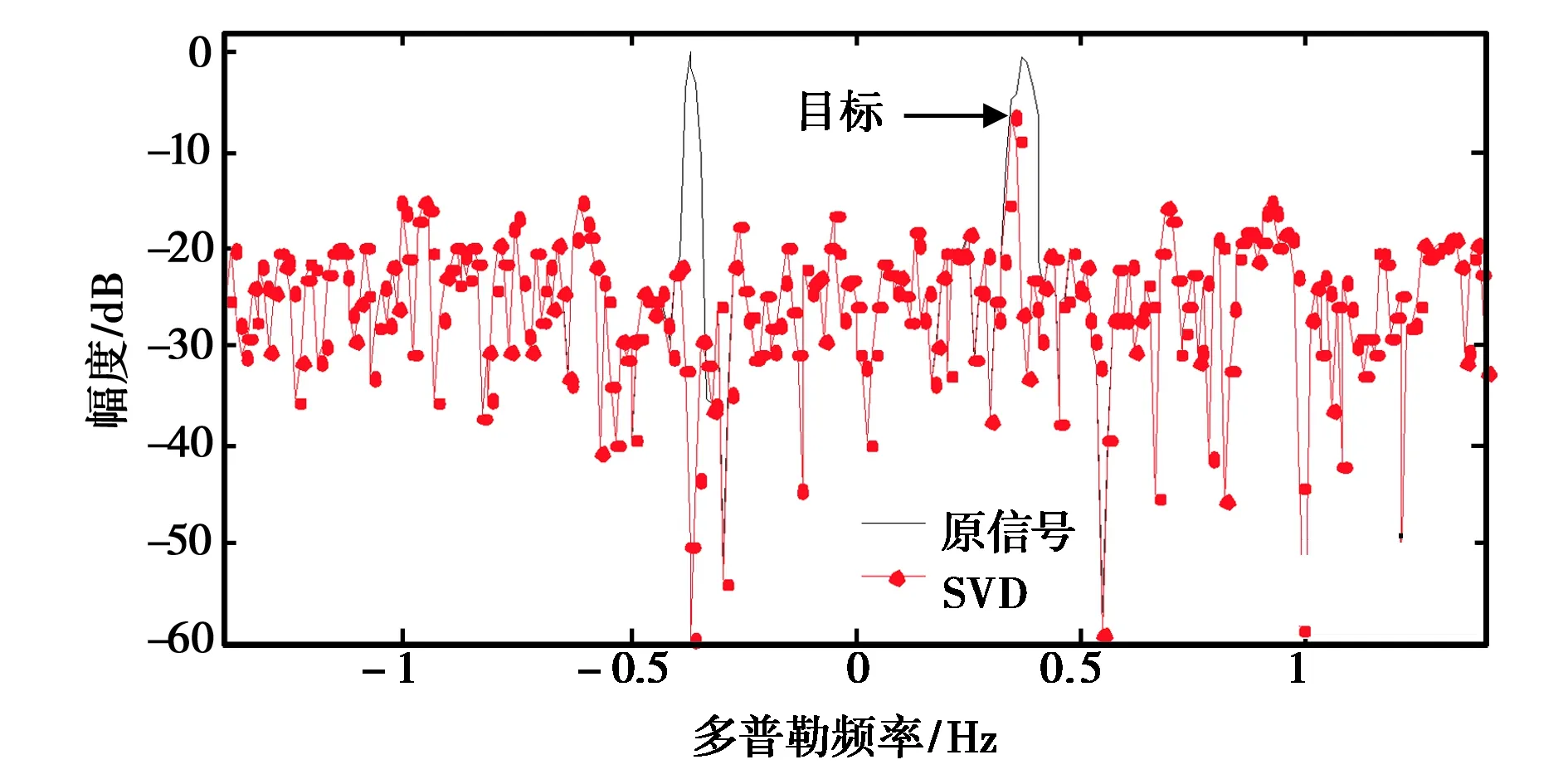
(a) SVD抑制结果

(b) 基于FFT相位分析循环对消抑制结果图3 传播模式数目一致的结果

3.2 目标与海杂波之间的位置关系对抑制效果影响

假设雷达工作频率、脉冲重复周期、相干积累次数、一阶Bragg峰对应的多普勒频率与3.1节仿真条件一致,并假设当前电离层仅存在一个传播模式E,其回波杂噪比为35 dB,目标多普勒频率在[0.29, 0.36] Hz范围内以0.01 Hz步进,信噪比为25 dB.

利用基于SVD抑制海杂波和基于FFT相位分析循环对消两种方法对上述雷达回波信号进行海杂波抑制,以目标与一阶海杂波多普勒之差为相对位置,统计出目标与海杂波相对位置关系对抑制效果影响的曲线图,如图4所示.

从图4可以看出,当相对位置为-0.03 Hz时,两种方法抑制后的信杂比在20 dB左右,随着目标与一阶海杂波相对位置减小,抑制后的信杂比逐渐降低,当目标与海杂波相距小于频率分辨率时,两种方法均不能正确检测出目标,而随着目标与一阶海杂波相对位置增大,抑制后的信杂比再次逐渐升高. 因此,当目标接近一阶海杂波时,两者相对位置越远,海杂波抑制效果越好,且基于FFT相位分析循环对消的抑制效果略好.

3.3 多普勒分辨率对海杂波抑制效果影响

假设雷达工作频率、脉冲重复周期、一阶Bragg峰对应的多普勒频率、传播模式与3.2节仿真条件一致,减少采样点数,使其在[670, 220]范围内以-30递减.

设目标多普勒为0.36 Hz,与海杂波相对位置为0.03 Hz,信噪比25 dB,采用SVD和基于FFT相位分析循环对消法分别进行海杂波抑制,结果如图5(a)所示. 改变目标位置,使其位于0.35 Hz和0.34 Hz处,与海杂波的相对位置为0.02 Hz和0.01 Hz,抑制后信杂比分别如图5(b)、(c)所示.

从图5(a)可以看出,当多普勒频率间隔为0.007 Hz时,抑制后的信杂比为21 dB,当多普勒频率间隔增加到0.022 Hz时,SVD抑制海杂波后的信杂比降到15 dB,基于FFT相位分析循环对消抑制后的信杂比降到16.2 dB. 因此,随着多普勒分辨率下降,两种方法的信杂比都随之降低,相比之下,基于FFT相位分析循环对消的效果较好,图5(b)、图5(c)均能反映出该变化过程.

(b) 目标相对位置0.02 Hz

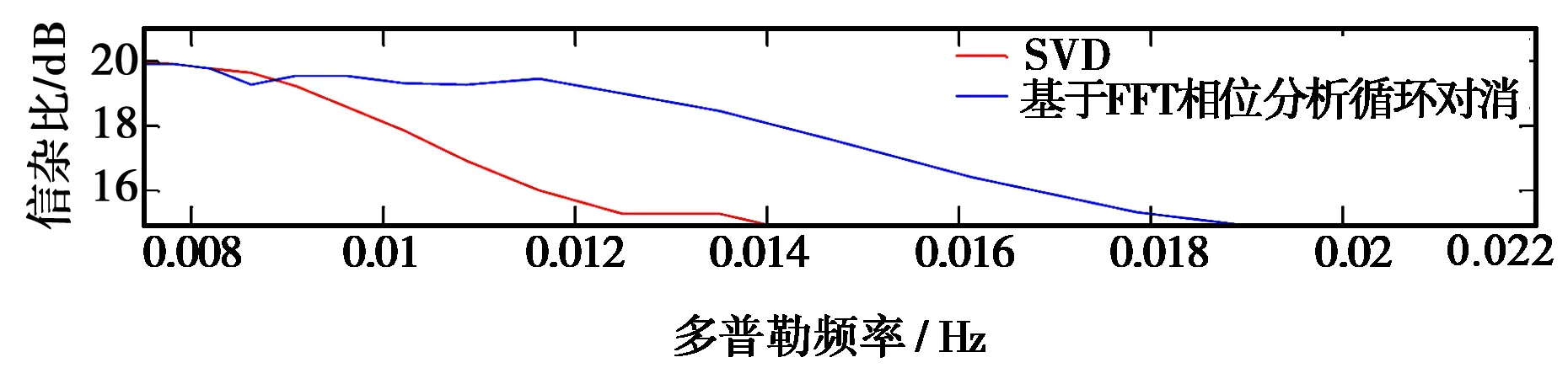
(c) 目标相对位置0.01 Hz图5 随频率分辨率变化的两种方法抑制后的信杂比

对比图5的三幅图可知:当目标与海杂波相对位置为0.03 Hz时,多普勒频率间隔大于0.022 Hz时就无法凸显出真实目标;当目标与海杂波相对位置为0.02 Hz时,频率间隔大于0.018 Hz时SVD法失效,大于0.022 Hz时基于FFT相位分析循环对消法失效;当目标与海杂波相对位置为0.01 Hz时,频率间隔大于0.014 Hz时SVD法失效,大于0.018 Hz时基于FFT相位分析循环对消法失效. 因此,随着目标与海杂波相对位置的减小,需要的多普勒分辨率随之提高.

4 实测数据验证

考虑到OTHR数据来源受限,同时高频窄波束返回散射定频探测数据与OTHR回波数据特性相同,均为双程传播,且均受电离层多模传播影响,因此可利用其进行上述算法验证.

获取2009年4月19日5时14分某高频返回散射探测站定频海杂波回波功率谱,工作频率20.528 MHz,群距离1 550 km,脉冲重复周期0.05 s,相干积累次数256,采样频率80 kHz. 在多普勒频率-0.6 Hz和-0.5 Hz处分别添加目标信号,合成的信号谱如图6、图7黑色线所示. 结合先验返回散射探测的传播模式区提取到传播模式数目为1,两种方法的抑制结果分别如图6、图7红色线所示.

目标位于-0.6 Hz时,SVD抑制后的信杂比为43.249 2 dB,基于FFT相位分析法消除后的信杂比为44.003 0 dB,两种方法抑制效果相近,基于FFT相位分析循环法的效果略优于SVD. 而当目标位于-0.5 Hz时,两种方法均无法实现目标检测. 因此,目标与海杂波越接近,抑制效果越差,与仿真结果一致.

仿真条件不变,仅将相干积累次数减少,依次更改为192和128,两种方法的抑制结果分别如图8、图9所示.

当积累次数为192时,SVD抑制海杂波后的信杂比为41.070 3 dB,基于FFT相位分析法抑制后的信杂比为42.457 5 dB,较积累次数为256,两种方法的抑制效果均下降,但基于FFT相位分析的效

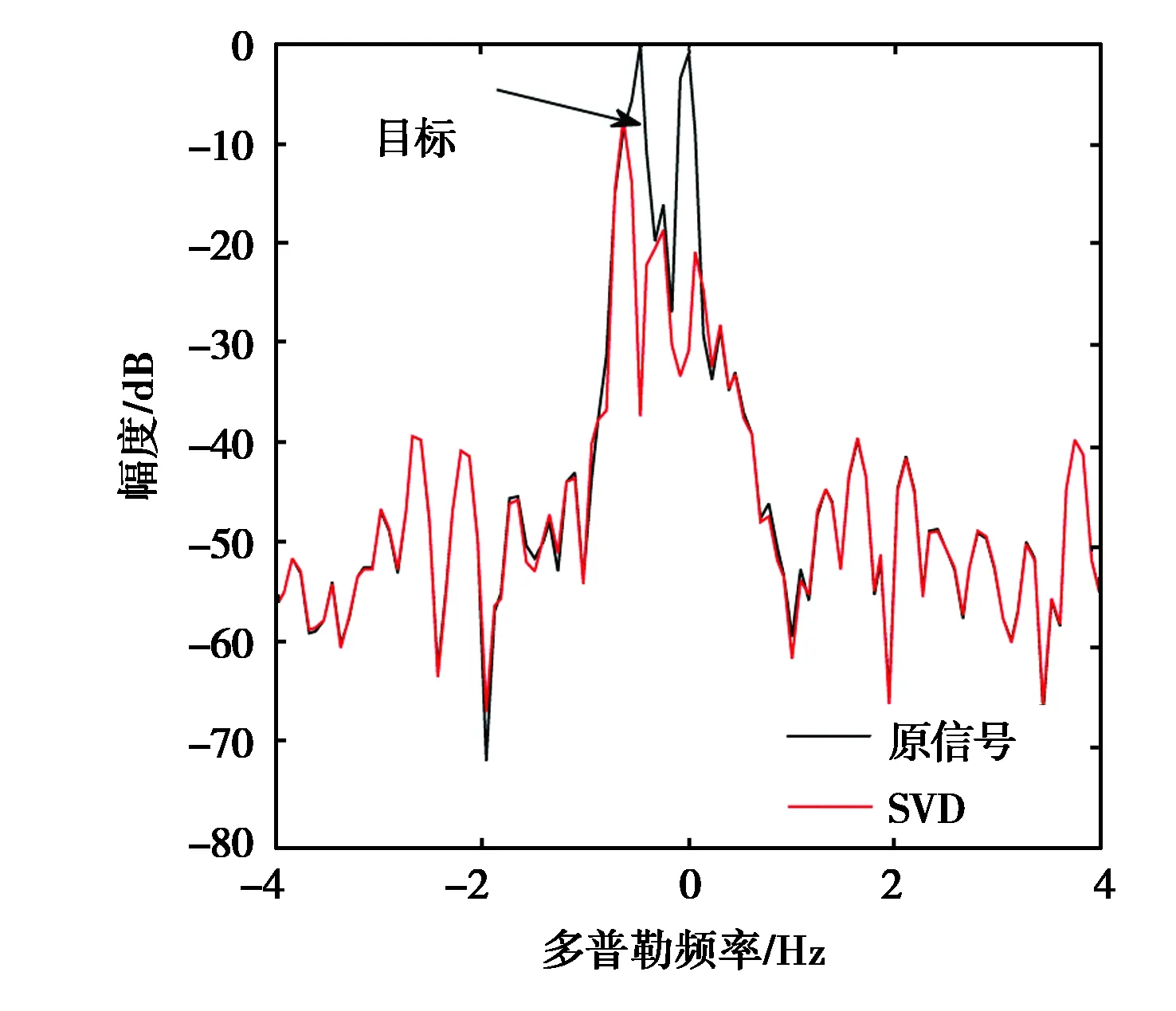
(a) 目标位于-0.6 Hz处

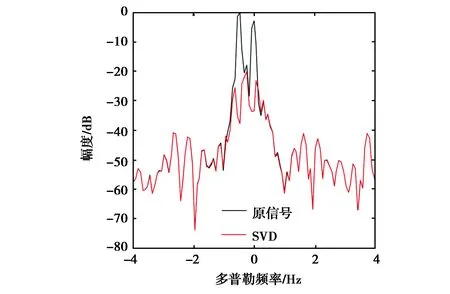
(b) 目标位于-0.5 Hz 处 图6 SVD抑制海杂波(实测数据)

果仍然相对较好. 当积累次数为128时,两种方法均无法正确检测目标. 因此,随着分辨率下降,海杂波抑制效果逐渐变差,同时结合图6、图7可以看出,当目标与海杂波相对位置越近,对多普勒分辨率的要求越高,与仿真结果一致.

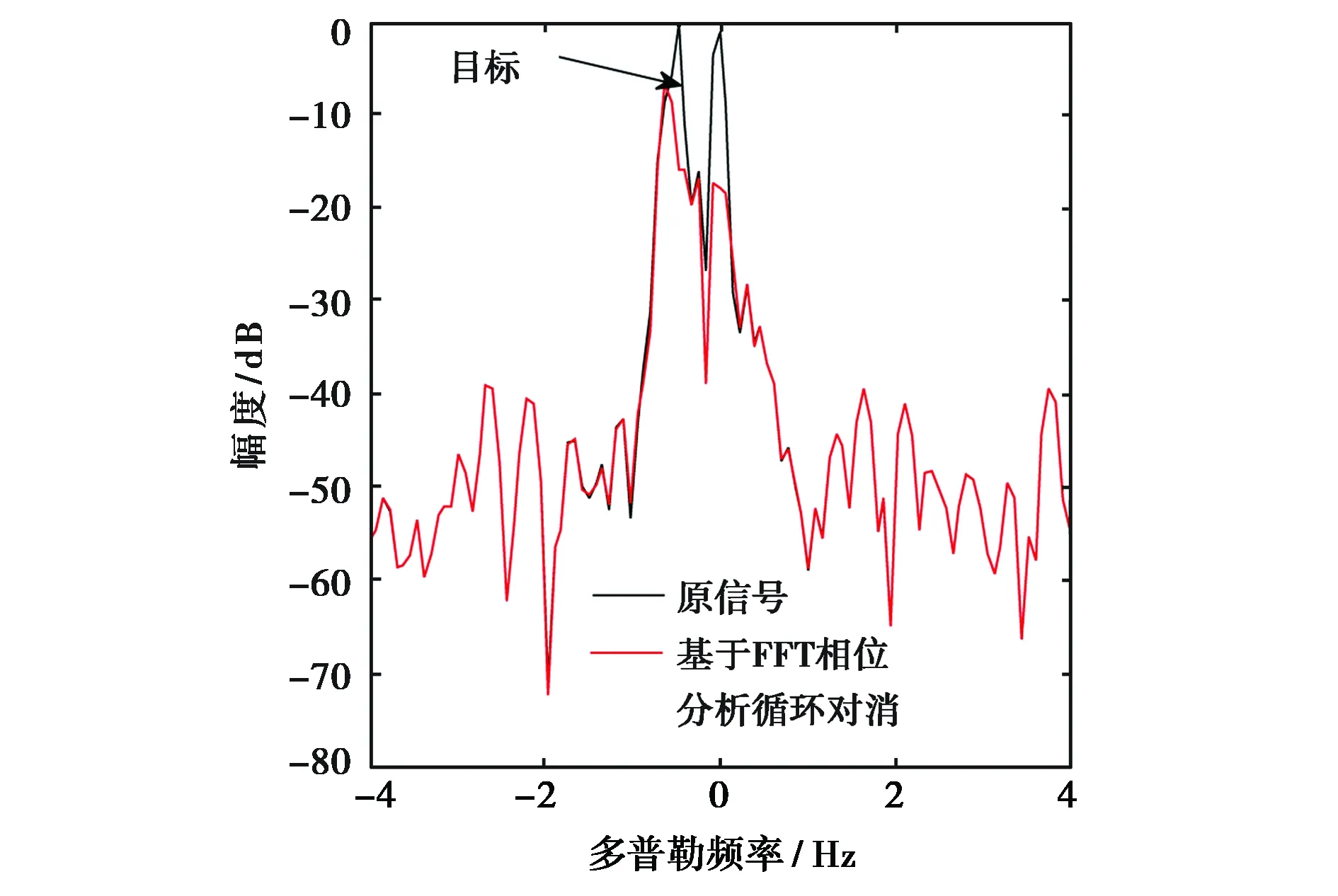
(a) 目标位于-0.6 Hz处

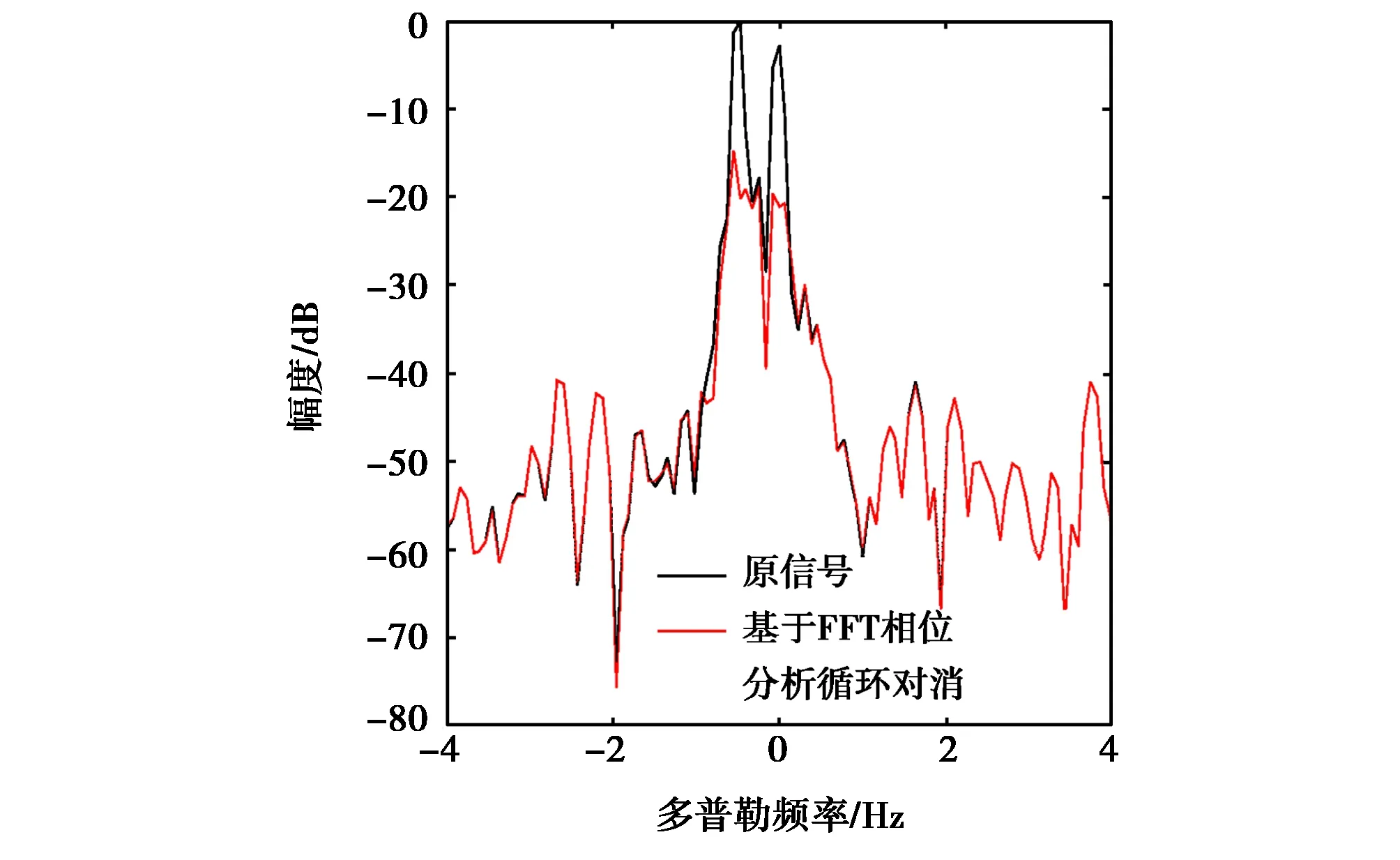
(b) 目标位于-0.5 Hz 处图7 基于FFT相位分析法消除海杂波(实测数据)

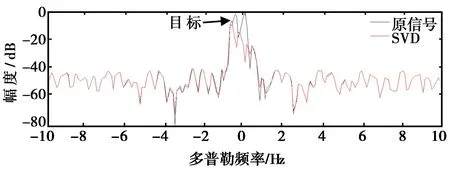
(a) 积累次数192

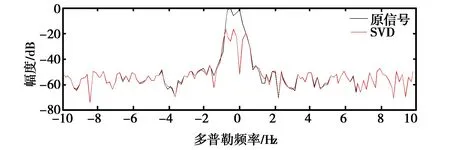
(b) 积累次数128图8 不同分辨率下SVD抑制结果

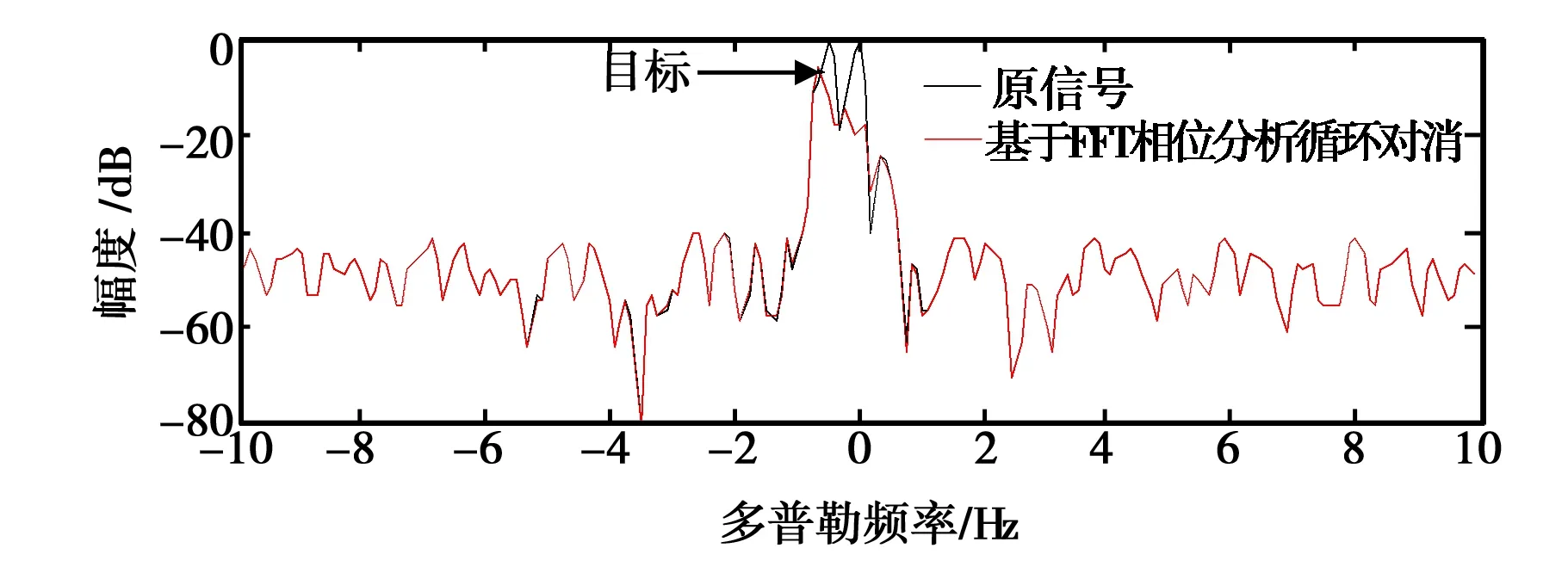
(a) 积累次数192

(b) 积累次数128图9 不同分辨率下基于FFT相位分析抑制结果

5 结 论

本文通过仿真多模效应下奇异值分解法和基于FFT相位分析法抑制海杂波的结果,反映出已知传播模式数目的重要性,并从目标与海杂波相对位置关系和多普勒频率分辨率对海杂波抑制结果的影响两个方面对比分析两种方法的目标检测能力. 经试验验证,目标与海杂波相对位置越近,抑制效果越不好;多普勒频率分辨率越低,抑制效果越不好. 目标与海杂波越接近,对多普勒频率分辨率要求越高. 在同等条件下,基于FFT相位分析法的抑制效果较好.

[1] 周文瑜, 焦培南. 超视距雷达技术[M]. 北京:电子工业出版社, 2008: 224.

[2] 凡俊梅, 焦培南, 肖景明. 海洋杂波对高频雷达检测海面上低速目标的影响[J]. 电波科学学报, 1997, 12(2): 205-210.

FAN J M, JIAO P N, XIAO J M. The sea clutter effect on the low Doppler targets detection by HF radar[J]. Chinese journal of radio science, 1997, 12(2): 205-210.(in Chinese)

[3] 郭欣, 倪晋麟, 刘国岁. 短相干积累条件下天波超视距雷达的舰船检测[J]. 电子与信息学报, 2004,26(4):613-618.

GUO X, NI J L, LIU G S. The ship detection of sky wave over-the-horizon radar with short coherent interaction time[J]. Journal of electronics information technology, 2004, 26(4): 613-618. (in Chinese)

[4] POON M W Y, KHAN R H, LE-NGOC S. A singular value decomposition(SVD) based method for suppressing ocean clutter in high frequency radar[J]. IEEE transactions on signal processing,1993,41(3): 1421-1425.

[5] 李雪, 李吉宁, 冯静, 等. 天波超视距雷达多模传播抑制[J].电波科学学报, 2015, 30(1):57-62.

LI X, LI J N, FENG J, et al. OTHR multi-mode propagation suppression[J]. Chinese journal of radio science, 2015, 30(1): 57-62. (in Chinese)

[6] ANDERSON S J, MAHONEY A R, TURLEY M D E. Applications of superresolution techniques to HF radar sea echo analysis[C]//Proceedings of the Pacific Ocean Remote Sensing Conference, Melbourne, 1994.

[7] KHAN R H. Ocean-clutter model for high frequency radar[J]. IEEE journal of oceanic engineering, 1991,16(2):181-188.

李雪 (1981-),男,黑龙江人,博士,高级工程师,目前主要研究方向为电离层回波信号处理、雷达信号处理、电波传播等.

郭晓彤 (1989-),女,河北人,助理工程师,目前主要研究方向为电离层电波传播、雷达信号处理.

王岳松 (1981-),男,山东人,工程师,目前主要研究方向为计算机算法及应用、大数据分析、模式识别算法以及频率选择方法.

李吉宁 (1982-),男,山东人,工程师,目前主要研究方向为高频雷达信号处理和电波传播.

Sea clutter suppression algorithm based on ionospheric propagation mode number

LI Xue GUO Xiaotong WANG Yuesong LI Jining

(ChinaResearchInstituteofRadioWavePropagation,Qingdao266107,China)

Since the sea clutter spectrum of over-the-horizon radar(OTHR) always has large spreads due to the ionospheric multimode propagation, the clutter suppression needs to be done for detection of ship targets. The information of a priori mode number for the sea clutter spectrum can be acquired via ionospheric backscatter sounding. The effects of the identification for propagation mode number on the suppression of sea clutter are simulated and analyzed based on two common methods of sea clutter suppression, namely, the singular value decomposition (SVD) algorithm and the phase information of Fourier transform algorithm. The results show that target false-alarm or false-dismissal will occur if the identification of propagation mode number is not correct. Furthermore, the influence of the distance between the target and the first-order sea clutter and the Doppler resolution on the sea clutter suppression using the above two methods is studied through both simulated and experimental data with the precondition of known propagation mode number, and consequently two conclusions are obtained. The first conclusion is that the closer the target is to the first-order sea clutter, the worse the suppression of sea clutter operates, and when the distance of the two is within the Doppler resolution range, neither of the two methods works. The second one is that the sea clutter suppression effect is poorer with the lower Doppler resolution, and closer distance between target and clutter will require higher Doppler frequency resolution.

OTHR sea clutter spectrum; propagation mode number; SVD; the phase information of Fourier transform

10.13443/j.cjors.2015110902

2015-11-09

国家自然科学基金青年基金(No.61302006)； 中国电科技术创新基金(JJ-QN-2013-28)

TN011.2

A

1005-0388(2016)04-0700-07

李雪, 郭晓彤, 王岳松, 等. 基于已知传播模式数目的海杂波抑制方法研究[J]. 电波科学学报,2016,31(4):700-705.

LI X, GUO X T, WANG Y S, et al. Sea clutter suppression algorithm based on ionospheric propagation mode number[J]. Chinese journal of radio science,2016,31(4):700-705. (in Chinese). DOI: 10.13443/j.cjors.2015110902

联系人： 郭晓彤 E-mail: xtguo1206@sina.cn