高频地波雷达射频干扰抑制新算法的研究

文必洋 韩金柱 周企豪 李艳

(武汉大学 电子信息学院雷达与信号处理实验室,武汉 430079)



高频地波雷达射频干扰抑制新算法的研究

文必洋 韩金柱 周企豪 李艳

(武汉大学 电子信息学院雷达与信号处理实验室,武汉 430079)

针对高频地波雷达易受到其他设备发射的高频信号干扰的问题,通过分析射频干扰与有效目标信号在雷达回波中的表现形式及其在雷达距离多普勒谱图中出现区域的差异,运用多重信号分类算法估计射频干扰的频率和方位角子空间,利用子空间投影的方法分别在频率和方位角上分解射频干扰信号和有用目标回波信号,之后从原信号中减去射频干扰分量,从而实现射频干扰抑制的目的．仿真结果与实测数据的处理结果都表明:该算法可以有效抑制射频干扰.

高频地波雷达;射频干扰抑制;MUSIC算法;子空间分解

DOI 10.13443/j.cjors.2015091101

引 言

高频地波雷达(High Frequency Surface Wave Radar, HFSWR)利用高频段(3～30 MHz)电磁波可以沿海面或地面绕射的特性实现超视距目标探测和海洋动力学遥感,众所周知有非常多的通讯设备都工作于该频段,非合作设备的发射信号对于雷达来说都是射频干扰,这些干扰将严重降低雷达的目标探测与海洋遥感性能,因此迫切需要寻找一种行之有效的射频干扰抑制方法．

国内外雷达领域的很多学者对不同体制雷达的射频干扰抑制方法做了深入研究,常用的算法有:利用最小均方误差自适应滤波器进行合成孔径雷达数据的射频干扰抑制[1-2],该方法的缺点是步长参数μ选取不当容易造成自适应算法发散,而且对参考信号要求较高;利用射频干扰的距离相关特性进行特征子空间分解[3-5],该方法的缺点是若射频干扰与目标信号(包括海杂波)在距离多普勒谱(Range-Doppler,RD)图中叠加在一起,这种算法就会失去其作用;利用自适应旁瓣对消法抑制射频干扰[6-7],该方法需要一个复杂的天线系统,实现起来比较困难;以及利用自回归(Auto Regressive, AR)模型预测射频干扰然后剔除[8-9]或者利用最小二乘法在时域或距离域进行抑制[6]等很多算法,这些方法的结果都不够理想．

考虑到射频干扰的距离相关性和来波方向固定特点,结合HFSWR的波形体制及数据处理方法,本文提出了新的射频干扰抑制算法:首先利用经典谱估计方法中的多重信号分类(Multiple Signal Classification,MUSIC)算法估计射频干扰的频率子空间与方位角子空间,在这两个参数的限制下基本可以保证射频干扰与目标和海洋回波是分离的,这就为射频干扰的提取创造了条件,之后在频率和方位角的子空间进行空间分解,获得射频干扰分量．

1 射频干扰分析

1.1 数学模型

射频干扰的调制方式有多种,但对HFSWR而言起主要干扰作用的是其载波成分,可以将射频干扰用若干单频信号的组合模型来描述:

(1)

式中: al、fl、φl0分别为第l个干扰信号的幅度、频率、初相位．为便于书写,后面公式中假设只有一个单频干扰．

1.2 表现形式

现代HFSWR常采用线性调频中断连续波体制,通过两次傅里叶变换来获得目标的距离与速度信息,即在快时间维(距离维)作第一次傅里叶变换,在慢时间维(多普勒维)作第二次傅里叶变换[10-11]．雷达本振信号为(不考虑中断门控影响):

0≤ti≤T.

(2)

式中: T为扫频周期; ti为一个周期的内部时间; n代表第n个扫频周期．将射频干扰与雷达本振信号混频之后通过低通滤波保留差频部分,经过同相(I)和正交(Q)双通道采样转化为解析信号,低通滤波结果如下:

Sn= abexp[j2πflnT+jφl0]

(3)

按照文献[10]的采样方法获得二维数据矩阵,列数表示相干积累的周期个数,行数表示一个扫频周期内的采样点数．第一次傅里叶变换在每列上进行,固定n值,对应于ti作变换,结果为

Fn(f) =abexp(j2πflnT+jφl0)

(4)

式中,fl0=fl-f0是频率差．式(4)积分部分是Fresnel积分,频率占据整个接收机频带范围,表明每个距离单元都有值．

(a) 实测数据的RD图

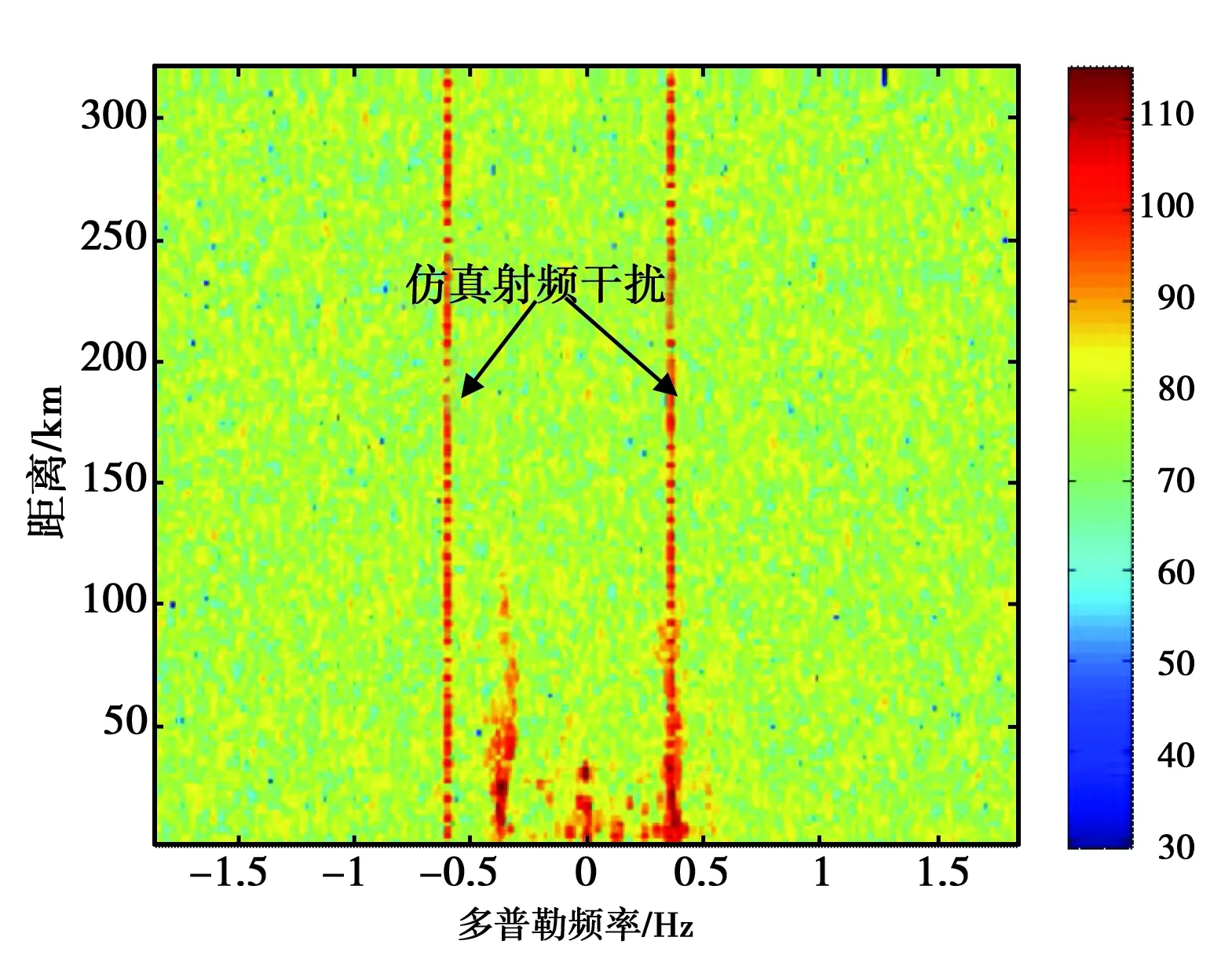
(b) 叠加了仿真射频干扰的RD图图1 射频干扰表现形式

固定距离单元,即固定f值,可以发现每个相干积累周期在该距离元的幅度相同,相位在相邻两个扫频周期有2πflT的变化,这个相位变化在所有距离单元上都是相同的．第二次傅里叶变换就是针对n作变换,所有距离单元产生的谱峰在相同位置,呈现带状结构,如图1所示．

图1(a)是一幅实测数据的RD图,含有射频干扰．图1(b)是一幅实测无干扰但叠加了仿真射频干扰的RD图,结果分析中会给出这两幅图的射频干扰抑制结果．正如理论分析,射频干扰体现在所有距离单元,且频点位置相同,幅度不同．当射频干扰与海洋回波和目标点叠加在一起时如图1(a),常用算法很难将其分离,本文算法却能很好地解决这个问题．本文挑选了几场没有射频干扰的数据,然后加入图1(b)仿真的两个射频干扰,对比原数据与仿真处理结果以验证算法的正确性．

2 算法分析

2.1 MUSIC算法估计子空间

经典的参数估计方法有MUSIC算法、子空间旋转不变技术(Estimating Signal Parmeters via Rotational Invariance Techniques,ESPRIT)算法,本文应用MUSIC[12]算法估计频率与方位角子空间．

MUSIC算法的理论分析这里不作描述,仅就子空间的获取稍作说明．MUSIC算法利用的是噪声子空间,通过最优化搜索与噪声子空间垂直的导向矢量来确定频率或方位角,本文不需要知道具体的参数信息,直接获得大特征值对应的特征向量作为射频干扰的频率和方位角子空间．

频率子空间估计国内外已有人做过相关研究,这里不再赘述,可参考文献[3,5]．方位角子空间估计也是利用远距离元回波数据,但有几点需要注意:首先常用MUSIC算法是在时域进行的, HFSWR通常是在频域处理数据,由于天线阵元之间的相位差在时域与频域保持不变,所以完全可以将MUSIC算法推广到频域,只是相关矩阵的构造方法要做相应改变(构造方法下文会有详细说明)．其次方位角子空间估计与分解过程都在第二次快速傅里叶变换(Fast Fourier Transform,FFT)之后进行．因为MUSIC算法要求信源数小于天线阵元个数,而射频干扰信源数具有不确定性,在两次FFT变换之后射频干扰在多普勒维被分开,在射频干扰不是相干信号源的假设下可以认为每个谱点都是单到达角,这样理论上两根天线就可以估角,取最大特征值对应的特征向量作为方位角子空间UN．通常射频干扰的载频都不同,所以上述假设是合理的．

2.2 子空间分解

射频干扰可以进行空间分解[13]的基础就在于上面得到的子空间UN．

假设矩阵X是n×m维矩阵,X的列空间C(X)就是X的列向量的线性组合所张成的空间:

C(X)=a1x1+a2x2+…+amxm．

(5)

若矩阵的列线性无关,则所有列就称为该空间的一组基,取其中某几列所张成的空间就称为C(X)的子空间．若C(X)的两个子空间互为正交补,子空间基向量为c1、c2,且z=z1+z2∈C(X),z1∈c1,z2∈c2．定义正交投影算子满足

Pz=z1,(I-P)z=z2,

(6)

则针对c1的正交投影算子为

(7)

(8)

信号在UN中的射频干扰分量为

(9)

目标信号分量为

(10)

本文的思想就是首先获得射频干扰的频率和方位角子空间,然后将回波数据在子空间投影得到射频干扰分量,最后在原信号中减去该分量以达到抑制效果．

3 算法实现

本文通过对仿真数据的处理流程来说明射频干扰抑制的具体实施过程．

3.1 仿真条件

本文仿真了两个单频射频干扰加入到无干扰雷达数据中,仿真参数基于武汉大学电子信息学院雷达与信号处理实验室设计的OSMAR-SD HFSWR,具体参数如表1所示．

仿真天线是三元单极子线阵,阵元间距λ/2．快时间维做过傅里叶变换之后有128个有效距离元,两个射频干扰的方位角设置为30°和-45°,每根天线叠加这两个干扰时附加上对应的时间延迟为

(11)

添加之后第一根天线的RD图如图1(b)所示．

表1 OSMAR-SD雷达参数

通过观察图1可以发现,有效回波信号大都集中在40个距离单元以内,较远距离元的信号都是接收机的内部噪声,这是因为雷达设计的最大探测距离都要大于实际探测距离,以避免出现距离模糊．通常雷达数据处理中远距离信号都是直接丢掉,从数据利用率的角度来讲这无疑是浪费．这一区域的数据只含有射频干扰与噪声的信息,这为获得射频干扰子空间提供了理想条件．

3.2 算法过程

本文算法可分为两部分,首先进行频率子空间分解,然后进行方位角子空间分解．

3.2.1 频率子空间分解

分解过程参考文献[3,5],在第一次FFT之后进行．图2展示了直接从原数据中减去该分解结果之后第4和第10个距离单元的多普勒谱与添加干扰之前这两个距离元的多普勒谱的对比．可以发现,位置1的射频干扰抑制效果很好,但位置2处的射频干扰被抑制的同时该位置的海洋回波一阶峰也被削弱了25 dB左右,削弱后与噪声强度相差无几,这对提取该位置的风浪流参数与目标参数影响是非常巨大的．

由此可以看到该方法的不足之处:仅在射频干扰与目标信号(包括海杂波)不重叠的情况下能取得较理想的抑制结果,但是当它们重叠的时候会将目标信号也当作射频干扰抑制掉,这样射频干扰抑制就变得没有意义,因为我们的目的就是要凸显出被射频干扰覆盖掉的目标,无目标区域可以不做检测处理．

(a) 第10距离单元的多普勒谱

(b) 第4距离单元的多普勒谱图2 频率子空间分解抑制结果

这种不足在实测数据的处理中体现的尤为明显:实际的射频干扰不会如仿真这般只存在于某几个多普勒频点,而是展宽很严重,只采用频率子空间分解抑制方法会导致展宽区域的信号都被削弱,因此需要对该方法的结果做进一步分解．

常用射频干扰抑制算法只考虑了射频干扰的时域特性,而在阵列雷达信号处理中回波的空域信息是非常重要的参数,本文正是利用方位角信息的差异做后续的射频干扰与目标信号的分离,也就是方位角子空间分解,这也是本文的创新点所在．可以认为出现与射频干扰同频同方位角的目标信号的小概率事件不会发生．

3.2.2 方位角子空间分解

上面得到的频率分量与原雷达数据矩阵维数相同,对其做慢时间维的第二次FFT变换得到Sf,之后就是对Sf做方位角子空间分解．

方位角子空间估计与分解过程如下:

1) 雷达采样数据做过两次FFT变换之后判断受射频干扰影响的多普勒频点,记录这些频点位置,假设有m个．

2) 选择一个射频干扰多普勒频点(本文从第1个开始),取频点位置的远距离元大信噪比数据构造相关矩阵R1．图3所示是其中一根天线数据选择示意图,灰色区域为射频干扰频点,椭圆包围部分即是待选数据．本文取的距离元范围是60～128,进一步筛选出3根天线信噪比都大于10 dB的数据,筛选之后通常剩余30～50个距离元的数据．大信噪比的数据以及30个快拍数基本能保证MUSIC估角准确性较高．利用最大似然法估计R1,有

(12)

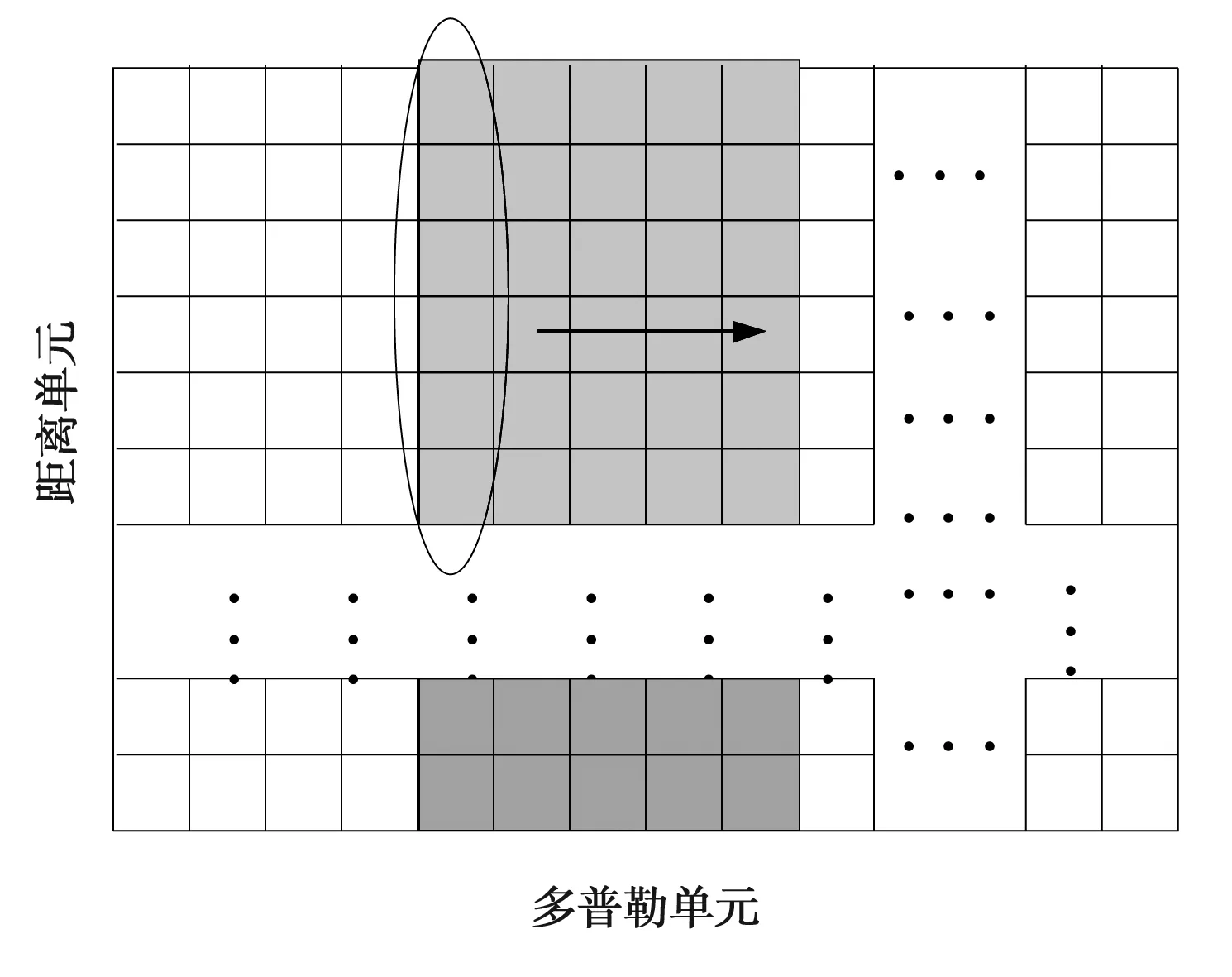
图3 数据选择示意图

4) 取出Sf中3根天线第1个距离单元对应于该多普勒频点的数据组成3×1矩阵x1,1,将其乘以投

影算子得到射频干扰分量s1,1:

(13)

s1,1也是3×1矩阵,代表了第1距离元该多普勒频点处的射频干扰值．用s1,1替代掉Sf中对应位置的频率子空间分解结果,即用s1,1替代x1,1．

5) 重复步骤4)分解Sf中该频点处第2个距离元的数据x1,2,得到s1,2,直到该频点处128个距离元全部分解完成(也可以只分解近距离元有效回波区域的数据),得到s1,1～s1,128．

6) 选择下一个射频干扰多普勒频点,重复步骤2)～5),直到步骤1)中记录的所有多普勒频点的射频干扰方位角子空间估计与分解完成,最后得到射频干扰分量的数据矩阵SRFI,SRFI与频率子空间分解结果Sf相比只在射频干扰的多普勒频点做了进一步分解,其余位置保持不变.

7) 最后用混合了海杂波、目标和噪声的雷达回波数据做两次FFT之后的结果Smix减去射频干扰分量SRFI以达到抑制射频干扰的目的:

ST=Smix-SRFI.

(14)

同样对比本文算法射频干扰抑制结果多普勒谱与添加干扰前多普勒谱,如图4,选择的仍是第4和第10个距离单元,可以发现这两者吻合得非常好,除开噪声不说,在所有的峰值处完全重合．对比图2,位置1处的射频干扰位于噪底中,本文算法优势不能明显体现;位置2处的射频干扰位于海洋回波一阶峰中,本文算法在未削弱一阶峰强度的情况下成功将射频干扰抑制掉,算法优势得以体现．说明经过频率和方位角子空间分解之后射频干扰被完美分离出来．

(a) 第10距离单元的多普勒谱

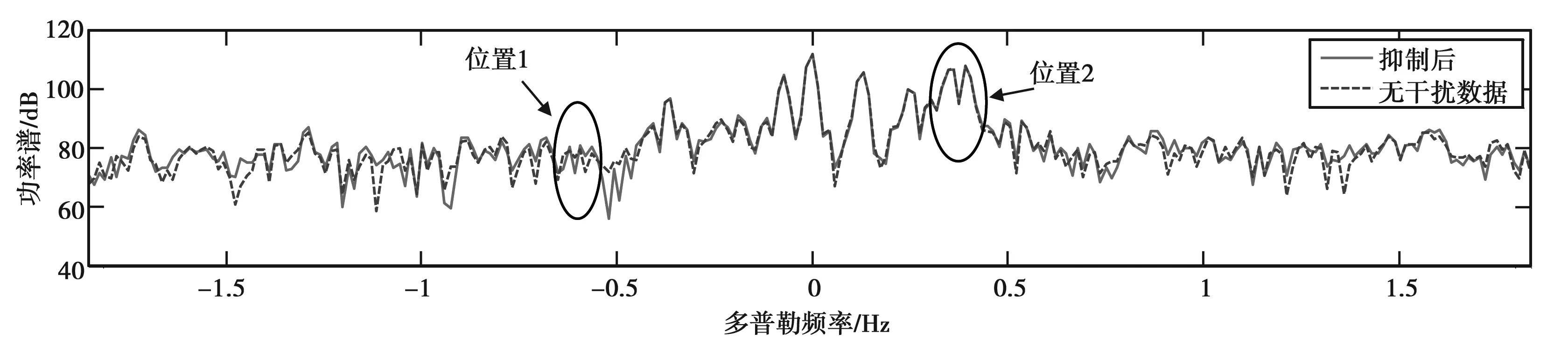
(b) 第4距离单元的多普勒谱图4 本文算法抑制结果

4 算法性能分析

4.1 本文算法抑制结果

由上面的仿真结果可以证明本文算法是射频干扰抑制的有效算法,但是仿真毕竟有其局限性,算法的实际适用性还要靠实测数据的处理结果来证明．图5和图6分别给出了对应图1实测和仿真数据的射频干扰抑制结果,示出的都是第1根天线的RD图及部分距离元的多普勒谱．

对比图5与图1(a),标注的3个区域的射频干扰都被成功抑制掉,负的一阶峰凸显出来,可以较准确地提取该区域的风、浪、流信息,图5(b)示出的是第10个距离元的多普勒谱抑制前后对比．对比图6与图1(b),仿真的两处射频干扰被成功抑制掉,与此同时与射频干扰重叠的正的一阶峰得以完美保留,图6(b)示出的是第10个距离元的多普勒谱抑制前后对比．

综上,本文算法可以有效抑制掉射频干扰同时不损伤被覆盖掉的目标信号．

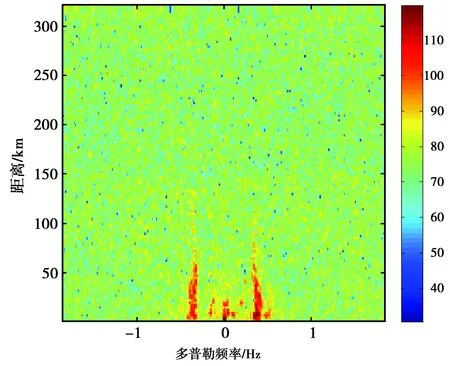
(a) 抑制后RD图

(b) 第10距离元的多普勒谱图5 实测数据抑制结果

(a) 抑制后RD图

(b) 第10距离元的多普勒谱图6 仿真数据抑制结果

4.2 本文算法的局限

通过对大量实测数据的分析发现HFSWR中的射频干扰形式多种多样:有的只出现几个扫频周期的时间,其余时间或是射频干扰没有被发射或是频率不在雷达带宽内;有些呈现斜带状等．当然出现最多的就是上文分析的这种形式．所以文中的级联分解方法并不是对所有形式的射频干扰都适用,比如出现时间极短的强干扰就无法估计其频率,但又不能忽略它对目标检测的影响．

虽然很多形式的射频干扰无法估计其频率,但它的方位角信息一定可以通过阵列信号获得,这样我们可以抛弃频率子空间分解只做方位角子空间分解,只是参与估计方位角的快拍数据要针对不同的射频干扰形式做相应的改变．本文只是提出了该算法,后续还要进一步改善其应用范围．

5 结 论

本文总结了常用射频干扰抑制算法的优缺点,在深入研究MUSIC算法和子空间投影理论的基础上提出了一种新的射频干扰抑制方法,该方法运用MUSIC算法估计频率子空间和方位角子空间,然后利用空间投影进行分解,获得纯粹的射频干扰分量．本文提出的频率与方位角子空间级联分解对大多数的射频干扰形式适用,其余形式的射频干扰可以只做方位角子空间分解,视需要而定．仿真与实测数据的处理结果表明该算法可以有效抑制射频干扰．其它信号分离应用也可借鉴该算法,关键是要获得待处理信号的子空间．

[1] LORD R T, INGGS M R. Approaches to RF interference suppression for VHF/UHF synthetic aperture radar[C]//Proceedings of the 1998 South African Symposium on Communications and Signal Processing. 1998. COMSIG'98. IEEE, 1998: 95-100.

[2] LORD R T. Radio frequency interference suppression applied to synthetic aperture radar data[C]//27th General Assembly of International Union of Radio Science, URSI, 2005.

[3] ZHOU H, WEN B, WU S. Dense radio frequency interference suppression in HF radar[J]. IEEe signal processing letters, 2005, 12(5): 361-364.

[4] 邓巍, 文必洋, 周浩. 基于特征分解的高频地波雷达抗射频干扰研究[J]. 电波科学学报, 2004, 19(5): 565-568.

DENG W, WEN B Y, ZHOU H. Radio frequency interference suppression research in HF surface wave radar based on eigen decomposition[J]. Chinese journal of radio science, 2004, 19(5): 565-568. (in Chinese).

[5] WANG W, WYATT L R. Radio frequency interference cancellation for sea-state remote sensing by high-frequency radar[J]. IET radar, sonar & navigation, 2011, 5(4): 405-415.

[6] 吴敏. 高频地波雷达干扰与杂波抑制方法的研究[D]. 武汉: 武汉大学, 2011.

WU M. Research on interference and clutter suppression methods in HF surface wave radar[D]. Wuhan: Wuhan University, 2011. (in Chinese)

[7] WAN X R, KE H Y, WEN B Y. Adaptive cochannel interference suppression based on subarrays for HFSWR[J]. IEEE signal processing letters, 2005, 12(2): 162-165.

[8] 许瑜昀, 文必洋, 吴雄斌，等. 基于短时傅立叶变换的高频地波雷达射频干扰抑制[J]. 武汉大学学报: 理学版, 2004, 50(5): 645-648.

XU Y Y, WEN B Y, WU X B, et al. Radio frequency interference suppression in HF surface wave radar based on short-time Fourier transform[J]. Journal of Wuhan University: natural science, 2004,50(5):645-648.(in Chinese)

[9] ZHOU H, WEN B Y, WU S C, et al. Radio frequency interference suppression in HF radars[J]. Electronics letters, 2003, 39(12): 925-927.

[10]RICHARDS M A. 雷达信号处理基础[M]. 邢孟道, 王彤, 等译. 北京: 电子工业出版社, 2010: 86-115.

[11]BARRICK D E. FM/CW radar signals and digital processing[R]. National Oceanic and Atmospheric Administration Boulder Co Wave Propagation Lab, 1973.

[12]王永良, 陈辉, 彭应宁, 万群. 空间谱估计理论与算法[M]. 北京: 清华大学出版社, 2004: 18-136.

[13]GILBERT S. Introduction to linear algebra[M]. USA: Wellesley - Cambridge Press, 2009: 121-239.

[14]权太范, 李健巍. 高频雷达抑制冲击干扰的研究与实验[J]. 电子学报, 1999, 27(12): 23-25.

QUAN T F, LI J W. Research and experiment of assault and interference in HF radar[J]. Journal of Electronics, 1999, 27(12): 23-25.(in Chinese)

[15]STOICA P, NEHORAI A. Comparative performance study of element-space and beam-space MUSIC estimators[J]. Circuits, systems and signal processing, 1991, 10(3): 285-292.

[16]LIPA B J, BARRICK D E. FMCW Signal Processing[J]. FMCW signal processing report for Mirage Systems, 1980.

[17]SCHMIDT R O. Multiple emitter location and signal parameter estimation[J]. IEEE transactions on antennas and propagation, 1986, 34(3): 276-280.

[18]LAKE J L, YEARY M, CURTIS C D. Adaptive radio frequency interference mitigation techniques at the National Weather Radar Testbed: first results[C]//IEEE Radar Conference. Cincinnati, OH, May 19-23, 2014: 0840-0845.

[19]ZHOU H, WEN B Y. Radio frequency interference suppression in small-aperture high-frequency radars[J]. IEEE geoscience and remote sensing letters, 2012, 9(4): 788-792.

文必洋 (1963-),男,湖北人,武汉大学电子信息学院教授、博士生导师,主要从事高频地波雷达及信号处理方面的研究．

韩金柱 (1992-),男,河南人,武汉大学电路与系统硕士研究生,从事雷达信号处理研究．

周企豪 (1992-),男,江西人,武汉大学电路与系统硕士研究生,从事雷达信号处理研究．

李艳 (1991-),女,新疆人,武汉大学电路与系统硕士研究生,从事雷达信号处理研究．

New radio frequency interference suppression algorithm in high frequency surface wave radar

WEN Biyang HAN Jinzhu ZHOU Qihao LI Yan

(RadarAndSignalProcessingLaboratory,SchoolofElectronicInformation,WuhanUniversity,Wuhan430079,China)

In order to solve the problem that radio frequency interference(RFI) deteriorate the performance of high frequency surface wave radar (HFSWR) significantly, this paper analyzes the difference of characteristic in radar echoes and range-Doppler(RD) figure between RFI and target signals, estimates the frequency and DOA reference to MUSIC algorithm and uses subspace projection methods to decompose RFI signals and useful target echo signals on DOA and frequency, then subtracts radio frequency interference components from the original signals in order to achieve the RFI suppression. We can conclude that the algorithm can effectively suppress RFI by analyzing simulation results and measured data processing results.

HFSWR; RFI; MUSIC algorithm; subspace projection

10.13443/j.cjors.2015091101

2015-09-11

国家自然科学基金(61371063); 国家重大科学仪器设备开发专项(2013YQ160793)

TN958

A

1005-0388(2016)04-0639-08

文必洋, 韩金柱, 周企豪, 等. 高频地波雷达射频干扰抑制新算法的研究[J]. 电波科学学报,2016,31(4):639-646.

WEN B Y, HAN J Z, ZHOU Q H, et al. New radio frequency interference suppression algorithm in high frequency surface wave radar [J]. Chinese journal of radio science,2016,31(4):639-646. (in Chinese). DOI: 10.13443/j.cjors.2015091101

联系人： 韩金柱 E-mail: 2010301200008@whu.edu.cn