电离层闪烁对GNSS信号影响的相位屏仿真方法
刘钝 於晓 冯健 甄卫民
(中国电波传播研究所,青岛 266107)
电离层闪烁对GNSS信号影响的相位屏仿真方法
刘钝 於晓 冯健 甄卫民
(中国电波传播研究所,青岛 266107)
建立了利用相位屏模型实现的全球导航卫星系统(Global Navigation Satellite System,GNSS)闪烁仿真方法.仿真包括随机相位屏的产生和抛物波方程求解.相位屏产生中,通过将零均值的Gauss白噪声通过特定滤波器(根据闪烁功率谱密度函数设计)的方法产生二维随机相位分布;抛物波方程求解中,通过分步法求解抛物波方程获得接收机处的卫星信号复振幅.上述过程考虑了信号倾斜传播路径、不均匀体特征参量等因素,这些因素可由实测数据估计获得.利用中国低纬地区典型闪烁事件期间的GNSS观测数据提取闪烁相关参量,并用于闪烁仿真.从信号强度时间序列、幅度相位统计特性、谱特征等多个方面,对仿真和实测结果进行比较.结果表明,建立的GNSS信号闪烁仿真方法可以有效复现电离层闪烁影响下的GNSS信号,仿真信号符合理论变化规律,且与实测数据结果具有一致性. 由此表明了建立的GNSS信号闪烁仿真方法的有效性.
电离层闪烁;不均匀体;相位屏;抛物波方程;全球定位系统;仿真
DOI 10.13443/j.cjors.2015083102
引 言
电离层闪烁是影响卫星导航、对地观测(星载合成孔径雷达(Synthetic Aperture Radar,SAR)等系统的重要因素.为实现上述系统中对电离层闪烁影响的分析评估,需建立电离层闪烁模型,模拟生成闪烁影响下的信号形式,并结合系统性能模型,开展电离层闪烁影响的分析研究工作[1-5].
电离层闪烁模型主要包括电离层不均匀体模型和信号传播模型两部分[5-6].电离层不均匀体模型是对造成电离层闪烁的不均匀体特性进行建模,包括不均匀体高度、厚度、强度以及谱指数等特征参量.信号传播模型一般采用相位屏方法实现,这是因为相位屏理论一方面是解释闪烁现象的理论模型之一,另一方面,广泛的试验分析工作验证了相位屏仿真结果与实测结果具有较好的一致性[7-12].不均匀体模型将在其他文章中介绍,本文重点针对电离层闪烁对GNSS信号影响的相位屏仿真实现方法开展研究.
基于相位屏的电离层闪烁分析方法在早期的卫星信标监测电离层闪烁试验中获得验证[7,9].随后,相位屏方法广泛应用于雷达、卫星导航等系统的电离层影响效应分析中.GNSS的出现为电离层闪烁监测提供了一种可广泛应用的手段,但利用GNSS信号进行电离层闪烁监测与早期利用低轨卫星信标监测电离层闪烁存在不同.低轨信标观测中,由于低轨卫星速度很快,相应的信号电离层穿刺点的速度为每秒几千米.在低纬地区,电离层不均匀体的漂移速度一般认为可以达到100 m/s,因此对于低轨卫星信标的电离层闪烁仿真分析而言,可以只考虑电离层穿刺点速度而忽略电离层不均匀体的漂移速度[11].对GNSS而言,卫星一般为中轨道(Middle Earth Orbit,MEO)卫星,信号电离层穿刺点的速度一般为几百米至千米量级,对于北斗系统中广泛使用的倾斜地球同步轨道(Inclined Geo-Synchronous Orbits,IGSO)和静止轨道(Geostationary Earth Orbit,GEO)卫星而言,其信号电离层穿刺点的运动速度与不均匀体的漂移速度量级相当甚至更低,因此在将相位屏方法用于GNSS系统的影响分析和仿真时,必须考虑这种差别.为此,应考虑建立GNSS电离层闪烁观测与分析研究中所需的相位屏实现方法,并结合实际数据,分析验证相位屏方法的有效性.
针对上述问题,本文建立了基于相位屏生成和分步法求解抛物波方程的电离层闪烁仿真方法,并利用中国低纬地区GNSS电离层闪烁观测数据进行仿真方法的实现和验证,结果表明了建立的GNSS信号电离层闪烁仿真方法的有效性.
1 抛物波方程的分步求解
在传播介质不规则性的时间变化与电波信号周期相比较慢,以及不规则体特征尺度远大于波长两个假设下,不规则层内电场矢量的波动方程可以用标量波动方程代替[12-13]:
(1)
式中: E(r)为用相位复矢量表示的电场分量; k=2π/λ为信号波数, λ为信号波长; n为折射指数.式(1)中省略了时间依赖关系exp(iωt).进一步地,将波场E表示为复振幅U(r)的方程:
E(r)=U(r)exp(ik·r).
(2)
引入如图1所示的坐标系,X,Y,Z轴方向分别指向地磁北、地磁东和垂直向下,原点位于信号与电离层的穿刺点处.L为不规则体层厚度.在该坐标系下,传播波矢量为
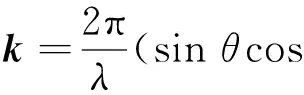
(3)
将式(2)和式(3)带入式(1),可得随机介质波传播的抛物波方程(Parabolic Wave Equation, PWE):
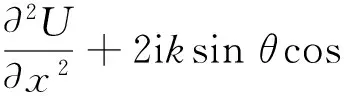
2k2ΔnU=0.
(4)
式中,Δn为不规则体变化引起的折射指数波动变化.在薄相屏近似下,利用分步法可以对式(4)进行求解.
相位屏理论中,将不规则层所起的作用看作一个位于z=0的薄屏,波穿过不规则屏后,只有相位发生变化.因此,穿过相位屏后的复振幅信号为
U(ρ,0+)=U(ρ,0)eiφ(ρ).
(5)
式中: U(ρ,0)为入射到相位屏上的波信号; φ(ρ)为相位屏引起的入射波相位改变量,
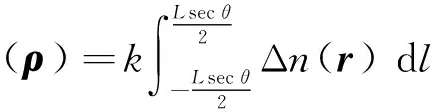
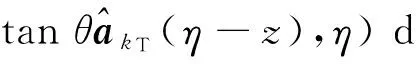
(6)
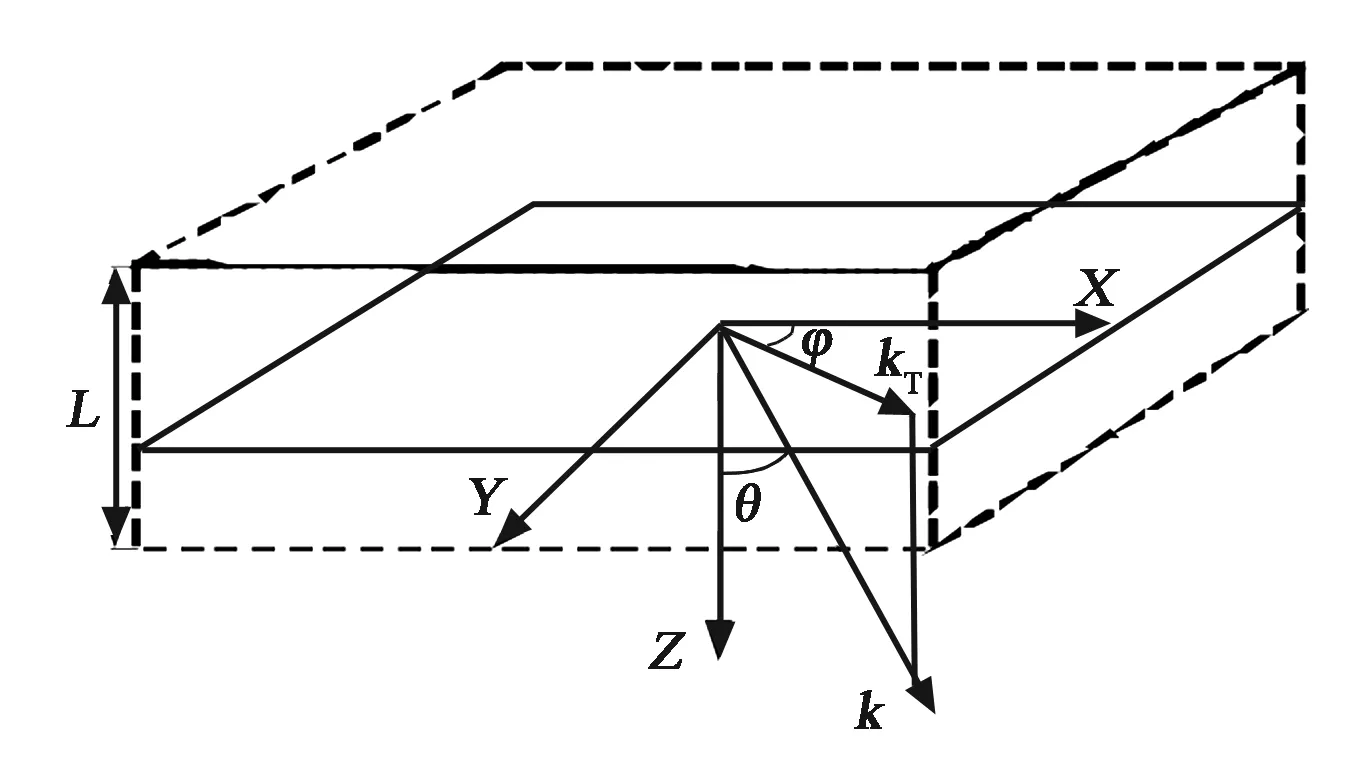
图1 相位屏分析仿真中的坐标系统
从相位屏出射的波按在自由空间传播方式传播至地面接收机天线.对于自由空间传播的波方程,可以采用横向傅里叶变换方法对式(4)进行求解(自由空间传播时Δn为0).
复振幅U(ρ,z)的横向傅里叶变换为
(7)
式中,κ为横向傅里叶波数.到达地面接收机天线的信号复振幅解为
(8)
2 相位屏产生
由第§1可以看出,为实现分步法求解复振幅抛物波方程,需产生满足一定要求的相位屏随机相位分布.Rino和Knepp在其工作中分别介绍过不同的相位屏生成算法[10-11,14].这里采用Rino实现的方法.
复振幅信号穿过相位屏后,引起的信号相位变化满足如下的相位功率谱密度(Power Spectral Density,PSD)函数形式:
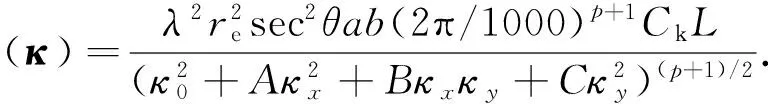
(9)
式中: κ0=2π/L0,L0是电离层不均匀体外尺度; p为相位谱指数; a, b为沿着和垂直于不均匀体主轴的轴比率; κx, κy为横向波数在X,Y轴方向的分量. A,B,C为与传播几何参数(θ, φ),及地磁倾角ψ有关的参数,具体定义可参见文献[8]; CkL为文献[15]中引入的用于描述不规则体强度的参量,CkL与扰动强度Cs、不规则层厚度L,以及谱指数的关系如下:
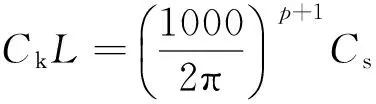
(10)
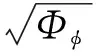
3 闪烁影响下的GNSS信号仿真
为利用相位屏方法实现闪烁影响下的GNSS信号仿真,首先选择典型电离层闪烁事件;对闪烁事件进行分析,提取闪烁相关参量,包括闪烁指数、谱指数、谱强度、漂移速度、CkL,以及信号传播的几何参数等;由闪烁相关参数,利用相位屏产生方法,仿真生成卫星信号穿刺点处相位屏上的相位变化;按分步法求解抛物波方程,获得地面接收机处GNSS信号强度的变化,并进行分析.
图2给出了一次典型电离层闪烁事件的观测结果,观测地点为海口地区,观测时间2014年9月13日,观测信号为北斗系统1号星(PRN1)的B1信号(1 561.098 MHz).北斗系统1号星为GEO卫星,接收机观测仰角为48°,这个仰角可以保证卫星信号受到尽可能少的多径影响.
可以看到,接收的PRN 1卫星信号在北京时间20:30至20:40期间没有受到闪烁影响,信号强度保持平稳状态(GEO卫星相对地球静止,观测仰角相对固定,不存在信号强度随观测仰角的变化).在20:40以后,卫星信号受到闪烁影响,并且影响强度逐渐加强,在20:55左右,卫星信号跟踪中断.选择20:50至20:53期间的闪烁数据进行分析,此时,闪烁为中等强度闪烁(以幅度闪烁指数大于0.3作为中等强度闪烁的判决门限).对上述4分钟内的原始观测数据按每分钟一段进行闪烁指数计算、谱分析及相应的闪烁参数估计,获得的结果见表1.可以看出,这4分钟期间的闪烁为中等强度闪烁,闪烁指数S4为0.3或略大.
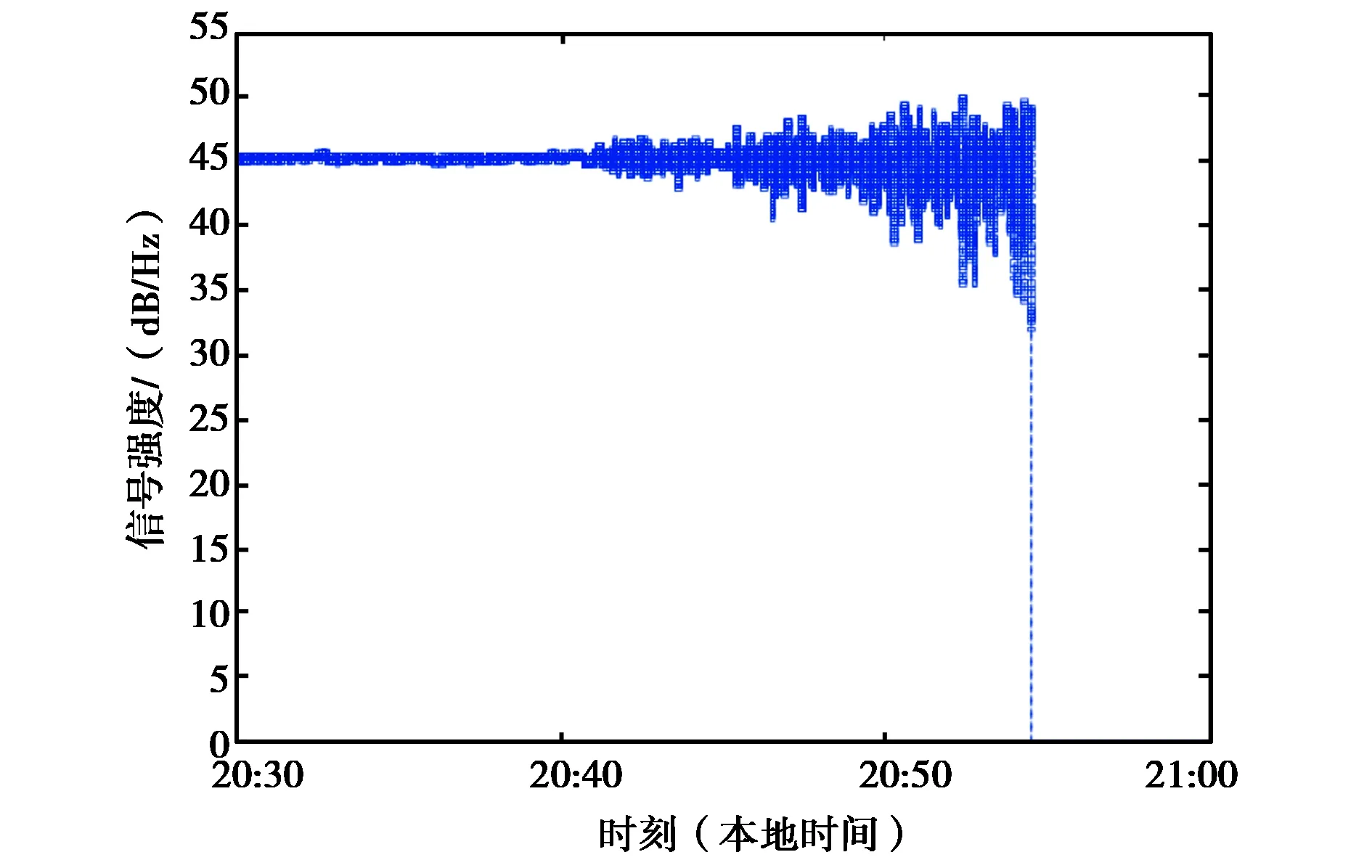
图2 实测的北斗B1信号在电离层闪烁期间的变化(海口地区2014年9月13日)
表1 从原始观测数据中估计的电离层闪烁参量
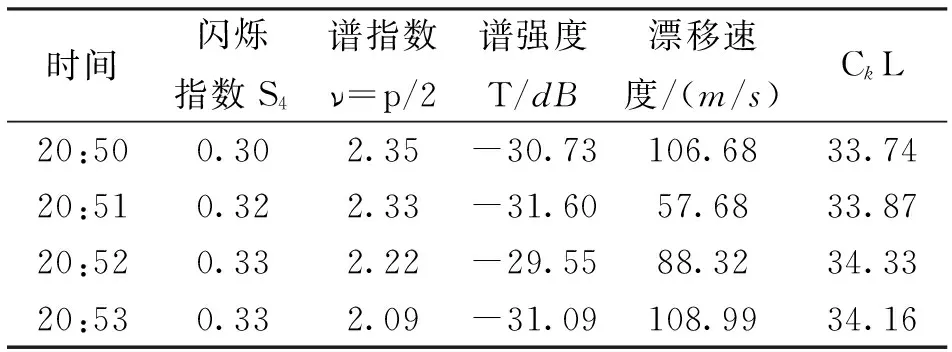
时间闪烁指数S4谱指数ν=p/2谱强度T/dB漂移速度/(m/s)CkL20:500.302.35-30.73106.6833.7420:510.322.33-31.6057.6833.8720:520.332.22-29.5588.3234.3320:530.332.09-31.09108.9934.16
将估计的闪烁谱指数、闪烁强度(CkL)等参量用于§2中介绍的相位屏产生方法,生成位于卫星信号电离层穿刺点处(取350 km高度)模拟相位屏上的相位分布.相位屏仿真中,不均匀体轴比a、b分别取为10和1[16].获得仿真产生的随机相位分布以后,按§1中的分步法求解抛物波方程,获得地面接收机处北斗PRN1卫星信号强度的变化.
图3给出了仿真获得的地面接收平面上卫星信号强度的空间变化分布.尽管GEO卫星信号的电离层穿刺点静止不动,但由于不均匀体的漂移,卫星信号从电离层不均匀体中划过,其在地面的投影如图中蓝色直线所示,红星表示划过路径的起点.
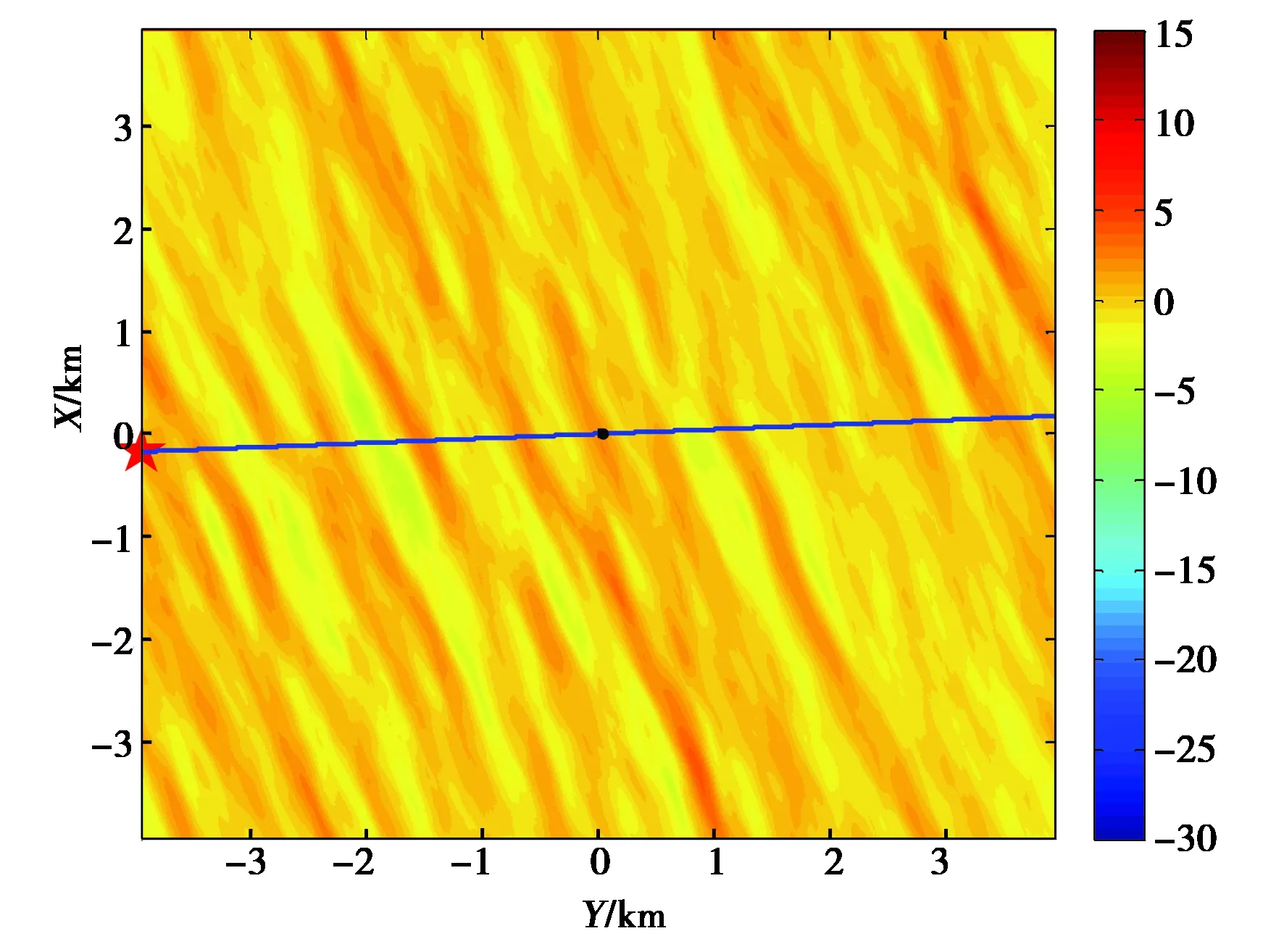
图3 仿真获得的闪烁影响下GNSS信号强度变化
在“冻结场”假设下,可以将电离层不均匀体造成的接收信号强度空间变化转换为信号强度的时间变化,得到信号强度的时间变化序列[10].图4(b)给出了按上述方法获得的接收机处闪烁引起的信号强度时间变化序列.作为比较,同时列出了从20:50至20:53期间原始观测数据中截取的一段信号强度实测结果(图4(a)).
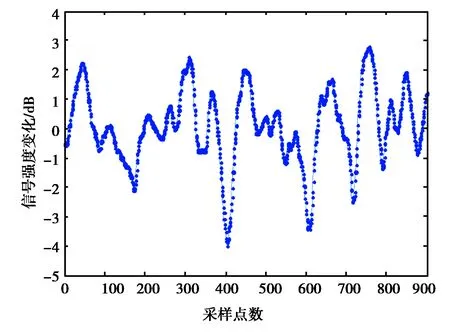
(a) 实测值
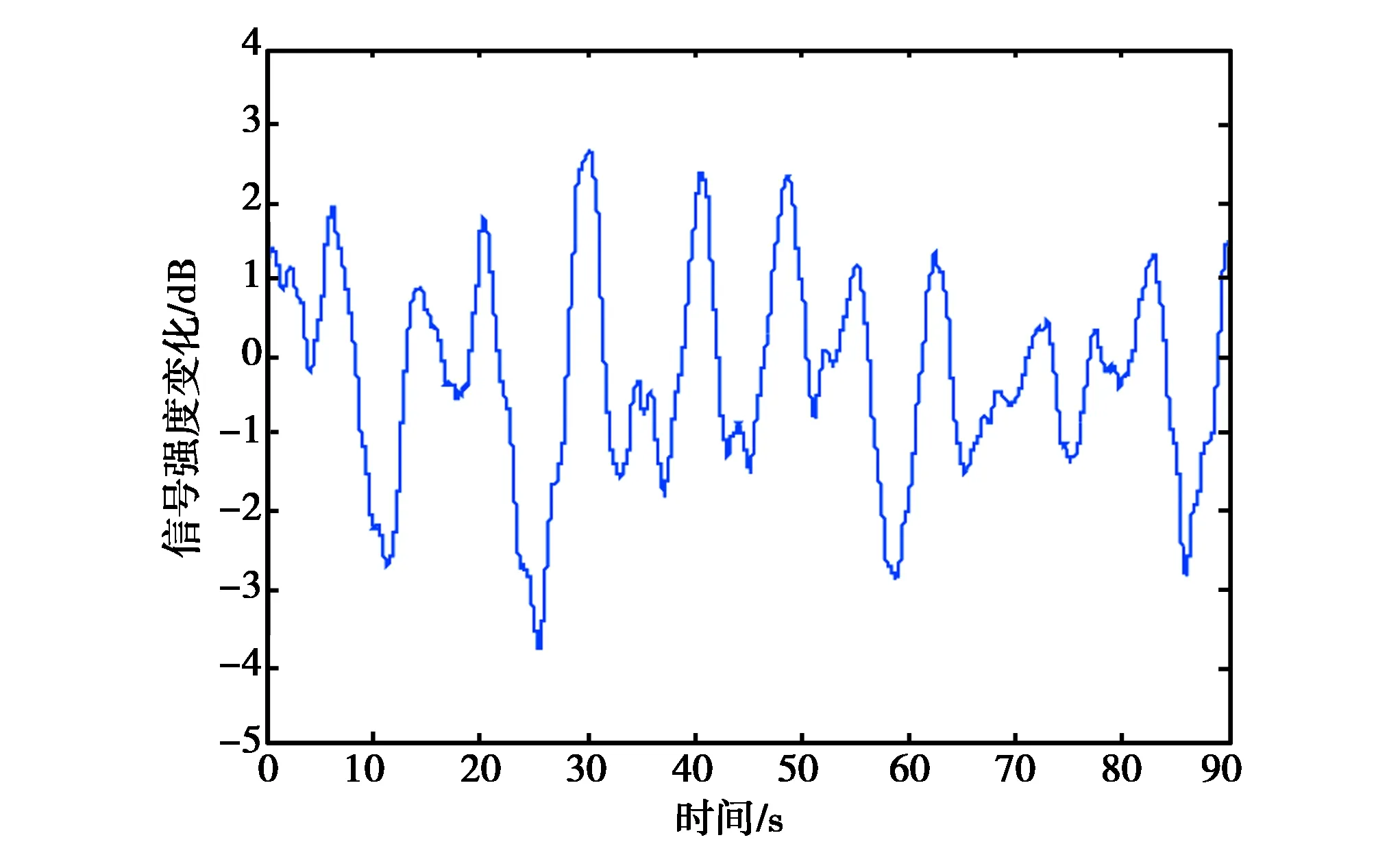
(b) 仿真值图4 电离层闪烁影响下的GNSS信号强度时间变化序列
4 分析与讨论
对相位屏方法仿真获得的闪烁影响下GNSS卫星信号强度变化进行分析,并与实际测量数据结果进行比较,分析相位屏仿真方法的有效性.
4.1 信号强度时间序列
图4给出实测和仿真的闪烁影响下卫星信号强度变化时间序列.闪烁对卫星信号的影响表现为信号强度的快衰落变化.从图中可以看出,实测数据与仿真数据表现出相似的衰落幅度和衰落深度变化.
4.2 信号强度变化的统计特性
由电离层闪烁理论可知,电离层闪烁引起的信号强度变化符合Nakagami分布[10,12]:
(11)
式中: I为信号强度; m为Nakagami分布参数,且与幅度闪烁指数S4存在关系
(12)
对实测的闪烁影响下北斗信号强度起伏数据进行统计分析,并与理论上的统计模型(Nakagami)进行比较,Nakagami模型中所需参数m由实测数据计算的幅度闪烁指数S4获得,实测数据计算的S4为0.3.对相位屏仿真的信号强度起伏数据进行同样的分析,其中利用仿真数据计算的S4为0.29.图5分别给出了实测数据与仿真数据的比较结果.可以看出:
1) 无论是实测数据还是仿真数据,其分布均符合相应的Nakagami分布.
2) 仿真数据计算的幅度闪烁指数S4(0.29)与实测数据的计算结果(0.3)基本相等.
由此表明,仿真的闪烁影响下的卫星信号幅度变化特性与实际信号变化具有一致性.
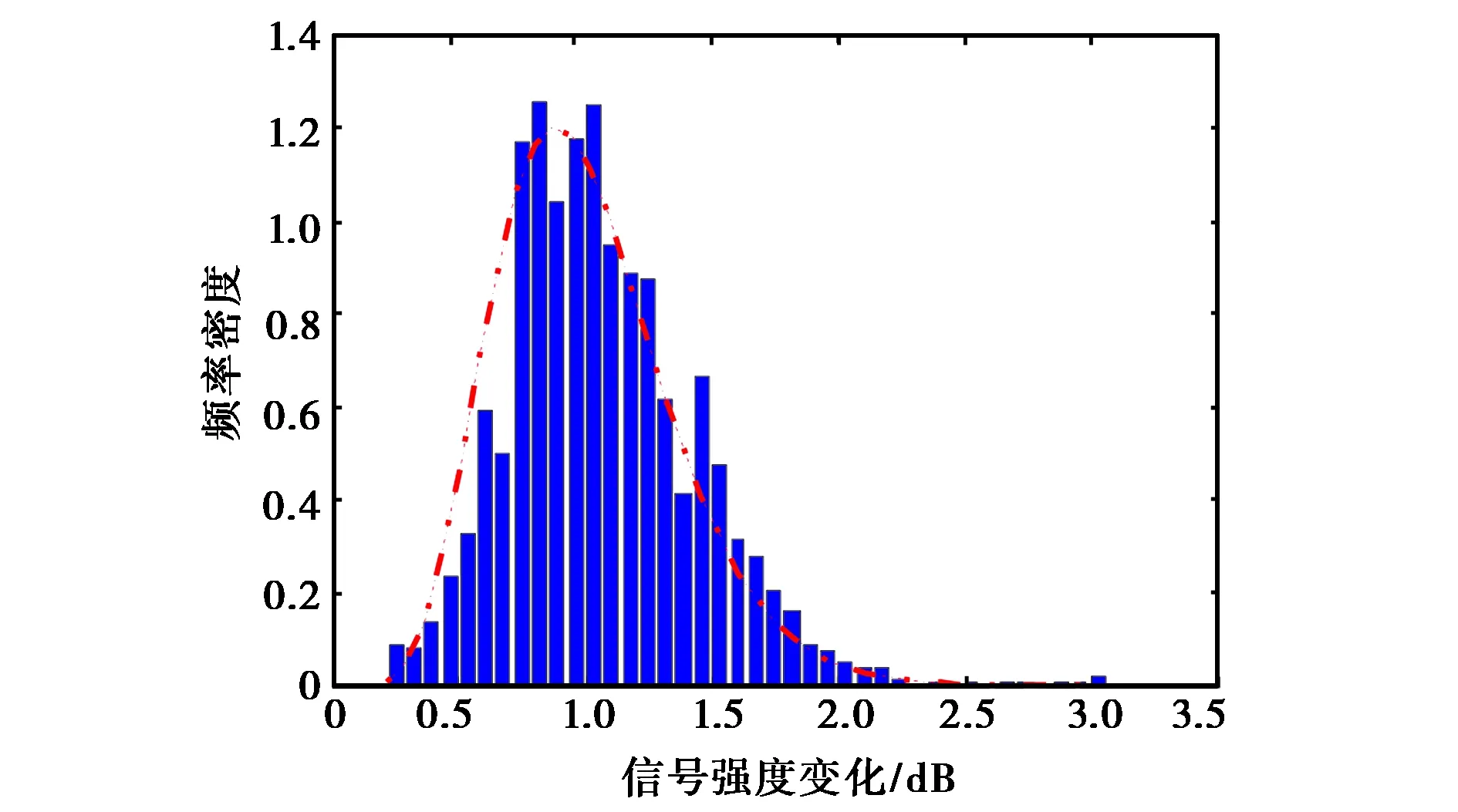
(a) 实测值
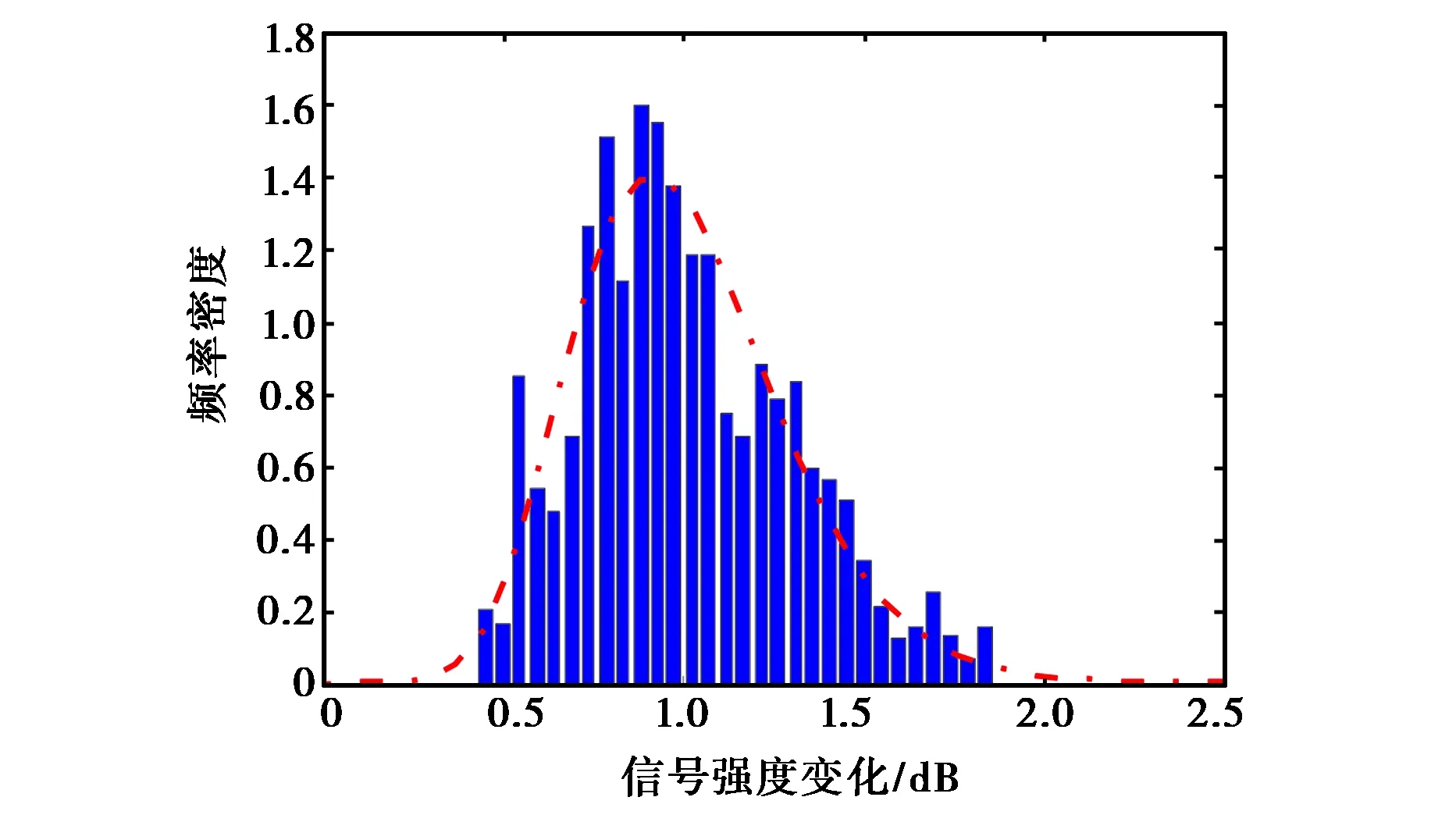
(b) 仿真值图5 电离层闪烁影响下的GNSS信号强度统计分布(柱状图)及理论分布变化曲线(红色曲线)
4.3 信号相位变化的统计特性
由电离层闪烁理论可知,电离层闪烁引起的卫星信号相位变化符合高斯(Gauss)分布[10,12]:
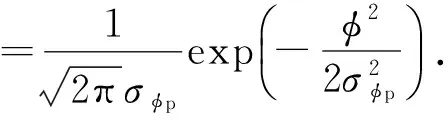
(13)
式中: φ为闪烁引起的信号相位变化; σφp为相位变化方差,该参数也被定义为信号相位闪烁指数,
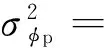
(14)
对实测的闪烁信号相位变化数据进行统计分析,并与理论上的统计模型(Gauss分布)进行比较,Gauss分布中所需参数由实测数据计算相位闪烁指数σφp获得,实测数据计算的σφp为0.13.对相位屏仿真的信号相位变化数据进行同样的分析,利用仿真数据计算的σφp为0.13.图6分别给出了实测数据与仿真数据的比较结果.可以看出:
1) 无论是实测数据还是仿真数据,其相位变化分布均符合相应的Gauss分布.
2) 仿真数据计算的相位闪烁指数σφp(0.13)与实测数据的计算结果(0.13)相等.
由此表明,仿真的闪烁影响下的卫星信号相位变化特性与实际信号相位变化具有一致性.
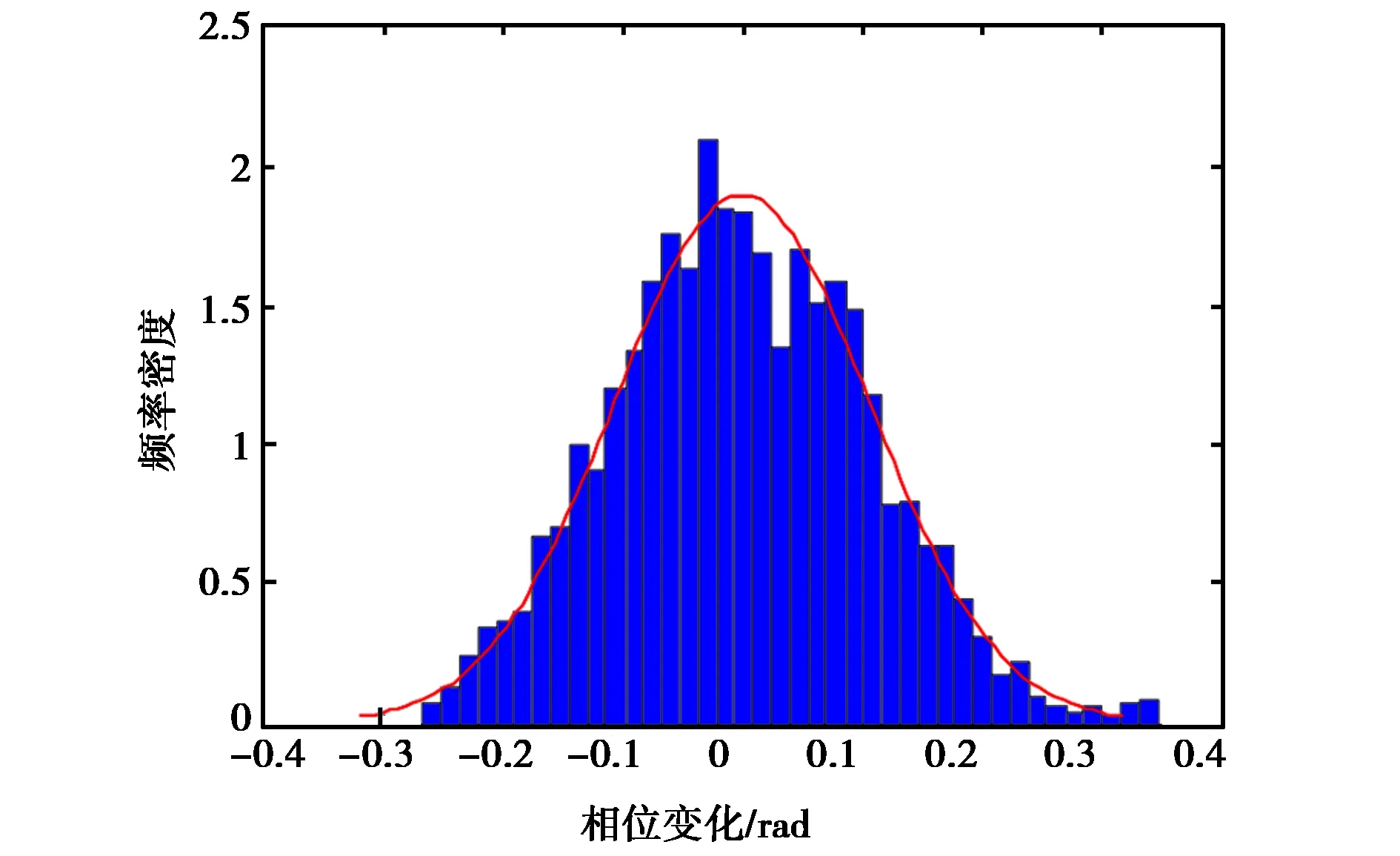
(a) 实测值
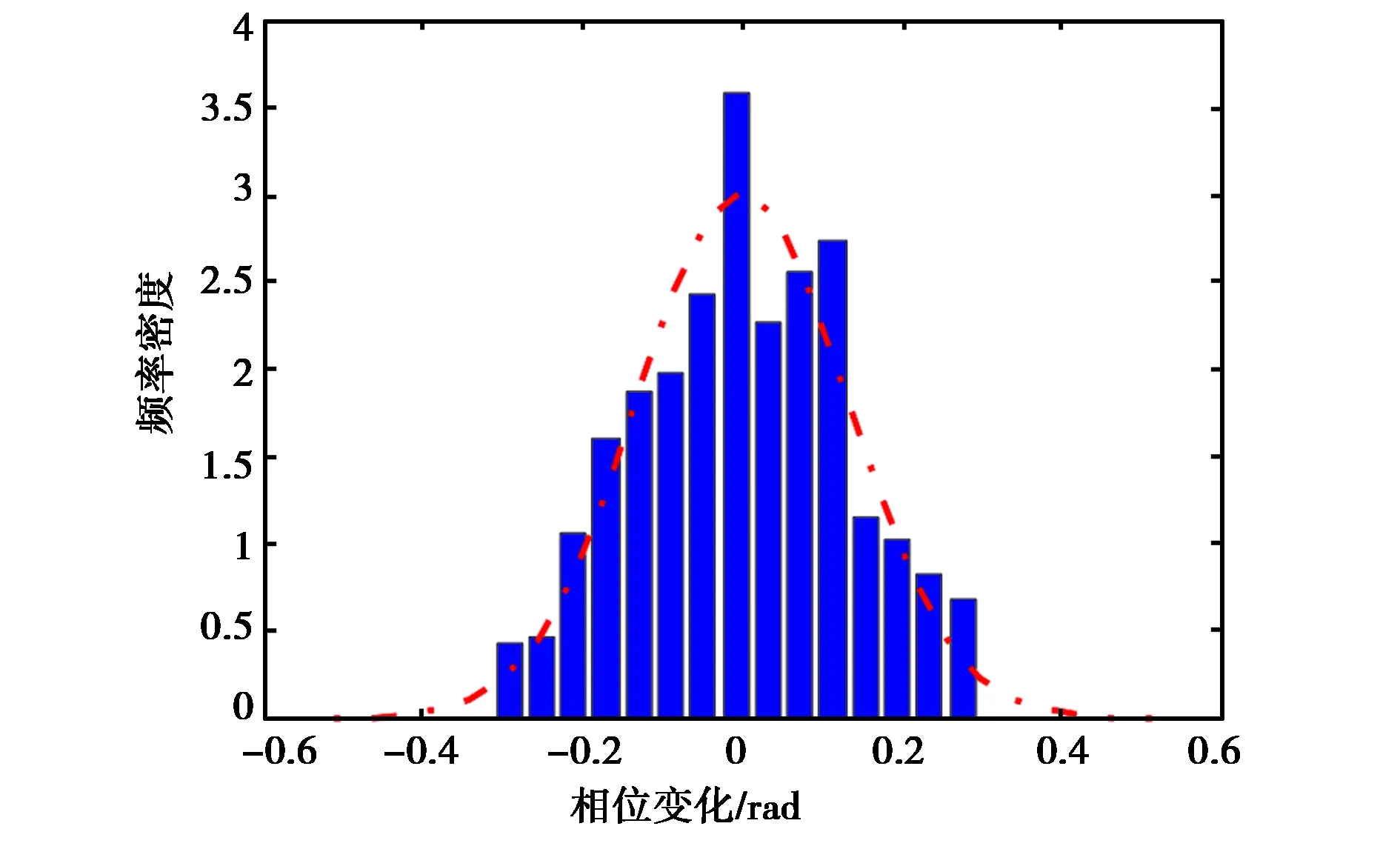
(b) 仿真值图6 电离层闪烁影响下的GNSS信号相位统计分布(柱状图)及理论分布变化曲线(红色曲线)
4.4 信号变化的谱特征
电离层闪烁理论分析表明,在频率大于菲涅尔频率时,幅度谱和相位谱均呈现幂率谱下降趋势,且具有相同变化规律;当频率小于菲涅尔频率时,幅度谱由于菲涅尔滤波效应保持不变或下降,而相位谱保持随频率降低而增大的趋势[12].
菲涅尔频率公式为
(15)
式中:v为不均匀体漂移速度,仿真中取为80 m/s;λ为信号波长,对于北斗B1信号而言约为0.192 m;Z为接收机至相位屏的距离,根据卫星星历和接收机位置计算结果为500 km.因此,菲涅尔频率fF约为0.2 Hz.
对仿真的信号数据进行谱分析,从图7可以看出(为显示谱变化规律的一致性,将幅度谱进行了下移):当频率大于菲涅尔频率时,幅度谱和相位谱具有相同的幂率下降趋势,且与理论曲线吻合;当频率小于菲涅尔频率时,相位谱随频率降低继续增强,而幅度谱出现水平变化.这与理论分析一致[10,12].同时,仿真信号的谱分析结果中,谱强度T(1 Hz处的谱密度)约为-30 dB,与实测数据拟合估计的结果基本相同(见表1).
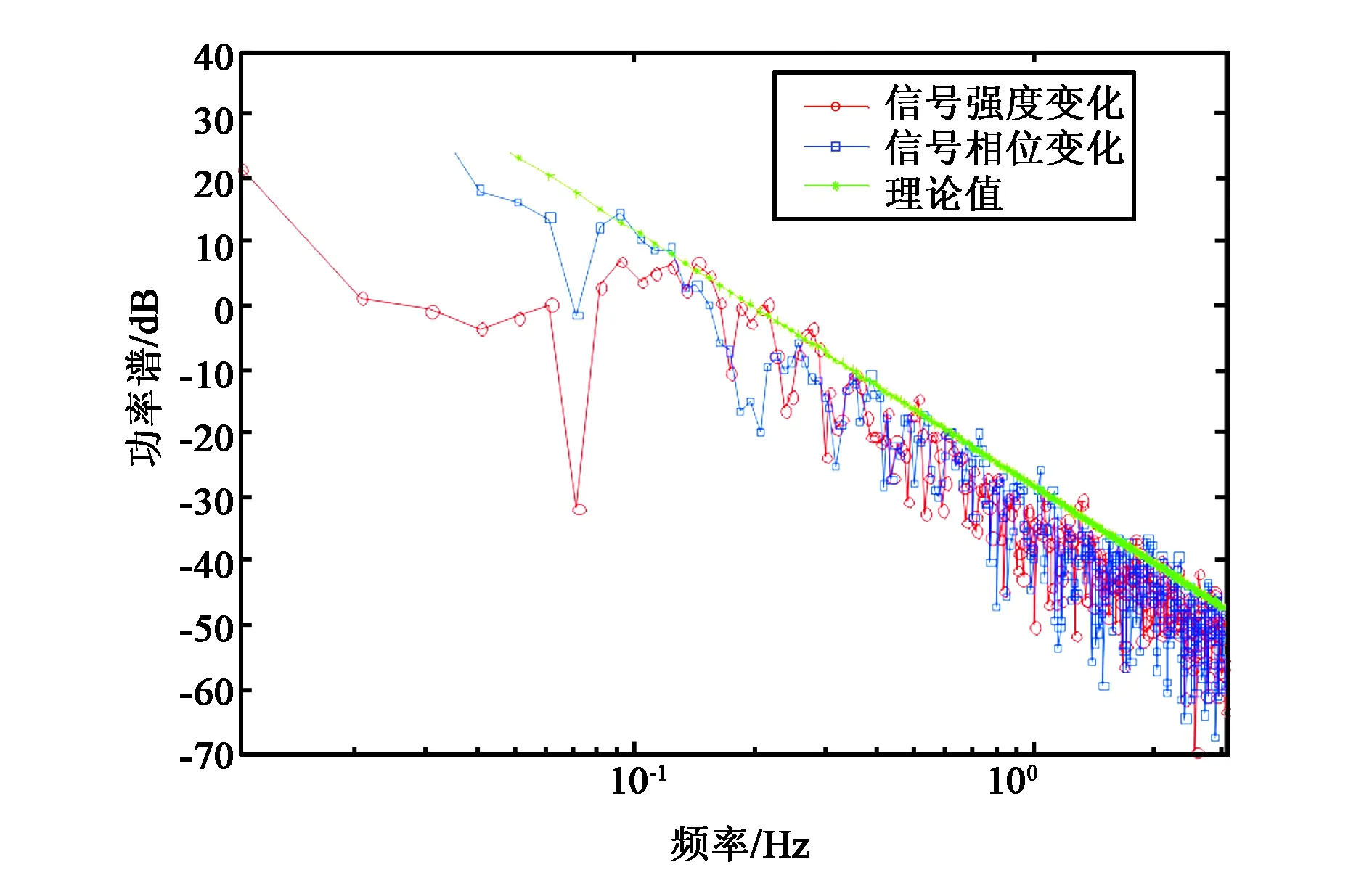
图7 仿真信号的谱分析结果
4.5 关于闪烁强度与电子密度扰动的进一步讨论
由文献[15]可知,电子密度起伏变化均值ΔNe、不均匀体扰动强度Cs,以及不均匀体强度等效参数CkL之间存在下述联系:
(16)
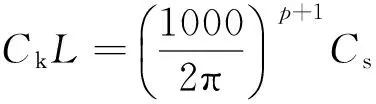
(17)
式中: k0为不均匀体外尺度对应的波数,k0=2π/L0,L0为不均匀体外尺度,仿真中取为10 km; υ=p/2,p为相位谱指数,由实测数据进行谱分析获得,一般取为2.5; L为不均匀体层厚度,一般取为百千米量级,仿真中取为200 km[6].由表1可以看出,利用实测数据估计的CkL约为34,将上述仿真中采用的参数带入式(16)和式(17),可以估计ΔNe的值约为1.6×1011个/m3量级.利用IRI模型计算北斗PRN 1号卫星信号穿刺点位置处(19°N,112°E)在2014年9月13日20:45时的电子密度剖面分布,可知电子密度最大峰值Ne约为1.6×1012个/m3.因此,造成电离层闪烁的电子密度起伏相对于背景电离层电子密度的比值ΔNe/Ne约为10%.该值位于形成闪烁的电离层电子密度起伏范围内(ΔNe/Ne一般不超过20%)[6].
通过上述分析表明,采用相位屏方法可以实现对闪烁影响下的GNSS卫星信号仿真.对仿真信号的时间序列变化,仿真信号的强度、相位统计特征,谱特征以及电子密度起伏的进一步分析比较表明,仿真的结果具有闪烁影响下GNSS信号应有的变化规律,且与实际计算结果具有一致性.
5 结 论
相位屏理论是研究电离层闪烁的一种有效方法,在弱闪烁和中等强度闪烁情况下,相位屏的理论分析结果与实测数据分析结果相符.
利用数字信号处理方法模拟生成相位屏相位扰动,并结合抛物波方程的数值求解,可以建立电离层闪烁影响下的GNSS信号仿真实现方法.
对仿真信号的时间序列变化,仿真信号的强度、相位统计,相位谱特征以及电子密度起伏变化等参量分析表明,仿真结果具有闪烁影响下GNSS信号应有的变化规律,表明基于相位屏理论实现的仿真方法的有效性.
基于相位屏方法建立的GNSS信号电离层闪烁影响仿真方法,可接收实测数据提取的闪烁参数(谱指数、谱强度等),产生与实测数据具有相同变化规律的仿真数据(闪烁影响下的GNSS信号).这对于进一步开展电离层闪烁对GNSS接收机影响分析,电离层闪烁对GNSS系统性能影响分析评估等研究具有重要意义.
致谢:作者在本文工作期间与C.R.Rino先生进行交流,获得Rino先生的宝贵建议,在此表示感谢.
[1] 刘思慧, 刘钝. 电离层闪烁对北斗增强系统影响的建模研究[J]. 电波科学学报, 2015, 30(1): 135-140.
LIU S H, LIU D. Modeling the effects of ionospheric scintillation on BD augmentation system[J]. Chinese journal of radio science, 2015, 30(1): 135-140. (in Chinese)
[2] HEGARTY C, EL-ARINI M B, KIM T, et al. Scintillation modeling for GPS/WAAS receivers[C]//Proceedings of the Institute of Navigation GPS (ION GPS). Salt Lake City, UT, September 19-22, 2000.
[3] CARRANO C S, GROVES K M, CATON R G. A phase screen simulator for predicting the impact of small-scale ionospheric structure on sar image formation and interferometry[C]//Geoscience and Remote Sensing Symposium (IGARSS). Honolulu, HI, July 25-30, 2010.
[4] CARRANO C S, GROVES K M, CATON R G. Simulating the impacts of ionospheric scintillation on L band SAR image formation[J]. Radio science, 2012, 47(4):723-736.
[5] COSTA E, BASU S. A radio wave scattering algorithm and irregularity model for scintillation predictions[J]. Radio science, 2002, 37(3): 1046-1059.
[6] BENIGUEL Y. GIM: a global ionospheric propagation model for scintillation of transmitted signals[J]. Radio science, 2002, 37(3):1032-1044.
[7] FREMOUW E J, LEADABRAND R L, LIVINGSTON R C, et al. Early results from the DNA Wideband satellite experiment—complex signal scintillation[J].Radio science, 1978, 13(1): 167-187.
[8] RINO C L, FREMOUW E. The angle dependence of singly scattered wavefields[J]. Journal of atmosphere and solar-terrestrial physics, 1977, 39(8): 859-868.
[9] RINO C L. A power law phase screen model for ionospheric scintillation, I. weak scatter[J]. Radio science, 1979, 14(6): 1135-1145.
[10]RINO C L. The theory of scintillation with applications in remote sensing[M]. New York: John Wiley, 2011.
[11]RINO C L, Owen J. Numerical simulations of intensity scintillation using the power phase screen model[J]. Radio science, 1984, 19(3): 891-908.
[12]YEH K C, LIU C H. Radio wave scintillations in the ionosphere[J]. Proceedings of IEEE, 1982, 70(4): 324-360.
[13]许正文. 电离层对卫星信号传播及其性能影响的研究[D].西安: 西安电子科技大学, 2005.
XU Z W. Ionospheric effects on satellite radio signal propagation and its performance[D]. Xi’an: Xidian University, 2005.(in Chinese)
[14]KNEPP D L. Multiple phase-screen calculation of the temporal behavior of stochastics waves[J]. Proceedings of IEEE, 1983, 71(6): 722-737.
[15]ROBINS R E, SECAN J A, FREMOUW E J. A mid-latitude scintillation model[R]. Bellevue WA: Northwest Research Associates Inc, 1986.
[16]SECAN J A, BUSSEY R M, FREMOUW E J, et al. An improved model of equatorial scintillation[J]. Radio science, 1995, 30(3): 607-617.
刘钝 (1973-),男,河北人,中国电波传播研究所高级工程师,主要研究方向为电波传播应用技术、GNSS应用技术研究.

於晓 (1982-),女,湖北人,中国电波传播研究所工程师,主要研究方向为电离层闪烁建模技术研究.

冯健 (1981-),男,山东人,中国电波传播研究所高级工程师,主要研究方向为电离层闪烁建模技术研究.
Simulating the impacts of ionospheric scintillation on GNSS signals with phase screen method
LIU Dun YU Xiao FENG Jian ZHEN Weimin
(ChinaResearchInstituteofRadiowavePropagation,Qingdao266107,China)
A phase screen model based Global Navigation Satellite System (GNSS) scintillation simulation is developed for predicting the impacts of ionospheric scintillation on GNSS signals. The method consists of the phase screen generation and solution of parabolic wave equation (PWE). The 2-D realization of spatial phase fluctuation is realized by passing a normally distributed, zero-mean random sequence through a special designed filter based on the power spectral density (PSD) function. The parabolic wave equation is solved using the split step technique to compute the complex amplitude reaching the receiver antenna. It accounts for the oblique propagation of the GNSS signals and the characteristic parameters of scintillation-producing irregularities, all of which determine the strength of scintillation and could be retrieved from measurements. Ionospheric scintillation impacts on GNSS signals is simulated with the parameters for observation from low-latitude areas in China. Comparison is also conducted from various aspects with the simulated signal and that of field observation, including the amplitude variation, statistics characteristics of intensity and phase, spectral analysis of signal time sequence. It demonstrates that GNSS scintillation simulation can reproduce the scintillation impacted GNSS signals, and the outputs are consistent with the theory analysis and the field data analysis, which show the validity of the GNSS scintillation sinmulation.
ionospheric scintillation; irregularity; phase screen; parabolic wave equation (PWE); Global Navigation Satellite System (GNSS); simulation
10.13443/j.cjors.2015083102
2015-08-31
P228.4;P352
A
1005-0388(2016)04-0632-07
付海洋 (1983-),女,黑龙江人,博士,复旦大学信息科学与工程学院讲师, 主要研究方向为空间等离子体物理、高功率电磁波和等离子体的相互作用、空间电离层主动改性实验等.
刘钝, 於晓, 冯健, 等. 电离层闪烁对GNSS信号影响的相位屏仿真方法[J]. 电波科学学报,2016,31(4):632-638.
LIU D, YU X, FENG J, et al. Simulating the impacts of ionospheric scintillation on GNSS signals with phase screen method [J]. Chinese journal of radio science,2016,31(4):632-638. (in Chinese). DOI: 10.13443/j.cjors.2015083102
联系人: 刘钝 E-mail: DUN.L@163.com

