关于“近世代数”教改的探讨

赵志兵

(安徽大学 数学科学学院，合肥 230601)



关于“近世代数”教改的探讨

赵志兵

(安徽大学 数学科学学院，合肥 230601)

“近世代数”是高等学校数学专业的重要基础课程之一，主要讲授的是群、环、域等代数系统的基本性质和相关的应用。通过简单分析这门学科的特点和当前教学的现状，结合自身的教学实践，在教学内容和教学方法上给出了关于“近世代数”课程教学的几点建议。

“近世代数”；课程教学；教学改革

“近世代数”又称抽象代数，产生于19世纪上半叶，区别于以往的初等代数以解方程为主，“近世代数”主要是研究各种抽象的公理化代数系统。大学阶段的“近世代数”课程是高等学校数学专业的重要基础课程之一，主要讲授的是群、环、域等代数系统的基本性质和相关的应用，它以高等代数(或线性代数)为其先修课程，又是代数数论、代数几何、代数拓扑以及同调代数等课程学习的基础课程。

现行的“近世代数”课程的教学主要以传统的教学方式为主，多是抽象的概念加抽象的定理，再加上抽象的证明题作为作业；教学内容一般都是从预备知识出发，然后到群，再到环，最后是域，往往忽略了“从哪里来，到哪里去”的基本问题。 本文首先简单的分析了“近世代数”的学科特点和当前的教学现状，后结合笔者在本学科教学过程中的实践，从教学内容和教学方法上给出本课程教学的几点建议。

1 学科特点和当前教学现状

1.1 学科特点

一方面，代数学科的主要特点就是其概念、定理众多，其习题以证明题为主，抽象程度高、逻辑性强，使得初学者难以很好的把握。其思想和研究方法，对其他学科产生了越来越大的影响，如“近世代数”中的等价、划分、同构等思想方法不仅是重要的数学方法之一，同时也是观察和研究自然和社会的普遍采用的方法。[1]

另一方面，“近世代数”在其他的数学领域有着广泛的应用，特别是对数学发展中很多有重要历史意义问题的解决起了关键性作用，如高斯二平方和的问题、代数基本定理的证明、尺规作图、三等分角等问题的解决。此外，“近世代数”在其他的学科中又有非常广泛的应用，例如20世纪初，群论应用于理论物理与分子化学中，而理想理论与(有限)域理论在计算机理论、编码与信息安全等领域的应用更被认为是近代纯粹数学应用的一个成功范例。[2]

1.2 当前教学的现状

由于“近世代数”作为纯数学学科的的特点，其抽象程度较高，和现实生活联系较少，使其成为一门难学难懂的学科。而在高校毕业生就业压力大，用人单位更强调毕业生的实践创新能力的大环境下，更使得学生对一些纯粹的理论学科的学习积极性受到影响。在传统的“近世代数”课程教学中，很多是单纯地追求概念的抽象性、逻辑的严密性、结论的明确性和体系的完整性，这样更会容易使得“近世代数”课程的知识与现实脱节，导致一些学生感到“近世代数”枯燥乏味、无用，从而直接影响了学生对“近世代数”课程和后继相关课程的学习热情。所以，有必要对“近世代数”课程的教学进行必要的改革，包括教学内容、教学方法和一些教学手段。

2 教学改革的几点建议

2.1 教学内容

现行“近世代数”教学的内容主要包括群论、环论和域扩张理论，而群论的内容通常会占到整个教材篇幅的一半左右。大学的“近世代数”课程的课时数一般在70课时，有教学经验的教师都知道，利用70个左右的课时将“近世代数”中3方面的内容都透彻讲完整是很困难的，虽然一般的“近世代数”的教材篇幅不是很长，但包含的信息量是很大的。所以在实际的教学过程中，大部分的老师都会面临“上不完”的问题，即使能上完，部分内容也讲不完整。因而，很多教师就对教材的内容进行删减，比如群论的sylow定理、群作用以及有限Abel群的结构通常都在被删减的内容之列，笔者认为这些内容恰是群论中最精彩和重要的内容之一，当然也是最难的部分，而“难”可能是其通常被删减的重要原因。

我们以为，教学的内容要回归课程的本原。大家都知道，“近世代数”起源于Abel，Galois等人解决5次及其5次以上的方程的求根公式的存在性问题，但随着学科的发展，现在的教材很大程度上偏离了这个本原，甚而我们难以回答学生诸如“为什么要学‘近世代数’”“学“近世代数”有什么用”的问题。在实践教学的过程中，大部分教师通常是按照从群到环再到域的思路走，这样做从逻辑上是无可厚非的，因为群是比环来得“容易”的代数系统，它只带有一个运算，而域是一种特殊的环。事实上，学生首先接触的是环和域，大家最熟悉的整数集就是带有“加法”和“乘法”两个运算的一个典型的环，而高等代数中学生也接触到了数域和一元多项式环。

因而建议可以先讲环论的基本知识，后转入群论的基本知识，再转入域论，最后再来讲群论中难点问题，如Sylow定理、群作用等。这样处理的一个好处是，在课程开始的阶段我们就可以引入问题：如何证明代数基本定理的证明？如何解决高次方程求根公式的问题？在完成域论的课程后，我们就可以给出上述问题的一个解答，而不至于学生在学完Sylow定理和群作用后已经“筋疲力尽”了，到最后还是没有弄清楚“近世代数”是从哪里发展起来的，“近世代数”有什么用。通常情况下，没有足够的课时去讲Galois理论，因而尺规作图问题、数的超越性问题可以留给有兴趣的学生自己去解决。[3]群论中的精彩部分，如Sylow定理、群作用等内容可以作为“近世代数”的研究和发展所得到的成果介绍给学生。

2.2 教学方法

(1) 注重课程之间的衔接。这里的衔接指的是和前修课程的衔接以及和后续课程的联系。

大学阶段的“近世代数”课程的前修课程主要指高等代数，当然“近世代数”中的某些例子也会涉及到数学分析和解析几何的相关知识。教师在讲授“近世代数”课程的过程中要尽可能多的利用高等代数中已有的知识给出所需要的例子；例如，在讲授等价关系时，矩阵间的等价、相似、合同就是非常好的例子。在讲授环论的时候，数域上的一元多项式环就是一个大家熟悉和已知的例子，也可以用矩阵作成的环(数域上阶全阵环)为例来引入和说明环的一些基本性质，特别是关于其元素的一些性质(单位元、交换性、零因子、可逆性等)。这样处理既可以起到一定的“复习”效果，又可以让学生在接受新知识时不至于感到太陌生和太抽象。

有些学校在“近世代数”后面会开设一些代数方向较专业的课程作为选修课，如Galois理论、同调代数、群表示论等，以满足一些学有余力和对代数方向感兴趣的同学的学习要求。这就要求教师在讲授“近世代数”的过程中注重其与这些课程之间的衔接，以激发学生继续学习的积极性。如在讲授域扩张时，就可以把更多的可以利用Galois理论解决的问题抛出来，如尺规作图问题、π的超越性等。又如在讲群作用的时，可以引入群表示的概念，并简单的说明下群作用和群表示之间的一一对应关系，从而可以引出群表示论。

(2) 研究性教学法。研究性教学法，就是在实际的教学过程中，教师不断的提出与教学内容相关的问题，并指导学生理解和解决这些问题。基于“近世代数”学科的特点，此课程非常适合研究性教学法。下面来看几个简单的例子。

例1 对于群的定义，文献[4]中是这样定义的：一个非空的带有一个代数运算的集合称为群，指的是其满足3条：1)结合律成立；2)存在“左”单位元；3)每个元素存在“左”逆元(通常称之为“左左”定义)。

问题1：其中的2)，3)条是否可以换成2)′存在“右”单位元和3)′每个元素存在“右”逆元？(通常称之为“右右”定义)

问题2：其中的2)，3)条是否可以换成2)和3)′，或者类似的换成2)′和3)？

分析 问题1的答案是肯定的，即群定义中的“左左”和“右右”是等价的。问题2的答案是否定的，具体可参见文献[2]中的例4。问题的提出是自然的，学生在寻求答案的过程中会更加深刻的理解群的概念，这对初学者是非常重要的。另外，也使得学生对“左”单位元(逆元)与“右”单位元(逆元)以及单位元(逆元)理解更透彻，从而使学生清楚不同教材中对于某些概念的定义可能形式上不同，本质上却是等价的，如在文献[5]中，对群的定义就直接要求单位元和每个元素的逆元存在。

例2 设H和K分别为群G的两个非空子集，定义它们之间的乘积为

问题：HK=KH(即集合乘积可交换)是否等同于两个集合中的元素乘积可交换，即对

h∈H,k∈K，有hk=kh？

分析 HK=KH不能推出两个集合中的元素乘积可交换，具体可参见文献[6]中的例1；反过来，若H和K中的元素乘积均可交换，自然有HK=KH。

学生通过对上述问题的分析，能更清楚的把握“整体”运算和“个体”运算之间的联系，整体运算本质上是转化为一个个“个体”之间的运算，从而“个体”可以决定“整体”的性质，反过来“整体”却不够精细。

在“近世代数”教学中，应该始终带着问题教，这样可以让学生带着问题学。时间长了，学生会由被动问问题转为主动问问题，学生的学习积极性提高了，教师的上课热情也增长了，从而达到教学相长，互相提高。又如在讲授Langrange定理的时候，自然的问题是它的逆命题是否成立，这样引入Sylow定理就比较自然。学习过程中多提这样的问题会使得学生在学习过程中逻辑上更清晰，目标也更明确。

(3)注重具体例子的作用。代数中的例子有说明概念或命题的正例也有说明命题否定的反例，值得一提的是，利用反例说明一个命题的否定性是“近世代数”一个常用的技巧和手段。

A．抽象的概念和命题与例子相结合。“近世代数”学科的一个重要特点就是抽象，概念多，因而学好“近世代数”应该从掌握和理解其基本的数学概念入手。数学概念是现实世界中空间形式和数量关系及其特有属性在人的思维中的反映[2]，在教学过程中，当讲解一个新的概念或知识点时，教师应有意识地剖析几个比较典型的具体例子，让它们起到一个模型和示例的作用，这有助于学生对抽象的概念的理解和把握。

比如，在学习群的过程中，首先以学生熟悉的整数加群和非零有理数乘群为例简单的按群的定义验证下，后再结合高等代数的知识给出数域F上的一般线性群GLn(F)，在此基础上，再介绍相对比较抽象的n次单位根群和四元数群。这样，由熟悉到相对不熟悉，有较具体到抽象的给出说明“群”这个概念的一些例子，容易让学生接受也符合学生学习、认识事物的一般规律。

例如在学习环的同态基本定理后，可以给出下面一个自然的例子。

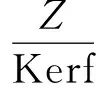
总之，在介绍抽象的概念和命题的时候，通过剖析一些具体的例子，由浅入深的对概念和命题给出解释，将抽象的概念和命题具体化，有助于学生更好地理解和掌握抽象的概念和命题。

B．强调反例。“近世代数”学习过程中，众多的概念和命题的理解需要层层剖析才能把握其本质。对概念，不仅要理解概念本身，还要把握它的对立概念；而对于一些命题的条件和结论的把握更需要给出有力的反例来说明，从而使学生更加深刻的理解概念和命题的本质。

例4 一个群G的子群N称为其正规子群指的是对于∀g∈G，均有gN=Ng。

反例 3次对称群S3的子群H={(1),(12)}就不是其的正规子群，原因是

H(23)={(23),(123)}≠{(12),(132)}=(23)H。

例5 一个整环称之主理想整环，指的是其每个理想均是由一个元素所生成的主理想。

反例 考虑整数环上的一元多项式环Z[x]，其理想<2,x>指的是Z[x]中所有常数项为偶数的多项式构成的Z[x]的理想，它不是一个主理想，事实上，若设=<2,x>，则有2∈,x∈，从而f(x)=1，这与<2,x>指的是Z[x]中所有常数项为偶数的多项式构成的Z[x]的理想矛盾！

例6 对于群中元素的阶，有结论：若群中元素a的阶为m，元素b的阶为n，则当ab=ba且(m,n)=1时，ab的阶为mn。

另一方面，容易得到群中元素a与其逆元a-1具有相同的阶，且自然有aa-1=a-1a=e。若a的阶为m(>1)，则显然有e的阶为1，不等于m2，因而条件(2)不可少。

3 结束语

“近世代数”教学内容顺序上的调整是为了更好的使其跟前学课程衔接和体现本课程本原的想法。“近世代数”教学方法更是多种多样，除了我们重点阐述需要加强的几个方面，还有类比法、对比法以及一些其他传统的教学方法的运用等。总体而言，学生是学习的主体，“近世代数”的教学内容和教学方法上的改革必须贯彻以学生为主, 通过各种教学手段和教学方法的改进来提高学生对该课程的学习兴趣, 激发学生对本学科的学习热情，锻炼学生的逻辑思维、抽象思维能力，培养学生自主学习的能力以及发现问题的能力。“近世代数”课程的目标是使学生通过本学科的学习了解代数学的基本思想，掌握代数学研究的基本方法, 把握具体与抽象、一般与特殊的辩证关系, 为后续的学习和工作打好良好的代数学基础。

[1] 郭华光, 徐祥, 裴定一．近世代数课程教学内容的改革与实践[J].广州大学学报(自然科学版)，2003, 2(6)：587-590．[2] 袁玉卓，王骁力．关于近世代数课程教学的一些建议[J].南阳师范学院学报，2012,11(9)：90-92.

[3] 章璞．伽罗瓦理论：天才的激情[M].北京：高等教育出版社，2013 .

[4] 杨子胥．近世代数[M]．2 版．北京：高等教育出版社，2003:31.

[5] 刘绍学．近世代数基础[M]．北京：高等教育出版社，1999:13.

[6] 何立官，陈贵云，罗萍．近世代数中关于商群、商环乘法的理解[J].西南师范大学学报(自然科学版)，2012, 37(10)：31-34．

[责任编辑：张永军]

Discussions on Education Reform ofModernAlgebras

ZHAO Zhi-bing

( School of Mathematical Sciences，Anhui University，Hefei 230601，China)

ModernAlgebrais one of the important basic courses for mathematical majors in high school．It’s contents included mainly basic properties and some related applications of some algebraic systems, such as groups ,rings and fields. In this paper, the characteristics ofModernAlgebraand the current course teaching situations are discussed．And we give some suggestions on how to improve the teaching quality inModernAlgebrateaching on teaching content and teaching methods by the author’s own teaching practice and experience in it．

ModernAlgebra; course teaching; education reform

2016-08-01

安徽省教育厅自然科学重点项目(KJ2015A101)、安徽大学研究性示范课程项目(J10118443005 )资助。

赵志兵(1979—),男，安徽桐城人，安徽大学数学科学学院讲师、博士。

O153

A

2096-2371(2016)04-0123-04