基于多支持向量机和粒子群算法的永磁同步直线电机优化设计

徐道际

(安徽宏实光机电高科有限公司，合肥 230601)



基于多支持向量机和粒子群算法的永磁同步直线电机优化设计

徐道际

(安徽宏实光机电高科有限公司，合肥 230601)

引入多支持向量机算法(MSVM)，用以解决永磁同步直线电机(PMSLM)优化设计中的快速建模问题。在3D有限元分析的基础上，采用MSVM拟合直线电机结构参数与运行性能参数之间的非线性关系，对电机性能参数(推力、推理波动率、效率和谐波畸变率等)进行回归预测，该方法建立的模型精度可达到93%以上；引入粒子群算法(PSO)对MSVM电机模型进行寻优，得到一组最优的电机结构参数并建立有限元模型。仿真实验结果表明: 采用MVSM建模并优化的电机推力大、推力波动小、峰值电流小、效率高，符合电机的优化设计目标。

直线电机;多支持向量机;推力波动;谐波畸变率;粒子群算法

0 引 言

微秒激光雕刻机的高速非接触式加工，可以最大限度地降低物件的机械形变，提高加工精度，应用于激光雕刻机高速进给系统的永磁同步直线电机(PMSLM)，具有推力密度大、损耗低、响应速度快等优点, 可以实现高速大行程运动和微米级动态精度。[1]推力波动的存在大大降低了电机动子的定位精度，影响机床的性能指标，本文从电机结构出发，建立非参数快速计算模型，进行结构参数优化设计，降低推力波动，改善电机运行性能。

直线电机本体优化设计问题是多目标非线性问题，优化过程需要大量迭代计算，因此需要建立快速计算模型，为优化过程提供实时数据输出。文献[2]采用解析法建立电机模型，这种建立于等效磁化电流的解析模型因为等效假设条件的存在，导致定量计算精度较低；文献[3]采用有限元法建立电机模型，计算精度大大提高，但是计算效率较低，无法满足优化计算过程中实时性要求；MSVM是近期提出的一种基于最小二乘法的回归分类算法，已成功应用于机器学习和高性能回归计算等多个领域，[4]具有多输入多输出性能，可以为永磁同步直线电机优化设计提供较好的模型支持。

以动圈式双次级永磁同步直线电机为研究对象，在3D有限元(3D-FEA)分析的基础上，引入多支持向量机算法(MSVM)，将影响电机性能的结构参数：永磁体高速、气隙、极距、线圈长度等参数作为输入，电机的推力、推力波动率、谐波畸变率作为输出，对电机结构参数与运行性能之间的映射关系进行非线性拟合，将有限元分析的离散数据点进行高精度回归预测，建立高学习能力和泛化能力的快速计算模型，应用粒子群算法对模型进行迭代寻优，得到一组最优的电机结构参数，实现电机谐波畸变率的抑制、推力的增加和推力波动的降低，提高电机的运行性能。

1 多支持向量机算法

支持向量机(SVM)回归问题的实质是寻找一个实值函数f(x)，以求解任一输入x所对应的输出值y，将函数输入向量映射到高维特征空间，在高维特征空间中构造线性回归函数， 使模型的结构风险最小化，[4]将回归问题转化为约束优化问题，对目标函数值进行回归预测。

多支持向量机回归算法(MSVM)[5]是在目标函数为多输入和多输出情况下提出的一种SVR算法，MSVM模型的建立是在单支持向量机的基础上完成， 基本思想是: 首先将一个原始样本数据空间拆分成若干个子空间，然后分别在子样本空间上建立单SVM模型，引入融合算法对多个单支持向量机模型进行数据融合， 建立多输出支持向量回归机。算法如下：对于M维输入，N维输出的函数拟合问题，设训练样本集{(xi,yj)},i=1,2,…,L,j=1,2,…,Lxi∈RM,yj∈RN,构造回归函数如下：

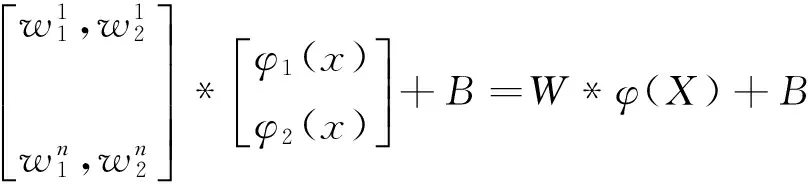
(1)

其中，

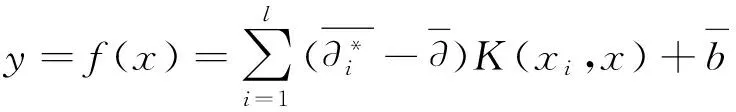
(2)

K(xi,x)=[φ(xi)*φ(x)]，

(3)

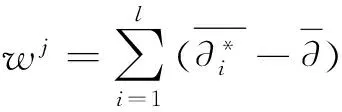
(4)

B=[b1,b2…,bn]。

(5)

将已知样本数据空间拆分成m个子样本数据,每个子样本数据均对应一个输出量,建立各输出量的单支持向量机模型，得到如式(2) 所示的m个函数表达式f(x)。将单SVM函数表达式代入式(1) 中，计算W和B， 得到多支持向量机函数表达式F(x) 根据结构风险最小化原则， 对W和B进行寻优，将回归问题转化为约束优化问题，即：

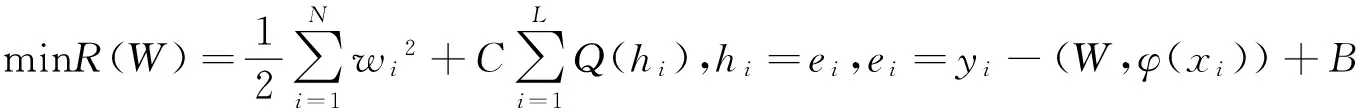
(6)

采用迭代方法求解最小值，并返回到式(1) 中， 得到最优的多输出回归函数。

2 电机非参数模型建立

2.1 建模数据的获取

本文研究的动圈式双次级永磁同步直线电机如图1所示，定子材料为电工纯铁，磁钢材料是汝铁硼N48H，极对数是32，定子槽数为12。

影响电机性能的主要结构参数包括永磁体尺寸、 线圈尺寸和气隙尺寸， 其中， 永磁体尺寸影响电机的转速和功率质量比， 线圈尺寸反映电流承载能力和电机实际体积， 气隙尺寸直接影响电机推力波动。PMSLM的优化设计问题是一个多维非线性问题，需要计算出不同电机结构参数下电机的输出性能参数，如：推力F、电流I、效率e、谐波畸变率η%等。采用有限元方法，根据电机结构参数(表1所示)，建立电机3D有限元(3D-FEA)模型(如图2)。

表1 永磁同步直线电机结构参数 mm

图1 永磁同步直线电机

3D-FEA模型计算效率较低，无法满足优化过程中实时计算的要求，需要建立快速计算模型，采用正交实验设计和随机试验设计相结合的方法[6]，在电机结构参数空间取值范围内，通过有限元仿真得到不同结构参数下的推力F、推力波动率η%、电流I等，作为后续极限学习机非参数建模的数据，200组样本数据如表2。

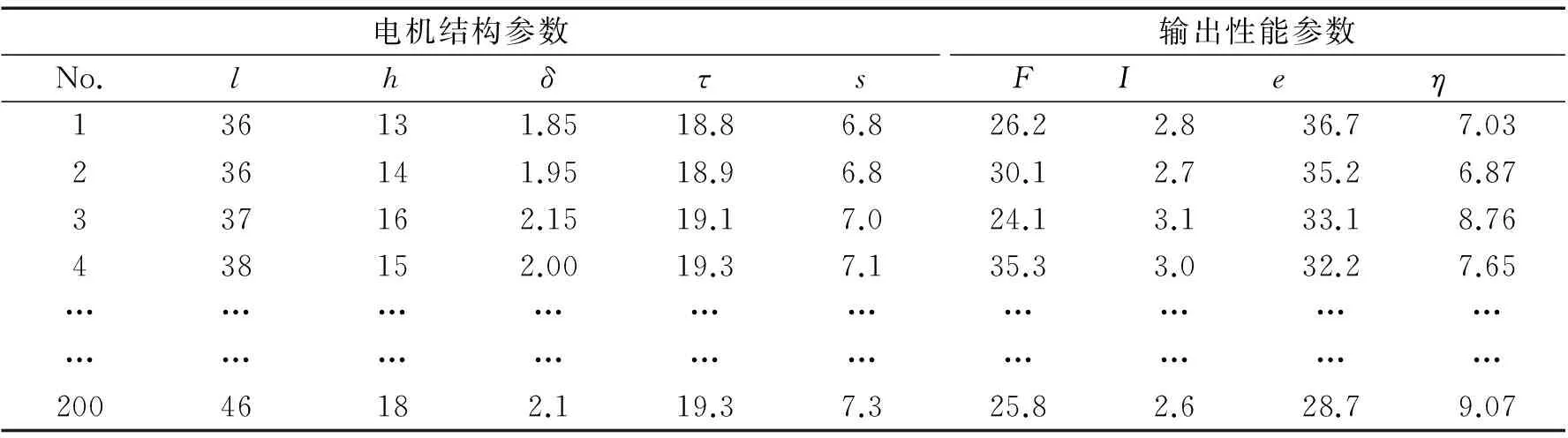
表2 样本数据

2.2 样本数据预处理

由于样本数据中有5个结构参数和3个输出量的数量级有较大差异，为了避免误差，对数据进行归一化处理，将表2中数据归一化到[0,1]区间内，采用映射为：

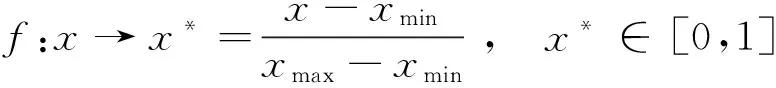
(6)

2.3 模型参数选择

电机多支持向量机模型采用表2样本数据空间中100组数据作为训练集，其余100组数据作为测试集进行回归拟合。首先建立单SVM模型，利用交叉验证法选取惩罚参数C， 并求解各个模型的核函数系数ρ1，ρ2，四个单SVM 模型的相关参数如表 3 所示，MSVM参数W和B如表4所示。

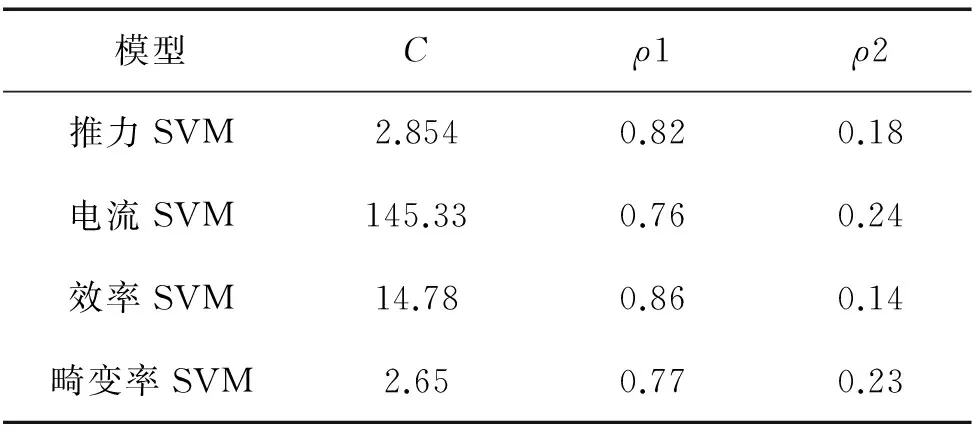
表3 单支持向量机模型参数

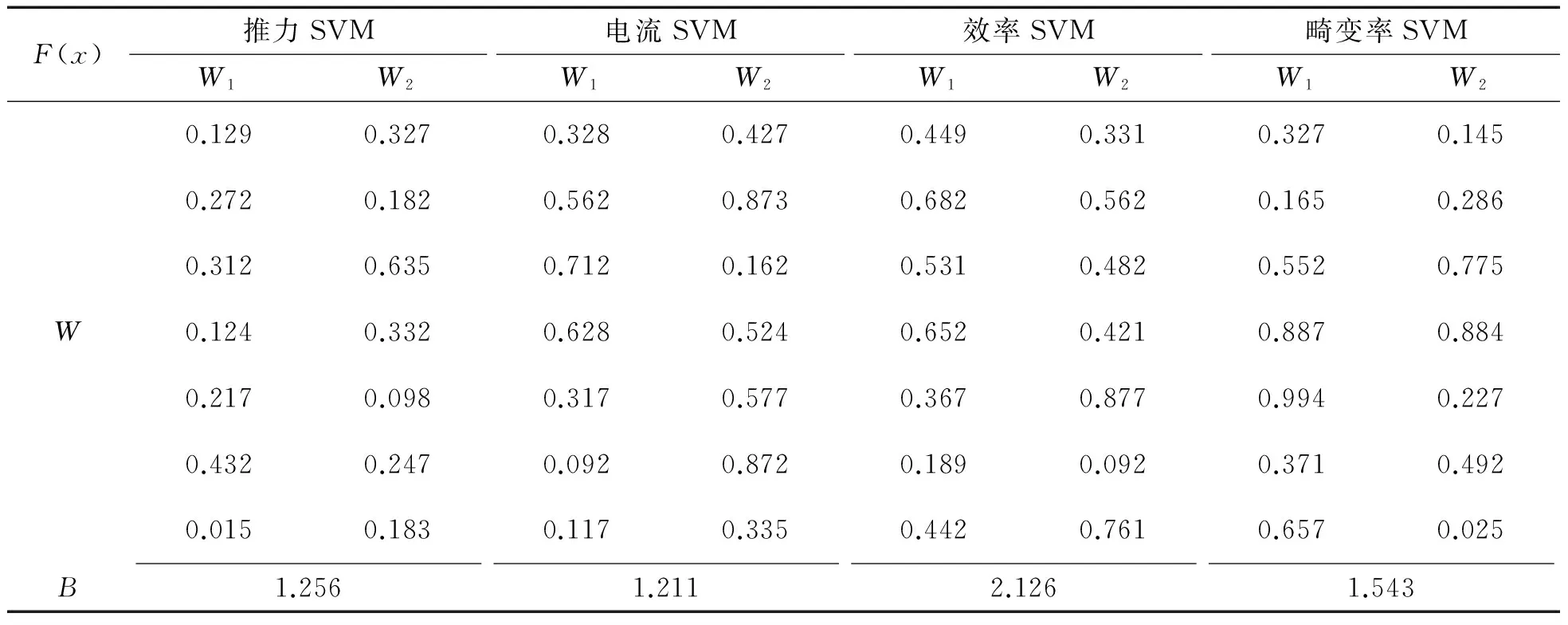
表4 多支持向量机模型参数

2.4 模型性能评价

根据表2样本空间数据和模型参数建立电机MSVM模型，为了检验电机极限学习机模型对电机平均推力值、 电流值、 电机效率和空载反电动势谐波畸变率的预测效果， 对模型的准确性和拟合精度进行评估，结果如表5及图3—6所示。

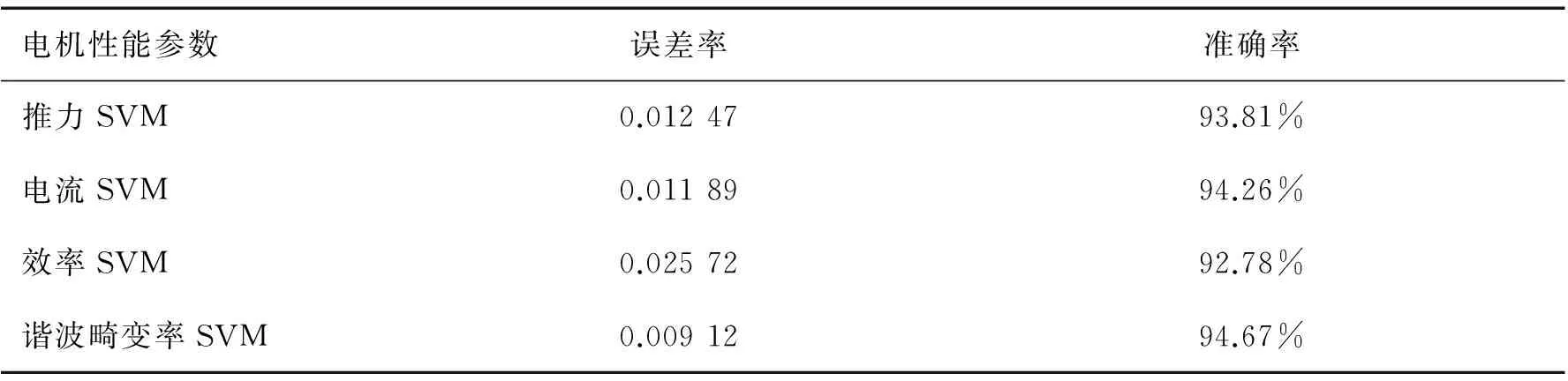
表5 多支持向量机模型精度

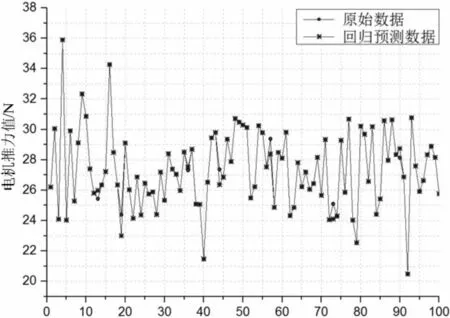
图3 推力值对比图

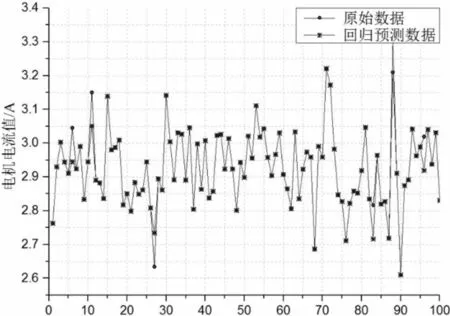
图4 电流值对比图

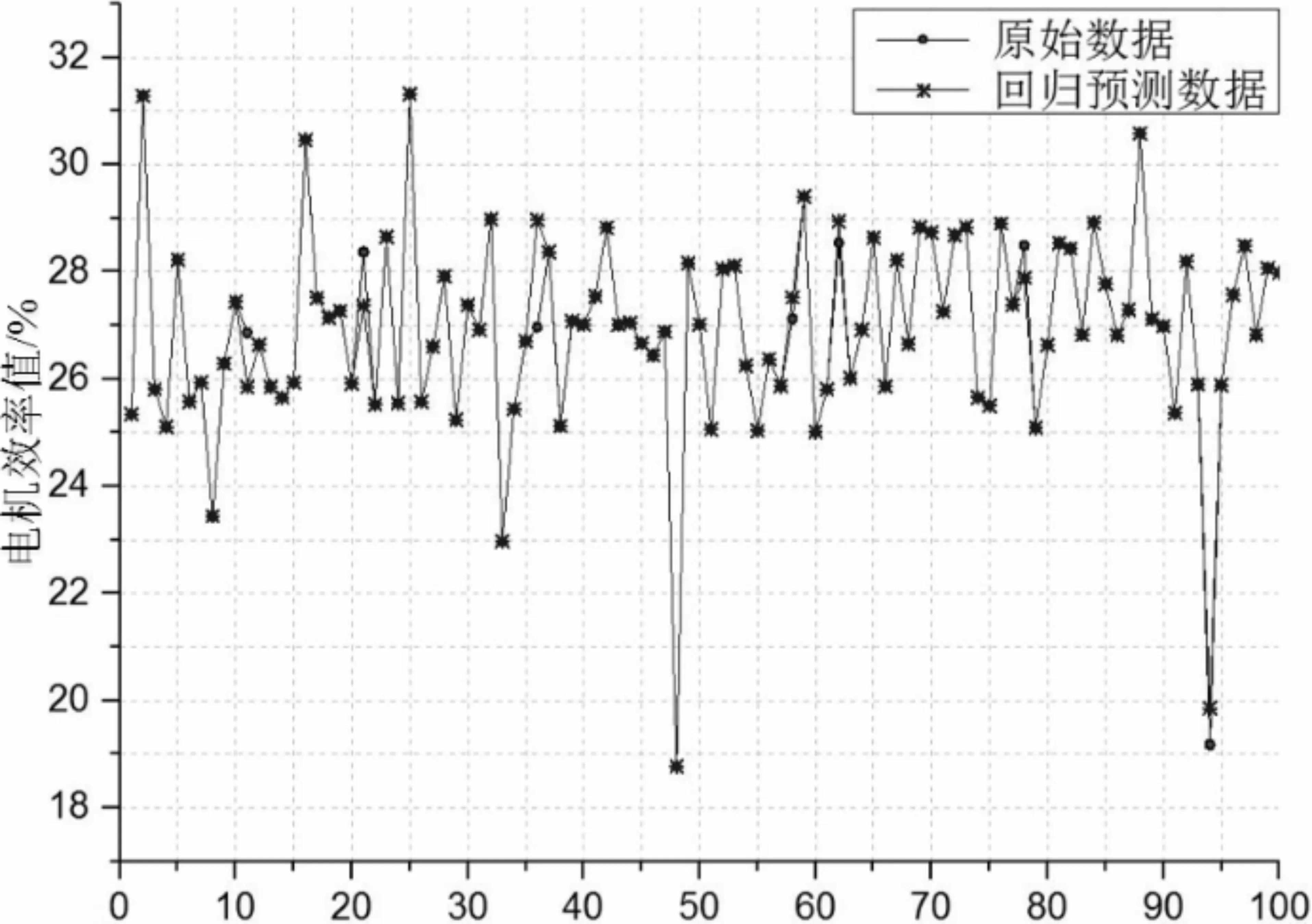
图5 效率值对比图

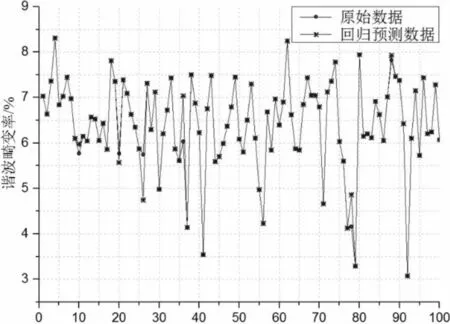
图6 谐波畸变率对比图

分析可知，原始数据与回归数据之间有较好的拟合性，该模型对未知数据的预测准确性高达93%左右，误差率在2%左右，可为后续智能算法对电机结构优化的逆向计算提供较好的数学支持。

3 电机优化

粒子群算法(PSO)[7-9]是一种新型智能算法，是在对动物集群活动行为观察基础上，利用群体中的个体对信息的共享使整个群体的运动在问题求解空间中产生从无序到有序的演化过程，从而获得最优解。相对于一般智能算法，PSO的收敛速度较快，在探索能力和开发能力的平衡上效果更好，具有较高避免陷入局部最优的能力，可以定位目标函数全局最优值，本文采用PSO对电机极限学习机模型进行寻优，经过261次迭代计算后，得到一组最优的电机结构参数，如表6所示。

表6 电机结构参数对比

根据优化后的电机结构参数，建立电机有限元模型，仿真实验结果如图7—9所示。

图7 推力曲线对比

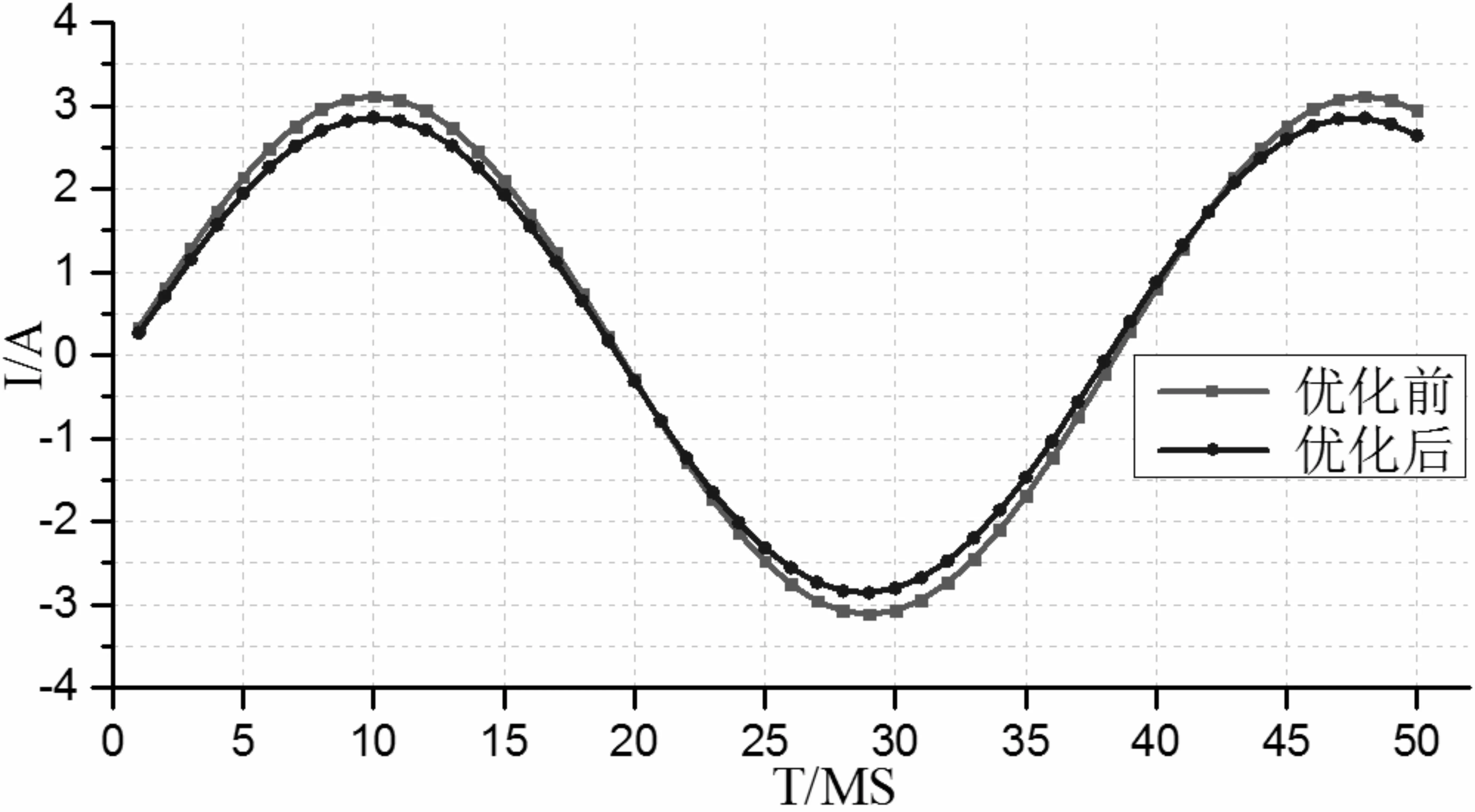
图8 电流曲线对比

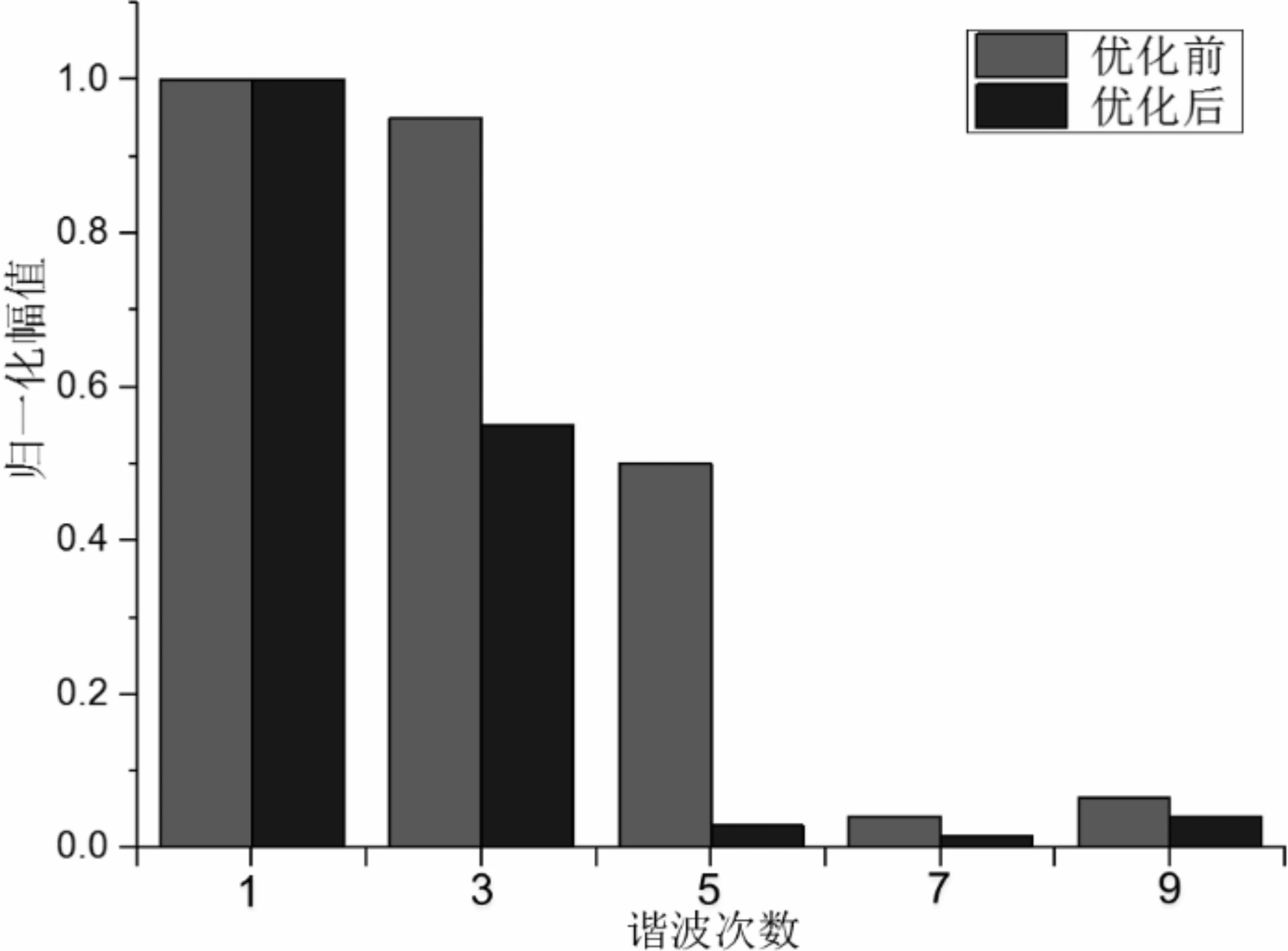
图9 空载反电动势谐波含量对比

通过表7可以得到，优化后的电机平均推力为40.04N,推力波动率为0.46%，峰值电流为2.74A，效率为35.36%，空载反电动势谐波畸变率为5.54%；通过极限学习机高精度建模优化后的电机，平均推力增大了46.24%，推力波动减小了71.78%，峰值电流减小了9.27%，效率增加了22.27%，空载反电动势减小了48.51%。表明经过ELM算法建模优化后的电机推力大、推力波动小、峰值电流小、效率高、谐波含量少，电机运行性能显著提升。

表7 电机性能参数对比

4 结 论

根据动圈式双次级永磁同步直线电机的结构特点，构建电机的有限元模型，采用多支持向量机建立快速计算模型，使得建模精度高达93%，引入粒子群算法对电机结构参数进行优化，得到一组最优的电机结构参数，建立相对应的有限元模型，进行仿真实验，实验结果表明优化后的具有推力波动小、推力大、电流小、谐波含量小，稳定性强、效率高等优点，达到了电机优化设计的目标。

[1] 韩雪岩，祁坤，张哲，等. 永磁同步直线电机磁阻力分析及抑制措施[J]. 电工技术学报, 2015， 30(6): 72-76.

[2] Isfahani A H, Ebrahimi B M, Lesani H. Design Optimization of a Low-Speed Single-Sided Linear Induction Motor for Improved Efficiency and Power Factor[J]. IEEE Transactions on Magnetics, 2008, 44(2):266-272.

[3] Lee D Y, Jung C G, Yoon K J, et al. A Study on the Efficiency Optimum Design of a Permanent Magnet Type Linear Synchronous Motor[J]. IEEE Transactions on Magnetics, 2005, 41(5):1860-1863.

[4] 赵吉文, 汪娅骅, 陈盼盼,等. 组合核函数多支持向量机的直线电机建模[J]. 电机与控制学报, 2014(2):90-95.

[5] 王群京, 鲍晓华, 倪有源,等. 基于支持向量机和遗传算法的爪极发电机建模及参数优化[J]. 电工技术学报, 2006, 21(4):57-61.

[6] 包广清, 郑文鹏. 基于正交设计和支持向量机的横磁通永磁电机参数优化[J]. 应用基础与工程科学学报, 2012, 20(5)：912-921.

[7] 杨维, 李歧强. 粒子群优化算法综述[J]. 中国工程学, 2004, 6(5):87-94.

[8] 夏永明, 付子义, 袁世鹰,等. 粒子群优化算法在直线感应电机优化设计中的应用[J]. 中小型电机, 2002, 29(6):14-16.

[9] 胡家声, 郭创新, 曹一家. 基于扩展粒子群优化算法的同步发电机参数辨识[J]. 电力系统自动化, 2004, 28(6):35-40.

[责任编辑：张永军]

Design Optimization of Permanent Magnet Synchronous Linear Motor Based on Multiple Support Vector Machine

XU Dao-ji

(Anhui Hongshi Optoelectronic Co.Ltd, Hefei 230601, China)

Multiple support vector machine (MSVM) was introduced to solve the rapid modeling problem of permanent magnet synchronous linear motor design optimization. After the analysis of 3D-FEA, using MSVM to map the relation of motor structure parameters and motor performances, building the rapid model for optimization calculation which can regress and predict the motor performances (thrust, thrust ripple, efficiency and harmonic distortion rate), the accuracy of this model built by MSVM can up to 93% and above;Particle Swarm Optimization (PSO) was introduced to optimize the MSVM motor model to get the motor best combination of structure parameters. After the simulation experiments based on FEA, the results indicate that: the PMSLM motor based on MSVM modeling optimization has high thrust, low thrust ripple, low peak current, high efficiency which can satisfy the demands of motor design optimization.

permanent magnet synchronous linear motor (PMSLM); multiple support vector machine (MSVM);thrust ripple; harmonic distortion rate;grey wolf algorithm (GWA)

2016-08-06

徐道际(1973—)，男，安徽合肥人，安徽宏实光机电高科有限公司工程师。

TM359.4

A

2096-2371(2016)04-0077-06