图形相似中的数学思想

文/朱广科

图形相似中的数学思想

图形相似是初中数学的重要内容.它包含着几种数学思想.现以2016年中考题为例,把图形相似的常见数学思想归纳如下,供你学习时参考.

一、方程思想

例1（2016年安顺卷）如图1，矩形EFGH内接于△ABC，且边FG在BC上，若AD⊥BC，BC=3，那么EH的长为．

解：疫四边形EFGH是矩形，亦EH∥BC，亦△AEH∽△ABC，

点评：根据相似三角形的性质得到对应边成比例，设未知数，利用比例式作为相等关系建立方程.

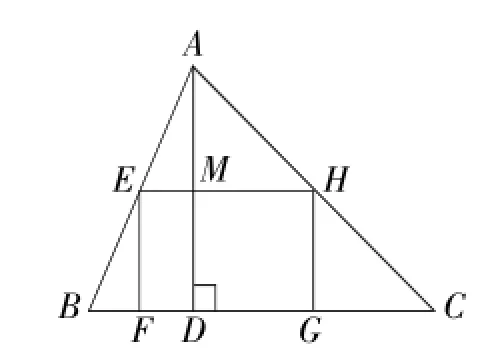
图1

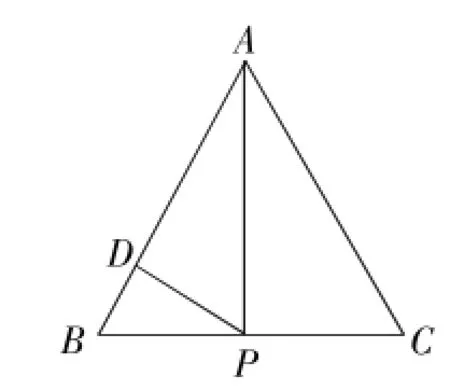
图2

二、函数思想

例2（2016年泰安卷）如图2，正△ABC的边长为4，点P为BC边上的任意一点（不与点B、C重合），且∠APD=60°，PD交AB于点D援设BP=x，BD=y，则y关于x的函数图象大致是（）

解：∵△ABC是正三角形，∴∠B=∠C=60°，

∵∠BPD+∠APD=∠C+∠CAP，∠APD=60°，∴∠BPD=∠CAP，

∴△BPD∽△CAP，亦BP∶AC=BD∶PC，

∵正△ABC的边长为4，BP=x，BD=y，

点评：利用相似三角形的性质建立了y与x的二次函数关系式，问题化难为易，要注意自变量的取值范围.

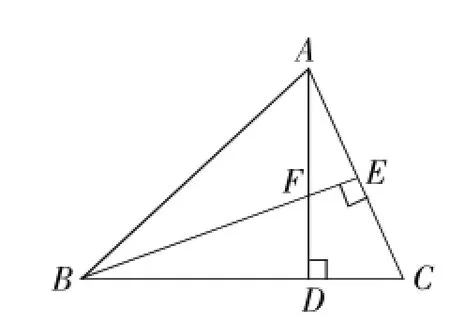
图3

三、转化思想

例3（2016年齐齐哈尔卷）如图3，在△ABC中，AD⊥BC，

BE⊥AC，垂足分别为D，E，AD与BE相交于点F援

（1）求证：△ACD∽△BFD；

（2）当tan∠ABD=1，AC=3时，求BF的长．

解：（1）证明：疫AD⊥BC，BE⊥AC，

亦∠BDF=∠ADC=∠BEC=90°，

∴∠C+∠DBF=90°，∠C+∠DAC=90°，∴∠DBF=∠DAC，

亦△ACD∽△BFD．

（2）∵tan∠ABD=1，∠ADB=90°，∴AD=BD，

又∵△ACD∽△BFD，亦△ACD≌△BFD，亦BF=AC=3．

点评：全等是特殊的相似，它的相似比是1，在相似问题中添加条件，可转化为全等问题求解.

四、分类讨论思想

例4（2016年河南卷）如图4，已知AD∥BC，AB⊥BC，AB=3，点E为射线BC上一个动点，连接AE，将△ABE沿AE折叠，点B落在点B忆处，过点B忆作AD的垂线，分别交AD，BC于点M，N援当点B忆为线段MN的一个三等分点时，BE的长为．

解：由翻折的性质，得AB=AB忆，BE=B忆E．

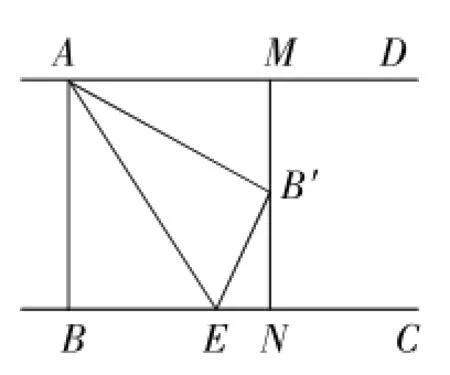
图4

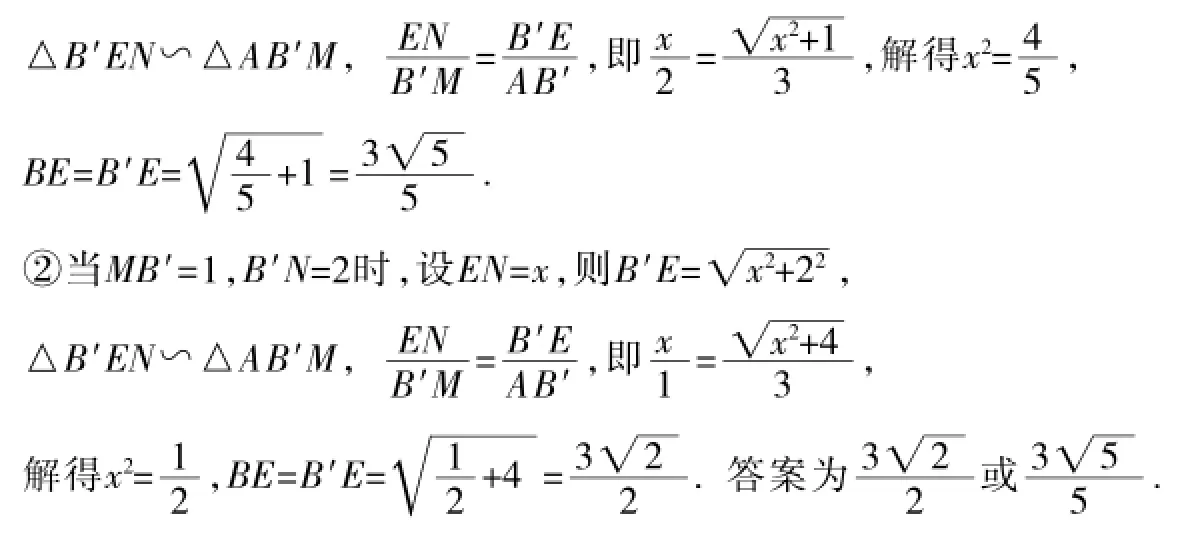
点评：当图形的形状或图形的位置不确定时，需分类讨论.本题由于三等分点的位置关系不确定，需要讨论，谨防漏解.

责任编辑：王二喜