地铁车辆基地出入线一度停车再起动的平纵断面关系模型

凌景文

(中铁第四勘察设计院集团有限公司城市轨道交通和地下工程设计研究院,430063,武汉∥工程师)



地铁车辆基地出入线一度停车再起动的平纵断面关系模型

凌景文

(中铁第四勘察设计院集团有限公司城市轨道交通和地下工程设计研究院,430063,武汉∥工程师)

从《地铁设计规范》相关条文规定出发,探讨车辆基地出入线列车一度停车再起动的平纵断面关系;分析列车在停车时、停车后和起动时等三种不同工况的受力情况。根据牵引计算原理,建立其平纵断面关系模型。以长沙市轨道交通2号线西延二期工程为例,计算出入线的最大坡度与最小曲线半径。

地铁； 车辆基地； 出入线; 一度停车; 平纵断面关系模型

Author′s address Design Institute of Urban Mass Transit and Underground Engineering,China Railway Siyuan Survey and Design Group Co.,Ltd.,430063,Wuhan,China

GB 50157—2013《地铁设计规范》6.4.2条规定:“出入线宜在车站端部接轨,并应具备一度停车再起动条件。”条文说明中对该规定进一步做了如下解释：“距离正线道岔警冲标之前,留有列车临时停车和再起动的地段,不小于一列车长度+安全距离。在隧道内,若进站为下坡,线路坡度不宜大于 24‰,并检验按 30～35 km/h 制动停车的安全保障;对于进站为上坡,原则上检验具备列车起动条件即可,但一般不宜大于 24‰,困难时不大于 30‰。”但其对一度停车再起动条件的计算公式并未做详细说明。

为了各地铁工程设计出合理的车辆基地出入线,避免工程浪费,并确保列车运行安全,参考铁路设置的进站缓坡及其计算方法[2]，本文对地铁车辆基地出入线一度停车再起动的平纵断面约束关系建立模型,为地铁工程设计者提供参考。

1 公式推导

一度停车再起动条件的计算包括了列车制动工况和列车牵引工况两个部分的计算。制动工况时,列车受力为运行阻力、附加阻力以及列车制动力;牵引工况时,列车受力为牵引力、运行阻力、起动阻力和附加阻力。本文不考虑风、雨、雪等环境条件对列车运行的影响，同时为方便计算,将列车简化为单质点模型[3]。

1.1 列车牵引力计算

本文以地铁B型车为例,采用4节动车和2节拖车的编组,为无级牵引。牵引力的取值有以下两种情况:

(1) 按列车牵引特性曲线取值,牵引力F是列车实际速度v的函数[4]。即：

F=f(v)

(1)

这种情况适用于有可用牵引曲线的场合。以长沙轨道交通2号线运营车辆为例，其牵引特性曲线如图1所示。

(2) 按加速度来计算牵引力,即根据列车当前速度以及列车在该点的目标速度来计算所需牵引力：

F=f(v,vt)

(2)

或

F=(MM+Mr)·a(v,vt)

(3)

式中:

vt——列车目标速度；

MM——列车中的动车总质量;

Mr——列车中的拖车总质量;

a(v,vt)——与列车实际速度、目标速度相关的加速度。

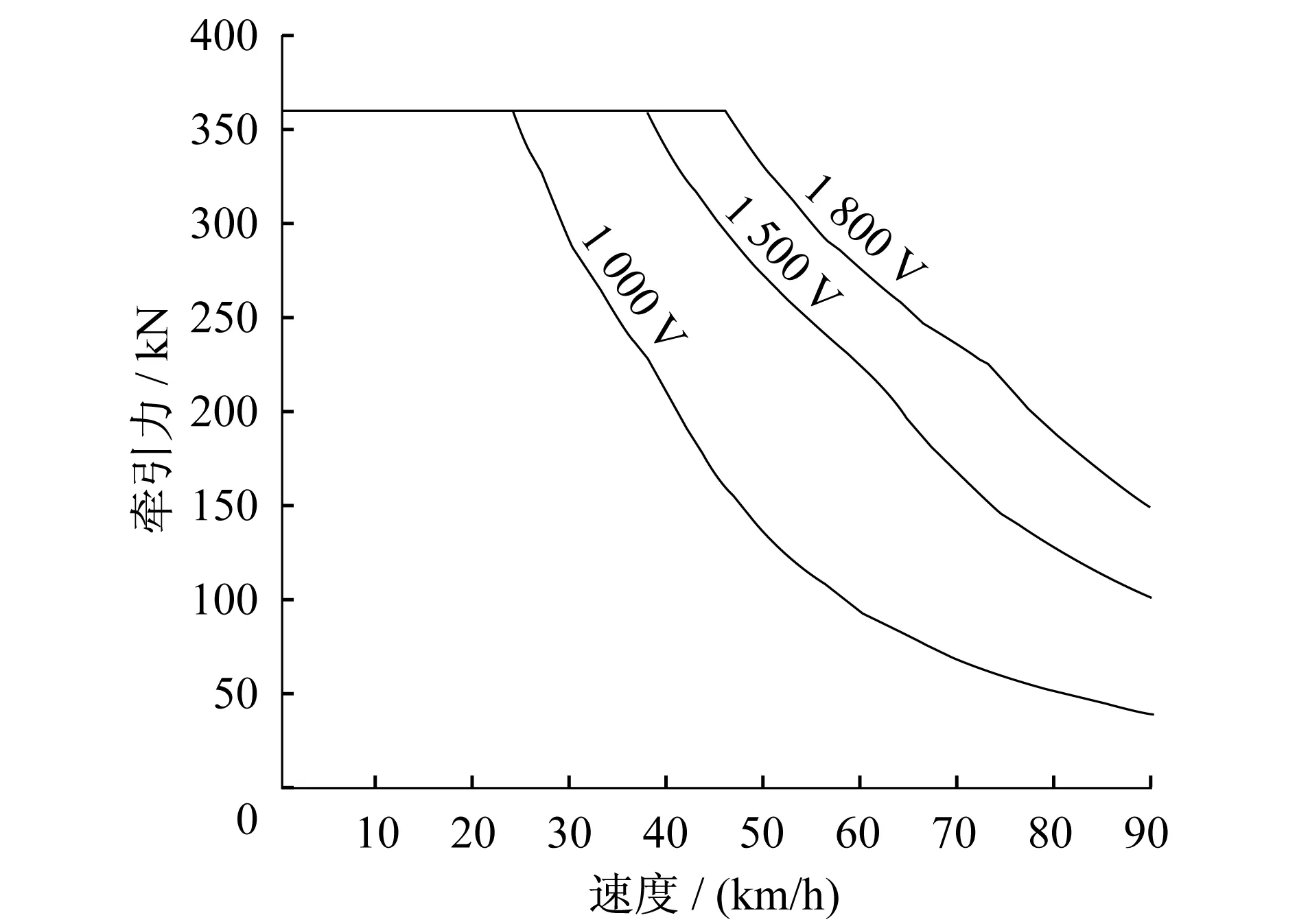
图1 长沙轨道交通2号线在空载条件下各种电网电压的列车牵引特性曲线

1.2 列车运行阻力计算

列车运行阻力可以分为机车阻力和车辆阻力。由于列车编组方式不一样,因此不同的列车有不同的阻力模型。

1.2.1 基本阻力

列车运行过程中,由于机械摩擦、空气摩擦等因素的作用而产生的固有阻力，称为列车的基本阻力。由于基本阻力中的有些因素不能通过定量的公式来计算,因此,一般通过大量的试验确定针对不同车型和编组的经验公式，来近似表达列车的基本阻力。根据《列车牵引计算规程》(以下简为《牵规》),列车基本阻力的计算公式[5]为:

w0=a+bv+cv2

(4)

式中：

w0——单位基本阻力；

a，b，c——与车辆有关的经验常数。

可针对不同的动车与列车编组,从生产厂家查定这些数据。

1.2.2 附加阻力

根据《牵规》有关坡道附加阻力的条款:机车、车辆的单位坡道附加阻力,其数值等于坡道坡度的千分数。即:

wi=i

(5)

式中:

wi——坡道附加阻力，N/kN；

i——坡度，‰。

列车在曲线上运行时,因摩擦等原因会产生曲线附加阻力。曲线附加阻力的大小和曲线半径、列车速度、曲线外轨超高以及轨距加宽等许多因素有关,很难用理论的方法推导出计算公式,一般采用如下的经验公式来计算：

(6)

式中：

wr——曲线附加阻力，N/kN；

A——经验常数；

R——曲线半径，m。

列车在隧道中运行会产生隧道附加阻力，其主要是指隧道中的空气不流通而产生的阻力。隧道附加阻力的大小与隧道长度、隧道截面积、列车截面积以及列车外形等有关。隧道越长,隧道附加阻力越大；列车越长、速度越高,隧道附加阻力也越大。当前,理论上计算隧道附加阻力尚不成熟,通常采用经验公式来计算[8]。即：

ws=0.000 13Ls

(7)

式中：

ws——隧道附加阻力，N/kN；

Ls——隧道长度，m。

因此,一般情况下,附加阻力wf的计算式为：

wf=wi+wr+ws

(8)

1.2.3 起动阻力

起动阻力wq随很多因素而变化,与车辆质量、外界条件等有很大的关系。目前，我国尚无地铁车辆起动阻力的试验资料,参照前苏联有关资料:

(9)

1.3 列车制动力计算

列车制动力是控制列车运行而人为施加的阻力，通常由列车上安装的制动装置产生。制动力的大小与列车运行速度、制动方式等因素有关。一般来讲,列车确定以后,制动力的计算仅与当前速度有关。即：

Fzd=f1(v)

(10)

式中：

Fzd——列车制动力，kN；

v——列车速度，km/h。

以长沙轨道交通2号线运营车辆为例,其列车制动特性曲线如图2所示。

图2 长沙轨道交通2号线电压1 500 V时列车制动特性曲线

1.4 列车一度停车和再起动受力模型

(1)一度停车时,列车为制动工况,其受力模型为:

F合=Fzd+wfMg

(11)

(12)

式中：

F合——列车所受合力；

M——列车总质量；

a——列车加速度。

将其简化为匀减速直线运动,列车制动距离为:

(13)

式中：

S——列车制动距离；

Lxj——信号机至警冲标之间的距离。

若S大于Lxj,则需增设安全线,从而增加工程投资。因此，本文采用不设置安全线的方法,将走行距离限制为不大于Lxj。Lxj的计算可参考文献[3]。

制动时出入线的平纵断面约束模型为:

(14)

(2)一度停车后,假设列车处在溜车的临界状态,分两种情况分析列车受力。

① 若不采用制动措施,此时列车受力为摩擦力、支撑力、重力,将3种力按垂直轨道方向分解,列车受力图如图3所示。其中,G为列车所受重力,G2为列车重力在平行坡道方向上的分力,G1为列车重力在垂直坡道方向上的分力。

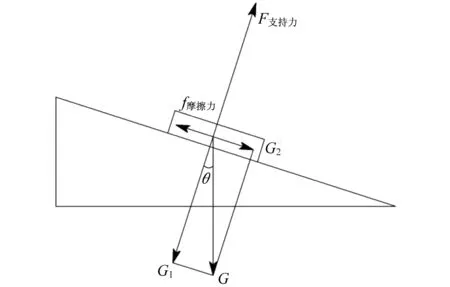
图3 坡道上列车不制动时的受力分析图

受力模型为:

f摩擦力≥G2

(15)

起动时,可假设摩擦力为最大静摩擦力(最大静摩擦力等于最大静摩擦系数与机车重力的乘积),即:

f摩擦力=μG1

(16)

式中：

μ——轮轨摩擦系数[7],约为0.001 98。

由于G2=Gsinθ,G1=Gcosθ=G(1-sin2θ)1/2,因此可求得:

(17)

此结论与《地铁设计规范》对停车线的要求一致。

② 若采用制动措施,此时列车受力为摩擦力、支撑力、重力、制动力,将4种力按垂直轨道方向分解,列车受力图如图4所示。

图4 坡道上列车制动时的受力分析图

受力模型为:

f摩擦力+Fzd≥G2

(18)

化简可得:

μMg cos θ+Fzd≥Mg sin θ

(19)

求得：

(20)

式中：

g——重力加速度。

由式(20)知，sinθ的上限值为Fzd取最大值时。Fzd最大值可查阅厂家相关资料取得。

(3) 再起动时,按一定的牵引质量计算列车起动模型，对列车质量的起动阻力加以修正后，得再起动地段的最大坡度为:

(21)

式中：

Fq——计算起动牵引力，kN；

λy——牵引力使用系数，λy=0.9。

2 计算实例

以长沙市轨道交通2号线西延二期为例,对上述模型作进一步分析与论证。2号线西延二期工程西起黄桥大道停车场(西端预留继续西延的工程条件,出入线南接黄桥停车场),止于西延一期工程梅溪湖西站,沿途设月季路站、松柏路站、看云路站、樱花路站、百合路站、金菊路站、映日路站，线路长约8.5 km。西延二期工程线路走向如图5所示。其中，月季路站为停车场出入线接轨站。接轨示意图如图6所示。

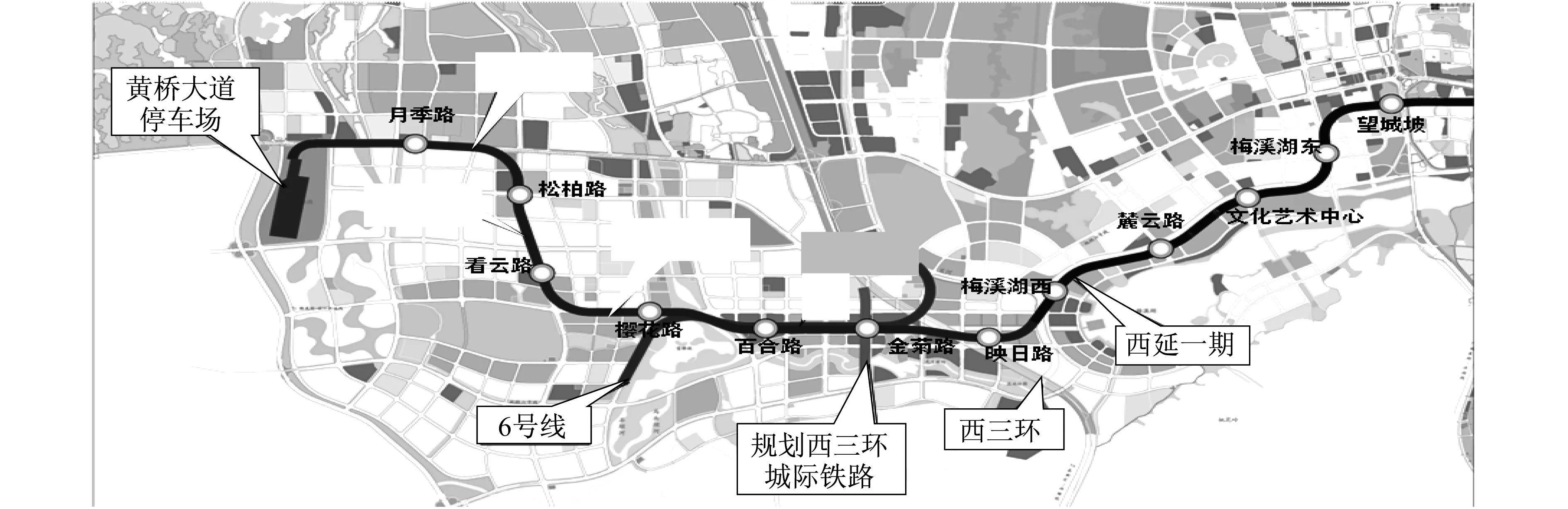
图5 长沙市轨道交通2号线西延二期线路走向示意图

图6 停车场出入线接轨示意图

列车空载时,总质量约为109 t,长为120 m,出场速度为35 km/h,查阅B型车牵引特性曲线和制动特性曲线可知,列车低于35 km/h,电压为1 500 V时,列车的牵引力为350 kN,制动力为335 kN,粘着系数为2.3%。隧道长度为500 m。

(1) 列车从出入线进入正线,若月季路站下行方向无法接车,则列车制动。其制动距离为:

(22)

由式(22)可得表1。表中空白处为S≤0或S≥Lxj,表示列车无法制动或无效制动。

由表1可知，列车在《地铁设计规范》规定的最大容许坡度范围内均能满足制动要求。

(2) 列车停车时,施加制动力后,最大下坡坡度为:

因此,最大坡度应小于24‰。

(3) 对列车一度停车后进行起动坡度检算。根据式(21)可以得出:

(23)

①R已知时,求i的上限值。

因i≤0(下坡)时列车肯定可以正常起动,不需进行起动坡度检算，故在此只需求出i的上限。由式(23)可求得:

i≤{-(5.06+415.8/R)+[(5.06+415.8/R)2+

1.2(355.6-415.8/R)]1/2}/0.6

(24)

由式(24)可以看出,i与R成正比,输入R可求得对应的i(见表2)。

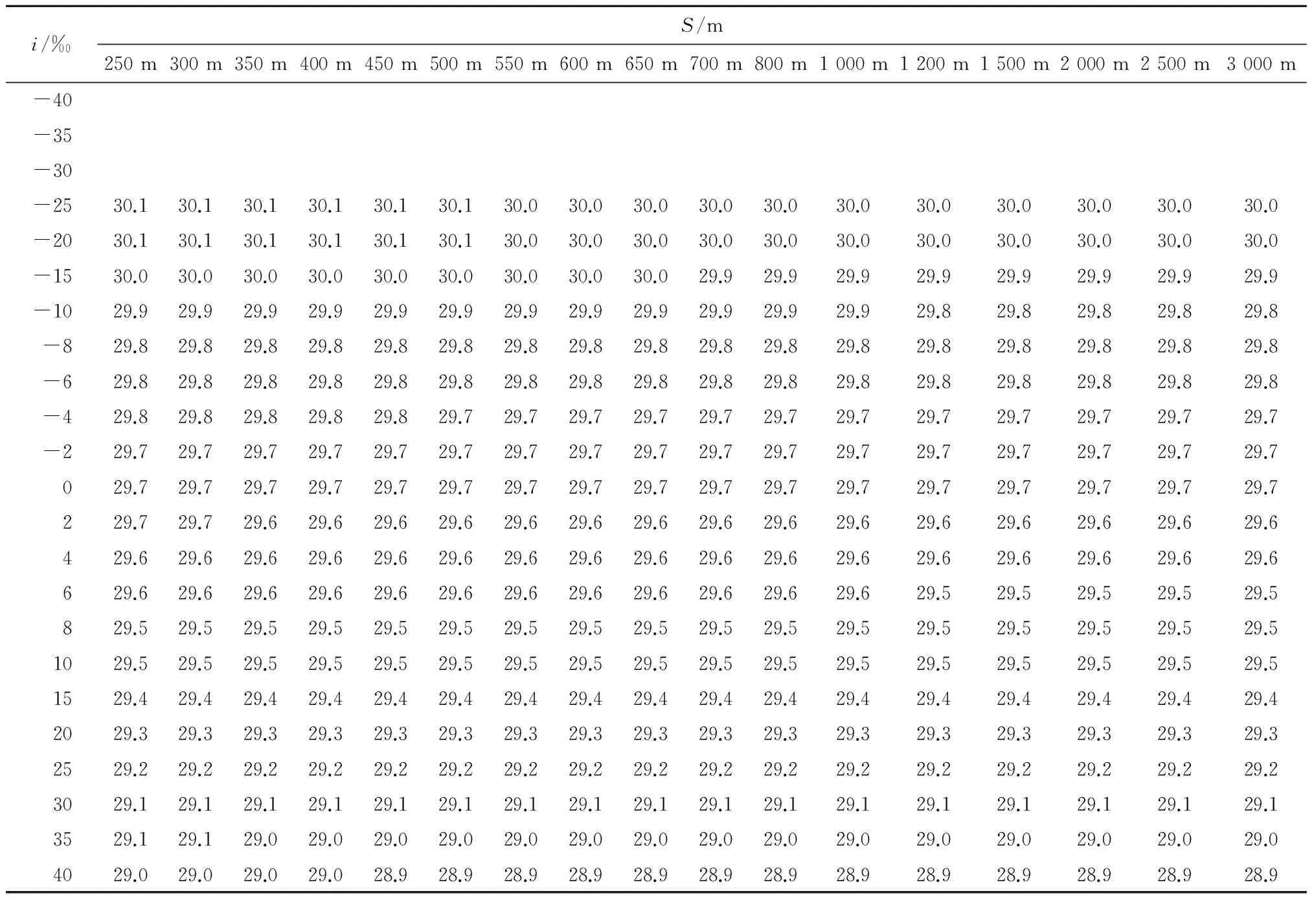
表1 不同曲线半径、坡度下的制动距离表

表2 R已知时的i最大值

②i已知时,求R的最小值。

由式(23)可求得:

(25)

i≤24‰，据此对R求最小值，如表3所示。

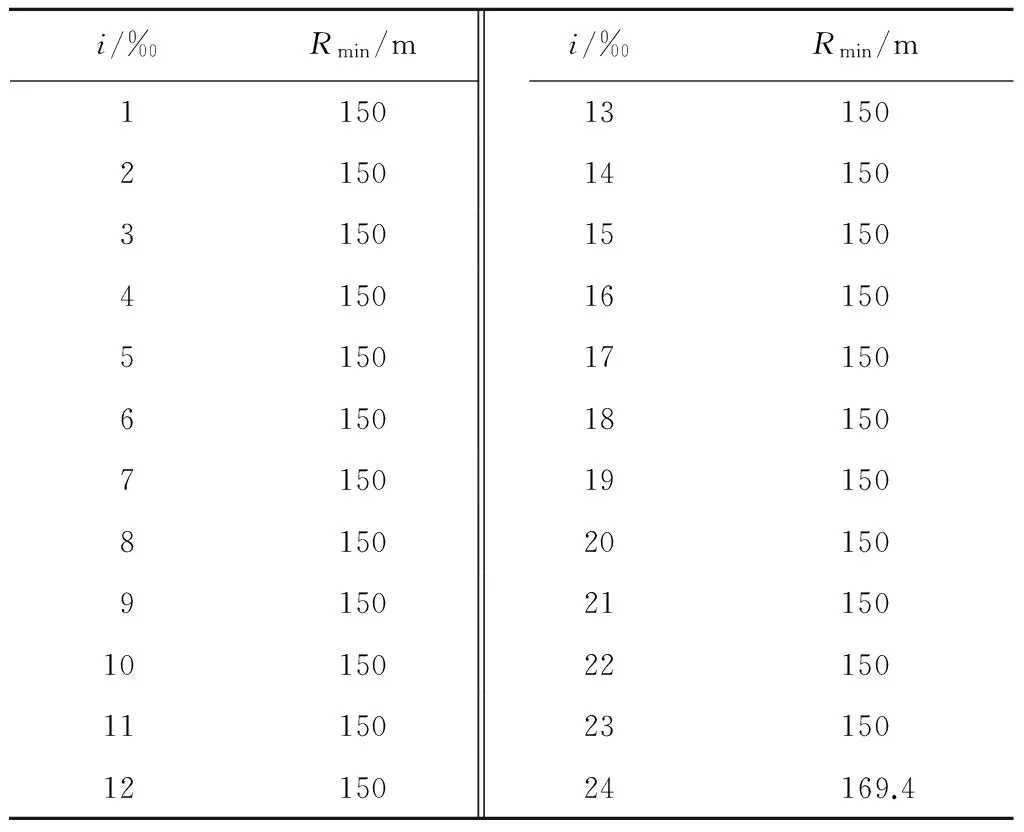
表3 i已知时的R最小值

3 结论

以长沙市轨道交通2号线西延二期为例验算,若进站为下坡,线路坡度不宜大于 24‰,能保障列车按 30～35 km/h 制动停车的安全,曲线半径对停车影响较小;若进站为上坡,经检验线路坡度≤24‰具备列车起动条件,曲线半径不宜小于200 m。

[1] 中华人民共和国住房和城乡建设部.地铁设计规范：GB 50517—2013[S].北京：中国建筑工业出版社，2013.

[2] 铁道第四勘测设计院.铁路工程设计技术手册——站场及枢纽[M].北京:中国铁道出版社,2004:36.

[3] 石红国,彭其渊,郭寒英.城市轨道交通牵引计算模型[J].交通运输工程学报,2005,5(4):20.

[4] 毛保华,姜帆,刘迁,等.城市轨道交通[M].北京:科学出版社,2001.

[5] 中华人民共和国铁道部.列车牵引计算规程：TB/T 1407—1998[S].北京：中国铁道出版社，1998.

[6] 兰淑桂,蔺增良,张鹏.地铁出入线一度停车制动距离计算公式[J].铁道工程学报,2010,139(4):87.

[7] 金学松,刘启跃.轮轨摩擦学[M].北京:人民铁道出版社,2004.

[8] 谢宏诚.城市轨道车辆牵引仿真研究[D].上海:同济大学控制科学与工程系,2006.

Relationship Model between Plane and Vertical Sections for Metro Train Temporary Stopping and Re-starting on Vehicle Depot Entering and Exiting Route

LING Jingwen

From the view of some provisions in “Metro Design Code”, the relationship between plane and vertical sections for metro train temporary stopping and re-starting on metro vehicle depot entering and exiting route are discussed, the force situation of three kinds of working condition, including the stopping, stopped and re-starting is analyzed. Then, according to the theory of traction calculation, a relationship model between the plane and vertical sections is established. Taking the west extension of Changsha metro Line 2 on the second phase for example, the maximum grade and the minimum curve radius on the entering and exiting route in metro vehicle depot are calculated.

metro; vehicle depot; entering and exiting route; temporary stopping; relationship model between plane and vertical sections

U 212.3

10.16037/j.1007-869x.2016.04.010

2014-05-08)