“等时圆”及其应用

王存贵

(秦皇岛市第一中学 河北 秦皇岛 066006)



“等时圆”及其应用

王存贵

(秦皇岛市第一中学 河北 秦皇岛 066006)

“等时圆”是高中物理的一个重要模型，本文先研究了“等时圆”模型的建立，接着让学生们体会如何自己构造“等时圆”，以加深对“等时圆”的理解．

等时圆 最高点 最低点 光滑

学生在学习到牛顿第二定律这一部分内容时，常常会碰到“等时圆”这一类型的题目，由于初学会对“等时圆”的认识不够深刻，经常会用错，可见“等时圆”在高中阶段是一种比较难的物理模型．所以我们有必要强化对“等时圆”基本规律的理解，这样才有利于提高同学们的解题能力，开阔视野，下面笔者就先介绍一下等时圆模型．

1 等时圆模型的建立

【例1】如图1所示，ad，bd，cd是竖直面内3根固定的光滑细杆，a，b，c，d 位于同一圆周上，a点为圆周的最高点，d点为最低点，每根杆上都套着一个小滑环(图中未画出)，3个滑环分别从a，b，c处释放(初速为零)，用 t1，t2，t3依次表示各滑环到达 d 所用的时间，则

图1

A.t1t2>t3

C.t3>t1>t2D. t1=t2=t3

解析：设圆环半径为R，杆与水平面的夹角为α，则杆长可表示2Rsin α，根据牛顿第二定律

mgsin α=ma

【练习1】

如图2所示，ab，ac，ad是竖直面内3根固定的光滑细杆，a，b，c，d 位于同一圆周上，a点为圆周的最高点，d点为最低点，每根杆上都套着一个小滑环(图中未画出)，3个滑环均从a处释放(初速为零)，用t1，t2，t3依次表示各滑环到达b，c，d 所用的时间，则

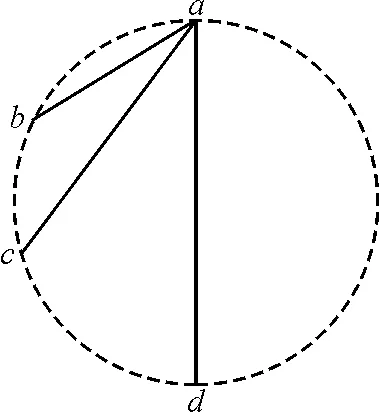
图2

A.t1t2>t3

C.t3>t1>t2D.t1=t2=t3

解析：设圆环半径为R，杆与水平面的夹角为α，则杆长可表示2Rsin α，根据牛顿第二定律

mgsin α=ma

2 构造等时圆

有时命题人为了增加题目的难度，不直接在题目当中给出等时圆，这时就需要同学们根据对等时圆的理解，自己构造出一个等时圆，来解决问题．

2.1 释放点在最高点的等时圆的构建

【例2】如图3(a)所示，光滑细杆BC，DC和AC分别构成矩形ABCD的两邻边和对角线，AC∶BC∶DC=5∶4∶3，AC杆竖直，各杆上分别套有一质点小球a，b，d，3小球的质量比为1∶2∶3，现让3小球同时从各杆的顶点由静止释放，不计空气阻力，则a，b，d 3小球在各杆上滑行的时间之比为

A．1∶1∶1 B．5∶4∶3

C．5∶8∶9 D．1∶2∶3

图3

解析：通过读题可知A，B，C，D 4点在以AC为直径的圆周上，圆在竖直平面内，A是圆的最高点．因此我们就能够以AC的中点O为圆心，OA为半径画出外接圆．如图3(b)所示，利用等时圆的结论，可知时间之比为1∶1∶1．所以A正确．

总结3：当题中没有直接给出等时圆时，需要我们自己去构造一个等时圆，并且要保证小球的释放点是圆的最高点，或者小球到达的最低点是圆的最低点．

【练习2】如图4(a)所示，AB和CD是两条光滑斜槽，它们各自的两端分别位于半径为R和r的两个相切的竖直圆上，并且斜槽都通过切点P，有一个小球由静止分别从A滑到B和从C滑到D，所用的时间分别为t1和t2，则t1和t2之比为

A.1∶1 B.1∶2

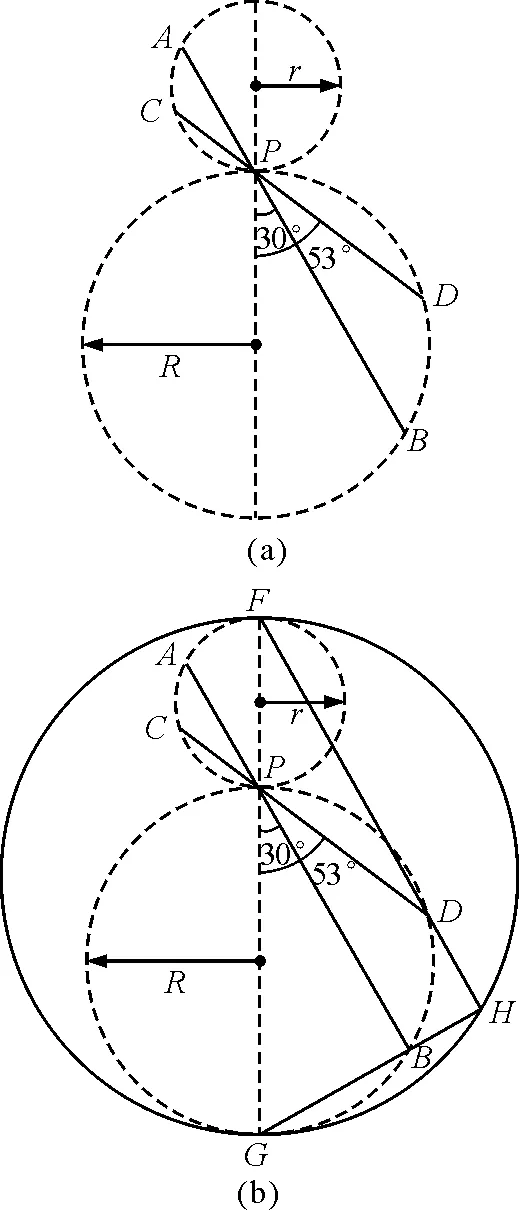
图4

解析：根据等时圆的结论很容易得出tAP=tCP，但是两个小球到达P点时，有速度，所以对PD和PB杆没有办法应用等时圆的结论来研究tPD和tPB的大小关系．

因此对沿AB槽下滑的小球应用牛顿第二定律和运动学公式来求小球下落的时间．

假设AB槽与竖直方向的夹角为α，AB=2(R+r)cos α

mgcos α=ma

可以得出

可见t与α无关，故下滑时间相同，即tAB=tCD．所以选A．

我们再对这个时间的表达式和这两个圆进行思考，大胆的猜想AB和CD槽是否也在同一个圆上，这个圆的半径为(R+r)．即AB和CD槽是这个外切圆的弦．

下面验证一下这个观点，做一个半径为(R+r)的圆，正好外切于大圆和小圆．小圆的最高点为F，连接AF，则AF与AB垂直，过F点做AB的平行线，与外切圆相交于H；大圆的最低点为G，连接GB，则GB与AB垂直，延长GB，交外切圆于H，GH与FH相垂直，ABHF构成了一个矩形，所以FH=AB．F，H，G 3点都在外切圆上，并且F是圆的最高点，因此可以应用等时圆的结论

tFH=tAB

所以

同理可证CD槽也是外切圆的一条弦．故下滑时间相同，即

tAB=tCD

【练习 3】如图5(a)是一倾角为α的输送带，A处为原料输入口，为避免粉尘飞扬，在A与输送带间建立一管道(假使光滑)，使原料从A处以最短的时间到达输送带上，则管道与竖直方向的夹角应为多大？

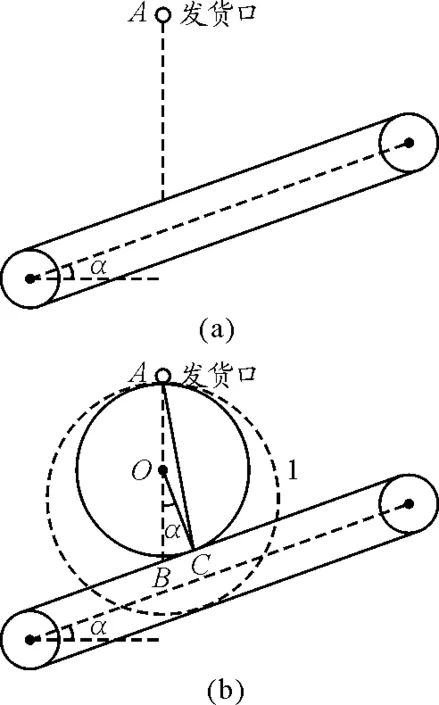
图5

2.2 释放点不在最高点的等时圆的构建

有时让我们研究时间问题时，会发现物体的释放点不在圆的最高点，所以这时题目当中给的不是等时圆，这个圆不能直接用，还需要我们自己以释放点为最高点来构造等时圆，通过例题3来讲解一下如何构造释放点不在最高点的等时圆．

【例3】如图6(a)所示，PA，PB，PC是竖直面内3根固定的光滑细杆，P，A，B，C位于同一圆周上，点D为圆周的最高点，C点为最低点．每根杆上都套着一个小滑环(图中未画出)，3个滑环分别从P处释放(初速为零)，用t1，t2，t3依次表示各滑环到达A，B，C所用的时间，则

A.t1t2>t3

C.t3>t1>t2D.t1=t2=t3

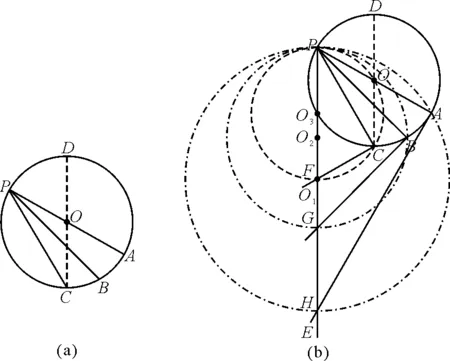
图6

总结4：释放点不在圆的最高点时，需要自己构造一个圆，这个圆以释放点为最高点，过所在轨道的最低点做垂线，垂线与释放点所在的竖直线会出现一个交点，释放点与交点之间的距离即为等时圆的直径，中点为轨道所在等时圆的圆心．也可以这样来构造等时圆，过轨道的中点做垂线，垂线与释放点所在竖直线会出现一个交点，交点即为轨道所在等时圆的圆心，释放点到交点的距离为等时圆的半径．

1 王睿峰. “等时圆”的基本规律及其应用. 物理通报，2012(02)：125～127

2 陈栋梁.“等时圆”的等时“原理”在物理问题解决中的妙用.物理教师，2013(03)：28

2016-01-06)