新型三自由度多连杆混合驱动机构的运动学分析和工作空间数值求解

朱凯君，蔡敢为，张 林，陈 渊，唐剑波

(1.广西制造系统与先进制造技术重点实验室 广西大学机械工程学院，广西 南宁 530004；2.山东交通大学工程机械学院，山东 济南 250357)



新型三自由度多连杆混合驱动机构的运动学分析和工作空间数值求解

朱凯君1，蔡敢为1，张 林2，陈 渊1，唐剑波1

(1.广西制造系统与先进制造技术重点实验室 广西大学机械工程学院，广西 南宁 530004；2.山东交通大学工程机械学院，山东 济南 250357)

可控机构是指单自由度机构中的某些结构运动参数或机构输入运动，和多自由度闭链机构中的某些运动可由微机进行实时控制，或以人工方式进行多个固定位置的控制，以达到柔性输出、改善机构的运动学和动力学特性的目的。基于可控机构理论提出了一种新型三自由度多连杆混合驱动可控机构，并使用Newton-Raphson法对该混合驱动机构进行运动学建模，得到该混合驱动机构的正逆解，然后对该可控机构正解进行了数值求解，最后利用运动学正解和奇异性判断条件在MATLAB软件中进行程序编写，得到该可控机构主要工作空间参数，并且绘制了工作空间示意图。其结果显示该混合驱动机构不仅具有灵活度高、微机实时控制、柔性化输出的优点，而且工作空间符合挖掘作业要求，在工程上具有一定的实用性。本研究为该混合驱动机构后续的动力学分析和控制系统设计提供了基础。

可控机构；混合驱动机构；Newton-Raphson法；运动学正逆解；工作空间

0 前言

混合驱动机构[1]是可控机构[2]的一个分类，同时采用了常用电机(不可控电机)和伺服电机(适时可控电机)作为动力源。混合驱动机构的概念是在20世纪90年代初由Tokuz[3]首次提出，经历了20多年的发展研究，各国学者在各个方面对其进行了深入地研究，取得了很多重要的研究成果。

运动学分析[4]是混合驱动机构设计的主要问题之一，包括了工作空间、奇异性、运动学设计等方面，于洪英[5]等推导了五杆机构的运动学正解和运动学逆解方程，并基于Kane动力学方程，对五杆机构进行了动力学分析；王进戈[6]等基于求坐标推导出了具有两自由度特征的球面五杆机构的速度方程和雅可比矩阵的解析表达式，研究了球面五杆机构奇异位形及其灵活度；邓嘉鸣[7]等研究一种双滑块驱动的平面五杆机构及其运动特征，并且分析了机构末端操作点运动在不同轨迹时两滑块驱动的运动规律及特性；Li[8]等对混合驱动七杆机构的运动规律进行了研究，通过仿真建模分析了混合驱动七杆机构的工作。

1 新型混合驱动机构构型

基于可控机构理论[9]，设计出一种新型三自由度多连杆混合驱动机构。如图1所示，第一主动杆和第二主动杆由伺服电机驱动，可通过微机编程进行实时控制，并且将电机和减速器全部安装在机架上，减小了动臂、斗杆的转动惯量，具有良好的动力学特性，并且使用了两个四杆机构来控制小臂，且将其中一个杆件安装在大臂上，可以保证满足各机构奇异性[10]的前提下，使该混合驱动机构具有较大的工作空间。

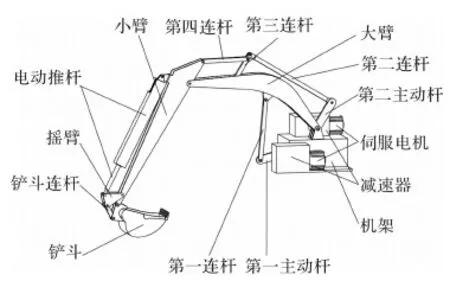
图1 新型三自由度多连杆混合驱动机构三维模型图Fig.1 3-D model of a novel 3-DOF multi-link hybrid driving mechanism

2 混合驱动机构的运动学分析

2.1 混合驱动机构的运动学建模

连杆机构运动学分析方法主要有解析法和数值法[11]，数值法相比于解析法，其优点在于可以高效率的求解杆件数量多、结构复杂的机构以及耦合度高、非线性的运动模型[12]，所以本文利用Newton-Raphson数值算法[13]建立该混合驱动机构的运动学模型。

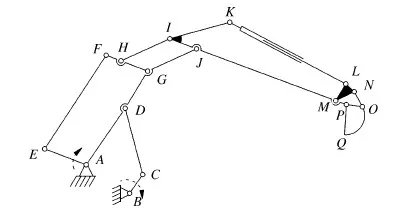
图2 混合驱动机构的机构简图Fig.2 Schematic diagram of hybrid driving mechanism

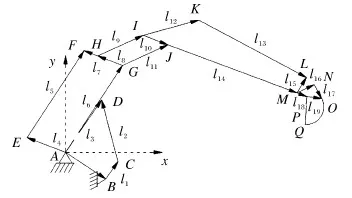
图3 混合驱动机构矢量图Fig.3 Vector diagram of hybrid driving mechanism

将这些矢量关系式展开，可以得到

(1)

(2)

(3)

(4)

(5)

2.2 混合驱动机构位姿的运动学正解

在该混合驱动机构中，主动杆为第一主动杆、第二主动杆和电动推杆，输出机构为挖掘机大臂、小臂和铲斗，故该混合驱动机构位姿的运动学正解可描述为：已知机构中各构件的尺寸长度li(i=1,2,…,19)，机架铰点的位置xB,yB，给定第一主动杆输入角φ1和第二主动杆输入角φ4以及电动推杆的长度l13，求解机构中大臂位置角θ1、小杆的位置角θ2以及铲斗角位置角θ3和铲斗顶点的坐标xQ,yQ。

如图所示，根据正解的已知条件，对式(1)～(5)中所含的待求参数进行分析：

(1)在式(1)中，位置角φ1为已知参数，位置角φ2,φ3为待求参数；

(2)在式(2)中，位置角φ4为已知参数，且位置角φ6=φ3+∠GAD也为已知参数，则位置角φ5,φ7为待求参数；

(3)在式(3)中，位置角φ8=φ7为已知参数，且位置角φ11=φ3+π-∠JDA-∠DJG也为已知参数，位置角φ9,φ10为待求参数；

(4)在式(4)中，位置角φ14=φ10，且位置角φ12=φ10+∠KIM为已知参数，位置角φ13,φ15为待求参数；

(5)在式(4)中，位置角φ18=φ10，且位置角φ16=φ15-∠LMN为已知参数，位置角φ17,φ19为待求参数。

通过上述分析可得到所有待求参数：φ2,φ3,φ5,φ7,φ9,φ10,φ13,φ15,φ17,φ19，将所述上式整理成关于这些待求参数的10维非线性方程组。即

(6)

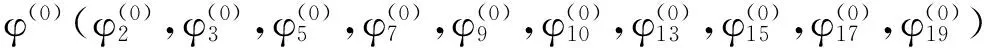
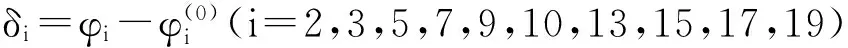
(7)

写成矩阵形式

JPδ=F

(8)

其中，

(9)

(10)

(11)

a1,1=-l2sinφ2,a1,2=-l3sinφ3

a2,1=l2cosφ2,a2,2=l3sinφ3

a3,2=l6sin(φ3+∠GAD),a3,3=-l5sinφ5,a3,4=l7sinφ7

a4,2=-l6cos(φ3+∠GAD),a4,3=l5cosφ5,a4,4=-l7cosφ7

a5,2=l11sin(φ3+π-∠JDA-∠DJG),a5,4=-l8sinφ7，a5,5=-l9sinφ9,a5,6=-l10sinφ10

a6,2=-l11cos(φ3+π-∠JDA-∠DJG)，a6,4=l8cosφ7,a6,5=l9cosφ9,a6,6=l10cosφ10

a7,6=-l12sin(φ10+∠KIJ)+l14sinφ10，a7,7=-l13sinφ13,a7,8=-l15sinφ15

a8,6=l12cos(φ10+∠KIJ)-l14cosφ10，a8,7=l13cosφ13,a8,8=l15cosφ15

a9,6=l18sinφ10，a9,8=-l16sin(φ15-∠MLN),a9,9=-l17sinφ17,a9,10=l19sinφ19

a10,6=-l18cosφ10,a10,8=l16cos(φ15-∠MLN),a10,9=l17cosφ17,a10,10=l19cosφ19

上式中的矩阵J为一阶偏导数矩阵，又称Jacobian矩阵，矩阵δ为校正矢量。将式(8)两边同乘以J-1，可得

δ=J-1F

(12)

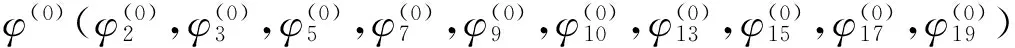
φ(1)=φ(0)+δ

(13)

由此得到了迭代方程

φ(k+1)=φ(k)+δ(k)+δ(k)(k=1,2,3,…)

(14)

直到|δ(k)|≤ε，其中ε表示收敛精度。当经过k次迭代后，得到的校正矢量的模小于收敛进度ε时，即得到的φ(k+1)为满足精度要求的非线性方程(2～6)的数值解。则挖掘机构动臂位置角θ1、斗杆位置角θ2、铲斗的位置角θ3，以及铲斗齿尖的坐标可由下式得出

(15)

2.3 混合驱动机构位姿的运动学逆解

混合驱动机构位姿的运动学逆解是正解的逆向过程，故其位姿的运动学逆解可描述为：给定大臂、小臂和铲斗的位置角位参数θ1,θ2,θ3，求解第一主动杆位置角φ1、第二主动杆位置角φ4以及电动推杆的长度 。

由式(15)可得：

(16)

联立式(1)～(5)与(16)。

根据逆解的已知条件，对式(1)至(5)中所含的待求参数进行分析，可得到上式中所有待求参数：φ1,φ2,φ4,φ5,φ8,φ9,φ13,φ16,φ17,l13，且有

φ6=φ3+∠GAD,φ7=φ8，φ11=φ3+π-∠JDA-∠DJG,φ12=φ10+∠KIM，φ14=φ10,φ15=φ16+∠LMN,φ18=φ10

将所述上式整理成关于这些待求参数的10维非线性方程组

(17)

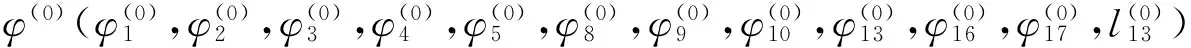
J1δ=F

(18)

其中

(19)

(20)

(21)

a1,1=-l1sinφ1,a1,2=-l2sinφ2

a2,1=l1cosφ1,a2,2=l2cosφ2

a3,3=-l4sinφ4,a3,4=-l5sinφ5，a3,5=l7sinφ8

a4,3=l4cosφ4，a4,4=l5cosφ5,a4,5=-l7cosφ8

a5,5=-l8sinφ8,a5,6=-l9sinφ9

a6,5=l8cosφ8,a6,6=l9cosφ9

a7,7=-l13sinφ13,a7,8=l15sin(φ16+∠LMN)，a7,10=cosφ13

a8,7=l13cosφ13,a8,8=-l15cos(φ16+∠LMN),a8,10=sinφ13

a9,8=-l16sinφ16,a9,9=-l17sinφ17

a10,8=l16cosφ16,a10,9=l17cosφ17

根据正解过程中的数值算法，即可求出φ(φ1,φ2,φ4,φ5,φ8,φ9,φ3,φ16,φ17,l13,)满足精度要求ε的数值解，进而得到第一主动杆位置角φ1、第二主动杆位置角φ4以及电动推杆长度l13。

3 混合驱动机构工作空间数值求解

工作空间[14]是机构的工作区域，是衡量机构性能和实用性的重要指标。在该混合驱动机构中，输出的构件是铲斗，故可用铲斗顶点Q的可达区域当作该混合驱动机构的工作空间。

从图2所示的机构简图可以看出各个杆件之间的容易发生奇异性的位置，如图3所示的机构矢量图所示，机架铰点B点在的坐标为：xB=100 mm，yB=-300 mm,大臂长度：LAJ=1 600 mm，小臂长度：LJN=1 000 mm，铲斗长度：LNQ=450 mm，如表1所示的各构件尺寸参数，并基于所得到的运动学正解并添加奇异性判断条件编写MATLAB程序[15]，可以求出Q点的可达区域，得到该混合驱动机构工作空间的主要参数，如表2所示，以及工作空间示意图，如图4所示。

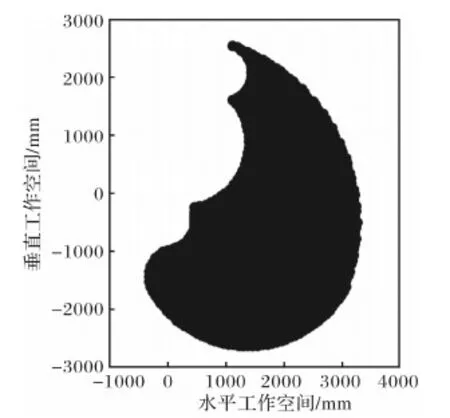
图4 混合驱动机构工作空间示意图Fig.4 Sketch diagram of hybrid driving mechanism’s working space

杆件l1l2l3l4l5l6l7l8l9杆长/mm2508007202508008002503501000构件l10l11l12l14l15l16l17l18l19杆长3501003201250170180150100130

表2 混合驱动机构工作空间的主要参数

4 结束语

本文基于可控机构理论提出了一种新型三自由度多连杆混合驱动机构，基于Newton-Raphson法对该混合驱动机构进行运动学位姿分析，得到了其运动学的正逆解，在其正解结果的基础上，添加机构奇异性的判断条件，用MATLAB软件对其进行了程序编写，得到了该机构工作空间的主要参数，并且绘制工作空间示意图，由此可知该机构可以应用在挖掘作业上，验证了该混合驱动机构在工程上的实用性。

[1] 张新华,张策,田汉民,混合驱动机构的创新设计及其应用[J].机械设计与研究,2001(9).

[2] 邹慧君, 李瑞琴, 郭伟忠,等.机构学10年来主要研究成果和发展展望[J].机械工程学报,2003,39(12):22-30.

[3]TokuzLC.Hybridmachinemodelingandcontrol[D].UK:LiverpoolPolytechnicUniversity,Ph.D.Dissertation,1992.

[4] 李瑞琴,郭为忠.现代机构学理论与应用研究进展[M].高等教育出版社,2014:335.

[5] 于洪英,唐德威,王建宇.平面五杆机构运动学的动力学特性分析[J].哈尔滨工业大学学报,2007,39(6):940-943.

[6] 王进戈,张均富,王强,等.球面五杆机构的运动学与性能分析[J].机械工程学报,2006,44(8):33-39.

[7] 邓嘉鸣,丁磊,沈惠平,等.双滑块驱动2自由度五杆机构的运动特性分析[J].机械设计,2011,28(8):38-42.

[8]LiRuiqin,DaiJS.Workspaceatlasandstrokeanalysisofseven-barmechanismswiththetranslation-output[J].MechanismandMachineTheory, 2013,47(1):117-134.

[9] 周洪.可控机构的设计理论及其应用研究[D].上海:上海交通大学,2000.

[10]周双林,姚燕安,郭为忠,等.混合输入五杆机构的奇异性分析[J].上海交通大学学报,2001,35(12).

[11]黎健玲,简金宝,李群宏,等.数值分析与实验[M].北京:科学出版社,2012.

[12]C.B.Garcia,W.I.Zhangwill.GlobalContinuationMethodsforFindingAllSolutiontoPolynomialSystemofEquationinNVariables[J].CenterforMathsStudiesinBusinessandEconomicsReportNo.7755,Univ.ofChicago,1997.

[13]王芳,赵美宁,王立党.基于牛顿-拉夫森数值算法的杆机构位置求解[J].西安工业学院学报,2005,25(3),220-222.

[14]周兵,毛泰祥,杨汝清. 3自由度RPS并联机构工作空间分析[J].湖南大学大学学报(自然科学版),2003(2).

[15]王小玉.MATLAB计算方法[M].北京:清华大学出版社,2012(10).

Kinematic analysis and working space numerical solution of a novel three degree of multi-link hybrid-driven mechanism

ZHU Kai-jun1, CAI Gan-wei2, ZHANG Lin1, CHEN Yuan1, TANG Jian-bo1

(1.Guangxi Key Laboratory of Manufacturing System & Advanced Manufacturing Technology, College of Mechanical Engineering of Guangxi University, Nanning 530004, China; 2.College of Engineering Machinery of Shandong Jiaotong University, Jinan 250357, China)

Controllable mechanism refers to a single degree of freedom mechanism with some structures’ motion parameters or input motion, and multi-degree of freedom linkage mechanism with some motion can be real-time controlled by computer or multiple fixed position be controlled by hand, in order to get flexible output and improve the kinematic and dynamic characteristics of mechanism. According to the controllable mechanism theory, a novel three degree of multi-link hybrid-driven mechanism was developed , and established the kinematic model of hybrid-driven mechanism based on Newton-Raphson method, and obtained the forward and inverse solution of hybrid-driven mechanism’s position, and numerical solution of the forward solution. According to the kinematic forward solution and the singularity judgment condition, the program was wrote in MATLAB, then obtained the working space main parameters and sketch map of hybrid-driven mechanism. The results show the hybrid-driven mechanism is favorable flexible, all-time control, flexible output and practicable, and the working space meets mining operation. This study provides a basis for the subsequent dynamic analysis and control system designing of the hybrid-driven mechanism.

controllable mechanism; hybrid-driven mechanism; Newton-Raphson method; kinematic forward and inverse solution; working space

2016-03-04；

2016-04-17

国家自然科学基金项目(51075077)

朱凯君(1990-)，男，广西大学机械工程学院硕士研究生。

TH112.2

A

1001-196X(2016)05-0061-07