轴向载荷作用下H形悬臂梁稳定性能研究
王文浩,苟文选,杨 帆,闫五柱
(1.西北工业大学力学与土木建筑学院,陕西 西安 710129;2.太原科技大学机械工程学院,山西 太原 030024)
轴向载荷作用下H形悬臂梁稳定性能研究
王文浩1,2,苟文选1,杨 帆1,闫五柱1
(1.西北工业大学力学与土木建筑学院,陕西 西安 710129;2.太原科技大学机械工程学院,山西 太原 030024)
受压的H形截面梁或柱是机械设备中普遍采用的结构构件,对其承载力的准确预测有重要的意义。本文采用解析法和有限元分析方法,分别计算了屈曲临界载荷和考虑初始缺陷的后屈曲承载力。通过分析得出主要结论:第一,考虑初始缺陷的后屈曲分析结果比较接近实际情况,与不考虑初始缺陷的临界载荷相比更接近规范计算值。第二,适用于欧拉公式的细长压杆屈曲后强度不会提高,因此屈曲后强度不能提供安全储备。第三,有限元解与规范计算值的差别是由于规范值考虑了安全系数。本文得出的结论可供机械工程设计人员参考。
悬臂梁;屈曲;后屈曲
0 前言
H形梁、柱和工字形梁结构广泛应用于重型机械行业中[1],如龙门架、架桥机、塔式起重机、桅杆起重机以及轨道的主要结构部件,桥式起重机主梁,桁架式起重机上下弦杆,门式起重机支腿以及振动设备底座[2]等。其中H形截面由于沿两主轴方向的截面抗弯模量比较接近,主要用于受压构件和沿两个主轴平面受弯的构件;工字形截面由于截面较高,一般仅用于在其腹板平面内受弯的构件。然而在实际工程中,纯粹的受压或者受弯构件是很少见的,因此工字梁也有受压的要求。作为机械工程主要结构的受压梁和柱主要工作在弹性阶段,因此基于线弹性理论的受压杆屈曲临界载荷分析比较常见,基于大变形理论的几何非线性和材料非线性后屈曲分析较为少见。但由于工程机械本身的工作特点,如露天作业多、超载时有发生以及工作环境的复杂性,大型工程机械在工作状态或非工作状态下可能会遭受到强风,地震,山洪,地质滑坡等超过工作载荷,使其结构应力超过弹性极限的载荷作用。2008年5月12日,四川汶川8.0级强震波及西安,全市1200多台塔吊,30%塔吊不同程度出现了故障和损坏而被迫停用,其中使用高度较高的20台塔吊受到严重损坏[3-4]。可见为机械结构的关键承力部件保留一定的安全储备是非常有必要的。由于钢结构通常具有较好的塑性变形能力[5],通过设计达到一定的安全储备是可行的[6]。本文以一普通H形梁为例,分析了在轴向压缩载荷作用下的屈曲性能,作为安全储备,对后屈曲性能也进行了相应的分析。
1 问题描述
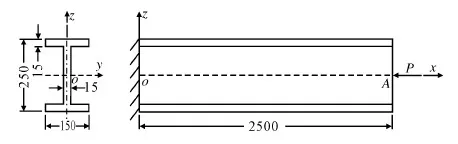
图1 H形截面悬臂梁Fig.1 H-section cantilever beam
本文建立的H形悬臂梁,为工程机械中常用的H形梁,其长度、截面尺寸、受力形式和约束情况如图1所示,坐标系采用笛卡尔固定坐标系,服从右手螺旋法则,左端为固定端,右端为自由端。梁材料采用普通碳素钢Q235钢,弹性模量E=206 GPa,泊松比μ=0.3,密度ρ=7.85 g/mm3。载荷P作用于A点,沿梁轴线方向作用,当P达到某一值时候,梁发生屈曲,该梁是否具有更高的后屈曲强度,尚需进一步判断。由实际情况可知,任何力都应作用在一定的分布面积上,A点作用的集中载荷P与实际情况不符,根据弹性力学[7]圣维南原理集中力P会对梁端部的局部区域内产生与均匀作用的分布力不同的效果,但是在离端部较远的区域内这种影响可以忽略不计。据此以集中力代替分布力不会对屈曲形式及承载力有显著影响。 目前预测构件屈曲载荷及后屈曲强度这类问题的方法主要有解析法和数值法。解析方法包括能求出精确解的解析方法和建立在一定的假设条件和适当简化基础上的工程算法,规范往往采用后者。数值方法目前较多采用商业有限元软件进行计算。下面将采用以上方法进行分析。
2 精确解析方法
该方法采用材料力学中分析压杆稳定性能的原理,先进行失稳类型的判断,然后确定计算方法,经过判断如果属于细长杆受压,可以直接采用欧拉公式[8]计算得到精确解析结果(以下简称解析解)。
首先计算基本的几何参数。横截面形心主轴最小惯性矩
横截面面积
A=150×250-(150-15)×
(250-15×2)=7 800mm2
横截面最小惯性半径
失稳类型的判断。根据文献[9],计算压杆的柔度值。
(1)
式中,λ为压杆的柔度或长细比;μ为压杆的长度因数,本文H形梁为悬臂梁,这里取2.0;l为压杆的几何长度;i为横截面最小惯性半径。
将以上计算结果代入式(1)得
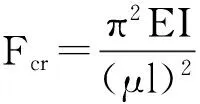
根据杆件稳定性理论,细长压杆失稳后承载力不能进一步增加。对于考虑初始缺陷的后屈曲计算目前尚没有精确地解析方法。
3 数值分析
本文采用有限元软件ANSYS和ABAQUS进行分析,为减少文字冗余,具体过程描述以ANSYS为例,对ABAQUS只将计算结果列出。
3.1 有限元模型建立
本文采用梁单元来模拟H形悬臂梁,梁单元采用精度较高的三节点beam189单元。沿梁长度方向划分10个单元,网格大小为250mm,单元共计10个,节点20个。通过收敛性检查10个单元所得结果是足够精确的。建立的有限元模型如图2所示。

图2 H形悬臂梁有限元模型Fig.2 FEM model of H-section cantilever
3.1.1 定义材料属性
本文选用H形悬臂梁材料密度为7.85g/cm3, 弹性模量为2.06E+5Mp, 泊松比为0.2,,用如下ANSYS命令定义材料属性:mp,dens,1,7.85e3 ;mp,ex,1,2.06e11;mp,nuxy,1,0.2。
3.1.2 施加载荷和边界条件
在有限元模型梁的右端A点施加集中力P=1 MN,在梁的左端施加固定端约束,A端自由,如图3所示。

图3 H形悬臂梁有限元载荷及约束条件Fig.3 FEM load and constraint condition of H-section cantilever beam
3.2 有限元分析
本文首先对H形悬臂梁进行屈曲模态计算即计算其临界力。然后进行后屈曲分析计算其屈曲后强度。
3.2.1 临界载荷
ANSYS中进行屈曲分析过程与ABAQUS中不同,不能直接进行屈曲计算,需要先进行静力分析,然后再进行模态计算。
在有限元模型建完后,先输入命令
antype,0
solve
进行求解完成静力计算,然后,输入命令
antype,1
bucopt,lanb,2,0
solve
求解屈曲模态,提取前两阶模态。
通过有限元分析计算得到H形悬臂梁的屈曲模态如图4所示。从图中可以看出第二阶屈曲模态的屈曲因子大约是第1阶模态的屈曲因子的7倍,所以第2阶模态及以后的模态所占比重很小,发生的可能性很小,实际的屈曲模态应与第1阶模态比较接近,以第1阶屈曲模态作为H形悬臂梁的临界失稳模态。计算得屈曲载荷为

图4 H形悬臂梁屈曲模态Fig.4 buckling mode of H-section cantilever beam
3.2.2 后屈曲载荷
后屈曲分析是在屈曲模态分析的基础上,在上文计算出的第1阶模态变形的基础上乘以一个缩放系数(2阶以上模态产生的影响忽略不计),叠加到原结构的每一个坐标点上,作为结构的位移初始扰动[10]。这个初始扰动也称为初始偏心,以此来代表本文H形梁的初始缺陷,此处初始偏心取H形梁截面较小尺寸的5%,即:150×5%=7.5 mm,考虑尚有安装偏差、构件加工误差等其它因素,将其一并计入初始偏心距中,故取为10 mm,缩放系数取0.01,相当于梁的最大偏移值为10 mm。然后去掉原模型上的力,施加新的载荷进行非线性迭代计算,直到收敛。
后屈曲分析中主要的设置包括首先使用命令nlgeom,1打开大变形,然后进行弧长法设置和弧长法终止准则:
arclen,1
arctrm,l
进行载荷子步设置
nsubst,200,,,1
提交ANSYS计算
solve.
最后得ANSYS计算结果是:
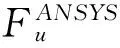
ABAQUS计算结果是:
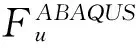
得出载荷与位移曲线如图5所示,从载荷位移曲线可以看出H形梁受压过程中,在临界值时达到最大承载力,进入后屈曲阶段后载荷没有增加。
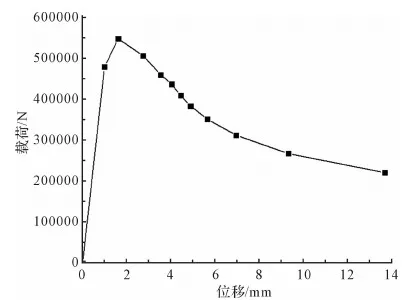
图5 H形梁压缩载荷位移曲线Fig.5 Compressive load-axial displacement curves of H-section beam
4 根据规范推荐公式计算
钢结构设计规范[11]推荐的实腹式轴心受压构件的稳定性按公式(3)计算。
(2)
式中,N为所计算构件段范围内的轴向压力,此处N待定;φ为弯矩作用平面内的轴心受压构件稳定系数,此处根据规范[11]查得φ=0.303;f为钢材的抗压强度设计值,此处根据规范[11]查得f=215MPa。
将已知数代入公式(2)并取等号得屈曲临界载荷为:
Nbuckling=508 131N
考虑到梁有10mm的初始偏心,以第一阶模态变形为梁的初始变形,根据钢结构设计规范[9]实腹式压弯构件,弯矩作用平面内的稳定性采用如下公式计算:
(3)
式中, N为所计算构件段范围内的轴向压力;此处N待定
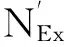

φx为弯矩作用平面内的轴心受压构件稳定系数,此处根据规范[7],查得φx=0.303;
Mx为所计算构件段范围内的最大弯矩,此处Mx为梁端部的初始偏心乘以轴向压力N。
则Mx=10×N
W1x为在弯矩作用平面内对较大受压纤维的毛截面模量,此处
βmx为等效弯矩系数,对于悬臂构件βmx=1.0;γx为与截面模量相应的截面塑性发展系数,此处查规范[11]得γx=1.2;f为钢材的抗压强度设计值,此处查规范[11]得f=215MPa。
将已知参数代入公式(3),同时取等式,可得
解之得按规范计算的承载力为:Ndefect=380 090N
4 讨论
H形梁轴心受压临界失稳载荷的有限元解与解析解的比较如表1所示,可以看出有限元计算结果与解析分析结果非常接近。表2列出了规范计算值与解析解和有限元解的比较。考虑工程实际情况复杂性和预测上的困难,规范计算值取值一般比较保守,通过安全系数来提高构件的可靠性,本文H形梁采用Q235钢塑性较好,由文献[9]可知杆件安全因数的参考数值对于塑性材料一般取ns=1.2~2.5。由表2可知,解析解、有限元解与规范计算值的比值分别为1.36、1.36、1.35均位于1.2~2.5之间。

表1 H形梁轴心受压临界载荷有限元解与解析解的比较

表2 H形梁规范计算值与解析解和有限元解的比较
对于屈曲后强度的解析解现有方法计算结果不够准确,现将有限元计算结果列于表3。后屈曲有限元计算已经考虑了构件的初始缺陷的影响,在这种情况下,本质上属于压弯构件的非线性大变形计算,由上文可知安全系数为ns=1.2~2.5。表4列出了有限元解与规范计算值的对比结果。从表4中可得有限元解与规范计算值得比值分别为1.47、1.44,均位于1.2~2.5范围内。

表3 H形梁轴心受压考虑初始缺陷的有限元结果比较

表4 H形梁后屈曲有限元解与规范计算值比较
通过分析可知,考虑初始缺陷的临界载荷明显低于未考虑缺陷的临界载荷值。由解析分析显示,该梁属于细长压杆,这种类型的构件在轴向压力达到临界值后,就丧失了承载力,所以临界值是承载力的上限,构件屈曲后承载力不可能再增加;通过有限元后屈曲强度分析该梁在达到临界载荷后,承载力逐渐降低,后屈曲强度没有进一步增长,属于极值点失稳,如图5所示,与解析分析结果相同。
5 结论
本文通过解析法、有限元分析方法,分别计算了屈曲临界载荷和考虑初始缺陷情况下的最大承载力,得出以下几点结论,供机械设计人员参考。
(1)解析解和有限元解均能准确的预测轴心受压梁的屈曲临界载荷,其精度十分接近。
(2)适用于欧拉公式的受压细长杆,屈曲后强度不会有所提高,属于极值点失稳,不能为结构提供安全储备。
(3)轴心受压梁的临界载荷规范计算值与有限元解和解析解比值位于文献[9]安全系数的合理范围1.2~2.5之间。
(4)采用后屈曲分析方法可以考虑材料的初始缺陷和材料的非线性,比较符合工程实际情况,它与临界值相比更接近规范计算结果。
(5)考虑初始缺陷和材料非线性的后屈曲承载力,有限元解与规范计算值的比值位于文献[9]安全系数的合理范围1.2~2.5之间。
(6)通过本文算例可以得出按规范计算的后屈曲承载力要比临界力更加保守。
[1] 署恒木. 工字形截面外伸梁的侧向屈曲[J]. 佳木斯大学学报,1999(4):392-396.
[2] 高旭,崔文好. 振动筛侧板强度分析及实验研究[J]. 重型机械,1999(4):24-27.
[3] 杜平虎,何学华. 地震对塔吊损坏的启示[J]. 中国特种设备安全,2009(3):65-67.
[4] 地震导致西安塔吊被震断[J]. 建筑安全, 2008(6):27-27.
[5] Hwon-mo Park, Jae-hyouk Choi. Evaluation on the post-buckling residual strength of H-shaped steel column[J]. Procedia Engineering, 2011,10:3387-3392.
[6] Daniel Y. Abebe, SijeongJeong, Jeonghyun Jang, Jaehyouk Choi, Jeong-Ung Park. Study on inelastic buckling and residual strength of H-section steel column member [J]. International journal of steel structures, 2015,15(2):365-374.
[7] 徐芝纶弹性力学[M].北京:高等教育出版社,2006.
[8] 冯贤贵. 细长压杆临界压力欧拉公式的统一推导[J]. 力学与实践,2003(4): 65-67.
[9] 苟文选·材料力学[M].北京:科学出版社,2010.
[10]邢静忠. ANSYS应用实例与分析[M]. 北京:科学出版社,2006.
[11]中华人民共和国建设部. GB50017-2003钢结构设计规范[S]. 北京:中国计划出版社,2003.
Research on stability of H-section cantilever beam unber axial load
WANG Wen-hao1,2,GOU Wen-xuan1,YANG Fan1,YAN Wu-zhu1
(1. School of Mechanics, Civil Engineering and Architecture, Northwestern Polytechnical University, Xi’an 710129,China;2.School of Mechanical Engineering,Taiyuan University of Science and Technology,Taiyuan 030024,China)
Compressed H-section beams or columns are widely used as structure members of mechanical equipment, and so it is very important that precisely forecast its bearing capacity. In this paper, the critical buckling load and the post-buckling bearing capacity considering initial imperfection was calculated by analytic method and finite element method (FEM). By analysis the main conclusion is as follows: firstly, the result of post-buckling considering initial imperfection is closer to reality condition than critical buckling load which is not considering initial imperfection; secondly, the post-buckling bearing capacity of slender compression member meeting conditions of Euler formula is not increased, and therefore the post-buckling bearing capacity cannot provide enough margin of strength; lastly, discrepancies between FEM results and code results are that the latter takes account the coefficients of safety.
cantilever beam; buckling; post-buckling
2016-05-10;
2016-06-15
山西省自然科学基金(2013011022-6)
王文浩(1976-),男,讲师,博士研究生,研究方向:先进材料与结构的力学行为,机械设计等。
TU391
A
1001-196X(2016)05-0036-06

