变质量完整系统Tzénoff方程Mei对称性的共形不变性与守恒量

郑世旺

(商丘师范学院 物理与电气信息学院，河南 商丘 476000)



变质量完整系统Tzénoff方程Mei对称性的共形不变性与守恒量

郑世旺

(商丘师范学院 物理与电气信息学院，河南 商丘 476000)

针对变质量的完整约束力学系统建立了相应的Tzénoff方程,给出了Tzénoff方程Mei 对称性共形不变性成立时所需的条件,进一步研究了Mei对称性共形不变性所能导出的守恒量，得到了直接用Tzénoff函数来表达的该守恒量的表达式和能够导出这种守恒量的判定方程,最后用实例来说明研究结果的应用.

变质量；完整约束系统，Tzénoff方程，共形不变性，守恒量

0 引 言

众所周知，动量守恒、动量矩守恒、能量守恒等物理量的守恒规律，不但具有明显的物理意义，而且在工业革命、航空航天技术、国防科技等领域有着广泛应用.其实，在不同的动力学系统中，也存在着具体的、形式不同的守恒量，在这些守恒量中，有的物理意义明显，有的物理意义不明显，还有的守恒量须进一步探究其潜在的物理意义及其应用．通过什么方法来寻找实际力学系统的守恒律呢？德国科学家Noether给出了一种方法[1].进入新的世纪以来,对称性和守恒量的研究成为了我国学者的一个热点,并取得了丰硕成果[2-10].上世纪末,俄罗斯学者Galiullin等人首次研究了Birkhoff 系统的共形不变性或共形对称性，提出了共形不变性和共形因子的概念[11].我国学者从2008年开始研究了Lagrange 系统的共形不变性及其守恒规律[12]，从此推动了共形不变性及其守恒量的研究，现已扩展到许多领域[13-17]．Tzénoff方程如同Lagrange方程、Appell方程、Birkhoff方程、Nielsen方程一样是动力学微分方程的一种，近10年来关于该动力学方程对称性与守恒量的研究取得了不少成就[18-24],但关于Tzénoff方程共形不变性的研究成果不多，目前才刚刚起步[25-26]．

由于空中飞行的导弹、火箭、卫星、喷气飞机等航天器一般都是属于质量变化的动力学系统，故变质量动力学系统的研究对航空、航天领域有重要的理论价值，但由于系统的质量在不断变化之中，使其动力学研究变得更复杂、更困难，常质量系统仅仅是其特殊情况．本文针对完整约束力学系统在质量变化的条件下，研究了Tzénoff方程Mei对称性的共形不变性及其守恒量，力求给出该系统Mei对称性共形不变性的判定方程及其所能导出守恒量的具体形式及产生这种守恒量的必备条件，最后给出了研究结果的一个应用．

1 变质量完整系统的Tzénoff方程

若系统的质点数量为N，时刻t时第i个质点的质量和位矢分别为mi和ri,，在时间变化微量dt后,质点质量的变化量为dmi．则质点的质量可由广义坐标、广义速度和时间来确定，即

(1)

系统的Tzénoff函数为[27]

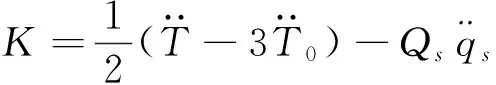
(2)

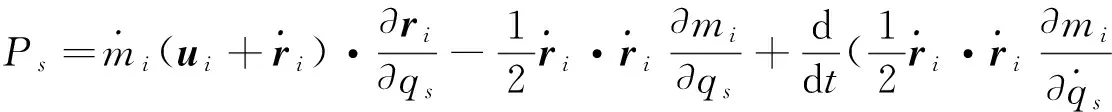
(3)

变质量完整约束力学系统的Tzénoff方程应为[24]

(4)

由方程(4)得

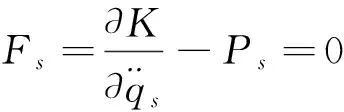
(5)

通过(5)式可直接求出广义加速度[21]

(6)

(6)式对时间求导可得到广义加加速度

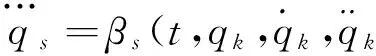
(7)

若构造Tzénoff函数为

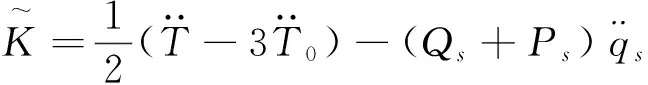
(8)

则变质量完整系统的Tzénoff方程将有更简单的形式

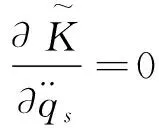
(9)

方程(4)和方程(9)虽然表面形式不同，其实是等价的．

2 变质量完整约束力学系统Tzénoff方程Mei对称性的共形不变性

设时间和广义坐标的无限小变换

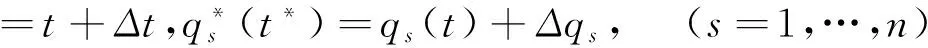
或

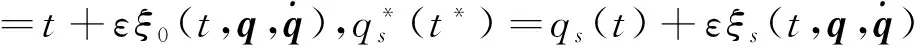
(10)

其中ε是一无限小参数，ξ0,ξs为无限小生成元.于是有

(11)

(12)

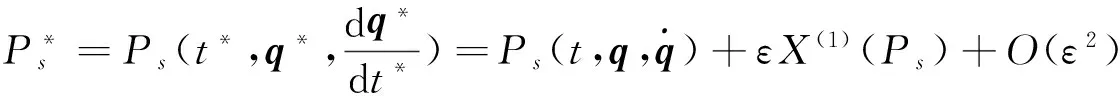
(13)

其中

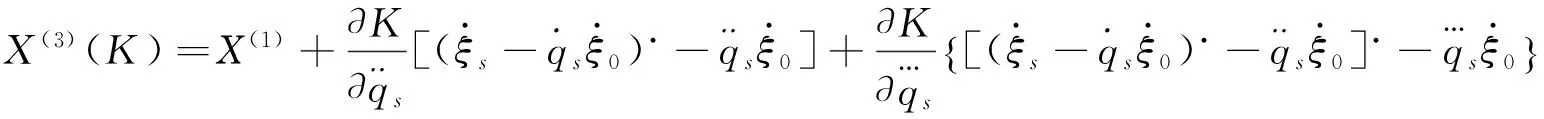
则称这种方程的形式不变性为变质量完整约束力学系统Tzénoff方程的Mei对称性．

若把(11)～(13)式代入方程(4)和(9)可得到

判据 若质量变化的完整约束力学系统Tzénoff函数K，在生成元ξ0,ξs变换下，满足方程

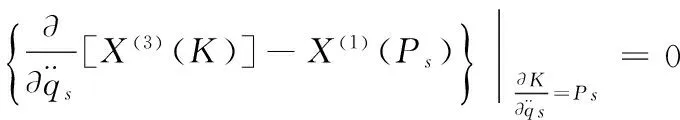
(14)

或

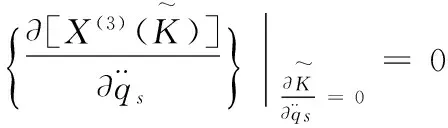
(15)

则Tzénoff方程具有Mei对称性.

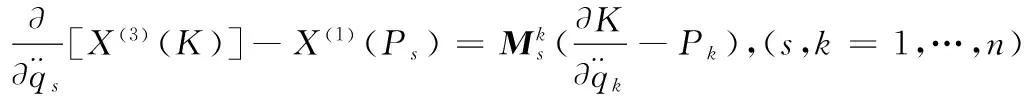
(16)

或

(17)

(18)

或

(19)

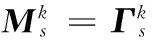
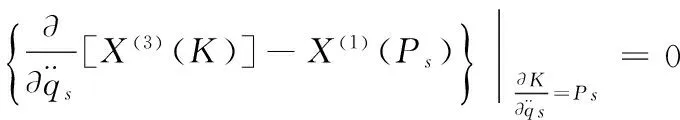
成为

(20)

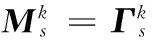
反之,若Tzénoff方程(4)成立共形不变性,方程(16)和(18)相减得到

(21)

3 变质量完整约束力学系统Tzénoff方程Mei对称性的共形不变性所产生的守恒量

完整约束力学系统在质量变化时，Tzénoff方程Mei对称性的共形不变性由于限制条件较多,寻找守恒量较为困难,但若满足下列条件，也可产生守恒量.

定理 完整约束力学系统在质量变化时，对于Tzénoff方程Mei对称性共形不变性的生成元ξ0,ξs，若存在函数G使

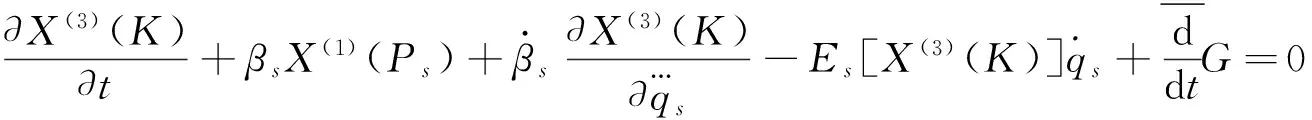
(22)

或

(23)

则系统直接产生一种新守恒量

(24)

或

(25)

(22)、(23)式中

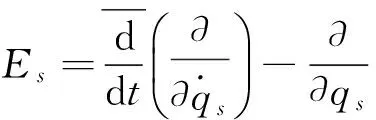
下面仅以第一种情况进行证明

证明 把(24)式对时间求导并考虑到方程(4)和Mei对称性共形不变性的判定方程(14)、(16)成立，有

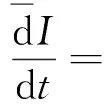
4 应用例子

已知变质量完整力学系统的Tzénoff函数为

(26)

其中

m(t)=m0e-γt, (m0和γ为常数)

(27)

微粒分离的相对速度为

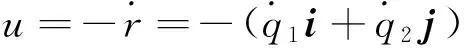
(28)

试研究该力学系统Mei对称性的共形不变性和其导出的守恒量.

解 由式(27)、(28)和(3)可知P1=0, P2=0，把Tzénoff函数(26)代入变质量完整系统的Tzénoff方程(4)，得

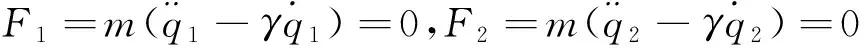
(29)

有

(30)

取ξ0=0,ξ1=q1,ξ2=q2,则有

(31)

有

(32)

所以,共形不变性的判定方程(16)成立,变质量完整约束力学系统具有Mei对称性的共形不变性,其共形因子

(33)

由(29)、 (32)式的关系,有

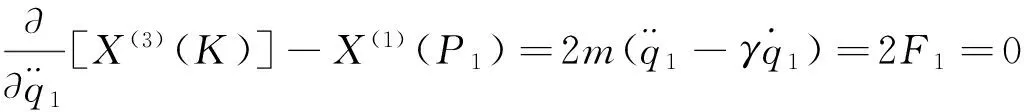
(34)

(35)

故Mei对称性判据方程(14)成立,系统同时也具有Mei对称性.

根据结构方程(22)得到.

(36)

由(36)、(24)式得新守恒量

5 结 论

针对完整约束力学系统在质量变化的状态下，给出了两种等价的Tzénoff方程，探究了该状态Mei对称性的共形不变性及其产生的守恒量，并给出了Mei对称性共形不变性的两种等价的判定方程及其所能产生的守恒量．该研究结果对探究变质量系统在共形不变性条件下的守恒规律有一定的参考价值．

[1]Noether A E.Invariance Variations problem s [J].Kgl Ges Wiss Nachr Göttingen Math Phys,1918,KI,II:235-257

[2]Mei Fengxiang.Form invariance of Lagrange system[J].Journal of Beijing Institute of Technology,2000,9(2):120-124.

[3]梅凤翔.约束力学系统的对称性与守恒量[M].北京：北京理工大学出版社,2004.

[4]Fu Jingli,Wang Xianjun,Xie Fengping.Conserved Quantities and Conformal Mechanico-Electrical Systems[J].Chinese Physics Letters,2008,25(7):2413-2416.

[5]Zhao Li,Fu Jingli.A new type of conserved quantity of Mei symmetry for the motion of mechanico electrical coupling dynamical systems[J].Chinese Physics B,2011,20(4):040201(1-4).

[6]刘畅，赵永红，陈向炜.动力学系统Noether对称性的几何表示[J].物理学报,2010,59(1):11-14

[7]方建会.Lagrange系统Mei对称性直接导致的一种守恒量[J].物理学报,2009,58(6):3617-3619

[8]Li Yanmin.Lie Symmetries,Perturbation to Symmetries and Adiabatic Invariants of a Generalized Birkhoff System[J].Chinese Physics Letters,2010,27(1): 010202(1-4)

[9]Shao Kai Luo,Zhuang Jun Li,Wang Peng,Lin Li.A Lie symmetrical basic integral variable relation and a new conservation law for generalized Hamiltonian systems[J].Acta Mechanica,2013,224(1): 71-84

[10]李凯辉,刘汉泽,辛祥鹏.一类高阶非线性波方程的李群分析、最优系统、精确解和守恒律[J].物理学报，2016,65(14):140201(1-7).

[11]Галиуллин А С，Гафаров Г Г，Малайшка Р П，et al.Аналитическая Динамика Систем Гельмгольца，Виркгофа，Намбу：Монография[M].Москва：Редакция Журнала “Успехи Физических Наук”，1997.

[12]蔡建乐,梅凤翔.Lagrange 系统Lie点变换下的共形不变性与守恒量[J].物理学报,2008,57(9):5369-5373.

[13]刘畅,刘世兴,梅凤翔,等.广义Hamilton 系统的共形不变性与Hojman守恒量[J].物理学报,2008,57(11):6709-6713.

[14]王廷志,韩月林.相对运动非完整动力学系统的共形不变性与守恒量[J].江南大学学报( 自然科学版),2013,12(2):234-238.

[15]王小明,李元成,夏丽莉.机电系统Mei对称性的共形不变性与守恒量[J].贵州大学学报(自然科学版),2009,26(6):32-38.

[16]陈向炜,赵永红,刘畅.变质量完整动力学系统的共形不变性与守恒量[J].物理学报,2009,58(8): 5150-5154.

[17]李彦敏.变质量非完整力学系统的共形不变性[J].云南大学学报( 自然科学版),2010,32(1):52-57.

[18]Zheng Shiwang,Jia Liqun,Yu Hongsheng.Mei Symmetry of Tzénoff Equations of Holonomic System[J].Chinese Physics,2006,15(7):1399-1402.

[19]Zheng Shiwang，Xie Jiafang,Li Yanmin.Mei symmetry and conserved quantity of Tzénoff equations for nonholonomic systems of non-Chetaev,s type[J].Communications in Theoretical Physics,2008,49 (4) :851-854.

[20]郑世旺,解加芳,陈向炜，等.完整系统Tzénoff方程的Mei对称性直接导致的另一种守恒量[J].物理学报,2010,59(8):5209-5212.

[21]Zheng Shiwang,Wang Jianbo,Chen Xiangwei,Xie Jiafang.Mei symmetry and new conserved quantities of Tzénoff equations for the variable mass higher-order nonholonomic system[J].Chinese Physics Letters,2012,29(2):020201(1-4).

[22 郑世旺,陈梅.非完整系统Tzénoff方程的Mei对称性所对应的一种新守恒量[J].云南大学学报,2011,33(4):412-416.

[23]郑世旺,王建波,陈向炜,等.变质量非完整系统Tzénoff方程的Lie对称性与其导出的守恒量[J].物理学报,2012,61(11):111101(1-5).

[24]郑世旺,王建波,解加芳.变质量完整系统Tzénoff方程的Lie对称性与其导出的守恒量[J].商丘师范学院学报,2011,27(12):17-21.

[25]郑世旺，赵永红.完整系统Tzénoff方程Lie对称性的共形不变性与守恒量[J].商丘师范学院学报,2015,31(6):39-43.

[26]郑世旺.完整系统Tzénoff方程Mei对称性的共形不变性与守恒量[J].商丘师范学院学报,2016,32(3):24-28.

[27]梅凤翔,刘端,罗勇.高等分析力学[M].北京：北京理工大学出版社,1991.

[责任编辑：徐明忠]

Conformal invariance and conserved quantity of Mei symmetry for Tzénoff equations in holonomic systems with variable mass

ZHENG Shiwang

(School of Physics and Electrical Information,Shangqiu Normal University,Shangqiu 476000,China)

The corresponding Tzénoff equation is established for the holonomic systems with variable mass.Then the conditions which needed to form the conformal invariance and conserved quantity of Mei Symmetry for Tzénoff equations are given.The conserved quantity derived from conformal invariance of Mei symmetry is further explored.By using the Tzénoff functions,the discriminating functions of conserved quantities and the criterion equations which deduce the conserved quantities are directly obtained.Finally,an example is given to illustrate the application of the research results.

variable mass;holonomic constraint systems;Tzénoff equations;conformal invariance;conserved quantity

2016-09-22

国家自然科学基金资助项目(11372169)

郑世旺(1963—)，男，河南兰考县人，商丘师范学院教授，主要从事分析力学的研究.

O316

A

1672-3600(2016)12-0032-05