圆盘颗粒DDA接触算法及冲量法
陈 孚,喻 勇
(西南交通大学 a.力学与工程学院; b.应用力学与结构安全四川省重点实验室,成都 610031)
圆盘颗粒DDA接触算法及冲量法
陈 孚a,喻 勇b
(西南交通大学 a.力学与工程学院; b.应用力学与结构安全四川省重点实验室,成都 610031)
介绍了圆盘颗粒不连续变形分析(DDA)理论。推导了圆盘与边界、圆盘与圆盘的罚函数法接触子矩阵。在罚函数法和曾广拉格朗日法下编写程序模拟了单个圆盘与边界碰撞、折斜面上的运动和多圆盘在封闭边界内的运动等3个算例。研究了罚函数法和增广拉格朗日法处理接触时刚度变化对系统机械能的影响,发现碰撞速度较大时,系统机械能的变化在不同刚度取值组合下相差很大。为解决模拟碰撞时存在的机械能变化不准确的问题,在计算中引入冲量法,用于计算圆盘与圆盘、圆盘与边界以及圆盘与凸角碰撞后的分离速度,以更新DDA算法中的初始速度。将冲量法编入程序在不同恢复系数和摩擦角条件下重新模拟算例,发现改善后的算例程序可较好地模拟多圆盘在运动过程中的机械能变化。
圆盘颗粒DDA;接触刚度;机械能;冲量法
非连续变形分析方法(discontinuous deformation analysis,DDA)[1]是石根华教授基于岩体这类非连续介质提出的一种分析块体系统运动和变形的数值分析方法。
DDA理论一经提出就以其严谨的运动学方案吸引了众多的学者和岩土技术工程师的注意,并被广泛应用在岩土工程中。在过去的几十年中,DDA在理论和应用上都有了长足的发展。Jing[3]将DDA理论应用在岩土工程中。Thomas PA[4]定性地证明了DDA理论模拟块体系统运动的有效性。MacLaughlin[5]验证了过百的DDA算例。Hatzor[6]将DDA理论应用在岩质边坡和地下硐室的稳定性研究上并证明DDA理论的有效性。大西有三[7]对三维DDA理论进行了研究。姜清辉[8]提出了DDA理论的Newmark积分方案。夏才初[9]使用DDA理论分析岩石破坏过程中潜在的破坏路径。张秀丽[10]用改进的非连续变形分析方法对某公路隧道进行稳定性分析,采用行波法在计算区域内自动生成三角形块体,同时考虑了预应力锚杆对隧道围岩的加固作用;将计算得到的结果与现场监测结果进行对比,两者基本吻合。马永政[11]采用具有插值特性自然单元法中的自然邻接点插值NNI法,具有很好的计算精度和无网格特征。为分析大块体弯曲、裂纹扩展破坏形式等提供了分析基础。甯尤军[12]采用DDA方法模拟了节理岩体中的水平柱状炮孔抛掷爆破问题,输出了爆腔的体积扩张和压力衰减时间曲线,很好地模拟了岩石爆破过程中的炮孔扩张、岩体破坏、块体抛掷和爆堆形成过程。朱爱军[13]针对填石路堤工程,编制了大型数值计算程序,采用块体随机生成、块体粒径控制及块体自然堆积的方法建立散体系统的DDA模型,对路堤的分层铺设、碾压及工后沉降变形等进行模拟分析。
圆盘颗粒介质DDA理论的研究处于初期阶段,Ke对刚性边界中二维圆盘组成的颗粒介质做了完整表述。Beyabanaki对比了处理接触关系的罚函数法和增广拉格朗日法,表明增广拉格朗日法可更有效地控制块体间的相互侵入。罚函数法处理圆盘间接触关系时,接触力会随着接触刚度的变化而变化,所以,圆盘的速度解和机械能会产生误差,特别是在接触点的相对速度较大时上述误差较大。本文推导了基于罚函数法的圆盘与边界间、圆盘间接触子矩阵和新的位移修正公式,确定圆盘颗粒DDA理论处理圆盘碰撞运动的条件,并且引入冲量法对圆盘间激烈碰撞问题进行了处理。
1 刚性圆盘DDA理论
1.1 刚性圆盘位移
文献[2]中,圆盘简化为刚体,在运动过程中无变形。圆盘有2个刚体位移和1个转角位移,即u0,v0,γ0。
[u,v]T=[Ti(x,y)]·[Di]
(1)
(2)
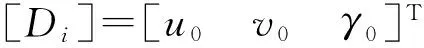
DDA是一种隐式方法,涉及一平衡方程组,如式(1)所示,以块体数为N的系统为例。方程组的未知数是块体的位移与转角[1]。
(3)
块体系统势能表达为Π;参考文献[1]第二章内容,方程组中系数矩阵与常数矩阵由式(4)求出。
(4)
由于位模式是1阶的,块体在发生刚体转动时,块体上点位移误差较大,本文中用下式修正下文中参考点的位移。
(5)
1.2 接触模型
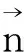
(6)
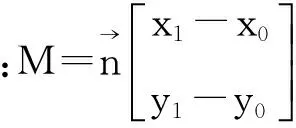
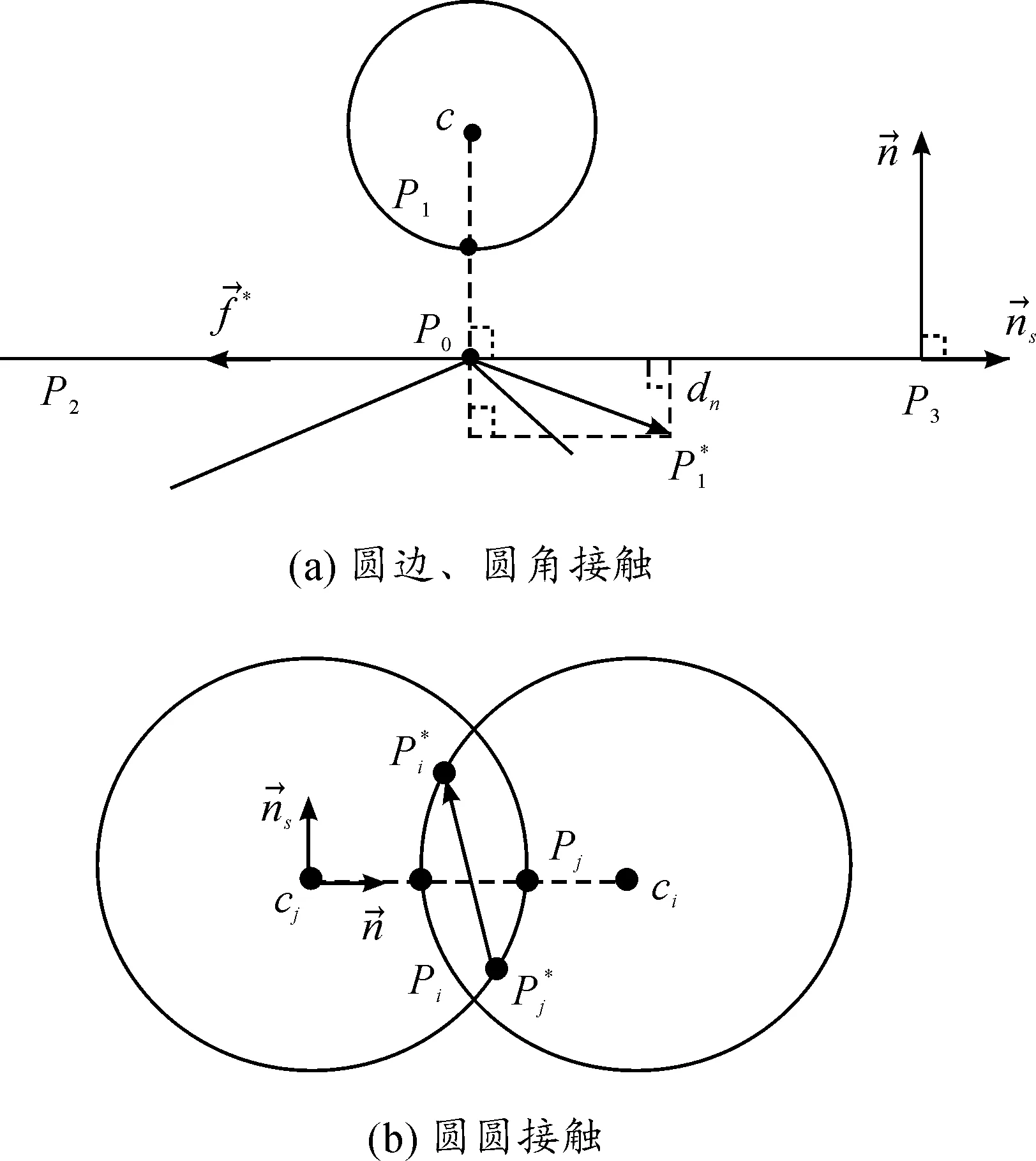
图1 接触模型
法向弹簧势能为
(7)
Kn是法向弹簧刚度,由式(4)得法向子矩阵为:
Kn[Hi]T[Hi]→[Kii]
(8)
-KnM[Hi]T→{Fi}
(9)
同理,切向子矩阵为:
Ks[HS]T[Hs]→[Kii]
(10)
-KSS0[Hs]T→{Fi}
(11)
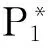
|Kndntan(φ)|
(12)
式(12)中φ为摩擦角,摩擦力势能为:
(13)
(14)
变量s的作用是保证πf值为正值。
摩擦力子矩阵为:
(15)
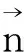
法向、切向、摩擦力子矩阵和圆盘与直边接触时的子矩阵形式相同。
法向侵入量为
G+[Hi]{Di}-[Qj]{Dj}
(16)
同理,法向子矩阵为:
(17)
由摩擦力子矩阵可得摩擦力做功为
(18)
同理得:
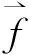
(19)
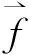
(20)
(21)
根据增广拉格朗日法,在第h步迭代时,法向弹簧势能如下:
(22)
κh=κh-1+Kndn
(23)
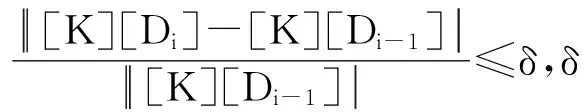
2 算例模拟及分析
将上一节中的颗粒DDA理论编成程序,模拟了5个算例。本文算例中圆盘相关参数为:弹性模量E=1 000 GPa,泊松比υ=0.2,面积密度M=2 300 kg/m2,重力加速度g=9.8 m/s2。
算例1中,增广拉格朗日法处理半径10 m的圆盘以10 m/s的速度与边界碰撞,如图2(a)所示。
算例2中,如图2(b),单个圆盘在斜面上运动;斜边与水平边夹角θ=45°,摩擦角φ=15°,圆盘无初始线速度和角速度。
算例3中,如图2(c),多圆盘在多边封闭边界里运动,无初始速度,初始状态如图2所示。
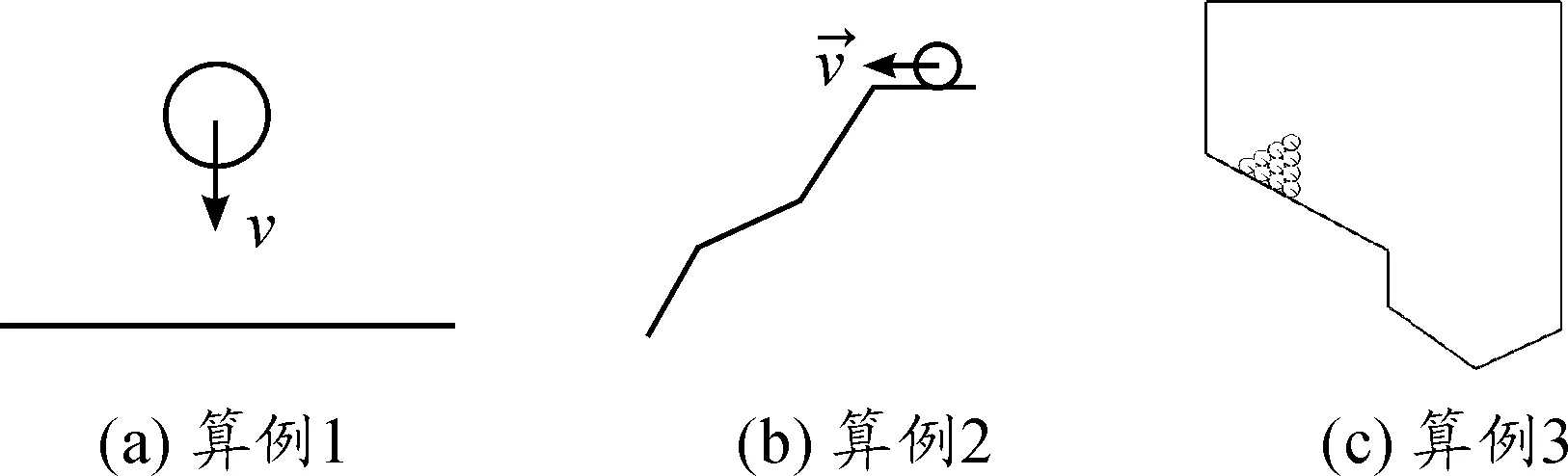
图2 初始状态
算例1中,使用增广拉格朗日法处理圆盘与边界的碰撞。如图3(a)所示,不同接触刚度下圆盘与边界碰撞时机械能变化相差很大,同时出现了突增的现象。
算例2中,使用罚函数法处理圆盘与边界的碰撞。算例中有摩擦力作用,如图3(b)所示,摩擦角为φ=15°时,圆盘机械能在不同刚度组合作用下,圆盘与边界连续接触时圆盘机械能变化相差不大,当圆盘与边界发生碰撞时圆盘机械能在不同刚度组合下相差很大。
算例3中,使用罚函数法处理圆盘与边界的碰撞、圆盘与圆盘碰撞。如图2(c)所示,摩擦角为φ=15°时,圆盘总机械能在不同刚度组合下随时间的变化,当圆盘系统未崩塌之前在不同刚度组合下,圆盘系统机械能和变化相差不大,当系统崩塌后机械能和发生了突增;刚度组合为Kn=0.301E,Ks=0.004E时与理论解的相对误差最大,为820.22%。可见本文中的罚函数法和增广拉格朗日法在处理圆盘碰撞时机械能的准确性对接触刚度有较强的依赖性,这主要是因为两种方法求解的接触力不准确。
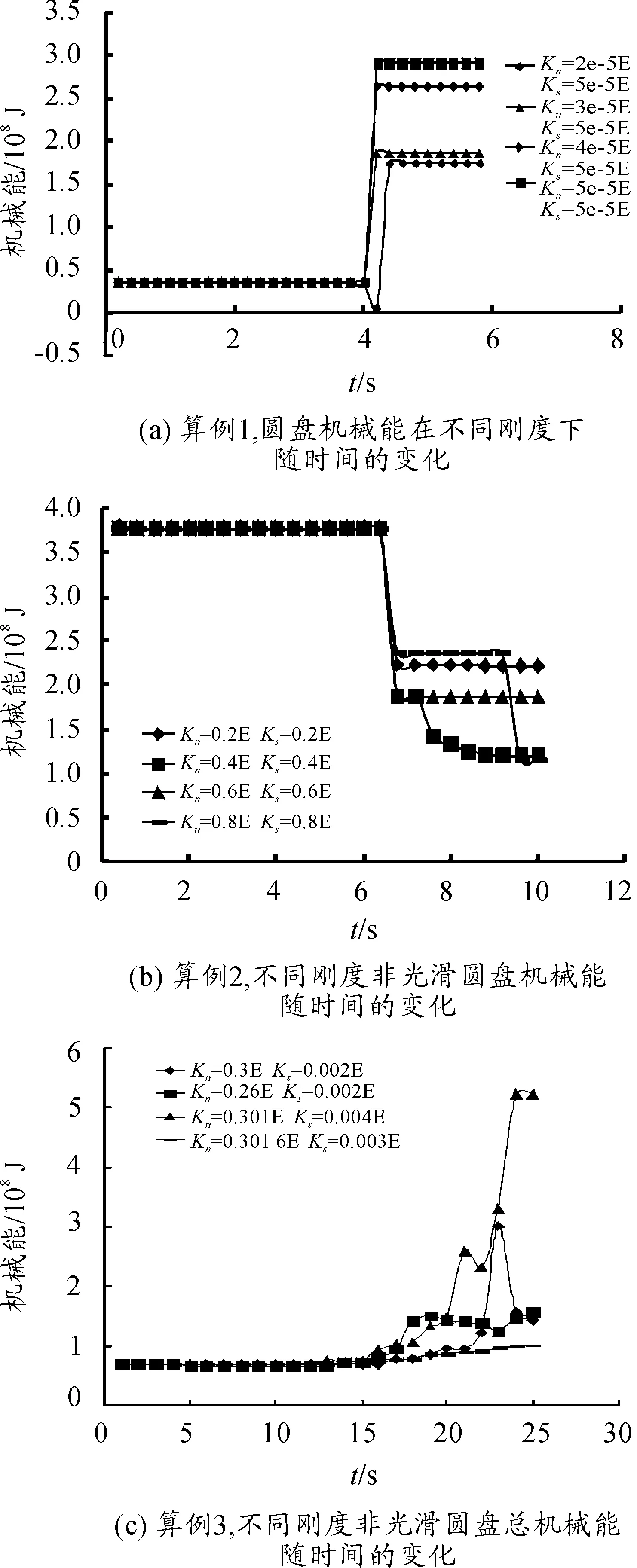
图3 机械能变化
3 冲量法
罚函数法和增广拉格朗日法处理圆盘碰撞时,系统机械能误差对接触刚度,因此引入冲量法缓解这个问题。使用冲量法计算碰撞后的块体速度,以此速度作为下一时间步中块体的初速度代入DDA程序,继续进行计算。
(24)
(25)
(26)
(27)
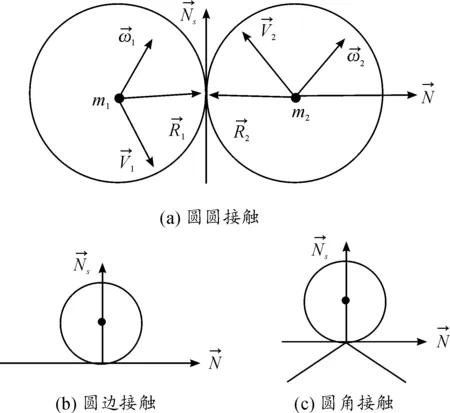
图4 碰撞示意图
(28)
同时假设圆盘碰撞时在接触点处,没有滑动。满足下列关系:
(29)
(30)
(31)
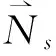
(32)
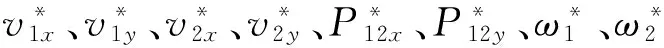
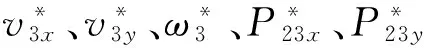
将冲量法理论程序编入本文DDA算例2、3程序中。算例2、3中进行了4种方案的计算,每种方案中的恢复系数与摩擦角不相同,如表1。
图5(a)为算例2在不同参数组合下圆盘机械能随时间的变化,恢复系数为1和无摩擦角时圆盘机械能没有损失;恢复系数为1和摩擦角为15°圆盘与边界碰撞时,机械能的减少是由摩擦力作用造成的,较为符合实际情况;当恢复系数为0.9,圆盘与边界碰撞时,圆盘机械能突减。图5(b)为算例3中圆盘系统机械能和在不同参数组合下随时间的变化。恢复系数和摩擦角分别为1和15°时,机械减少是由摩擦力损耗造成的;当恢复系数为0.9时总机械能减少得较快,最终会稳定下来;当恢复系数和摩擦角分别为1和0°时总机械能没有变化,圆盘一直处于运动状态;图5(c)、(d)、(f)分别为圆盘系在不同参数条件下的最终稳定状态,3种状态都不相同。图5(d)是恢复系数和摩擦角分别为1和0°条件下,当t=80 s时圆盘系统的运动状态,可见在上述条件下圆盘系统在运动过程中无能量损失,永远停不下来。
综上所述,冲量法可较好地改善机械能突增的现象。

表1 算例2、3中的参数取值
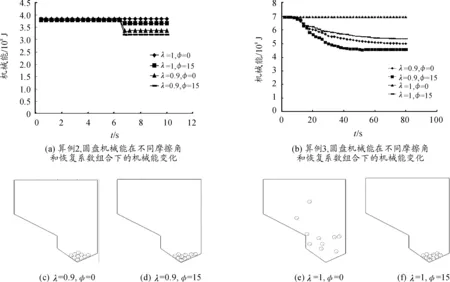
图5 机械能变化及稳定状态
4 结论
本文推导了圆盘颗粒DDA罚函数法接触子矩阵,编写了罚函数法和曾广拉格朗日算例程序,发现系统机械能在不同接触刚度值下相差很大,这主要是接触力计算不准确。引入冲量法计算得到圆盘碰撞分离速度,用其更新圆盘在碰撞后时间步的初始速度。将冲量法和圆盘颗粒DDA理论结合起来模拟了多圆盘在复杂边界上运动,根据圆盘系统总机械能在不同恢复系数和摩擦角组合的条件下随时间的变化情况,可见引入冲量法后,算例程序可以较好地模拟多圆盘运动过程中的机械能变化。
[1] 何传永,孙平.非连续变形分析方法程序与工程应用[M].北京:中国水利水电出版社,2009.
[2] KE TE-CHIH,JONATHAN B Bray.Modeling of particulate medal using discontinuous deformation analysis [J].Journal of Engineering Mechanics,1995,121:1234-1243.
[3] JING L,HUDSON J A.Numerical methods in rock mechanics [J].International Journal of Rock Mechanics and Mining Sciences,2002(4):409-427.
[4] THOMAS P A.Discontinuous deformation analysis of particulate media[D].California:University of California,1997.
[5] MACLAUGHLIN M M,DOOLIN D M.Review of Validation of the Discontinuous Deformation Analysis (DDA) method[J].International Journal for Numerical and Analytical Methads in Geomechanics,2006,30(4):271-305.
[6] HATZOR YH,BAKUN M D.Modeling dynamic deformation in natural rock slopes and underground openings with DDA [J].Geomechanics and Geoengineering,2011,6(4):283-92.
[7] 吴建宏,大西有三,石根华,等.三维非连续变形分析(3D DDA)理论及其在岩石边坡失稳数值仿真中的应用[J].岩石力学与工程学报,2003,22(6):937-942.
[8] 姜清辉,周创兵,漆祖芳.基于Newmark 积分方案的DDA 方法[J].岩石力学与工程学报,2009,28(s):2778-2783.
[9] 夏才初,许崇帮.非连续变形分析(DDA)中断续节理扩展的模拟方法研究和试验验证[J].岩石力学与工程学报,2010,29(10):2027-2033.
[10]张秀丽,焦玉勇,刘泉声,等.用改进的DDA方法模拟公路隧道的稳定性[J].岩土力学,2007(8):1710-1714.
[11]马永政,郑宏,李春光.应用自然邻接点插值法的块体非连续变形分析[J].岩土力学,2008(1):119-124.
[12]甯尤军,杨军,陈鹏万.节理岩体爆破的DDA方法模拟[J].岩土力学,2010(7):2259-2263.
[13]朱爱军,曾祥勇,邓安福.数值流形方法框架下散体系与连续介质共同作用模拟[J].岩土力学,2009(8):2495-2500.
[14]卞大鹏,吴其俊.高速抱轨制动过程中摩擦片温度场研究[J].四川兵工学报,2015,36(6):70-73.
[15]王祥洲,何天稀,陈波水,等.纳米介孔碳的制备及其摩擦学性能研究[J].重庆理工大学学报(自然科学),2016,30(2):47-52.
[16]罗京帅,邢志国,王海斗,等.服役条件对表面织构摩擦学性能影响的研究进展[J].功能材料,2016,47(1):1028-1033.
[17]何仁,汤宝,赵强.电磁与摩擦制动集成系统切换控制策略[J].江苏大学学报(自然科学版),2015(2):125-129.
(责任编辑 杨文青)
Contact Algorithm of Disk-Based Particle DDA and Impulse-Based Method
CHEN Fua, YU Yongb
(a.School of Mechanics and Engineering; b.Applied Mechanics and Structure Safety Key Laboratory of Sichuan Province, Southwest Jiaotong University, Chengdu 610031, China)
The theory of disk-based DDA (Discontinuous Deformation Analysis) is presented. Based on penalty method,the sub-matrices for disk to boundary and disk to disk are derivated. They are as follows: a single disk running into boundaries, a single disk on on multiple slopes and disks within a closed boundary. The influence of penalty value on mechanical energy was studied when penalty method and augmented Lagrangian method are used to deal with the contact. The change of mechanical energy within the system show strong dependence on the stiffness of the system in collisions. To solve the problem above, the impulse-based method is used to calculate the velocity after every collision. This method is coded into the program of previous examples and simulates movements under different combinations of recovery efficient and friction angle. It is shown that the method can well simulate the mechanical energy of disks within a closed boundary.
disk-based particle DDA; contact stiffness; mechanical energy; impulse-based method
O324
A
1674-8425(2016)11-0071-07

