New Insights on Energy Conserved Planar Motion

Maruthi R.Akellaand Sofokli Cakalli

New Insights on Energy Conserved Planar Motion

Maruthi R.Akella1and Sofokli Cakalli2

The planar motion of a particle within an arbitrary potential field is considered.The particle is additionally subject to an external force wherein the applied thrust-acceleration is constrained to remain normal to the velocity vector.The system is thus non-conservative but since the thrust force is non-working,the total energy is a conserved quantity.Under this setting,a major result of fundamental importance is established in this paper:that the flight direction angle(more precisely,the sine of the angle between the position and velocity vectors)is shown to always satisfy a linear first-order differential equation with variable coefficients that depend upon the underlying potential function.As a consequence,an analytical solution for the flight direction angle can be obtained directly in terms of the particle’s distance from the center of the field for a significant number of special cases for the potential function.In the case of J2perturbed spacecraft motion within equatorial orbits,the problem is reduced to that of solving an incomplete elliptic integral.Another important implication of the main result established here is that motion problems subject to velocity-normal thrusting can always be reduced to the study of equivalent single degree-of-freedom conservative systems with an effective potential function.The paper concludes with various examples of both academic and practical interest including the study of bounded two-body Keplerian orbits and hodograph interpretetions

Energy conserved spacecraft motion,flight direction angle,velocitynormal thrusting,effective potential,hodograph interpretation.

1 Introduction

The problem of continuous thrusting in the two-body problem has rich history and has been extensively studied for spacecraft applications.However,analytical solutions to these problems are available only for very few special cases.For example,some of the earliest work was done by Tsien(1953)using circumferential thrust for escaping from an initial circular orbit.The classical problem of spacecraft motion subject to a constant radial thrust is remarkable in the sense that it is fully integrable;accordingly,it has been extensively investigated[Prussing(1998);Akella(2000);Akella and Broucke(2002)].The problem of tangential thrust acceleration also allows for some analytical solutions as established by Benney(1958),as well as an exponential sinusoid solution approximations for many revolution transfers and interplanetary trajectories. The problem of continuous thrusting in the direction perpendicular to the velocity vector has however received very limited attention,albeit the fact that energy remains a conserved quantity for these classes of problems.Notable exceptions are recent work by Hernandez and Akella(2015)wherein initial circular orbits are considered with a focus on mission design and orbit transfer analysis.An immediate consequence of thrusting normal to the velocity vector is that,no matter how high the acceleration magnitude,trajectories always remain bounded so long as thrusting commences from initially bounded orbits.Energy conservation in this class of problems is reminiscent of the constant-radial-thrust acceleration problem wherein angular momentum is the conserved quantity rather than the energy.In the radial problem,there is one additional integral of motion;therefore,the problem can be solved analytically[Akella and Broucke(2002)].On the other hand,a full analytical solution is not possible for the case thrusting normal to the velocity,which has only one known constant.

The main contribution of this paper is that the flight direction angle,i.e.,the angle between the position and velocity vectors satisfies a linear first-order ordinary differential equation in terms of the radial distance.This remarkable result holds for arbitrary potential fields.As a consequence,an effective potential can be interpreted to reduce the original system from two to a single degree of freedom system.Our problem can therefore be shown to be equivalent to the one-dimensional motion of a unit point mass in the central force field subject to the velocity-normal thrust acceleration.The reminder of the paper is organized as follows.In Sec.II,the equations of motion are derived in both inertial and body-fixed rotating coordinates.The first order linear differential equation govering the flight direction angle is also established in this section.Several special case examples for potential functions are shown in Sec.III together with a discussion on the effective potential formulation.Wefinalize the paper with some concluding remarks in Sec.IV.

2 Coordinate Frames and Problem Statement

Consider the planar motion of a point-mass object described by position vectorvelocity vectorand potential energyW(r)wherer=the radial distance from the origin of an inertial frame.The inertial frame is taken to have a basisAdditionally,we consider a body-fixed frameis the unit vector in the velocity direction andis the unit vector that is normal to the instantaneous velocity direction.For this study,it needs to be noted that a constant external acceleration vector u is assumed to be acting along the-direction.

2.1 Equation of Motion

The general equations of planar motion subject to external perturbation acceleration u in Cartesian coordinates are

where as stated already,u is the thrust-acceleration applied normal to the velocity direction;i.e.,uTv=0.The thrust acceleration is assumed to be parameterized through

On the other hand,since the thrust is applied perpendicular to the velocity vector,the total energy defined by

is a conserved quantity,wherev= ‖v‖.This can be readibly confirmed by taking the derivative ofEwith respect time along trajectories defined by Eq.1,such that,

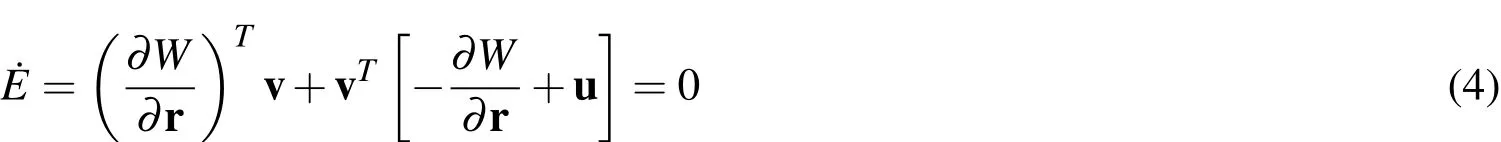
An immediate consequence of rearranging Eq.3 is that velocity magnitude is dependent only on radial distance,i.e.,

Letsbe the arc length of the path measured relative to the origin of the inertial frame.Suppose the velocity vector v makes an angleθwith the inertialdirection.Letρdenote the radius of curvature of the path,i.e.,ρ=ds/dθ.Then,kinematics leads to the velocity vector given by

and the acceleration vector

From the governing equations of motion in Eq.1,the total acceleration experienced by the body resolved in the moving frameis given by

调查表明：不同品种金丝小枣的浆烂果病发病率显著不同，无核金丝、曙光5、曙光6抗浆烂果病能力很强，在发病盛期（9月中旬），上述3个品种浆烂果病平均发病率分别为3.73%、3.67%和2.9%，明显低于普通品种。2017年9月中旬，普通金丝小枣浆烂果率达到13.5%时，无核金丝、曙光5、曙光6的浆烂果率仅为2.3%、2.9%、2.2%。同时，我们观察到金丝小枣8月中旬以前基本不感染浆烂果病，8月中旬后随降雨量增大，烂果骤增，所以在金丝小枣果实浆烂前采鲜果出售是减少损失的有效举措。

It should be noted thatγ∈[0,π)by definition.Combining Eq.1,Eq.6,and Eq.9,it can be established that

Next,comparing terms from Eq.7 and Eq.8,it follows that

Straightforward calculus provides the useful identity

Defining the functionβas

and substituting the following Bernoulli formula for the inverse of the radius curvatureρ[Battin(1999)],

After performing some straightforward algebra,we obtain the following first-order linear ordinary differential equation governingβas given by

whereinv2=2[E−W(r)]needs to be interpreted from Eq.5.The establishment of this“Fundamental Equation”governing the flight direction angle(specifically,sinγ)is the major result of this paper.Given the fact that Eq.17 is a linear differential equation in terms of radial distancer,the important implication is that sinγcan always be directly expressed as a function of radial distancerfor any potential functionW(r).

3 The Flight Direction Angle and Interpretation of the Effective Potential Function

As was shown in the foregoing section,an analytical solution for the flight direction angle can be obtained in terms of the particle’s distance from the center of the field.There is yet another important consequence to this result.Recall that the energy constant of motion in Eq.3 can also be expressed as

Using Eq.5 in Eq.18 results in

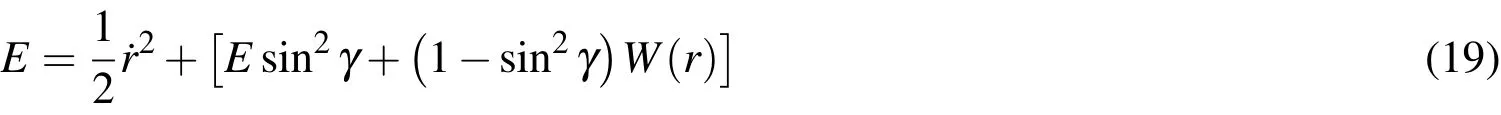
which allows for the interpretation of an effective potential function

such that the energy constantE=˙r2/2+Weff(r)corresponds to the motion of an equivalent single-degree-of-freedom conservative system.The reminder of this section will consider various special cases for the potential functionW(r)to further illustrate the current discussion.

3.1 Linear Harmonic Oscillator

The potential function for linear harmonic motion in the plane is defined byW(r)=(ω2r2)/2 whereω＞0 is the constant associated with the unforced oscillation frequency.Substituting this particular expression forW(r)forv2in Eq.5 and subsequently in Eq.17 results in

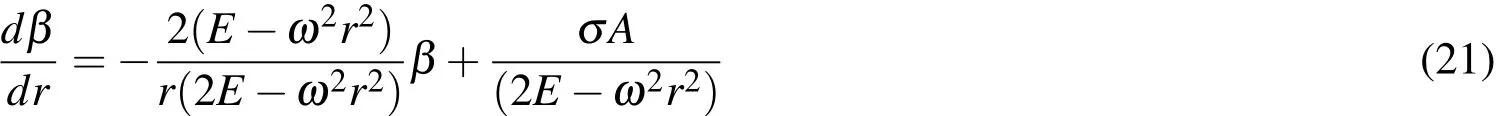
Allowing for initial conditionsr(0)=r0andβ(r0)=β0for the flight-direction angle,a closed-form solution of Eq.21 can be written as

which can be easily verified by substitution in Eq.21.It can be seen that Eq.22 represents the analytical solution forw(r)≡sinγ(r).

3.2 Kepler 2-Body Motion

For the case of two-body motion,the potential energy is given by the expressionW(r)=−µ/rwithµbeing the gravitational constant.Using this expression in Eq.5 presents

which can be substituted within Eq.17 to provide the following analytical solution for the flight direction angle,specifically forβ(=sinγ);i.e.,

wherein the initial conditionsr(0)=r0andβ(r0)=β0had been applied.It should be stated that a special case of this particular result was discussed earlier by Hernandez and Akella(2015)and Hernandez(2014),wherein an initial circular orbit was assumed(more specifically,µ=1,r0=1,β0=1).However,the result established here in Eq.24 generalizes the analytical solution for the flight direction angle for arbitrary bounded initial Keplerian orbits.Given the fact that the flight-direction angle is an explicit function of radial distancerfrom Eq.24,an extremely elegant interpretation for intial non-circular orbits can be made within the hodograph plane through Figure 1.Specifically,it needs to be noted that for true Keplerian motion,i.e.,withA=0,the hodograph representation for the velocity vector in Fig.1 follows the classical result of being a circle having radius equaling the eccentricity e of the initial orbit with the center of the circle at(1,0).On the other hand,when thrusting is introduced(A/=0),the hodograph circle is seen to deform into an“oval”shape with inward thrusting(σ=+1),and a“teardrop”with outward thrusting(σ=−1).

Figure 1:The hodograph interpretation for initial non-circular orbits(eccentricity,e＞0).

3.3 J2Perturbed Equatorial Orbits

The final special case analyzed here corresponds to J2perturbed motion for equatorial earth orbits.In the absence of thrusting,an analytical solution for this problem was obtained by Jezewski(1983)in terms of elliptic integrals.We now consider motion subject to constant acceleration continuous thrusting along a direction normal to the velocity vector.The potential function is given by

wherein the constantJ0is given by

withJ2being the perturbation coefficient due to Earth’s oblateness andreis the equatorial radius of the Earth.The solution for the flight direction angle from Eq.17 in this case reduces to

4 Conclusions

This paper establishes a fundamental result for the flight direction angle in terms of radial distance in the case of planar motion subject to constant acceleration continuous thrusting that is constrained to a direction normal to the instantenous velocity vector.Energy is a conserved quantity as a consequence of this choice of thrust direction.The sine of the flight direction angle is shown to satisfy a first-order linear ordinary differential equation.This result holds for arbitrary potential functions.An interesting corollory is that an effective potential function can be described for a single degree-of-freedom equivalent system.

Acknowledgement:The results of this work were supported in part through a grant from NASA Johnson Space Center,NNX14AK46A(Technical Manager:Dr.Chris D’Souza).

Akella,M.R.(2000):On low radial thrust spacecraft motion.Journal of Astronautical Sciences,vol.48,no.2,pp.149–161.

Akella,M.R.;Broucke,R.A.(2002): Anatomy of the constant radial thrust problem.Journal of Guidance,Control,and Dynamics,vol.25,no.3,pp.563–570.

Battin,R.H.(1999):An Introduction to the Mathematics and Methods of Astrodynamics.AIAA Education Series.

Benney,D.(1958): Escape from a circular orbit using tangential thrust.Jet Propulsion,vol.28,pp.167–169.

Hernandez,S.(2014):Low-thrust Trajectory Design Techniques with a Focus on Maintaining Constant Energy.PhD thesis,2014.

Hernandez,S.;Akella,M.R.(2015):Energy-conserving planar spacecraft motion with constant-thrust acceleration.Journal of Guidance,Control,and Dynamics,pp.1–15.

Jezewski,D.(1983): An analytic solution for the j2perturbed equatorial orbit.Celestial Mechanics,vol.30,no.4,pp.363–371.

Prussing,J.E.(1998): Constant radial thrust acceleration redux.Journal of Guidance,Control,and Dynamics,vol.21,no.3,pp.516–518.

Tsien,H.-s.(1953):Take-off from satellite orbit.Journal of the American Rocket Society,vol.23,pp.233–236.

1Professor and Myron L.Begeman Fellow in Engineering,Department of Aerospace Engineering and Engineering Mechanics,The University of Texas at Austin,Austin,TX 78712,USA.

E-mail:makella@mail.utexas.edu

2Undergraduate Research Assistant,Department of Aerospace Engineering and Engineering Mechanics,The University of Texas at Austin,Austin,TX 78712,USA.

E-mail:sofokli.cakalli@utexas.edu