屏蔽感应电机等效电路参数的有限元计算法

凌在汛 周理兵 张 毅 康惠林 王 晋



屏蔽感应电机等效电路参数的有限元计算法

凌在汛1,2周理兵1张 毅3康惠林1王 晋1

（1. 强电磁工程与新技术国家重点实验室（华中科技大学） 武汉 430074 2. 国网湖北省电力公司电力科学研究院 武汉 430077 3. 国家电网湖北省电力公司检修公司 武汉 430050）

提出了一种从有限元电磁场分析结果中准确提取屏蔽电机等效电路参数的方法。基于对2-D时谐电磁场的分析，利用傅里叶变换分析得到气隙磁通密度基波幅值并得出感应电动势的精确值。利用冻结磁导率法来计及不同转差率下的铁心饱和情况，推导出了转子外表面的坡印亭矢量表达式并据此得出传到转子侧的复功率，进而得到转子侧等效电路参数。然后，根据一台屏蔽感应电机建立有限元分析模型，将上述方法应用于该电机从而得到其等效电路参数。最后，将等效电路得到的结果与有限元分析及实验结果进行对比，验证了上述方法的准确性。

屏蔽感应电机 时谐电磁场 等效电路 坡印亭矢量

0 引言

屏蔽感应电机被广泛应用于石油、化工、航天、制冷以及核能发电等行业，具有无泄漏、低噪声和防爆等特点。近年来，该类型电机得到迅速发展，产品的研发也受到普遍重视。为提高电机的可靠性及运行性能，研究人员多采用实心转子与笼型相结合的转子结构[1]。另外，良好的控制系统还可使其高效运行于不同转速。

搭建电机控制系统需先建立电机的数学模型，而对于屏蔽感应电机来说，其电机数学模型中等效电路参数的准确计算仍然是目前研究的难点[2]。建立屏蔽感应电机的等效电路还可将电机性能与几何模型联系起来，有利于电机方案的优化设计。屏蔽感应电机如图1所示，对比常规感应电机，除转子笼型外，屏蔽感应电机还含有导电的屏蔽套。而对于实心转子电机，其导电区域还包括实心转子域。因此，屏蔽感应电机的等效电路将比常规感应电机的更为复杂。

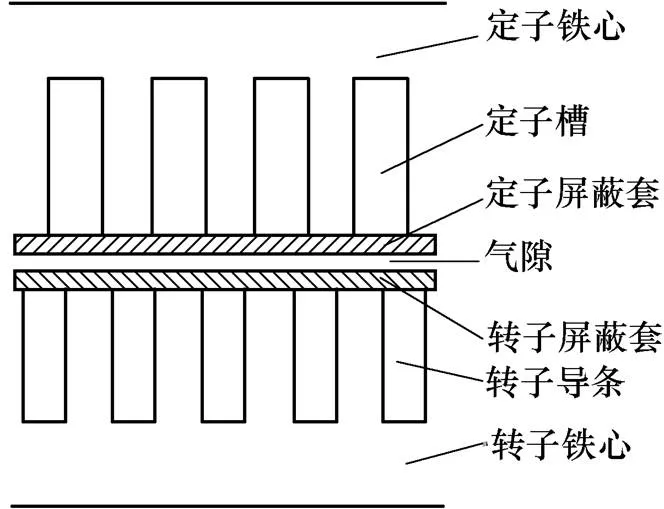
图1 屏蔽感应电机

屏蔽感应电机等效电路参数计算的常规方法采用磁路计算法[3]。然而，由于材料的非线性以及转子实心体的影响，该方法准确度有限。另外，屏蔽感应电机在不同转速下的等效电路参数也是随之变化的[4]。

随着数值分析方法的发展，基于有限元计算的电磁场分析法受到极大关注。该方法适用广泛，在电机性能分析上具有准确度高的优点。文献[5]验证了利用电磁场有限元瞬态计算结果推导电机等效电路参数的可行性。对于转子侧含有实心导体域的屏蔽电机，文献[6]采用2-D瞬态电磁场分析了屏蔽电机屏蔽套损耗，并验证了分析结果的准确性。因此，研究人员试图通过对有限元分析得到屏蔽感应电机的等效电路参数。文献[5,7,8]对2-D时谐电磁分析的结果进行处理，得到了普通感应电机等效电路参数。文献[9]建立了完整的屏蔽感应电机等效电路，包含了定转子屏蔽套、转子实心体、转子笼型的等效电阻以及等效电抗和互感抗。并通过对气隙磁通密度的分析，忽略了定、转子屏蔽套对主磁场的影响，推导出忽略定、转子屏蔽套漏电抗的简化等效电路。然而，该电路模型较为复杂且各参数准确度难以保证，不适用于控制系统。另外，该模型也无法考虑电机参数随转速变化而变化的影响。对于高转差率运行区域，由于趋肤效应的影响使得该方法准确性较差。

本文采用2-D时谐电磁场对实心转子加笼型结构的屏蔽感应电机进行了参数计算。以变频驱动下额定负载时的定子电频率作为基准频率，对该频率下转速由0到空载（0≤≤1）的不同转速稳定运行工况进行了有限元分析。提出了一种新的等效电路参数计算法，该方法通过对有限元计算结果的处理，准确计及了不同转速下因非线性铁磁材料以及趋肤效应造成的等效电路参数变化，从而得到简单实用且准确度较高的等效电路模型。最后，本文利用数值法及实验验证了新方法的有效性。

1 分析方法

1.1 有限元分析模型

对于2-D时谐电磁场，麦克斯韦方程组的复数形式可以用复数矢量磁位表示为

式中，e为将时谐电磁场中的非线性铁磁材料铁磁特性正弦化后的等效磁导率；为导电区域材料的电导率；为定子绕组电流区域电流密度；为电源频率；为感应电机转子转差率。

由于本文中的屏蔽感应电机采用了电压源作为激励，若要计算绕组电流，则还需将有限元模型与外电路进行耦合，以此来考虑端部对电机的影响。写出定子侧完整的电路方程为

对于定子侧屏蔽套、转子侧屏蔽套和转子实心体（实心转子），这三类区域都为实心导电区域。该区域的感应电流密度为

在2-D时谐电磁场有限元中，需将转子侧区域电磁场量进行频率折算，从而使得整个求解域内的电频率都为。

于是，导电区域涡流损耗矢量r可通过该区域对应的电流密度求出

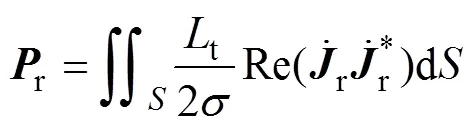
式中，为导电域截面积；“*”表示取复数的共轭；表示取复数的实部分量；为导电域的轴向电流密度。

通过将电路方程与时谐电磁场的计算有效结合的场路耦合法，保证了计算结果的完整性与准确性。

1.2 等效电路简化

为方便控制系统当中的屏蔽电机数值模型建模，本文将屏蔽异步电机的等效电路进行简化，将转子侧当作黑箱情况来考虑，其参数可由一组转子等效总漏抗与转子等效总电阻/的串联来表示，如图2所示。图中：1s为定子端部漏抗，sc为定子屏蔽套等效电阻，m为励磁电抗，0为感应电动势。

图2 简化后的屏蔽电机等效电路

1.3 等效电路参数提取

为计算不同转速下屏蔽电机的等效电路参数，本文通过将转差率由0增至1，对时谐电磁场中的屏蔽电机有限元模型进行仿真，模拟电机在基准频率下由空载到堵转整个运行区间的工作情况。

感应电动势是连接定、转子侧电路的桥梁，若要提取等效电路参数，则可先对0进行计算。通常来说，学者们多采用绕组线圈所在两槽的矢量磁位差来计算通过该绕组的磁通，进而计算0[5,8]。然而，从图3可以看出，气隙磁通密度的径向分量并非纯正弦，还含有一定阶次的高阶谐波分量。从而使得通过气隙的磁通包含了一定的高阶谐波磁通，计算结果并不准确。当转差率趋近于1时，磁通密度谐波分量更为突出，该方法得到的0与实际值之间的误差将增加。为减小计算误差，本文首先对气隙磁通密度进行傅里叶分解，然后再由基波磁通密度幅值m计算0，即

式中，1为定子绕组的每相串联总匝数；w1为绕组系数；m0为气隙磁通密度的基波幅值；ef为铁心的等效叠片长度；为极距；1为基准频率。

图3 气隙磁通密度的频谱分析结果

Fig.3 Spectrum analysis of flux density through the air-gap

于是，定子屏蔽套的等效电阻可通过0与其消耗的焦耳功率sc推导得到。

式中，为电机定子绕组相数。

由于屏蔽感应电机在不同速度稳态运行时，其铁心区域的磁饱和程度变化较大，进而使对应的电抗值（1s、m和）也将发生改变。

为了准确计算m与1s，需保证在铁心饱和情况一致的条件下对场计算结果进行处理。这里采用冻结磁导率法将上述求解工程中每一个转速下的磁导率进行冻结，导入到对应的新建工程中。

由于新建工程中铁心的饱和情况与原工程特定转速下铁心磁饱和情况相同，这就保证了新工程的定子漏抗及励磁电抗与原工程相同。在新建的工程中，对冻结磁导率之后的电机有限元模型进行空载仿真，并令绕组电阻1=0、忽略端部漏抗、所有导电实心区域电导率为零。此时，电机等效电路如图4所示。其中：1a=1，感应电动势0a可根据式（6）计算得到，于是m为

算得m后，1s的值可由图4得到，即

（9）

图4 用于电感计算的屏蔽电机等效电路简化模型

由定子传送到转子的电磁功率主要取决于坡印亭矢量的径向分量。传递到转子侧的总复功率为

式中，带下标的物理量为其在方向上的投影；i为电机转子外半径。

交流电磁场中的电磁感应定律表示为

（13）

式中，1为电机同步转速。

将式（13）代入式（11）可得

（15）

由式（15）得到的复功率并结合图2中等效电路可得

（17）

则有

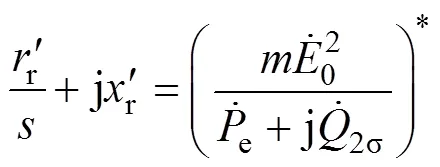
于是

（19）

2 结果分析

屏蔽感应电机等效电路参数是与转差率相关的函数。为了分析材料饱和程度、转差率以及等效电路参数间的影响关系，本文将上述的参数计算方法应用到一台屏蔽感应电机模型样机上。该电机的额定功率为200kW，额定电压N=380V，极对数=2；定子绕组采用星形联结；定子及转子都有屏蔽套，屏蔽套使用导磁且导电材料制作；转子为实心转子加用以改善运行性能的笼型复合结构。

对于传统的感应电机，其2-D有限元的耦合电路只需要包含电压源、定子绕组和转子笼型即可。而对于屏蔽感应电机，则还需要将实心导电域（定子屏蔽套、转子屏蔽套和转子实心体）体现在耦合电路中。

本文采用FLUX电磁场有限元计算软件进行分析，图5为本例中屏蔽感应电机2-D有限元模型所耦合的电路。由于定子、转子屏蔽套和转子实心体都属于整块导体，所以将其对应的实心导电域都用实心导体来表示并与无穷大电阻并联，以起到闭合电路并模拟实心导体在电机两端的开路状态。三相对称电压源采用三角形联结，其中AC可通过基尔霍夫电压定律（AC+AB+BC=0）自动由软件计算得到。定子绕组采用星形联结，使用软件对应的绕组部件进行模拟并串联电感来模拟端部漏电抗的影响，绕组电阻及端部电感值需先行计算得到。转子笼型由端环短接，并用图5中的专用笼型元件来模拟并对导条数、端环电阻及漏感值进行设置。

图5 屏蔽感应电机有限元模型耦合电路

2.1 感应电动势以及定子屏蔽套的等效电阻

根据模型样机建立有限元模型，求解场为2-D时谐电磁场，转子转差率设定为从0～1变化，即模拟电机由空载至堵转不同转速下的稳态工况。

处理不同转差率的各工况下气隙磁通密度径向分量的曲线图，对之进行傅里叶分析得到气隙磁通密度基波幅值，如图6a所示。根据式（6）得到如图6b所示的感应电动势随转差率的变化曲线。从该曲线可以看出，由于转子磁场的去磁作用以及磁饱和，使得感应电动势随着转速的降低而降低。

图7为定子屏蔽套等效电阻sc随转速变化的曲线。由于采用了导电不导磁的材料，该区域不存在磁饱和现象。又因磁场穿透深度远远大于该区域厚度，故sc的值并不随转速的变化而发生明显改变。

（a）气隙磁通密度幅值

（b）感应电动势

图6 气隙磁通密度幅值及感应电动势

Fig.6 The amplitude of flux density in air-gap and the EMF

图7 定子屏蔽套等效电阻rsc

2.2 定子漏抗及励磁电抗

图8a为1s随转差率的变化曲线，图8b为m随转差率的变化曲线。对结构及绕组方案既定的电机，影响电抗值的最主要因素就是铁心的饱和程度。

2.3 转子侧等效电路参数

图9为电机经气隙传递到转子消耗的有功功率及无功功率随转差率的变化关系。由于该模型电机采用了实心转子加导电、导磁屏蔽套结构，而采用该结构的电机在不同转差率下的转子阻抗角基本保持不变（2/2=tan≈constant）[11]。因而，当转差率接近于0时，的值将随着/的值增加而增加，如图10所示。至此，屏蔽感应电机的电路参数都已求解完毕。

（a）定子漏抗1s

（b）励磁电抗m

图8 定子漏抗以及励磁电抗

Fig.8 Thestator leakage reactance and the excitation reactance

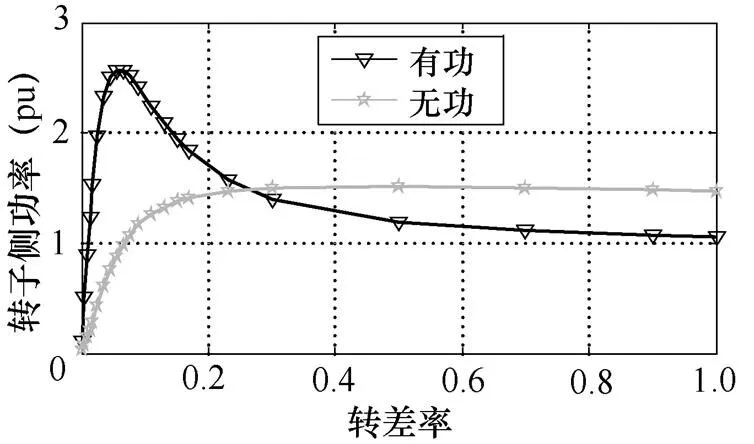
图9 转子侧消耗的电功率

图10 转子侧等效漏抗及等效电阻/s

3 结果验证

为验证上述结果的准确性，本文将由上一环节中得到的等效电路参数而建立的等效电路进行计算，并与有限元计算以及实验结果进行对比。图11为等效电路得到的定子电流、功率因数、感应电动势以及定子屏蔽套损耗与有限元计算得到运行性能对比图，图11中也针对相电流及功率因数进行了实验对比。

（a）定子相电流

（b）功率因数

（c）感应电动势

（d）定子屏蔽套损耗

图11 对比结果

Fig.11 Comparison results

由图11可知，在低转差率区间，本文用新方法建立的等效电路模型具有较高的准确度；在高转差率区间，该模型与有限元得到的结果间的差值增大，但也在10%以内。

需要注意的是，图11的电流对比中等效电路模型与实验值间的吻合度较有限元模型更好，但并不能推出本文的等效电路较有限元模型准确度更高。这是因为本文的出发点是通过对电机电磁场有限元计算结果的处理，得到准确度较高的等效电路参数。因此，等效电路的准确度依赖于有限元模型的准确性。在堵转实验时，由于实验过程中因堵转电流而产生的热量无法及时散发，使得导电区域温度急剧增加，等效电阻增大，因而使得实测相电流比未加入温度修正的有限元模型计算值要小。

4 结论

本文提出了一种屏蔽感应电机参数计算方法，利用傅里叶分析、冻结磁导率和求解坡印亭矢量等方法提高了参数计算准确度。基于流入转子侧复功率的准确计算，该方法不但能分析实心转子电机的集总参数，还可分析带有改善性能的笼型槽结构的异步电机参数。由于该方法可准确考虑铁心材料的饱和情况，不同转速下的稳态参数都能被准确计算。设计人员可根据该方法建立变参数的屏蔽电机控制模型，在不事先制造出样机并测试参数的前提下用于对控制系统的仿真及设计，这就使得研发成本降低且缩减了研发周期。

参考文献：

[1] 杨通. 笼型实心转子屏蔽电机电磁场有限元分析与计算[M]. 武汉: 华中科技大学, 2006.

[2] 徐奇伟, 宋立伟, 崔淑梅. 感应电机矢量控制中转子参数自适应辨识[J]. 电工技术学报, 2011, 26(6): 81-87.

Xu Qiwei, Song Liwei, Cui Shumei. Induction motor vector control based on adaptive identification of rotor parameters[J]. Transactions of China Electro- technical Society, 2011, 26(6): 81-87.

[3] 马宏忠. 感应电动机电感参数的准确工程计算及谐波的影响[J]. 电工技术学报, 2004, 19(6): 63-68.

Ma Hongzhong. Accurate engineering calculation of induction motor inductances and the effects of space harmonics[J]. Transactions of China Electrotechnical Society, 2004, 19(6): 63-68.

[4] Boglietti A, Cavagnino A, Lazzari M. Computational algorithms for induction motor equivalent circuit parameter determination-part I: resistances and leakage reactances[J]. IEEE Transactions on Indu- strial Electronics, 2011, 58(9): 3723-3733.

[5] 王伟华, 王红宇, 许国瑞, 等. 基于时步有限元的抽水蓄能电机瞬态参数计算方法的对比[J]. 电工技术学报, 2015, 30(1): 90-97.

Wang Weihua, Wang Hongyu, Xu Guorui, et al. Contrastive study on calculation methods of transient parameters of pumped storage machine based on time-stepping finite element method[J]. Transactions of China Electrotechnical Society, 2015, 30(1): 90-97.

[6] Liang Yanping, Hu Yonglu, Liu Xin, et al. Calculation and analysis of can losses of canned induction motor[J]. Transactions on Industrial Elec- tronics, 2014, 61(9): 4531-4538.

[7] Ling Zaixun, Zhou Libing, Guo Siyuan, et al. Equivalent circuit parameters calculation of induction motor by finite element analysis[J]. IEEE Transa- ctions on Magnetics, 2014, 50(2): 833-836.

[8] Wang Xiuhe, Zhu Changqing, Zhang Rong, et al. Performance analysis of single-phase induction motor based on voltage source complex finite-element analysis[J]. IEEE Transactions on Magnetics, 2006, 42(4): 587-590.

[9] Ergene L T, Salon S J. Determining the equivalent circuit parameters of canned solid-rotor induction motors[J]. IEEE Transactions on Magnetics, 2005, 41(7): 2281-2286.

[10] 汤蕴璆, 梁艳萍. 电机电磁场的分析与计算[M]. 北京: 机械工业出版社, 2010.

[11] 程明, 周鹗. 复合实心转子磁阻电机转子阻抗的解析计算[J]. 电工技术学报, 1991, 14(4): 16-20.

Cheng Ming, Zhou E. Analytical calculation of the impedance of composite solid rotor of reluctance motors[J]. Transactions of China Electrotechnical Society, 1991, 14(4): 16-20.

Parameters Calculation of Canned Solid-Rotor Induction Motor by Finite Element Analysis

1,21311

（1. State Key Laboratory of Advanced Electromagnetic Engineering and Technology Huazhong University of Science and Technology Wuhan 430074 China 2. State Grid hubei Electric Power Research Institute Wuhan 430077 China 3. State Grid Corporation of China in Hubei Electric Power Company of Maintenance Company Wuhan 430050 China）

This paper presents an accurate calculation method to extract parameters of canned solid-rotor induction motor from finite element analysis of electromagnetic field. The 2-D time-harmonic application is used in the accurate simulation. The Fourier analysis method is applied to obtain the basic wave of air-gap flux density, and the then electromotive force is further calculate. The frozen permeability method is also used to take the iron saturation into consideration in whole operating range. The Poynting-vector in the edge of rotor region is derived to get the value of complex power flowing into the rotor side, and the equivalent parameters of rotor can be further determined. Finally, the proposed approach is verified by both numerical and experimental solutions.

Canned solid-rotor induction motor, time-harmonic field, equivalent circuit, Poynting- vector

TM32

2014-09-19 改稿日期 2015-04-01

凌在汛 男，1989年生，博士，研究方向为电机性能优化及新型电机开发。E-mail: lingzaixun@163.com（通信作者）

周理兵 男，1961年生，教授，博士生导师，研究方向为新型电机的运行理论及其控制。E-mail: zlb@mail.hust.edu.cn