黑潮末端与黑潮延伸体的流场异常模态分析*

卢 姁，徐 建，卢 艳，张 铭

(1.中国人民解放军 61741部队，北京 100094;2.解放军理工大学 气象海洋学院 大气环流与短期气候预测实验室，江苏 南京 211101；3.北京市计量检测科学研究院，北京 100029)



黑潮末端与黑潮延伸体的流场异常模态分析*

卢 姁1，2，徐 建1，2，卢 艳2，3，张 铭2

(1.中国人民解放军 61741部队，北京 100094;2.解放军理工大学 气象海洋学院 大气环流与短期气候预测实验室，江苏 南京 211101；3.北京市计量检测科学研究院，北京 100029)

对北太平洋黑潮末端及黑潮延伸体的流场异常采用复EOF分析，结果发现：该海域流场明显异常在全年四季都主要发生在黑潮末端和黑潮延伸体上，其异常的主要形式在前2个模态均表现为一条由中尺度涡旋组成的涡旋带，带上通常有两两旋转方向相反的涡旋偶。各季第一模态方差贡献表现的季节变化特征与日本以南的黑潮流量相一致，秋季最大，夏季次之。ENSO的机制是副热带太平洋经圈环流与热带太平洋纬向环流系统之间的相互作用，其在各季第一模态的年际变化上均有所反映。冬季PDO在年代际变化上表现明显，其他三季则NPGO表现明显。该海域流场异常的性质是海洋Rossby波的异常，而赤道太平洋流场异常的性质是赤道俘获波的异常，但两者均与风应力异常强迫有关。

流场异常；黑潮末端；黑潮延伸体；复EOF分析

黑潮是位于北太平洋西侧的一支西边界流，具有高温、高盐、流幅窄、流速快、流量大等特征。日本列岛以南的黑潮通常称之为黑潮末端。黑潮延伸体是指太平洋西边界流在140°E，35°N附近与日本海岸分离后进入北太平洋的水体，其呈现2个大弯曲形态，体现了“蛇曲”的现象，且各年弯曲程度和弯曲位置均有较明显的季节变化。黑潮延伸体的主轴南北两侧都有涡旋分布,这些涡旋各年也存在季节变化，在春季较弱，夏季最强，秋末冬初较强。在离开日本海岸后，黑潮延伸体的流量增加，不稳定性增强，因此该区域是海洋中尺度涡旋最活跃的区域之一[1-2]。分析表明，黑潮末端和黑潮延伸体所在的海域是北太平洋流场异常最明显的海域[3]。

卫星高度计资料目前已得到广泛应用，黑潮末端和黑潮延伸体所在海域也成为研究的热点海域；学者利用该资料分析了该海域的SSH和SSHA，以了解流和中尺度涡旋及其异常的结构和演变，探讨了其季节和年际变化，并得到了很多有意义的结果[4-6]。在准地转的框架下，海表流场及其异常的结构虽可由SSH和SSHA推得，然而毕竟不是直接的流动图像，很难用于表层之下的上层海洋；此外，目前卫星高度计资料的时段还不长，不能讨论年代际变化。目前，在该海域，除利用卫星高度计资料进行研究外，利用SST资料在这方面所做的研究也很多[7-8]，但SST受辐射、感热等热力因子的影响，其与流场的关系较复杂。次表层海温与流场的关系较SST要单纯，因其排除了热力因子，故目前很多研究已转到利用次表层的海温资料上来[9-10]。在该海域采用年代较长且较可靠的海洋上层流场资料，对黑潮末端和黑潮延伸体的流场和中尺度涡旋直接开展研究，则可弥补卫星高度计资料的不足，并特别有助于开展年代际变化的研究，但有关的研究尚不多见。

年代际气候变率已成为全球气候中的热点问题。太平洋海气系统既有最强的年际信号，也存在明显的年代际变化。研究表明，太平洋年际变化优势区位于热带太平洋，而年代际变化优势区位于中纬北太平洋，包含了黑潮末端和黑潮延伸体海域[11]。Mantua等把这种太平洋年代际振荡现象称为PDO(Pacific Decadal Oscillation)[12]。PDO可以用北太平洋SSTA的EOF第一模态来表征。目前关于PDO已有大量研究成果[13-14]。然而PDO还不能解释东北太平洋中盐度、营养物质、含氯量及鱼储量等的年代际变化。为此，2008年Di Lorenzo定义了一个新的气候模态NPGO (North Pacific Gyre Oscillation)[15]，NPGO是东北太平洋SSHA的EOF分解第二模态，因其与SSTA的EOF分解第二模态有很好相关[16]，故也可用SSTA的EOF第二模态来表征。PDO和NPGO是北太平洋2个主要的气候模态。

因此，本文采用较可靠的海洋流场资料，对黑潮末端和黑潮延伸体海域的流场做了复EOF诊断，分析了其第一、二模态的空间场和时间系数，以便探讨黑潮末端、黑潮延伸体和中尺度涡旋流场异常的结构，给出其年际特别是年代际变化,并对各模态与ENSO、PDO和NPGO的关系做了讨论。

1 资料和诊断方法

本文所用的资料为美国UMD的SODA 2.2.4逐月全球海洋同化分析资料[17](http://soda.tamu.edu/assim/SODA_2.2.4/)，该资料提供了1871-2008年深度在5～5 375 m共40层上的各月平均洋流，网格距为0.5°×0.5°。此前我们曾用该资料对1951-2008年共58 a的赤道外北太平洋上层洋流的异常做过分析[3]；分析中所取的海洋深度为：112，96，82，70，57，46，35，25，15，5 m，因为此10层上资料的可靠性较好。分析发现，北太平洋流场异常明显的海域位于(27°15′～39°45′N， 134°15′～154°45′E)，该海域中包含了黑潮末端与黑潮延伸体以及中尺度涡旋，且将该海域称之为关键区[3]。本文研究的范围就取此关键区，而时间段也取1951-2008年。

为揭示此关键区内的全年上层洋流的异常规律，本文对各月该洋流异常做了复EOF分析，其原理可参见文献[18-19]，本文不再赘述。具体操作步骤：首先对上述10个深度上的各年各月平均流场按月求其58 a的平均值，将各年的各月平均流场相应减去该平均值，则可得各年各月这10层上的偏差流场；然后将各月这10层上的偏差流场作为一个整体进行复EOF分析，这样各层有相同的时间系数，这也是该复EOF分析方法的特色和优点。此时各月各EOF模态的空间场和时间系数场都是复数；各月空间场的模表示各月各模态流场异常的流速大小，辐角则表示其流向；而时间系数表示这58 a中各月流速、流向随年份的变化。

本文主要讨论区域深度为112和15 m的2层。前者是本文所取的最深层次，在该深度海温变化已很难受到辐射、感热等热力因子影响；其主要由海水的垂直运动来决定，上升处有降温，下沉处有增温，此即为海温的动力变化。在以上10层中，因前者处于次表层水团中，以下为叙述方便，就直接称其为次表层(次表层水是在大洋表层之下，以跃层为界形成的水团，其厚度通常为200～300 m)；而后者可称之为近表层。

2 诊断结果分析

复EOF分析的结果表明，所得到的前2个模态都通过了显著性检验[20]。各月第一、二模态的方差贡献见表1，前者的各月平均为21.4%，是最重要的模态，后者为13.5%，仍具重要性。本文以下仅给出第一、二模态的结果并进行讨论。

由表1还可见，第一模态在秋季(9-11月)的方差贡献最大，夏季(6-8月)次之，冬季(12月至翌年2月)最小；第二模态在夏季最大，秋季次之，冬季最小。夏季和秋季的流场异常要比冬季和春季显著(参见表1中累计方差一栏)。研究表明[21]，日本以南(137°E断面)的黑潮流量表现出秋季最大，夏季次之的季节特点，且1—7月的流量较年平均流量要偏小，而8—12月的则偏大。这与第一模态的方差贡献相一致。以下分别给出1，4，7，10月份的复EOF分析结果，并分别代表冬、春、夏、秋四季。

表1 北太平洋各月各模态的方差贡献及其累计方差贡献Table 1 Variance and accumulated variance contributions of the two modes in the North Pacific in each calendar month

2.1 第一模态

在北太平洋上层，从诊断得到的各季第一模态空间场的总体分布可知：在上述10层上，明显的偏差流场出现在黑潮末端和黑潮延伸体上，表现为一条由中尺度涡旋组成的涡旋带，这些涡旋的尺度(直径)约为200～400 km，并通常两两构成旋转方向相反的涡旋偶形式；距本州岛东海岸最近的那些涡旋其强度最大，且它们的轴心呈东北西南走向，大致平行于该海岸线，在黑潮延伸体上的涡旋带则呈纬向分布(图1)。随着季节变化，上述涡旋带中涡旋的形态也有些变化，春、夏季这些涡旋的强度更大些。在这10层上该空间场的差异很小，这表明海洋上层的流场异常具有正压性，该处海水可看作是不可压缩的，为此该模态次表层的图略。

图1 近表层第一模态的空间场(m·s-1)

从各季第一模态时间系数春、夏、秋季的辐角集中在0°和±180°附近；冬季辐角分布的离散度略大，但仍集中在-50°和130°附近。这表明四季辐角的分布均大体对应于2个状态，这2个状态也可用数学符号“+”、“-“来标注。第一模态时间系数各季的模值各年也有所不同。

对于辐角分布存在2个状态的情况，可将辐角和模的这2个时间系数序列综合为一个时间序列。具体的做法是：将春、夏、秋三季每年时间系数的模值乘以该年辐角的余弦，而冬季则每年将时间系数的模乘以该年辐角加上50°的余弦。如此各年四季的余弦值均接近±1，这样对冬、春、夏、秋四季，各年均能得到一个新的实数序列，称之为实时间系数序列，该序列能综合反映辐角和模的时间演变。

此方法仅适用于时间系数的辐角分布在两个状态的情况。此时对于春、夏、秋三季，因其第一模态辐角分布在0°和±180°，故有结论：该模态各年的流向就约等于此模态空间场的流向，而其强度则由实时间系数序列值的绝对值来决定，若该序列值为负，则流向要反向。对冬季，因第一模态辐角分布在-50°和130°，故首先要对此模态空间场的流向做-50°也即顺时针50°的旋转，然后将旋转流向后的场作为新的空间场，对该新空间场，则有以上相同的结论。由于旋转角度(50°)不算太大，故该新空间场中，上述涡旋带中涡旋的数目不变，但各涡旋的散度绝对值减小而涡度绝对值增大，新空间场上中尺度涡旋表现得更明显。对于时间系数的辐角分布在3个及以上状态的情况，则不能得到实时间系数序列，此时必须要用辐角和模的时间系数序列来讨论问题。

图2为各季第一模态的实时间系数序列图。由图2可知，该序列有明显的年际变化和年代际变化。为了更准确地反映这种变化，现对各季第一模态实时间系数序列做了小波分析。图3为其小波全谱，从该图可见：冬季有约6 a的年际变化，12～13 a和18～19 a的年代际变化，并以最后者为最显著；春、夏、秋三季都有约7 a的年际变化和约15 a的年代际变化，均以后者最显著。总之，各季年代际变化都较年际变化要显著。

图2 第一模态实时间系数图

2.2 第二模态

各季第二模态的空间场分布见图4，其总体仍表现为上述涡旋带上的涡旋，但涡旋分布形式与第一模态有些不同，两者涡旋有所错位(可对照图1与图4)。第二模态与第一模态一样，各层上空间场的差异也很小，流场异常的正压性明显，因此次表层的图也略。

图3 第一模态实时间系数序列的小波全谱

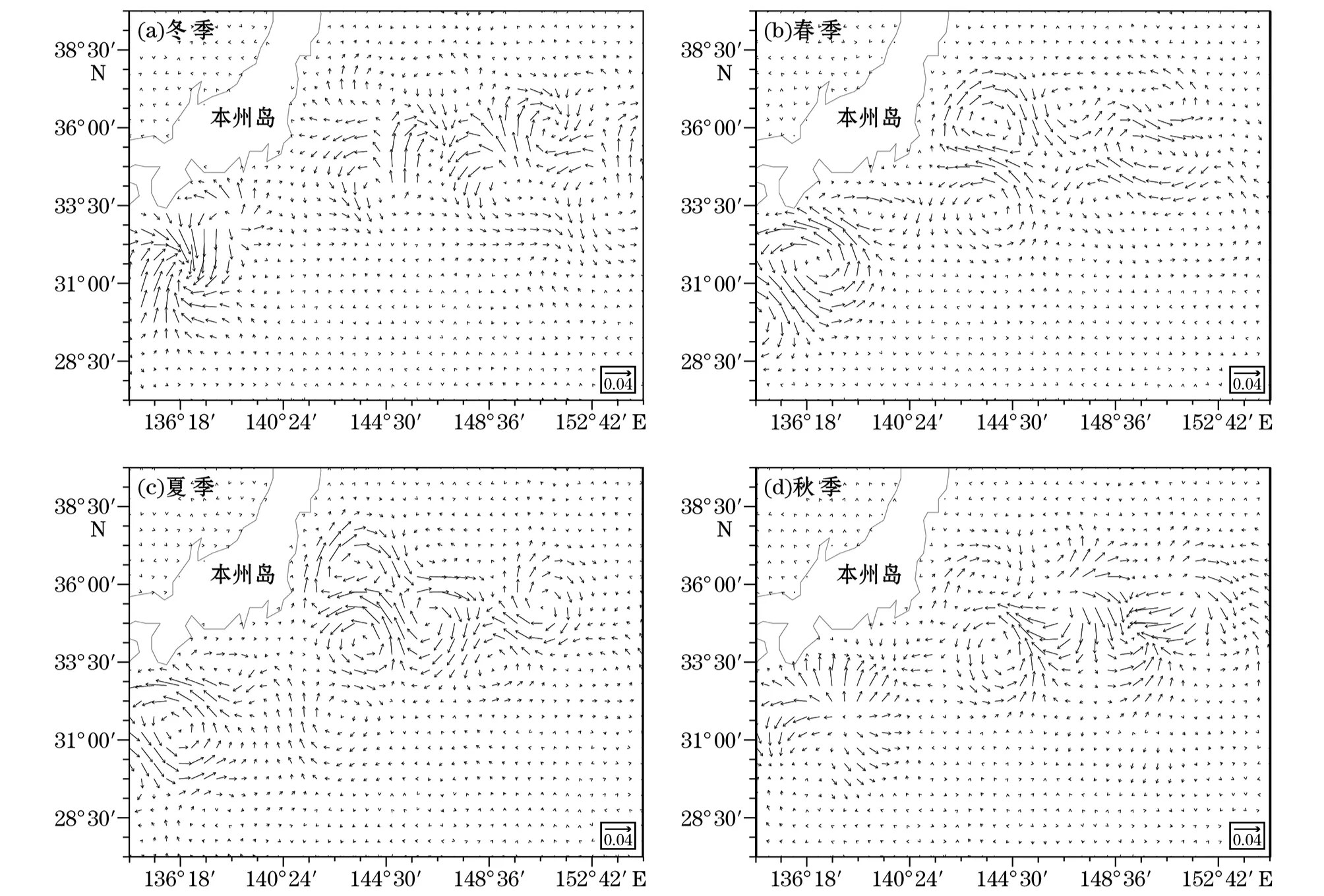
图4 近表层第二模态的空间场(m·s-1)

与第一模态相似，各季第二模态时间系数的辐角分布也有2个状态，不过其在这2个状态上分布的离散度要较第一模态大些。各季第二模态时间系数的模值大小各年也都有明显差别。采用与第一模态同样的做法，也能得到各季第二模态的实时间系数序列(图5)；对该序列也做了小波分析，并可见第二模态各季的小波全谱总体呈单峰分布，年际变化均不很显著，而年代际变化都十分显著；冬季有约20 a，春、夏、秋三季均有约15 a的年代际变化周期(图6)。

图5 第二模态实时间系数图

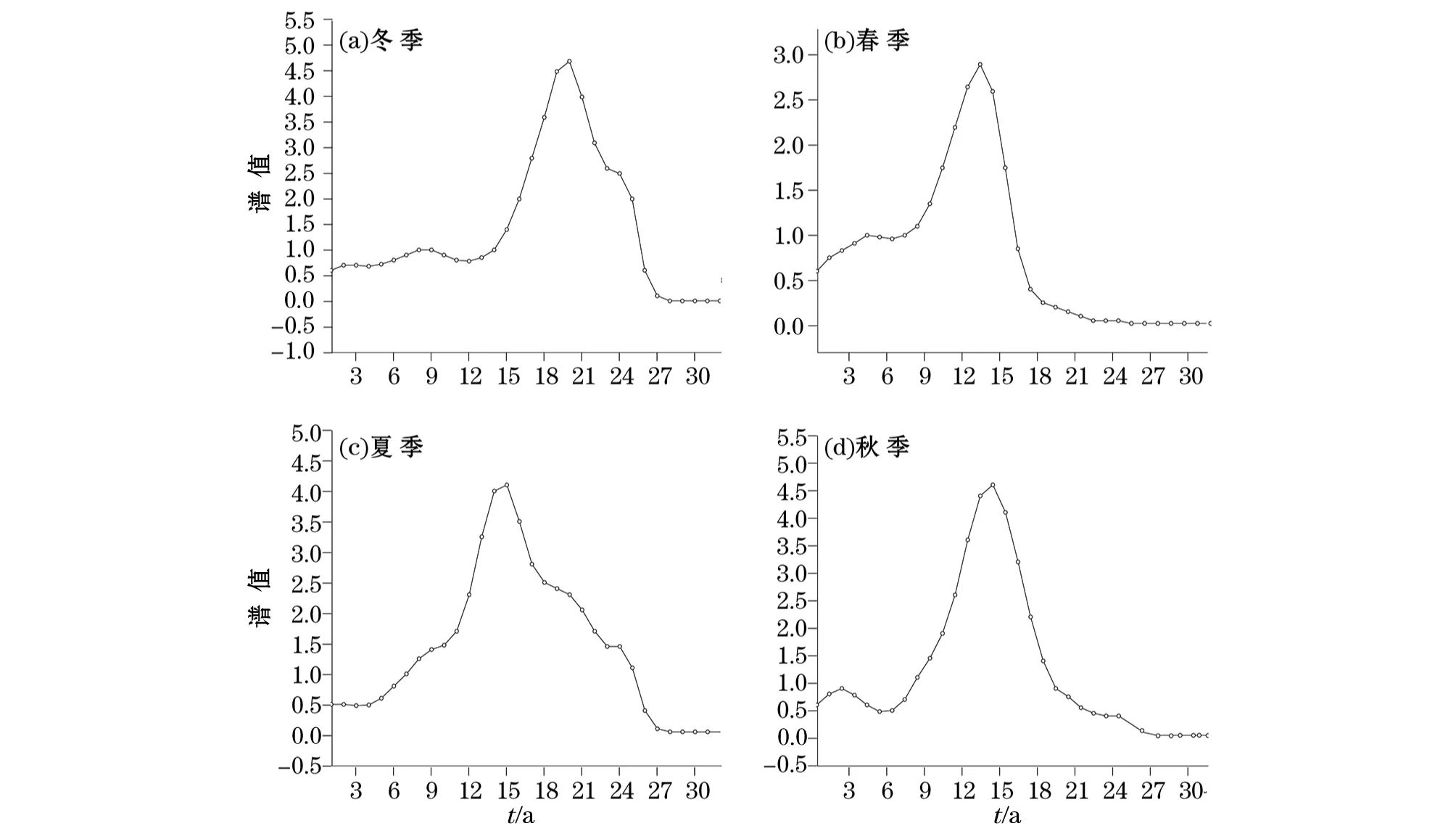
图6 第二模态实时间系数序列的小波全谱

3 有关中尺度涡旋的讨论

综上所述，黑潮末端和黑潮延伸体海域是北太平洋流场异常最明显的海域。在该海域即关键区中海洋上层58 a的各月份平均流场上可见，各月份各层次的平均流场差异都很小，因此这里仅给出1,7月(冬、夏季)近表层的平均流场图(图7)。图7中最主要的流系有3个：呈“蛇曲”(波动)状的黑潮延伸体，其波动振幅向大洋中部衰减，“蛇曲”上的两个主脊分别位于143°30′E和147°36′E，两脊之间的主槽则位于145°30′E。位于日本本州岛南面的黑潮末端。黑潮末端南侧中心在(30°18′N,135°18′E)的椭圆状反气旋涡旋，即回流涡旋。

图7 冬、夏季多年平均流场(m·s-1)图

黑潮末端和黑潮延伸体均呈现急流形式。在多年平均上，这3个系统都很稳定，冬夏变化很小。除以上回流涡旋外，冬、夏季在黑潮延伸体急流以南还有较弱的3个中尺度反气旋涡旋，中心分别位于(33°N， 142°36′E)、(33°N，148°E)、(33°N,151°36′E)附近(图7)。因该图是多年平均图，给出了中尺度涡旋分布的背景状况，各年各月的具体情况则会有所不同，这由流场异常各模态的空间场和时间系数来决定。

从各季第一、二模态的空间场可见(图1，4)，流场异常都表现为黑潮末端和黑潮延伸体上的涡旋带处，在该带之外流场异常小，在该带上则多表现为旋转方向相反的中尺度涡旋偶；这表明中尺度涡旋运动是流场异常的最主要形态。比较平均流场(图7)与异常流场的第一、二模态(图1，4)可见，两者形式完全不同，前者以急流形式为主，后者则以中尺度涡旋为主，这表明各月关键区中3个流系的变化(异常)，主要由各模态中的中尺度涡旋来决定。从动能分布来看，平均场动能以急流的动能为主，而偏差场动能则以涡旋动能(Eddy Kinetic Energy, EKE)为主，也即动能异常主要由偏差场的中尺度涡旋动能来体现。

实时观测表明，在水深200 m以上，有多个中尺度涡旋分布在黑潮末端和黑潮延续体的急流两侧，并也构成带状；在此急流与涡旋并存，这是黑潮末端和黑潮延续体上的显著特点[23-24]。总体而言，这些涡旋在春季较弱，夏季最强，秋末冬初较强。需注意的是，以上特点看来与四季第一、二模态的空间场有些类似，但在该空间场上出现的那些涡旋是复EOF分析的结果，反映了该处的流场异常；故与观测的结果不能混淆。不过观测场的多年平均就是气候平均场(背景场)，而各模态空间场则是该背景场的偏差(异常)，故两者分布有些类似是很自然的。因观测和复EOF得到的中尺度涡旋(两者合称为前者)都分布在黑潮末端和黑潮延伸体(这两者合称为后者)急流两侧，故前者的涡旋动能应与后者密切有关；至于前者产生的原因，有学者认为与后者上急流的正、斜压不稳定有关，为背景流的失稳所导致[25-26]，此外风应力的强迫也是前者产生的原因之一[27]；本文复EOF的诊断结果表明，各模态流场异常的正压性明显；且后者呈急流形式(图7)，满足正压不稳定的必要条件，故而支持正压不稳定的说法，当然也不排除上述其他原因；至于这些原因中何种是最主要的则有待于更深入的研究。

第一、二模态中主要表现为中尺度涡旋形式的流场异常，其仍是准地转的，这是由于其水平尺度L为100 km，其流速尺度U为1 m/s，取地转参数f=10-4s-1，则其Rossby数R0=U/(fL)=0.1≤1的缘故；还可知，其出现在一条涡旋带中，而此带处于气候平均的黑潮末端和黑潮延伸体的急流上(将图1，4与图7做比较)；如此则其主要体现了该急流的异常。可认为该急流是由海底地形导致的海洋Rossby波[28](这与大气中气流过山形成的大气Rossby波相类似)，故其反映了该海洋Rossby波的异常。

4 各模态的年际和年代际变化

4.1 季节与年际变化

各模态的季节变化比较明显，这体现在各模态四季的空间场上涡旋带中的涡旋分布都不相同。以第一模态冬、夏(1，7月)为例，两者空间场上最大的不同在于冬季在本州岛以东海域(33°30′N以北,144°30′E以西)有2个旋转方向相反的中尺度强涡旋，组成涡旋偶，在本州岛以南海域有1个中尺度强涡旋；而夏季在该岛以东的该海域只有1个中尺度强涡旋，在该岛以南则有2个旋转方向相反的中尺度强涡旋，并组成涡旋偶。造成这种状况的原因是在冬、夏的风向异常两者不同，前者主要为偏西风异常，后者主要为偏南风异常。

在年际变化上，黑潮延伸区的海平面异常和海表面温度异常的低频分量与Nino3指数具有较高的相关性[29]，而各季第一模态大致都有6～7 a的明显年际变化，其中夏、秋两季更要显著(图3c，3d)，这应是ENSO在年际变化上的反映。以上结果表明黑潮末端和黑潮延伸体流场的年际变化参与了ENSO循环，而黑潮与热带太平洋纬向环流系统间的相互作用是沟通ENSO循环的内在环节[30]。第二模态实时间系数小波全谱图中年际变化则不如第一模态明显，这说明ENSO对该模态影响较第一模态要小。

4.2 年代际变化

第一模态冬季有约20 a的最强年代际变化周期。其与北太平洋年代际涛动(PDO)的周期相同，应为PDO在流场异常上的反映[31]，而冬季阿留申低压也最强大。约15 a的年代际变化在各季都很明显，除冬季外，在小波全谱图上该周期成为主峰，特别在夏秋季表现则更突出。该约15 a的周期则与NPGO约13 a的周期很接近，应为NPGO在流场异常上的反映，并与副热带太平洋环流有关[32]，而该环流在夏季强度最强，位置也最偏北。

在年代际变化上，各季第二模态也有约20 a的周期，也应为PDO在流场异常上的反映。除冬季外，其他三季最明显的年代际变化同样约为15 a，为NPGO在流场异常上的反映。因NPGO与SSHA与SSTA的第二模态有关[15-16]，对于气候尺度，表层流场异常与SSHA有准地转关系，在一定条件下与SSTA也有诊断关系[7,32]。既然SSHA与SSTA的第二模态能反映NPGO，则除冬季外流场异常的第二模态反映了NPGO也很自然。冬季因阿留申低压十分强大，且位置偏南，故NPGO为PDO所掩盖，在小波全谱图上约15 a的周期则成为次高峰。

以上对第一、二模态的分析表明，黑潮末端和黑潮延伸体海域(关键区)的年代际变化与北太平洋流(North Pacific Current, NPC)以及该流以北的阿拉斯加环流(Alaskan Gyre)和以南的副热带环流(Subtropical Gyre)的异常有关；该两个环流的异常又分别与大气中的阿留申低压异常和太平洋副热带高压异常有关，而它们之间的海气相互作用应是造成PDO和NPGO的原因。本文的关键区则抓住了这些流动的关键部分。综上，冬季第一模态为PDO的主模态，第二模态为PDO的次模态，其他季节第一模态为NPGO的主模态，第二模态为NPGO的次模态。

前面已发现日本以南的黑潮流量与第一模态方差贡献的季节变化特征相一致，根据Sverdrup等[33]、Munk[34]和Stommel[35]提出的有关均质海洋的风生海洋环流理论，作为北太平洋副热带环流中的西边界流黑潮，其流量由北太平洋副热带海面风应力旋度所决定。研究表明[13,36]，年代际振荡的时间尺度取决于副热带海洋环流的调整时间，而后者的缓慢调整涉及两个物理过程，一个是大气风应力旋度强迫产生的海洋Rossby波向西传播，在若干年后到达西边界，从而影响副热带环流西边界流的向极输送以及向黑潮末端和黑潮延伸体的热量输送；另一个是副热带环流对温度的平流输送过程[37]。

5 北太平洋与热带太平洋洋流异常的比较

文献[38]中我们研究了热带太平洋上层洋流异常(前者)，这里将前者与北太平洋黑潮末端和黑潮延伸体海域(关键区)的上层洋流异常(后者)作一比较；从明显异常的纬向范围看，前者异常分布在整个赤道太平洋海域，范围较后者要大。从异常的性质看，前者是海洋赤道波动(含Kelvin波)的异常，其表现为赤道俘获波的形式；而后者上面已论及，有R0≤1，是准地转的，并是海洋Rossby波的异常，该异常表现为中尺度涡旋的形式。

该两者虽有以上不同之处，但也有共同的地方，即这两者异常则均与风应力异常密切有关。有研究表明，中纬度风应力旋度强迫的海洋Rossby波西传到太平洋西边界可能和向赤道传播的海岸Kelvin波耦合，从而使中纬度信号与热带信号相关联[39-40]，这就将本文对北太平洋关键区的研究与以前对热带太平洋的研究联系到一起了，同时这也说明了本文第一模态的年际变化受ENSO影响大的原因。

6 结 语

本文采用复EOF分析方法，对全年四季北太平洋黑潮末端和黑潮延伸体海域(关键区)的海洋上层流场异常做了统计动力诊断，得到了以下主要结论：

1)各季该海域上层流场的明显异常主要发生在黑潮末端和黑潮延伸体上即关键区中，其异常的第一、二模态均表现为一条由中尺度涡旋组成的涡旋带，带上通常有两两旋转方向相反的涡旋偶，这是该流场异常的主要形式。

2)第一模态在秋季的方差贡献最大，夏季次之，冬季最小；第二模态则在夏季最大，秋季次之，冬季也最小；各季第一模态方差贡献表现的季节变化特征与日本以南的黑潮流量相一致。

3)在第一模态的年际变化上，ENSO在各季均有所反映，其机制是副热带太平洋经圈环流与热带太平洋纬向环流系统之间的相互作用；而第二模态ENSO的影响不大。

4)在年代际变化上，冬季PDO表现明显，其他三季NPGO表现明显；冬季第一模态为PDO的主模态，第二模态为PDO的次模态，其他三季第一模态为NPGO的主模态，第二模态为NPGO的次模态。

5)以上两模态异常的性质是海洋Rossby波的异常，这与赤道太平洋是赤道俘获波(含Kelvin波)的异常不同，但两者则均与风应力异常强迫有关。

最后要说明的是，本文主要工作是进行诊断分析，对造成异常的动力学原因涉及不够，这是本文局限所在，也是今后要做的工作。

[1] QIU B, CHEN S, HACKER P, et al. The Kuroshio extension northern recirculation gyre: Profiling float measurements and forcing mechanism[J].Journal of Physical Oceanography,2008,38(8):1764-1779.

[2] SCHARFFENBERG M G, STAMMER D. Annual variations of geostrophic currents and eddy kinetic energy inferred from TOPEX/Poseidon and Jason-1 tandem mission data[J].Ocean Sciences Meeting, Orlando,2008:3-7.

[3] LU K C, LU X, ZHANG M. Analysis for upper abnormal current in North Pacific without equatorial area[J].Marine Science Bullent, 2011, 30(1): 29-36. 路凯程,卢姁,张铭.赤道外北太平洋上层洋流异常分析[J].海洋通报,2011,30(1):741-748.

[4] DBCHELTON D B, SCHLER M G, SAMELSON R M. Global observations of nonlinear mesoscale eddies[J].Progress in Oceanography,2011,91(2):167-216.

[5] TAGUCHI B, QIU B, NONAKA M, et al. Decadal variability of the Kuroshio extension: Mesoscale eddies and recirculations[J].Ocean Dynamics,2010,60(3):673-691.

[6] ZHANG Y C, ZHANG L F, WANG Y G. Interannual sea level variability in the North Pacific Ocean and its mechanisms[J].Journal of Geophysics, 2010, 53(2): 247-255. 张永垂,张立凤,王业桂. 北太平洋海表面高度的年际变化及其机制[J].地球物理学报,2010,53(2):247-255.

[7] LÜ Q P, LU K C, ZHANG M. NPGO mode of the upper sea temperature anomalies in the North Pacific during winter[J].Climatic and Environmental Research, 2013, 18(2): 210-220. 吕庆平,路凯程,张铭.北太平洋冬季上层海温异常的NPGO模态[J].气候与环境研究,2013,18(2):210-220.

[8] WANG L, LI T, ZHOU T J. Interseasonal SST variability and air-sea interaction over the kuroshio extension region during boreal summer[J].Journal of Climate,2012,25(5):1619-1634.

[9] WU H Y, LI C Y. The preliminary reseach of equatorial Pacific-Indian Ocean temperature anomaly mode and subsurface ocean temperature anomaly[J].Acta Oceanologica Sinica,2009,31(2):24-33. 吴海燕,李崇银.赤道太平洋-印度洋海温异常综合模与次表层海温异常[J].海洋学报,2009,31(2):24-33.

[10] XU K, ZHU C W. Estimation of the total dust column and dry eeposition flux over the Yellow Sea, China based on shipboard sun photometer measurements:case study[J].Atmospheric and Oceanic Science Letters,2010,3(2):106-110.

[11] GIESE B S, CARTON J A. Interanuual and decadal variability in the tropical and midlatitude Pacific Ocean[J].Journal of Climate,1999,12(12):3402-3418.

[12] MANTUA N J, HARE S R, ZHANG Y, et al. A Pacific interdecadal climate oscillation with impacts on salmon production[J].Bulletion of the American Meteorological Society,1997,78(6):1069-1079.

[13] YANG X Q, ZHU Y M,XIE Q, et al. Advances in studies of Pacific Decadal Oscillation[J].Chinese Journal of Atmospherice, 2004, 28(6): 979-992. 杨修群,朱益民,谢倩,等. 太平洋年代际振荡的研究进展[J].大气科学,2004,28(6):979-992.

[14] ALEXENDER M A. Extratropical air-sea interaction, SST variability and the Pacific Decadal Oscillation[M].Climate dynamics: why does climate vary? Sun D, Bryan F. Washington D C: Am. Geophys Uninon,2010:123-148.

[15] LORENZO D E. North Pacific Gyre Oscillation links ocean climate and ecosystem change[J].Geophys Research Letters, 2008,35(8):1-6.

[16] BOND N A, OVERL J E, SPILLANE M, et al. Recent shifts in the state of the North Pacific[J].Geophysical Research Letters,2003,30(23):2183,doi:10.1029/2003GL018597.

[17] CARTON J A, GRIESE B S. A reanalysis of ocean climate using simple ocean data assimilation(SODA)[J].Monthly Weather Review,2008,136(8):2999-3017.

[18] ZENG Q C. The theory of atmospheric infrared remote sense[M].Beijing: China Scientific Press,1974:160-166.曾庆存. 大气红外遥感原理[M].北京:科学出版社,1974:160-166.

[19] HUANG J Y. Statistic analysis and forecast methods in meteorology[M].Beijing: China Meteorological Press, 2000: 135-139. 黄嘉佑. 气象统计分析与预报方法[M].北京:气象出版社,2000:135-139.

[20] NORTH G R, BELLl T L, CAHALAN R F, et al. Sampling errors in the estimation of empirical orthogonal function[J].Monthly Weather Review,1982,110(7):699-706.

[21] CAI R S, ZHANG Q L, QI Q H. Character of transport variations at the source and adjacent area of Kuroshio[J].Journal of Oceanography in Taiwan Strait, 2009, 28(3): 299-307.蔡榕硕,张启龙,齐庆华.源地黑潮及其上下游流量的变化特征[J].台湾海峡,2009,28(3):299-307.

[22] LIU T, CHEN C C, MILO L. Accurate standard cell characterization and statistical timing analysis using multivariate adaptive regression splines[C]∥IEEE.Proc. Int. Symp. Quality Electronic Systems, 2015:272-279.

[23] WANG D X, FANG G H, WANG Q, et al. The tropical Pacific Ocean circulation variability and the interaction of air and sea[M]. Beijing:Ocean Press,2009:310-313. 王东晓,方国洪,王启,等. 热带太平洋环流变异与海气相互作用[M].北京:海洋出版社,2009:310-313.

[24] WATERMAN S, HOGG N G, JAYNE S R. Eddy-mean flow interaction in the Kuroshio extension region[J].Journal of Physical Oceanography,2011,41(6):1182-1208.

[25] STAURT P B, FRANK O B. A comparison of mesoscale eddy heat fluxes from observations and a high-resolution ocean model simulation of the Kuroshio extension[J].Journal of Physical Oceanography,2013,43:2563-2570.

[26] SYUART P B, RANDOLPH D W, KATHLEAN A D. Divergent eddy heat fluxes in the Kuroshio extension at 144°-148° E. Part I: Mean Structure[J].Journal of Physical Oceanography,2013,43:1533-1550.

[27] LÜ Q P, ZHANG W F, ZHANG M. Study of two-layer ocean model forced by the climate wind anomalies[J].Climatic and Environmental Research, 2013, 18(1): 124-134. 吕庆平,张维锋,张铭.两层海洋对风场气候异常响应的解析解及其讨论[J].气候与环境研究,2013,18(1):124-134.

[28] MIZUON K, WHITE W B. Annual and interannual variability in the Kuroshio current system[J].Journal of Physical Oceanography,1983,13(10):1847-1867.

[29] KRAMER W, DIJKSTRA H A. Optimal localized observations for advancing beyond the ENSO predictability barrier[J].Nonlinear Processes in Geophysics,2013,20(2):221-230.

[30] WANG D X, XIE Q, LIU Y, et al. The research progress of the Pacific decadal variability[J].Journal of Tropical Oceanoraphy,2003,22(1):76-83. 王东晓,谢强,刘赟,等.太平洋年代际海洋变率研究进展[J].热带海洋学报,2003,22(1):76-83.

[31] QIU B, CHEN S. Eddy-mean flow interaction in the decadally modulating Kuroshio Extension system[J].Deep Sea Research,2010,57(13-14):1098-1110.

[32] ZHANG L F, Lü Q P. The relationship between the npgo mode and npo mode in the north pacific during winter[EB/OL]. [2014-08-10].http://cpfd.cnki.com.cn/Article/CPFDTOTAL-ZGQX201111004045.htm.张立凤,吕庆平.冬季北太平洋NPGO模态与大气NPO模态的关系[EB/OL]. [2014-08-10]. http://cpfd.cnki.com.cn/Article/CPFDTOTAL-ZGQX201111004045.htm.模态与大气NPO模态的关系[EB/OL].[2014-08-10].http://cpfd.cnki.com.cn/Article/CPFDTOTAL-ZGQX201111004045.htm.

[33] SVERDRUP H U, JOHNSON M W, FLEMING R H. The oceans: Their physics,chemistry and general biology[M].New Jersey：Prentice Hall,Englewood Ciliffs,1942.

[34] MUNK W H. On the wind-dricen ocean circulation[J].Journal of Meteorological,1950,7(3):79-93.

[35] STOMMEL H. The westward intensification of wind-driven ocean currents[J].Trans of the American Geophys Union,1948,29(2):202-206.

[36] JASON C, FURTADO, EMANUELE DL, et al. North Pacific decadal variability and climate change in the IPCC AR4 models[J].Journal of Climate,2011,24(2):3049-3067.

[37] ROBERTSONA W. Interdecadal variability over the North Pacific in a multi-century climate simulation[J].Climate Dynamic,1996,12:227-241.

[38] LU X, ZHANG D L. A statistical diagnosis of upper-ocean currents in tropical Pacific Ocean in May[J].Journal of Tropical Oceanography,2009,28(2):22-30.卢姁,张东凌.热带太平洋5月份上层洋流的动力统计诊断[J].热带海洋学报,2009,28(2):22-30.

[39] JIN F F, KINOTO M, WANG X C. A model of decadal ocean-atmosphere interaction in the North Pacific basin[J].Geophysical Research Letters,2001,28(8):1531-1534.

[40] CAPOTONDI A, ALEXANDER M A. Rossby waves in the tropical North Pacific and their role in decadal thermocline variability[J].Journal of Physical Oceanography, 2001, 31(12): 3496-3515.

Received: September 22, 2014

Analysis of Abnormal Current in Kuroshio End and Kuroshio Extension

LU Xu1,2, XU Jian1,2, LU Yan2,3,ZHANG Ming2

(1.Unit61741,P.L.A，Beijing 100094,China;2.LaboratoryofAtmosphericCirculationandShort-rangeClimateForecastMeteorologicalCollege,P.L.A.UniversityofScienceandTechnology, Nanjing 211101, China; 3.BeijingInstituteofMetrology，Beijing 100029,China)

Anomalous circulations of four seasons in the upper layer in Kuroshio end and Kuroshio extension are studied using the complex empirical orthogonal function (CEOF) method. The results show that the anomalous circulation in the North Pacific mainly occurs in Kuroshio end and Kuroshio extension in all the seasons, with major anomalies represented by the first and the second modes with a vortex belt consisting of mesoscale eddies, which usually shows pairs of vortices rotating in opposite direction. Seasonality of variance contribution the first mode in each season is consistent with the strength of Kuroshio to the south of Japan, which is greatest in fall and secondary in summer. ENSO has influence on interannual variations of the first mode in all seasons through interactions between subtropical meridional cell and tropical zonal cell in the Pacific. In interdecadal variations, PDO's influence is obvious in winter while NPGO's is obvious in the other three seasons. The anomalous circulations represented by the two modes may be resulted from oceanic Rossby waves, which are different from those trapped waves in equatorial Pacific, but both have a close relation with anomalous wind stresses.

anomalous circulation; Kuroshio end; Kuroshio extension; CEOF

2014-09-22

国家重点基础研究发展计划项目——西北太平洋海洋多尺度变化过程、机理及可预报性 (2013CB956203)

卢 姁(1982-)，女，江苏南通人，工程师，博士，主要从事气候方面研究.E-mail: xlu2006918@163.com

(陈 靖 编辑)

P732.6

A

1671-6647(2016)01-0010-12

10.3969/j.issn.1671-6647.2016.01.002