大跨度拱桥施工期主跨缆索可靠度分析法研究

陈英，肖新辉

（1.中南林业科技大学涉外学院理工系，湖南长沙 410004；2.长沙理工大学交通科学研究院，湖南长沙 410076）

大跨度拱桥施工期主跨缆索可靠度分析法研究

陈英1，肖新辉2

（1.中南林业科技大学涉外学院理工系，湖南长沙 410004；2.长沙理工大学交通科学研究院，湖南长沙 410076）

针对大跨度拱桥施工过程中缆索安全状态评定，分析了施工期缆索抗力模型和荷载模型，采用缆索强度失效模式建立了各施工工况下缆索的可靠度功能函数，提出了缆索吊装施工过程中的可靠度分析方法；以磨刀溪特大桥缆索吊装施工为工程背景，采用蒙特卡洛抽样法计算了各吊装工况下缆索的可靠度指标，结果表明在吊装小箱梁时缆索的可靠度指标最低，吊装施工过程中缆索的可靠度指标值均高于目标可靠度值，满足施工要求。

桥梁；拱桥；缆索吊装；索力；可靠度指标

拱桥施工中缆索吊装施工方法应用较为广泛。吊装过程中缆索的安全系数是确保施工安全的关键，分析施工过程中缆索的可靠度指标尤为重要。

随着中国大跨度桥梁建设的飞速发展，施工期大跨度桥梁的可靠性研究取得长足进步。文献［1］以施工阶段的斜拉桥拉索为研究对象，结合施工监控数据，提出了施工期拉索的可靠度分析方法；文献［2］针对高墩大跨度桥梁墩身失稳问题，综合采用MATLAB数值软件和MIADS有限元分析软件提出了墩身失稳可靠度指标的隐式计算方法；文献［3］通过对不同施工阶段连续刚构桥主梁可靠度指标的求解，得到最大悬臂处可靠度指标水平最低。目前的研究仅针对斜拉桥和刚构桥，而对拱桥施工阶段缆索的可靠度鲜有研究。拱桥缆索吊装施工结构体系和工艺较为复杂，施工过程中任意结构出现安全问题都会带来严重后果。该文分析施工期缆索的抗力和荷载不确定性参数模型，建立施工阶段缆索的可靠度功能函数，研究缆索吊装施工过程中最不利工况的可靠性指标。

1 缆索施工可靠度分析方法

1.1 缆索抗力概率模型

缆索的抗力不确定性主要表现在材料抗力性能和截面面积制作误差，这两种不定性可通过随机变量KM表示。文献［4］指出随机变量KM服从正态分布，其均值和方差分别为1.00和0.035。扣索的抗力R计算模型见式（1），抗力概率模型见图1。

式中：fk为扣索材料的抗拉标准值。

图1 扣索抗力概率模型

1.2 主跨缆索的荷载模型

1.2.1 缆索的索力表达式推导

在吊装施工过程中，由钢绞线牵引骨架或箱梁节段在缆索上移动，该吊装体系的受力见图2。

图2 主跨主缆受力示意图

当缆索无吊装荷载时，缆索只承担本身自重，缆索的张力H为：

式中：q为主缆的单位重量；L为主跨计算跨径；f为缆索悬链线设计垂度。

在自重作用下缆索的伸长量ΔS为：

式中：E为材料的弹性模量；A为主缆的截面面积；n为矢跨比。

缆索自重作用下的有应力索长S为：

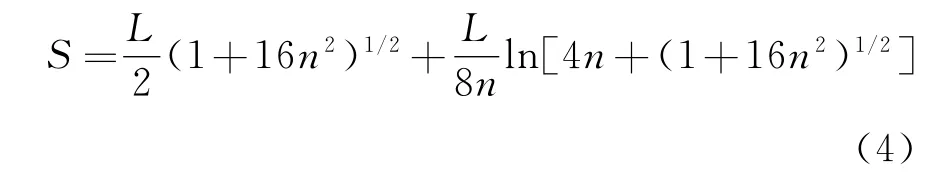
无应力索长S0为：

主跨缆索重G为：

钢绞线牵引节段移动时具有一定的动力放大，可用动力系数表示：

式中：Pg为节段的重量；η为动力放大系数；Pd为动荷载。

索的水平分力Hg为：

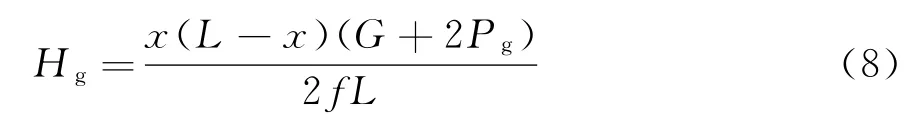
式中：x为集中力作用点距坐标原点的距离。综上，缆索索力T表达式为：

式中：V 为竖向分力；γ为缆索的水平夹角。

1.2.2 荷载参数概率模型

吊装施工过程中缆索主跨索力的表达式中部分参数具有不确定性，应以概率模型的方式进行表达。参数E、A和L均服从正态分布。其均值为材料设计值，标准正态化后的方差均为0.035。

1.3 缆索可靠性分析功能函数

假定缆索的抗力变量R与荷载变量S为相互独立的变量，则缆索的可靠度功能函数可表示为：

将式（1）、式（8）和式（9）带入式（10），得到功能函数表达式为：

鉴于施工期扣索极限状态方程的展开式较为复杂，若采用一次二阶矩法，则计算量太大，而采用蒙特卡洛抽样法求解能避免这个问题。计算过程为：1）从功能函数的所有变量模型中抽取N组变量X。2）将N组参数样本点分别带入功能函数式（7）中，统计出使功能函数Z＜0的样本组Nf，得到扣索失效概率Pf表达式［见式（12）］。3）确定抽取总样本点的数量，得到可靠度指标表达式。总抽样次数越多，则计算结果越精确。文献［4］给出了抽样推荐次数表达式［见式（13）］。式（14）为可靠度指标β的表达式。

式中：Φ-1（·）为标准累计正态分布函数的反函数。

2 工程应用实例

2.1 工程简介

磨刀溪特大桥主桥为钢管砼劲性骨架上承式拱桥，采用缆索吊装骨架节段进行施工。计算参数为：拱桥主跨径L=280 m；缆索由2×3φ56 mm2钢绞线组成，其单位重量q=1.18 k N／m；两边跨主缆与塔顶的水平夹角γ分别为14°40′和10°4′。图3为主缆吊装立面图。

图3 磨刀溪特大桥吊装系统示意图（单位：mm）

2.2 荷载工况

在吊装过程中，部分骨架或箱梁节段需从预制场沿桥梁纵向滑移至节段安装位置，施工前需进行试吊试验。如图3所示，试吊节段从A点（距离相邻塔5 m）滑移到C点（距离相邻塔5 m）。各阶段骨架的设计重量见表1，从中可知小箱梁的设计重量最大，选用最不利荷载进行试吊加载试验。

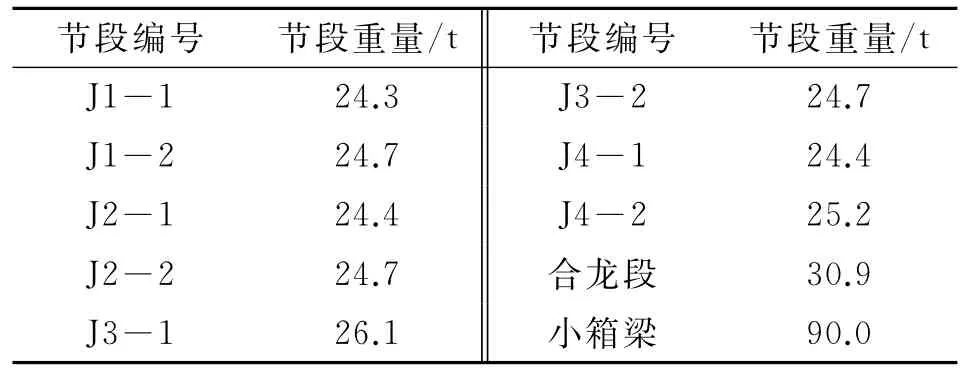
表1 磨刀溪特大桥各吊装节段的重量

为验证索力方程的适用性，选用振弦式应变传感器对索力进行测量（见图4）。试验分为3种工况：工况1为在A点处起吊构件；工况2为将构件

从A点滑移运送至B点；工况3为将构件从B点滑移运送至C点并保持静止。

图4 磨刀溪特大桥现场试吊试验索力测量

在吊装阶段，缆索承受荷载主要分为集中荷载和均布荷载。集中荷载由吊装节段重Pl=450 k N、吊具重P2=250 k N、起吊索重和牵引辅助卷扬机重P3=50 k N、平衡配重P4=50 k N组成，并考虑冲击系数1.1。主缆自重均布荷载q取1.18 k N／m。初始设计矢高f=22.4 m。

2.3 索力理论值和实测值

各缆索的索力实测值与理论值见表2。

表2 磨刀溪特大桥索力实测值与理论值对比k N

由表2可知：工况1时索力计算值与实测值的误差为22.2%。，工况2时误差为7.5%，工况3时误差为5.4%。理论计算值均大于实测值，计算偏保守，表明上述索力简化计算方法可行。

2.4 缆索施工阶段的可靠度指标

按式（10）计算各工况下缆索索力的均值和方差，结果见表3。结合式（11）和蒙特卡洛抽样法计算各施工阶段缆索的可靠度指标，结果见图5。

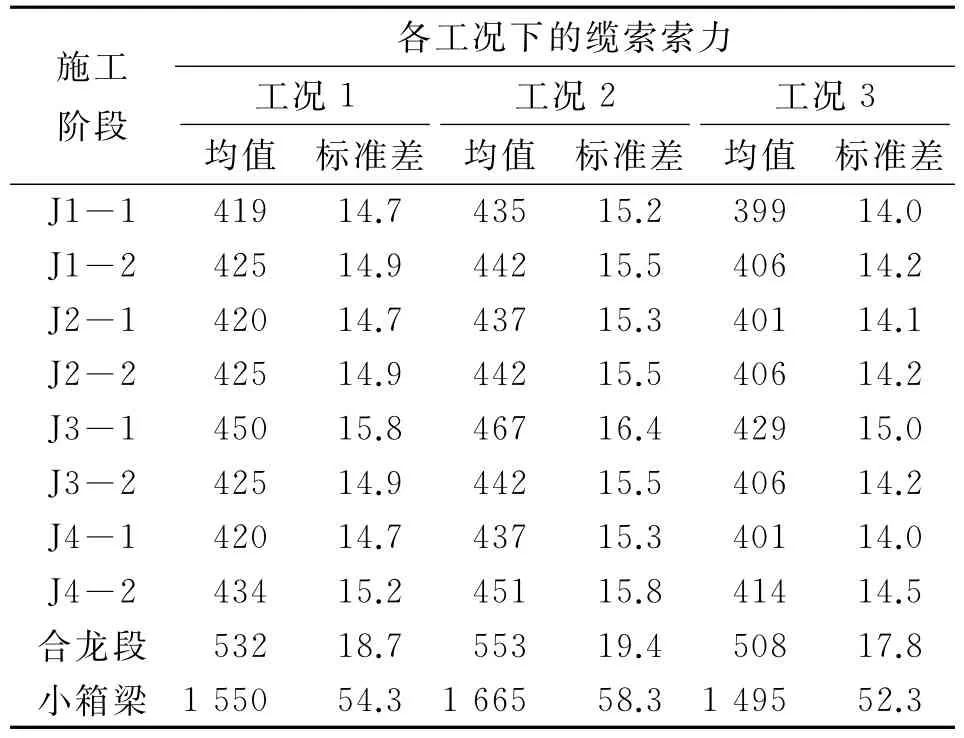
表3 磨刀溪特大桥施工全过程中的缆索索力k N

图5 磨刀溪特大桥不同施工阶段缆索的可靠度指标

由图5可知：工况2时缆索的可靠性水平普遍低于工况1和工况3。J1-1至合龙段施工时缆索的可靠度指标相对稳定；吊装小箱梁时可靠度指标最小，但仍高于目标可靠度指标值。

3 结论

该文提出了一种拱桥吊装施工过程中缆索可靠度分析方法，推导了缆索在施工过程中的索力计算表达式，分析了缆索的抗力和荷载概率模型，建立了施工期扣索的可靠度功能函数，并将该分析方法应用于磨刀溪特大桥施工过程中的缆索可靠度分析。分析结果表明，该桥吊装施工过程中缆索的可靠度指标维持在较高的状态，J1-1至合龙段施工时缆索的可靠度指标相对稳定，吊装小箱梁时可靠度水平下降明显，需关注该阶段的施工安全。

［1］ 刘扬，张建仁，李传习.混凝土斜拉桥施工期的时变可靠度计算［J］.中国公路学报，2004，17（3）.

［2］ 刘扬，鲁乃唯.钢管混凝土组合高墩连续刚构桥体系可靠指标计算方法［J］.公路交通科技，2011，28（9）.

［3］ 康浩.高墩大跨刚构桥施工期可靠度研究［D］.北京：北京工业大学，2006.

［4］ 王春生，聂建国，陈艾荣，等.基于概率断裂力学的老龄钢桥使用安全评估［J］.工程力学，2006，23（6）.

［5］ 曹珊珊，李传习.大跨度钢管砼劲性骨架拱桥施工阶段受力及稳定性分析［J］.公路与汽运，2011（1）.

［6］ 郭梁威.连续刚构桥施工期墩身稳定可靠性研究［J］.公路与汽运，2014（4）.

［7］ 刘扬，张建仁，余志武.大跨混凝土斜拉桥拉索施工期的可靠度分析［J］.中国公路学报，2007，20（3）.

U448.22

A

1671-2668（2016）06-0200-03

2016-07-23