LS-SVW／BP神经网络组合模型在GPS高程转换中的应用

毕航权，石杏喜，刘玮

（南京理工大学土木工程系，江苏南京 210094）

LS-SVW／BP神经网络组合模型在GPS高程转换中的应用

毕航权，石杏喜，刘玮

（南京理工大学土木工程系，江苏南京 210094）

传统BP神经网络在GPS高程转换中存在一定局限性，特别是在外推精度方面。为避免几何曲面模型不能贴合的情况及神经网络在训练时产生局部极小概率的问题，文中提出一种改进的BP神经网络高程异常拟合方法，即LS-SVW／BP神经网络组合模型，通过实例对该组合模型与BP神经网络、二次曲面拟合、平面拟合进行比较，说明了该组合模型用于GPS高程转换的可行性和优越性。

公路；GPS高程；LS-SVW／BP模型；高程异常

无论是在作业效率还是在测量结果可靠性方面，GPS测量技术比传统技术都取得了长足进步。但GPS测量经过平差处理后得到的是相对WG-84坐标系统的大地高HGPS，而实际工程测量得到的是正常高H0，需将大地高HGPS转换成正常高（水准高程）H0，两者之间的差值即为高程异常ξ。

常规的高程异常拟合数学模型有曲面拟合法、多项式拟合法等，都是通过拟合出与高程异常相近似的趋势面来代替拟合区域的似大地水准面。该文将LS-SVW／BP神经网络组合模型应用于GPS高程转换，并通过与BP神经网络、二次曲面拟合、平面拟合等模型进行对比说明该组合模型应用于高程转换的可行性。

1 GPS高程转换模型

1.1 最小二乘支持向量机的原理

最小二乘支持向量机（LS-SVM）是支持向量机的改进模型，秉承了支持向量机的基本思想，简化了标准支持向量机的复杂计算。它将传统支持向量机中目标函数的不等式约束改为等式约束，将误差平方和损失函数作为训练集的经验损失，把解二次规划问题转化为求解线性方程组的问题，并将经验方差的偏差的一次方改为二次方，避免了不敏感损失函数，大大降低了复杂程度，提高了求解问题的速度和收敛精度，同时使误差平方项最小化。因此，LS-SVM能解决一般SVM在样本数目多时运算速度慢、抗噪能力差、复杂等问题，在非线性预测控制方面更具优势。

给定一个有M个训练样本的集（xi，yi），i=1，2，…，M，其中训练样本为m维向量，按照结构风险最小化原则，可把函数拟合问题转换为函数约束优化问题：

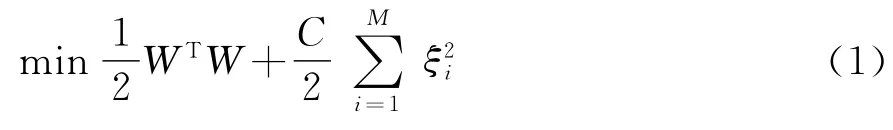
式中：W∈R为权矢量；C为正则化参数。

SVM算法中的约束条件为等式，即：

式中：g（x）为映射函数；b为偏置量。

定义拉格朗日函数：

式中：ai为拉格朗日乘子。

根据优化条件对式（3）分别求∂L／∂W、∂L／∂b、∂L／∂ξi、∂L／∂ai，并令结果为零，则有：

对式（4）进行整理后，得到LS-SVM非线性预测模型：

为了解决高维计算问题，引入核函数k（x，xi）替代g（x）g（xi），即：

1.2 神经网络法的原理

人工神经网络是由简单处理单元（神经元）按一定的方式连接而成的非线性网络，是一个大规模自适应非线性动力系统，具有集体运算能力。其中用反向传播算法进行训练的多层前向网络即为BP网络。BP神经网络具有优良的非线性逼近能力，应用也最广泛。运用BP神经网络转换GPS高程是一种自适应的映射方法，不用作假设，理论上比较合理，能避开未知因素的影响，减少模型误差，提高GPS高程的转换精度。

BP神经网络模型拟合高程的过程：1）向前传播阶段。以已知点样本集（Xi，Yi，Hi，Hri）作为学习集，将（Xi，Yi，Hi）输入，并设定阈值，计算实际的输出量Hri。2）向后传播阶段。计算输出值Hri和已知的Hri的差，按极小化误差的方式调整权值。3）工作集计算阶段。将待求样本集放入已通过前两步训练的网络中，计算拟合的正常高程。

1.3 LS-SVM和BP神经网络组合模型

虽然LS-SVM和BP神经网络各自具有很多优点，但都存在一定局限性：BP神经网络会因为初始值的取值而影响最后收敛的结果，导致模拟结果不稳定，且在一些情况下会产生局部极值问题；LS -SVM的计算精度会受到其中核函数和惩罚参数的影响。在以往研究中，有学者利用BP神经网络和二次曲面结合的模型、BP神经网络和最小二乘配置法结合的模型形成混合转换方法，并在一定工程条件下进行了试验，其原理就是利用BP神经网络来缩小二次曲面带来的曲面模型的误差。但对于面积更大，且已知控制点少的地区，这种混合转换方法的适用性还有待检验；另外，二次曲面模型与水准面是否贴合、拟合出的残差提供给BP神经网络的初始值是否准确也有待检验。

将LS-SVM和BP神经网络相结合，在不需确定几何曲面的情况下，在小样本空间中能解决训练集合产生局部极小的问题。方法（见图1）如下：

（1）在测量区域内有n1个已知点和n2个待测点，将n1个点的信息放入LS-SVM工具箱中，由此得到GPS高程异常ξ。

（2）测量出n1个已知点的高程异常ξ0，并计算其与由LS-SVM得出的异常高程之间的差值，即Δξ=ξ0-ξ。

（3）将n1个已知点的所有信息构成学习样本集（xi，yi，ξi，Δξi），其中x、y、ξ 为输入单元参数，Δξ为输出单元参数。用神经网络的方法对训练集进行训练，计算高程异常的偏差。

（4）用训练好的神经网络对n2个待测点的集合进行训练，得出各点的高程异常Δξ，进而按下式得到拟合高程：

式中：ξ为LS-SVM法中计算的高程异常值；Δξ为BP神经网络中计算的高程异常的偏差。

图1 LS-SVM／BP神经网络组合模型高程转换流程

实质上，将LS-SVM和BP神经网络相结合是为了避免几何曲面模型不贴合的情况，同时通过LS-SVM法提供给神经网络一个相对稳定的初始值，充分考虑了整体性，可减小神经网络在训练时产生局部极小的概率。采用该方法可削弱LS-SVM的整体误差，修正高程异常值，同时弥补BP神经网络在外推模型上的缺陷。

BP神经网络的输入层有一个参数ξ，输出层的高程异常偏差Δξ=ξ0-ξ即为LS-SVM在高维空间中的训练误差，ξ0为高程异常的真实值。

2 应用实例

为了分析比较平面拟合、二次曲面拟合、BP神经网络、LS-SVM及LS-SVM与BP神经网络组合模型的拟合精度，利用MATLAB编制计算程序，主要包括主界面、LS-SVM计算、BP神经网络计算、多项式曲面拟合计算、LS-SVM／BP组合模型计算和绘图6个菜单模块。主界面包括数据输入和输出。数据输入部分位于主界面的左侧，可根据点位信息情况输入，也可直接读取写字本文件中的数据。输入参数包括控制点和待测点的平面坐标及它

们的大地高、正常高。数据输出部分位于主界面的右侧，分别输出控制点和待测点的拟合高程异常和残差及待测点拟合出的正常高。点击相应的计算模块可输出对应的数值输出量，绘图模块则可绘制控制点及待测点的拟合残差图。

为了检验LS-SVM／BP神经网络组合模型的拟合效果，在南京市某标段市政道路上设置测量点，选取均匀分布的7个点（K1～K7）作为学习样本，剩下的7个点（D1～D7）作为待测点。分别采用平面拟合法、二次曲面拟合法、BP神经网络法、LSSVM法及LS-SVM／BP神经网络结合法对数据进行拟合。每个点的平面坐标、大地高、正常高及高程异常已知。

2.1 LS-SVM／BP组合模型拟合GPS高程

（1）数据的归一化处理。在进行数据拟合之前，为了避免因数据值较大而对计算结果产生影响，也为了适应BP网络的输出，减小权值调整幅度，对参与拟合运算的数据进行归一化处理，使其数值处于［-1，1］。处理方法见式（8）。归一化后已知点和待测点的坐标见表1。

式中：xi为归一化变量；xmax和xmin分别为样本集的最大、最小值。

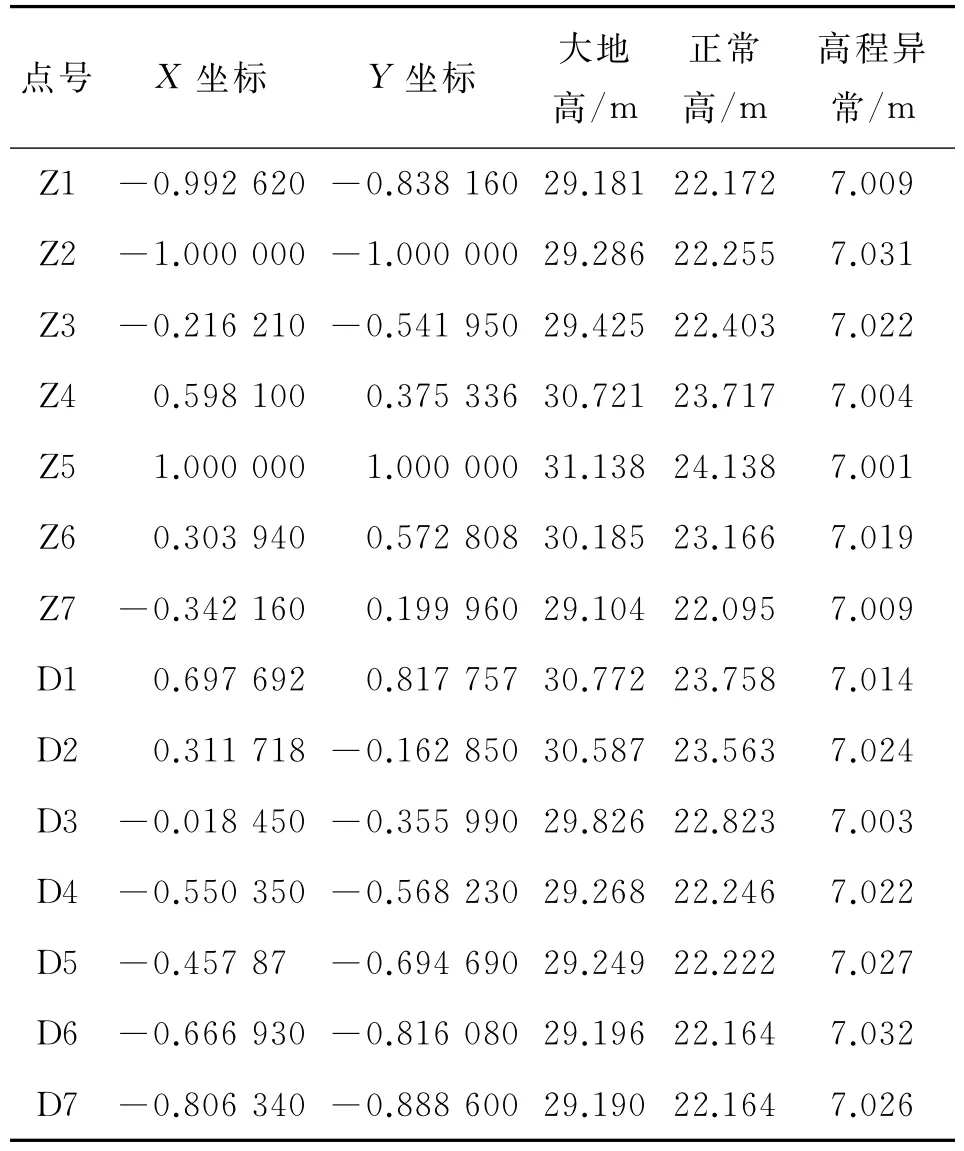
表1 GPS水准点归一化后平面坐标及高程异常数据

（2）LS-SVM的核函数选择和参数优化。采用径向基函数作为LS-SVM的核函数，采用基于交叉核实（cross validate）的格网搜寻法选取最佳参数，从而确定LS-SVM参数。

（3）采用tunelssvm、simlssvm、trainlssvm调用函数对初始化LS-SVM模型进行训练和预测，求得Z1～Z7的残差Δξ（见表2）。

表2 控制点LS-SVM训练残差m

（4）将数据控制点的数据构成文本建立神经网络进行训练。

（5）将待测点的数据构成文本带入训练好的神经网络中，按下式求得高程异常ξ0′及其残差ε（见表3）。

表3 LS-SVM／BP组合模型下GPS水准点高程异常残差m

2.2 拟合精度对比

分别采用平面拟合、二次曲面拟合、LS-SVM模型和BP神经网络进行GPS高程拟合，采用内外符合精度衡量其拟合结果的优劣。各拟合方法的内外符合精度和残差最值见表4，拟合残差见图2。

由表4和图2可以看出：1）LS-SVM的内外符合精度分别为6.63和5.58 mm，其外符合精度优于二次曲面拟合、平面拟合和BP神经网络，说明该方法具有良好的外推能力、较高的泛化能力，能解决小样本、非线性、高维数、局部极小等问题。BP神经网络的内符合精度较高，外符合精度相对较低，但比平面拟合的结果好；二次曲线的拟合结果较好，其拟合精度高于BP神经网络。2）LS-SVM／BP神经网络组合模型的内符合精度介于LS-SVM和BP神经网络两种单一方法之间，但外符合精度比两种单一模型有所提高。外推点（D1～D7）中，BP神经网络的残差变化量相对较大，而组合模型的残差变化量较平稳。表明对于平坦的市政道路，利用LSSVM拟合结果作为神经网络初始权值可克服神经网络等一般机器学习中出现的过学习和局部极值等问题，较好地保持两种模型的各自优点，从而获得较高的拟合精度。

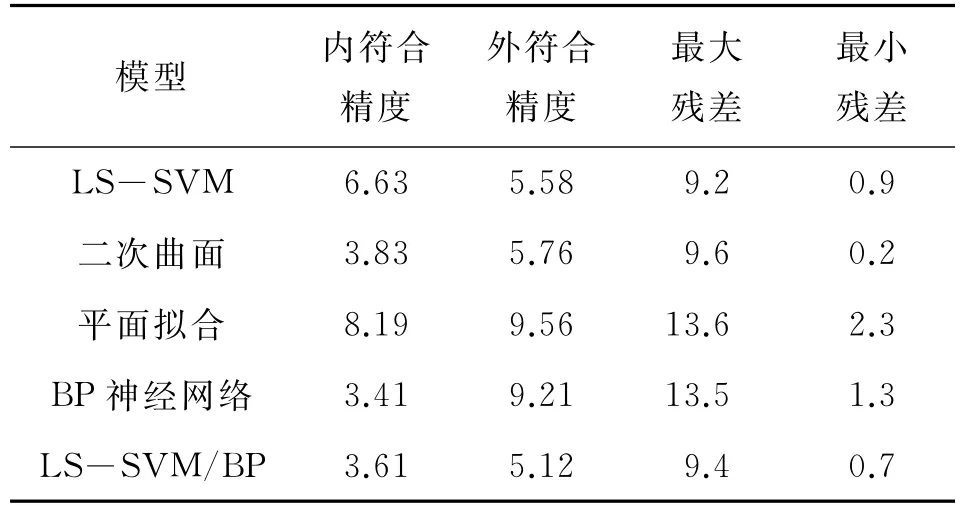
表4 几种模型的拟合精度对比mm

图2 几种模型拟合残差比较

3 结语

将LS-SVM与BP神经网络相结合进行GPS高程拟合，与BP神经网络、二次曲面拟合、平面拟合相比，可提高BP神经网络的外推精度，在GPS高程拟合中具有很大优势。但该方法在支持向量机核函数选择、参数优化方法、神经网络收敛控制参数等方面还有待完善，对于复杂地势的GPS高程控制是否有效也需进一步检验。

［1］ 周忠谟，易杰军，周琪.GPS卫星测量原理与应用［M］.北京：测绘出版社，2002.

［2］ 刘玮，石杏喜.基于多项式的拟合推估法在GPS高程转换中的应用［J］.公路与汽运，2016（2）.

［3］ 顾燕萍，赵文杰，吴占松.最小二乘支持向量机的算法研究［J］.清华大学学报：自然科学版，2010，50（7）.

［4］ 任超，李和旺.最小二乘支持向量机在GPS高程拟合中的应用［J］.工程勘察，2012（7）.

［5］ 陈刚，张明，张芯.基于BP人工神经网络的GPS高程异常拟合方法研究［J］.通信技术，2008，41（11）.

［6］ 高隽.人工神经网络原理及仿真实例［M］.北京：机械工业出版社，2003.

［7］ 沈雪峰，高成发，潘树国.基于最小二乘配置的BP神经网络GPS高程异常拟合方法研究［J］.测绘工程，2010，19（4）.

［8］ 王小辉，王琪洁，丁元兰，等.基于二次曲面和BP神经网络组合模型的GPS高程异常拟合［J］.大地测量与地球动力学，2012，32（6）.

［9］ 闻新，周露，王丹力，等.MATLAB神经网络应用设计［M］.北京：科学出版社，2000.

［10］ 骆思莹，颜怀成，刘伟.基于MATLAB的神经网络法在GPS高程拟合中的应用［A］.江苏省测绘地理信息学会2015年学术年会论文集［C］.2015.

U412.3

A

1671-2668（2016）06-0133-04

2016-08-01