圆的切线证明的常用方法与技巧
胡玉华
(江西省赣州市第一中学)
圆的切线证明的常用方法与技巧
胡玉华
(江西省赣州市第一中学)
圆与生活息息相关,太阳从海平面升起,把海平面看成一条直线包含了圆与直线的三种关系,相交、相切、相离。而切线是当中最特殊的,因为只有一个交点,如地面与自行车轮胎等都是相切的实际情况,圆的切线证明方法很多,就如何证明圆的切线谈谈方法技巧。
圆;切线;垂直;半径
证明一条直线是圆的切线除通过交点个数判断外,通常还有两种情况:(1)未已知切点,用作垂直,证半径的方法。(2)已知切点,连半径,证垂直。下面具体说说这两种方法的应用。
一、利用定义来证明
当题目中未出现直线与圆的交点(即切点未出现)时,我们需要过圆心作直线的垂线段,再利用定义,到圆心的距离等于半径的直线是圆的切线,证明这条直线是圆的切线。
例如:利用角平分线性质证明。
例1.如图1,△ABC中AB=AC,D是BC边的中点,以点D为圆心的圆于AB相切于点E,求证:AC与⊙D相切。
分析:本题中,AC与圆的交点未告知,即不知道切点,所以需要作垂直,通过角平分线性质证明d=r,得出AC是⊙D的切线。
证明:连AD,DE,过D作DF⊥AC
∵AB=AC,BD=CD∴∠BAD=∠CAD
∵AB与圆相切于点E∴DE⊥AB
∵DF⊥AC∴DE=DF∴DF是圆的半径,又DF⊥AC∴AC是圆的切线
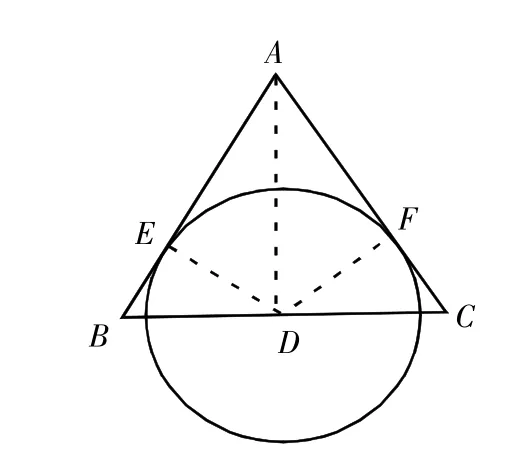
图1
二、运用切线的判定定理证明
1.利用角度转化证垂直
利用角度转化,得到角+角=90°
例2.已知:△ABC内接于⊙O,过点A作直线EF。
(1)如图2,AB为直径,要使EF为⊙O的切线,还需添加的条件是什么(只需写出三种情况)?
(2)如图3,AB是非直径的弦,∠CAE=∠B,求证:EF是⊙O的切线。
分析:第一问是证明切线的最简单情况,已经连接半径,直接证明垂直即可。第二问在第一问的基础上迁移,首先还是要想到连半径证垂直,进而利用同弧所对圆周角相等进行转化,进而证明垂直。

图2
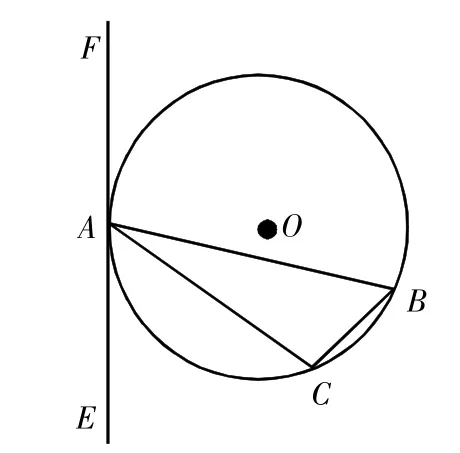
图3
解:(1)①BA⊥EF;②∠CAE=∠B;③∠BAF=90°
(2)连接AO并延长交⊙O于点D,连接CD,
则AD为⊙O的直径,∴∠D+∠DAC=90°
∵∠D与∠B同对弧AC,∴∠D=∠B,又∵∠CAE=∠B,
∴∠D=∠CAE,∴∠DAC+∠EAC=90°
∴EF是⊙O的切线
2.利用全等证垂直
例3.如图4,AB是⊙O的直径,BC⊥AB于B点,连接OC,交⊙O于点E,弦AD//OC,求证:CD是⊙O的切线

图4
分析:要证CD为切线,就要证明∠ODC=90°,即要证明两个三角形全等。
证明:(1)由AD//OC,得∠1=∠2
弧BD所对应圆心角和圆周角:∠BOD=2∠1
而∠BOD=∠2+∠3=∠1+∠3,则∠2=∠3又OB=OD=半径,OC是公共边,所以△COB≌△COD以及BC⊥AB,所以∠ODC=∠OBC=90°
即CD⊥DO于D,即CD是圆O的切线。
总之,几何证明题目千变万化,关键是掌握方法,灵活做出辅助线,合理利用判定定理,掌握好方法技巧,才能以不变应万变,对圆的切线加以判定。
[1]曹文喜.圆的切线的证明[J].考试,2004(12).
[2]王晓峰.巧构圆解题[J].数学月刊,2005(12).
·编辑孙玲娟

