SH波在0.71Pb(Mg1/3Nb2/3)O3-0.29PbTiO3/金刚石界面的反射和透射

孔艳平， 刘金喜， 聂国权

(石家庄铁道大学 工程力学系，石家庄 050043)



SH波在0.71Pb(Mg1/3Nb2/3)O3-0.29PbTiO3/金刚石界面的反射和透射

孔艳平， 刘金喜， 聂国权

(石家庄铁道大学 工程力学系，石家庄 050043)

研究SH波分别从0.71Pb(Mg1/3Nb2/3)O3-0.29PbTiO3(PMN-0.29PT)介质和金刚石介质倾斜入射时在双材料界面上的反射和透射规律。PMN-0.29PT单晶沿[011]c方向极化，宏观上呈正交各向异性性质，且材料主轴沿x3方向旋转切割，数值分析了SH波斜入射时在交界面处的反射、透射系数以及能量反射、透射系数随入射角的变化。结果显示：SH波从金刚石入射时，压电晶体的旋转切割角度对SH波的反射、透射系数和能量分配规律起到非常关键的作用；SH波从压电材料入射时，晶体的旋转切割角度越大，临界角越小，随着入射角的增大，切割角度对SH波反射系数的影响逐渐减小。这些结论可为PMN-PT单晶材料在传感器和频率控制等领域中的应用提供有价值的理论参考。

SH波；PMN-PT单晶；金刚石；反射系数；透射系数

波在弹性介质中反射与透(折)射问题的研究成果被广泛应用于地震勘探、地震工程和非破坏性评估系统中。弹性波在压电材料界面的反射透射问题也涉及到许多工程和工业应用，如传感器、执行器、智能结构和超声波等。在早期，AULD[1]详细研究了弹性波在半无限大压电材料自由表面的反射规律，发现压电晶体对称性、表面电学边界条件以及弹性波入射方向对反射性质均有重要影响。KOSHKINA等[2]以及EVERY等[3]分别研究了弹性波在3 m和2 mm对称压电晶体自由表面的反射问题。弹性波的反射透射理论也可以应用于液体传感器，SHANA等[4]以及NOORBEHESHT等[5]分别研究了平面波在压电陶瓷/流体和压电/水界面的反射和透射规律。YUAN等[6-7]采用电场准静态假设，应用非均匀波理论研究了弹性波在6 mm对称压电晶体半空间表面的反射和在双材料界面的透射问题。SINGH[8]研究了SH波在弹性/压电和压电/压电界面的反射和透射规律，数值分析了反射、透射系数以及能量反射、透射系数随着入射角的变化关系。DARINSKII等[9]研究了弹性波在压电材料界面反射和透射时电磁效应的作用和影响，研究结果表明，尽管电磁波和声波的波速差异较大，但是它们之间存在较强的相互作用。路桂华等[10-11]研究了一维弹性波在压电介质接触界面的反射和透射规律，界面连接方式考虑了分离状态及接触状态两种方式，发现界面分离可以引起高频谐波。BURKOV等[12]研究了有外电场作用时压电介质中体波的反射和透射，并对结果进行了数值模拟。KUANG等[13]以及ZHOU等[14]分析了弹性波在热释电材料和压电材料界面的反射和透射问题，计算了弹性波在半无限大压电介质与真空连接界面之间的二维反射问题。DARINSKII等[15]研究了压电双材料的内部界面对弹性波的影响，推导了界面超声波泄漏引起共振所对应的入射角，建立了共振全反射的条件。ABD等[16-17]研究了在初应力场作用下，QP波和QSV波在两种不同压电介质界面的反射和透射问题，发现初应力的作用不仅使频率发生了偏移，还使表面波波速发生了变化。上述文献选取的压电材料多为压电陶瓷，对于弹性波在新型弛豫型铁电单晶PMN-0.29PT界面的反射和透射问题至今还没有研究，本文以PMN-0.29PT单晶材料为研究对象，当PMN-0.29PT沿不同方向极化时，在宏观上呈现不同对称性质，由于晶体切割方向不同，材料属性不同，弹性波在铁电单晶PMN-0.29PT和弹性介质界面的反射和透射规律将会出现一些新的特点。

1 基本方程的描述及求解

如图1所示，半无限大PMN-0.29PT介质和弹性介质(金刚石)在x2=0界面处完好结合在一起，x3方向垂直于ox1x2的平面，x1轴的一侧为PMN-0.29PT单晶，另一侧为金刚石，在图1中用①和②分别表示两种不同的介质，为了正负号的统一，SH波始终从材料①入射。

图1 SH波在PMN-0.29PT/金刚石界面的反射和透射Fig.1 Reflection and transmission of SH waves at an interface between PMN-0.29PT and diamond

1.1 基本方程

本文研究反平面问题，即只有面外的弹性场与面内的电场耦合，与面内的弹性场无关，也就是u3不为零，面内位移u1=u2=0，而且u3仅与x1和x2有关。PMN-0.29PT单晶沿[011]c方向极化时的本构方程为:

(1)

式中,u3和φ分别为PMN-0.29PT的位移和电势；σ3β和Dβ(β=1,2)分别为应力和电位移；(c44,c45,c55)、(e15,e14,e24)和(κ11,κ12,κ22)分别为PMN-0.29PT晶体在实际坐标系中的弹性常数、压电系数和介电常数。单晶的材料主轴绕x3轴逆时针旋转角度θ，则实际坐标系和晶体坐标系中材料参数的关系可以表示为:

(2)

不考虑体力和自由电荷，应力和电位移满足下面的运动方程:

(3)

式中，ρ为材料密度；t为时间；下标中的逗号表示变量对相应坐标(x1、x2)或时间t的偏微分。

将式(1)代入运动方程(3)，得到控制微分方程:

(4)

对于金刚石介质，其本构关系为:

(5)

金刚石介质的控制微分方程为:

(6)

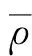
1.2 基本方程求解

假设控制方程(4)解的形式为:

(7)

式中，k为视波数，v为视速度，i为纯虚数，A、B是未知的振幅，q为未知常数。

将式(7)代入式(4)得到:

(8)

式(8)有非零解的条件是其系数行列式的值为零，即:

γ1q4+γ2q3+γ3q2+γ4q+γ5=0

(9)

式中,

γ1=c44κ22+(e24)2,γ2=2(c45κ22+κ12c44+2e24e14),

γ3=c44κ11+4c45κ12+c55κ22+2e15e24+4(e14)2-ρκ22v2,

γ4=2(c45κ11+c55κ12+2e14e15+ρκ12v2),γ5=c55κ11+(e15)2-ρκ11v2

求解式(9)可以得到关于q的四个根，分别代表入(反)射的SH波，入(反)射的声电波(EA波)。PMN-0.29PT压电介质中的总波场可以表示为:

(10)

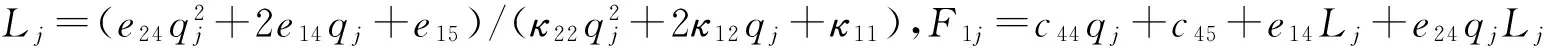
F2j=e24qj+e14-κ12Lj-κ22Ljqj，j=1～4。

同理，解控制方程(6)得到金刚石介质的位移和电势:

(11)

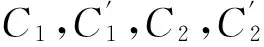
(12)

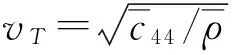
如果SH波从金刚石入射，①代表金刚石，②代表PMN-0.29PT，入射波场为:

(13)

反射波场为:

(14)

透射波场(PMN-0.29PT介质)为:

(15)

如果SH波从PMN-0.29PT介质入射，①代表PMN-0.29PT，②代表金刚石，入射波场为:

(16)

反射波场为:

(17)

透折射波场(金刚石介质)为:

(18)

式中,上标“(I)” 、“(R)”和“(T)”分别为入射波、反射波和透(折)射波。

1.3 反射和透射系数

两个半空间在交界面处是密接的，x2=0处的连续条件为:

(19)

将入射波式(13)或式(16)、反射波式(14)或式(17)和透射波式(15)或式(18)的位移、电势、应力和电位移等代入界面连续性条件式(19)中，可以得到关于反射和透射波幅的4个线性代数方程，写成矩阵形式:

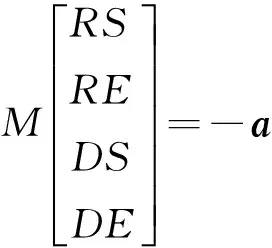
(20)

式中,a为4×1向量；M为4×4矩阵。定义反射和透射系数分别为反射波和透射波波幅与入射波波幅的比值，RS和DS分别代表反射和透射SH波系数，RE和DE分别代表反射和透射EA波系数。当SH波从PMN-0.29PT介质入射时，矩阵M为:

(21)

向量a为:

(22)

因此，通过求解式(20)，可以得到SH波从PMN-0.29PT入射时的反射和透射系数。

当声电EA波从PMN-PT介质入射时，矩阵M与式(21)相同，向量a为:

(23)

类似地，应用同样的方法可以求得SH波从金刚石介质入射时的反射和透射系数。

2 SH波在界面处的能量分配

弹性波在介质中传播时，介质中的各个质点都在自己的平衡位置附近振动，所以它们具有振动动能，同时由于各质点产生了形变，所以还具有弹性势能，弹性波传播的过程同时也是能量传播的过程，一般情况下，用能流密度反应弹性波的传播和强度，我们把垂直于传播方向单位面积上的能量称为能流密度(波印亭矢量)，弹性波在介质中传播时，入射波所携带的能量在遇到界面时会发生改变，能量会重新分配或转换，在电场和磁场的准静态近似下，压电材料的能流密度为:

(24)

式中，Pe(t)为能流密度，是时间t的函数。

弹性材料(金刚石)的能流密度为:

(25)

将式(16)、式(17)和式(18)分别代入式(24)和式(25)中，可以得到PMN-0.29PT中入射波、反射波以及弹性材料中透射波在一个周期内时间平均能流的计算公式。SH波从PMN-0.29PT压电介质入射时，入射SH波的时间平均能流为:

(26)

反射SH波的时间平均能流为:

{P}(Rsh)=-kω(F12-L2F22)(A2)2e2ik(x1+q2x2-vt)

(27)

透射SH波的时间平均能流为:

(28)

反射波强度和透射波强度一般用它们各自所携带的能量占总的入射波能量的比值来反映，用{P}(R)/{P}(Ι)和{P}(T)/{P}(Ι)表示:

(29)

由能量守恒，得到:

(30)

3 数值算例和讨论

前面推导的公式中，PMN-0.29PT沿[011]c方向极化，在宏观上呈现正交各向异性性质，所以上述公式适用于各种正交各向异性压电材料和各向同性弹性材料，表1给出了金刚石和PMN-0.29PT单晶沿[011]c方向极化时的材料常数。

表1 材料特性参数[18-19]Tab.1 Material properties[18-19]

表中,κ0为真空中的介电常数，κ0=8.854×10-12(C2·Nm-2)。

图2 SH波从金刚石入射时x1-x2平面内PMN-PT/金刚石的慢度曲线Fig.2 Slowness curves of PMN-PT/diamond on x1-x2 plane for SH wave incidence from diamond

下面主要讨论SH波在PMN-0.29PT和金刚石交界面处的反射和透射规律，分析反射系数、透射系数、能量反射和透射系数随入射角的变化，以及PMN-0.29PT晶体的切割角度对反射、透射系数、能量反射和透射系数的影响。为了方便讨论，图2给出了SH波从金刚石入射时ox1x2平面内的慢度曲线，坐标系ox1x2与PMN-0.29PT介质的晶体坐标系重合，即旋转角度为0°，临界角可以通过慢度图中的几何关系得到。图3～图10给出了SH波分别从金刚石和PMN-0.29PT单晶入射时的反射和透射系数以及能量反射和透射系数随着入射角的变化，入射角的变化范围为0°～90°。

3.1 SH波从弹性介质入射时在交界面处的反射和透射

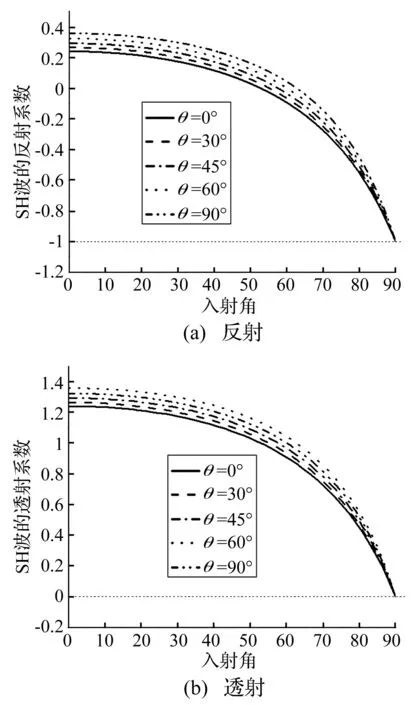
图3 SH波从金刚石入射切割角度不同时 SH波的反射和透射系数随入射角的变化Fig.3 Reflection and transmission coefficients of SH waves varying with the incident angle for different cutting angles for the SH wave incident from diamond medium

由图2可以看出，SH波从金刚石入射时不存在临界角，所以图3～图5所示SH波的反射、透射以及能量反射和透射曲线均为光滑的。图3和图4描述的是SH波从金刚石介质入射时SH波的反射系数和透射系数以及EA波的反射系数随着入射角的变化曲线。由图3可以看出，SH波的反射系数和透射系数均随着入射角的增大而减小，入射角为90°(掠入射) 时，反射系数为-1，透射系数为零，与PMN-0.29PT晶体的切割角度无关，但是当入射角为0° (垂直入射) 时，晶体的切割角度对SH波的反射系数和透射系数影响很大。同时还可以看出，入射角相同的情况下，SH波的反射和透射系数随着晶体切割角度的增大而增大，随着入射角的增大，SH波的反射系数趋于-1，SH波的透射系数趋于零。

图4 SH波从金刚石入射切割角度 不同时EA波的反射系数随入射角的变化Fig.4 Reflection and transmission coefficients of EA waves varying with the incident angle for different cutting angles for the SH wave incident from diamond medium

SH波由弹性介质入射到压电/金刚石界面时，在金刚石界面上有沿界面传播的反射电波(EA波)，由图4(a)可以看出，当入射角为90°时(SH波掠入射)，金刚石介质中EA波的反射系数为零，入射角在0°～90°之间时，EA波的反射系数与PMN-0.29PT晶体的切割角度有关，切割角度越大，EA波的反射系数也越大。PMN-0.29PT透射场中除了SH波以外还有声电波的传播，如图4(b)所示，当SH波垂直入射或掠入射时，EA波的透射系数均为零，其他入射角时，PMN-0.29PT晶体的切割角度对透射场中声电波EA影响很大，电波(EA波)透射系数随入射角的增大先增大后减小，当入射角为65°左右时EA波透射系数达到最大值。相同入射角时，当晶体切割角度为45°时，在PMN-0.29PT透射场中的透射系数大于其它切割角度的透射系数。

下面分析SH波从金刚石入射时能量反射和透射系数随着入射角的变化。反射波和透射波的能量根据式(29)得到。从金刚石入射时，不存在临界角，能量变化曲线光滑连续，如图5所示。入射角在0°～60°，透射SH波携带了绝大部分能量，反射SH波携带的能量较少；入射角超过60°以后，透射SH波携带的能量急剧减小，反射SH波携带的能量急剧增大。PMN-0.29PT晶体0°切割时，入射角为83°时，透射SH波携带的能量与反射SH波携带的能量相等，但是，随着晶体切割角度的增大，透射SH波携带与反射SH波相同能量对应的入射角也随之增大。入射角从0°～60°变化时，透射SH波携带的能量随晶体切割角度的增大而减小，反射SH波携带的能量随晶体切割角度的增大而增大；入射角从60°～90°变化时，透射SH波携带的能量随晶体切割角度的增大而增大，反射SH波携带的能量随晶体切割角度的增大而减小。同时注意到，掠入射(入射角为90°)时，透射SH波携带的能量为0，反射SH波携带了全部的能量。由以上分析可以看出，晶体切割角度对SH波透射和反射的能量分配起到非常关键的作用，而且，透射SH波和反射SH波的能量系数之和为1，充分证明前面公式推导是正确的。

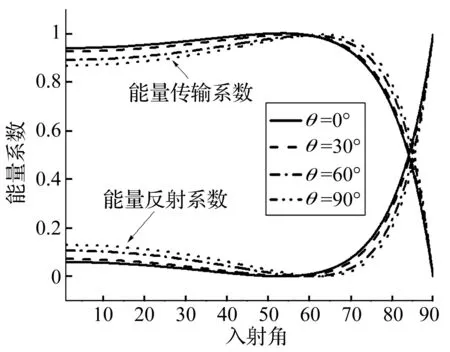
图5 SH波从金刚石入射切割角度不同时能量随入射角的变化Fig.5 Energy coefficients varying with the incident angle for different cut angles of the SH wave incident from diamond medium

3.2 SH波从PMN-0.29PT介质入射时在交界面处的反射和透射

由慢度曲线图2可以看出，SH波从PMN-0.29PT入射时存在一个临界角，临界角为15.112°，由图6～图10可以看出，反射和透射曲线不连续，有一个尖点，此处的入射角为SH波发生全反射时对应的临界角，并且临界角的大小与PMN-0.29PT压电晶体的切割角度密切相关。图6描述的是SH波的反射系数随着入射角的变化曲线，可以看出，当入射角较小(小于临界角)时，SH波的反射系数随入射角的增大而增大；当入射角大于临界角以后，SH波的反射系数随入射角的增大而减小。临界角的大小与PMN-0.29PT压电晶体的切割角度有关，切割角度越大，临界角越小，同时SH波的反射系数也越小，但是，随着入射角的增大，晶体的切割角度对SH波反射系数的影响越来越小，当入射角大于60°时，可以忽略晶体切割角度对SH波反射系数的影响，反射系数接近-1。图7是EA波的反射系数随入射角的变化，可以看出，当入射角小于临界角时，EA波的反射系数几乎为零，晶体切割角度对EA波反射系数的影响可以略去不计，当入射角较大时，晶体的切割角度对EA波反射系数产生了较大的影响，切割角度θ=0°和θ=90°时EA波的反射系数较小。

图6 SH波从PMN-0.29PT入射切割角度 不同时SH波的反射系数随入射角的变化Fig.6 Reflection coefficients of SH waves varying with the incident angle for different cutting angles for the SH wave incident from PMN-0.29PT

图7 SH波从PMN-0.29PT入射切割角度 不同时EA波的反射系数随入射角的变化Fig.7 Reflection coefficients of EA waves varying with the incident angle for different cutting angles for the SH wave incident from PMN-0.29PT

图8和图9描述的是金刚石透射波场中SH波和EA波的透射系数随入射角的变化，可以看出，SH波的反射和透射系数变化规律相似，但是透射的SH波系数都大于零，当入射角大于60°时，可以忽略晶体切割角度对SH波反射系数的影响，透射系数接近零。图9是EA波的透射系数随入射角的变化，可以看出，当入射角小于临界角时，透射EA波系数几乎为零，当入射角较大时，晶体的切割角度不同，对EA波透射系数也不同，随着入射角的增大，PMN-0.29PT压电晶体切割角度为θ=0°和θ=90°时EA波透射系数趋于零。

图8 SH波从PMN-0.29PT入射切割角度 不同时SH波的透射系数随入射角的变化Fig.8 Transmission coefficients of SH waves varying with the incident angle for different cutting angles for the SH wave incident from PMN-0.29PT

图9 SH波从PMN-0.29PT入射切割角度 不同时EA波的透射系数随入射角的变化Fig.9 Transmission coefficients of EA waves varying with the incident angle for different cutting angles for the SH wave incident from PMN-0.29PT

图10给出了SH波从PMN-0.29PT单晶材料入射时反射和透射波所携带的能量随入射角的变化。在到达临界角之前，透射SH波携带了绝大部分能量，其能量随着入射角的增大而增大；反射SH波仅携带一小部分能量，其能量随着入射角的增大而减小。由图10还可以看出，反射波和透射波所携带的能量与PMN-0.29PT单晶的切割角度有关，反射SH波的强度随着晶体切割角度的增大而增大，而透射SH波的强度随着晶体切割角度的增大而减小,当入射角超过临界角以后，SH波在界面处发生全反射现象，反射的SH波的能量为1，透射的SH波的能量为零。

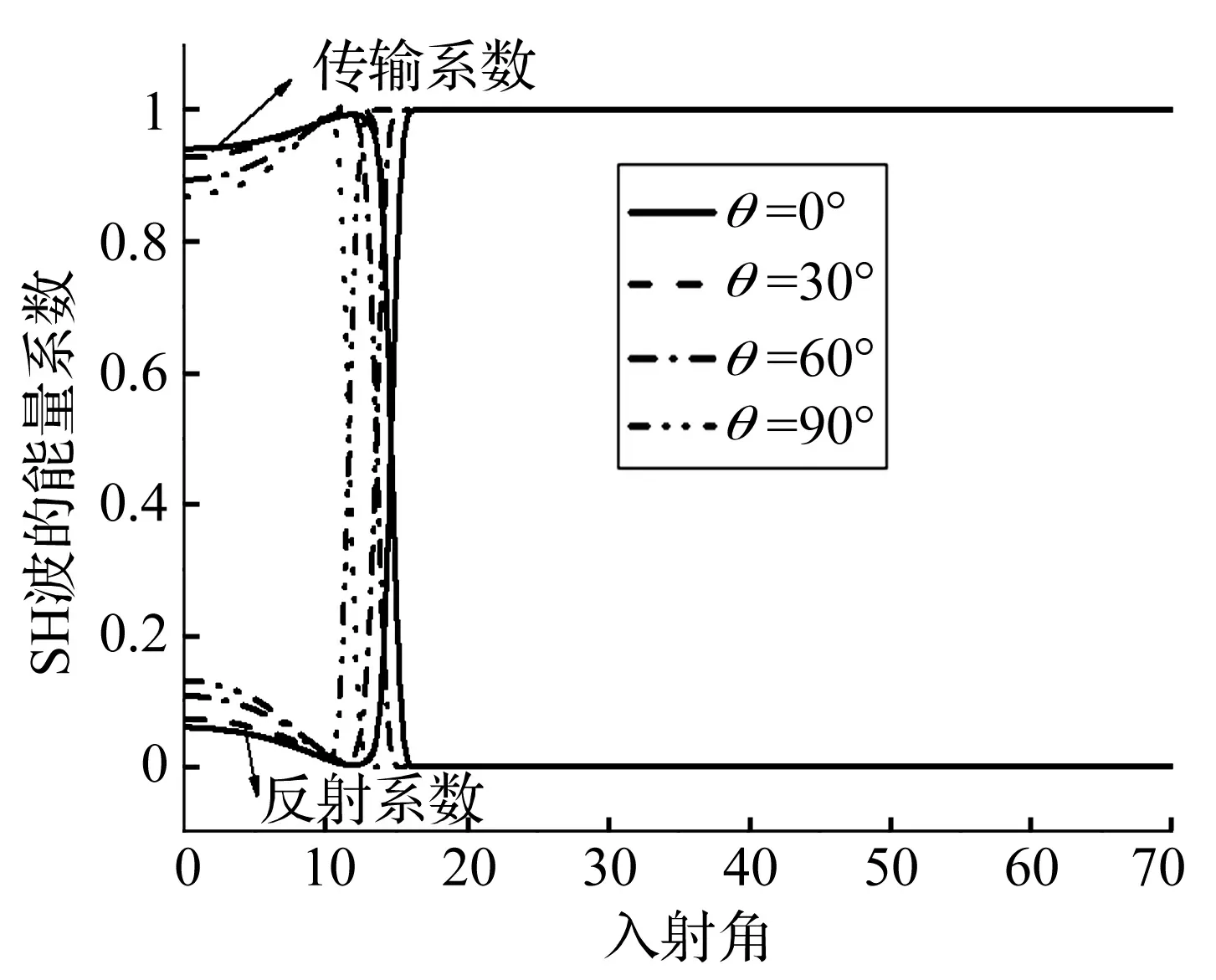
图10 SH波从PMN-0.29PT入射切割角度 不同时能量随入射角的变化Fig.10 Energy coefficients varying with the incident angle for different cutting angles of the SH wave incident from PMN-0.29PT medium

4 结 论

本文通过研究SH波在PMN-0.29PT晶体和弹性材料(金刚石)界面上反射和透射性质，详细讨论了PMN-0.29PT的切割角度对反射、透射系数以及能量分配规律的影响。研究结果表明：

(1) SH波从金刚石入射时，透射的SH波携带了绝大部分能量，反射的SH波携带的能量较小，随着晶体切割角度的增大，透射SH波与反射SH波携带相同能量对应的入射角也增大。晶体切割角度对SH波透射和反射的能量分配起到非常关键的作用。

(2) SH波从PMN-0.29PT入射时，当入射角小于临界角时，SH波的反射系数随入射角的增大而增大，当入射角大于临界角时，SH波的反射系数随入射角的增大而减小，并且PMN-0.29PT晶体的切割角度越大，临界角越小，同时SH波的反射系数也越小，但是，随着入射角的增大，晶体切割角度对SH波反射系数的影响越来越小。

[1] AULD B A. Acoustic fields and waves in solids[M]. Florida: Kreiger Publishing Company, 1990.

[2] KOSHKINA E N, LYAMOV V E, MAMATOVA T A. Reflection of acoustic waves in the case of conical refraction[J]. Soviet Physics Crystallography, 1978, 23: 721-722.

[3] EVERY A G, NEIMAN V I. Reflection of electroacoustic waves in piezoelectric solids: mode conversion into four bulk waves[J]. Journal of Applied Physics, 1992, 71(12): 6018-6024.

[4] SHANA Z, JOSSE F. Reflection of bulk waves at a piezoelectric crystal-viscous conductive liquid interface[J]. The Journal of the Acoustical Society of America, 1992, 91(2): 854-860.

[5] NOORBEHESHT B, WADE G. Reflection and transmission of plane elastic-waves at the boundary between piezoelectric materials and water[J]. The Journal of the Acoustical Society of America, 1980, 67(6):1947-1953.

[6] YUAN X, ZHU Z H. Wave reflection in piezoelectric half-plane[J]. International Journal of Applied Mechanics, 2013, 5(2):238-249.

[7] YUAN X, ZHU Z H. Reflection and refraction of plane waves at interface between two piezoelectric media[J]. Acta Mechanica, 2012, 223(12): 2509-2521.

[8] SINGH B. Propagation of shear waves in a piezoelectric medium[J]. Mechanics of Advanced Materials and Structures, 2013, 20(6): 434-440.

[9] DARINSKII A N,CLEZIO E L, FEUILLARD G. The role of electromagnetic waves in the reflection of acoustic waves in piezoelectric crystals[J]. Wave Motion, 2008, 45(4): 428-444.

[10] 路桂华, 于桂兰, 汪越胜. 弹性波透过压电介质接触界面的传播特性[J]. 科学技术与工程, 2005, 5(3): 174-175. LU Guihua, YU Guilan, WANG Yuesheng. Behavior of elastic waves propagating through a contact interface between two piezoelectric solids[J]. Science Techonlogy and Engineering, 2005,5(3): 174-175.

[11] 路桂华, 汪越胜, 于桂兰. 弹性波在压电介质摩擦接触界面上的反射与透射[J]. 应用基础与工程科学学报, 2006, 14(1): 77-83. LU Guihua, WANG Yuesheng, YU Guilan. Reflection and transmission of elastic waves at a friction contact interface between two piezoelectric media[J]. Journal of Basic Science and Engineering, 2006, 14(1): 77-83.

[12] BURKOV S I, SOROKIN B P, GLUSHKOV D A, et al. Theory and computer simulation of the reflection and refraction of bulk acoustic waves in piezoelectrics under the action of an external electric field[J]. Crystallography Reports, 2005, 50(6): 986-993.

[13] KUANG Z B, YUAN X G. Reflection and transmission of waves in pyroelectric and piezoelectric materials[J]. Journal of Sound and Vibration, 2011, 330(6): 1111-1120.

[14] ZHOU Z D, YANG F P, KUANG Z B. Reflection and transmission of plane waves at the interface of pyroelectric bi-materials[J]. Journal of Sound and Vibration, 2012, 331(15): 3558-3566.

[15] DARINSKII A N, WEIHNACHT M. Resonance reflection of acoustic waves in piezoelectric bi-crystalline structures[J]. Ultrasonics, Ferroelectrics and Frequency Control, IEEE Transactions on, 2005, 52(5): 904-910.

[16] ABD-ALLA A N, ALSHEIKH F A. Reflection and refraction of plane quasi-longitudinal waves at an interface of two piezoelectric media under initial stresses[J]. Archive of Applied Mechanics, 2009, 79(9): 843-857.

[17] ABD-ALLA A N, ALSHEIKH F A, Al-HOSSAIN A Y. The reflection phenomena of quasi-vertical transverse waves in piezoelectric medium under initial stresses[J]. Meccanica, 2012, 47(3): 731-744.

[18] CHEN C W, ZHANG R, CAO W W. Theoretical study on guided wave propagation in (1-x)Pb(Mg1/3Nb2/3)O3-xPbTiO3(x=0.29 and 0.33) single crystal plates[J]. Journal of Physics D-Applied Physics, 2009, 42: 095411.

[19] BENETTI M, CANNATD,PIETRANTONIO F D, et al. Gigahertz-range electro-acoustic devices based on pseudo-surface-acoustic waves in AlN/diamond/Si structures[J]. Applied Physics Letters, 2005, 87(3): 033504.

Reflection and transmission of SH waves at interface between 0.71Pb(Mg1/3Nb2/3)O3-0.29PbTiO3and diamond

KONG Yanping, LIU Jinxi, NIE Guoquan

(Department of Engineering Mechanics, Shijiazhuang Tiedao University, Shijiazhuang 050043, China)

The reflection and transmission of SH waves at the interface between 0.71Pb(Mg1/3Nb2/3)O3-0.29PbTiO3(PMN-0.29PT) and diamond were discussed. The PMN-0.29PT single crystal under consideration was polarized along the [011]cdirection to get a macroscopic symmetry of orthonormal 2 mm and the cut orientation on the material was made to have an angle with the XZ-plane. The reflection and transmission coefficients and energy distribution coefficients varying with the incident angle were analyzed under the oblique incidence of SH waves. The results show that the cut orientation is critical for the reflection and transmission coefficients and energy distribution coefficients when SH waves are incident from diamond media. When SH waves are incident from piezoelectric media, the larger the cut angle, the smaller the corresponding critical angle, and the cut angle has little influence on the reflection and transmission coefficients for a given large incident angle. The results are valid for the signal processing, transduction, and frequency control of PMN-PT single crystal composite devices.

SH wave; PMN-PT single crystal; diamond; reflection coefficients; transmission coefficients

国家自然科学基金(11272221);河北省自然科学基金 (A2015210092)资助项目

2015-06-17 修改稿收到日期：2015-11-11

孔艳平 女，副教授，博士，1977年生 E-mail:lkongyanping1977@163.com

O346

A

10.13465/j.cnki.jvs.2016.22.028