基于数值试验的波浪载荷激励船舶振动响应研究

唐宇航， 陈志坚， 张佳栋

(海军工程大学 舰船工程系，武汉 430033)



基于数值试验的波浪载荷激励船舶振动响应研究

唐宇航， 陈志坚， 张佳栋

(海军工程大学 舰船工程系，武汉 430033)

即使未发生砰击振动和显著非线性波激振动，船体由较低频波浪诱导产生的振动响应中依然存在高频振动分量且高频振动衰减缓慢。从单自由度系统简谐激励振动理论入手，指出响应解析解中常被忽略的伴随自由振动项是导致高频振动的一个因素，在系统阻尼较小、自振频率较低时瞬态响应成分短时间内难以衰减，推导了位移、速度、加速度和内力响应中高频成分的占比规律。分析了波浪载荷作用于船体时 “时变、场变” 的性质，及船舶小阻尼系统的特点，认为伴随自由振动在波浪载荷激励振动响应预报领域中有重要地位，对比时域法和频域法在理论基础上的差异，发现了时域法在处理该问题时的优越性。通过对双体船进行数值仿真，结合海浪资料对该船16个航行工况的振动响应进行预报，结果表明各振动响应中均存在稳态高频分量且占比较高，得出了高频分量与频率比关系的规律性结论，为时域中波激振动的进一步研究提供了思路。

伴随自由振动；动力响应；高频振动；时域法；非线性；波激振动

如今，关于船舶在波浪载荷作用下的振动描述主要包括砰击振动和波激振动。砰击振动是船舶在瞬时波浪冲击载荷下引起的颤振，是以船舶固有频率衰减的自由振动现象，持续时间不长；波激振动则是波浪激励下引起的船体谐和振动现象，持续时间较长。根据北大西洋和西北太平洋的海浪统计资料，常见波浪周期一般不低于3.5 s，即使再考虑船-波的相对运动，那么波浪载荷所对应的遭遇频率一般也不会高于船体一阶总振动频率。波激振动有线性(船体梁一阶总振动频率等于或接近遭遇频率)和非线性(船体梁一阶总振动频率等于遭遇频率的整数倍n)之分[1]。因此，由低频波浪载荷所激起的船体高频振动(以遭遇频率为基准)，往往仅认为是由砰击振动[2]或其与非线性波激振动的组合导致的。

用于评价船体振动响应水平的振动衡准特征参数一般是位移、速度、加速度和应力[3]。有资料表明，在实船测试、波浪载荷作用下的模型试验中均发现，在各种不同波浪载荷条件下，均存在船体高频振动响应比较剧烈的现象，产生严重的疲劳问题[4]。结合波浪载荷工况，对这类响应参数的时域信号进行幅频响应分析时发现一种情况，即使船舶首阶固有频率远远大于波浪遭遇频率，往往在近十倍以上，仍然存在比较显著的高频振动分量(以加速度响应最为明显)，幅频曲线中的响应峰值位置对应船体一阶、甚至多阶固有频率，然而在该工况下的实船测试和模型试验中却均未发现船体砰击现象。直觉上可以认为产生了非线性波激振动，但这种认识与非线性波激振动的当前定义不一致，即n为整数倍且该整数较小时非线性波浪荷载中某阶倍频成分才容易激起船体共振[5]，此外，非线性波激振动往往只是指船体的一阶共振。可见，船体在波浪载荷作用下高频振动响应问题需要进一步研究。

为解释低频波浪荷载作用时船体存在高频振动响应成分的原因，探究不同振动衡准特征参数响应对波浪载荷相对频率(相对于船体固有频率)的敏感程度，分析不同波浪遭遇频率下，船体高频振动响应在总振动响应中的占比规律。本文从结构动力学基本理论入手，发现伴随自由振动是引起高频振动的一个重要因素，人们一般认为该振动会随时间延长而衰减，常常很少关心它，但对于“既时变又场变”的波浪载荷，这种瞬态响应在理论预报和工程实践中的作用却有重要地位，从而为低频波浪下船体存在稳态高频振动找到了理论依据。同时结合目前该领域的研究方法，即频域法和时域法，分析出时域法在处理非线性问题中的优势，文中以双体船为背景进行仿真计算并结合其航行、振动特点，将时域法应用在数值试验中，对所得响应数据进行处理，从而得到了一些有意义的结论。

1 单自由度系统简谐激励振动理论

1.1 运动微分方程

波浪载荷对船体的激励在一个较短的时间内，可认为是简谐变化的，船体产生特定的振动(两节点总振动)可认为是单自由度的，因此使用简谐激励作用下单自由度系统响应理论进行研究是合适的。

单自由度系统在简谐激励下的振动方程[6]：

(1)

式中，M为体系的质量；K为体系的刚度；C为体系的阻尼系数；P(t)为简谐干扰力；P0为激励力幅值；ω为激励力频率；β为激励力的相位角。

对于黏性小阻尼系统，上述方程的通解形式为:

(A1cos(ωt+β)+A2sin(ωt+β))

(2)

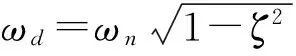
1.2 伴随自由振动项与强迫振动项的幅值对比

伴随自由振动响应的衰减项决定衰减速率，非衰减项决定初始振幅的大小。RX、RV、RA和RF分别表示位移、速度、加速度和内力的伴随自由振动振幅与强迫振动振幅之比[7]，ηX、ηV、ηA和ηF分别表示位移、速度、加速度和内力的伴随自由振动振幅与总振幅之比。由于船舶是小阻尼系统，模态阻尼一般不超过5%，所以在推导中会用到ζ≪1且ζ2≈0的条件，RX、RV、RA和RF的简要推导如下：

(3)

(4)

则：

(5)

(6)

则：

(7)

[mω2A1cos(ωt+β)+(P0-mω2A2)sin(ωt+β)]-

(8)

则：

(9)

1.3 伴随自由振动占比的讨论

结合已有研究并考虑避免砰击，重点对5、6级海况中特定波浪所诱导的波浪激励进行计算，依据GWS的北大西洋 8、9、15及16四海区的海浪长期统计资料NA-1C，查表估算得到最大概率波浪周期[8]，从而决定波浪的基频范围，同时考虑船-波相对运动的多普勒效应，并以船舶模态阻尼系数中低阻尼曲线为参考，相关参数范围选取见表1。

表1 波浪参数及相关参数可行范围Tab.1 Wave parameters and practicable scope of relevant parameters

表2 计算公式汇总Tab.2 Summary of formulas

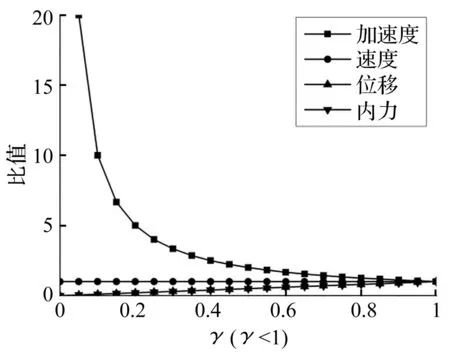
图和随γ(γ<1)的变化规律Fig.

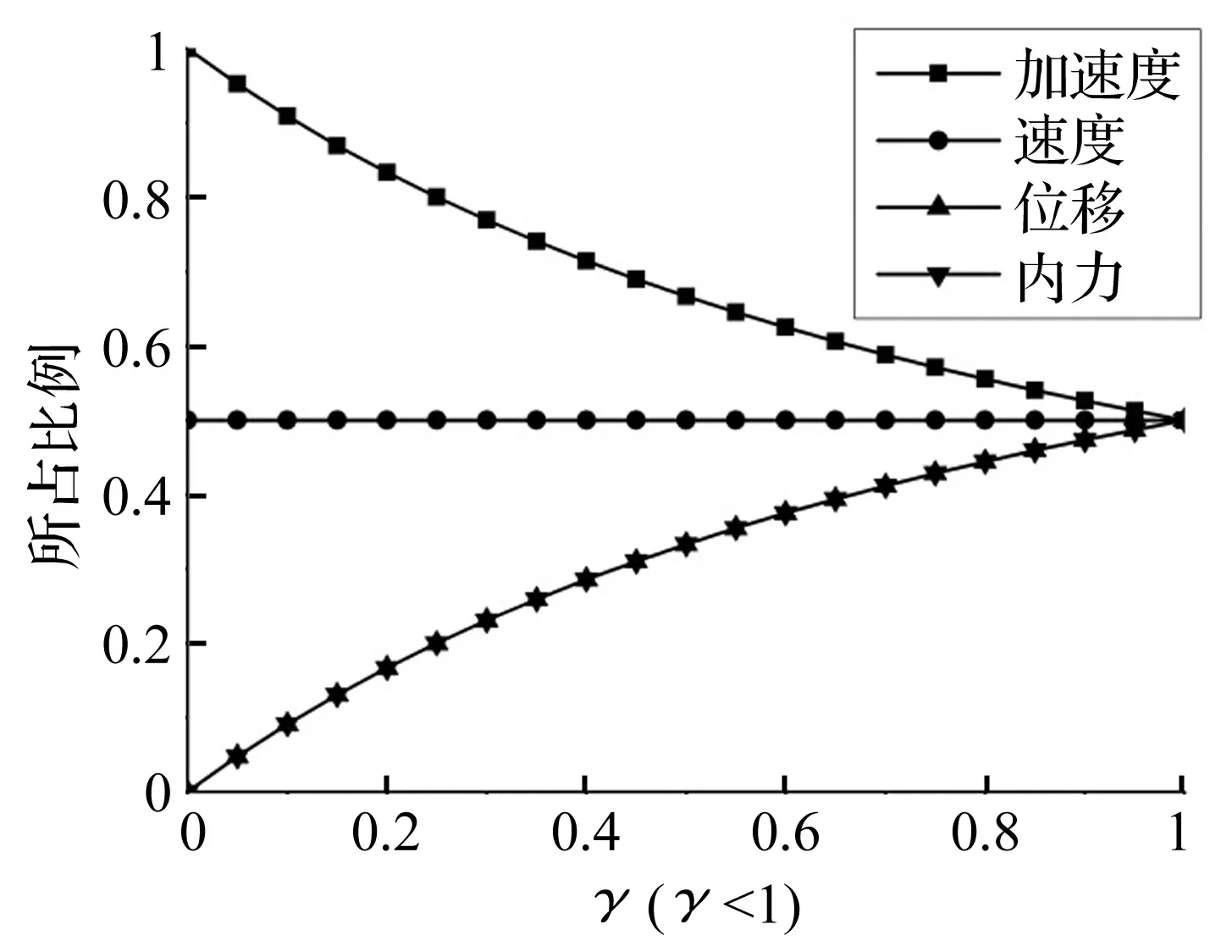
图和随γ(γ<1)的变化规律Fig.

γ<1时，加速度响应中伴随自由振动成分在短时间内一直较大，选择对加速度响应衰减进行时间历程分析。依据表1参数，相同荷载频率、不同阻尼比、不同自振频率下的ηA随时间(覆盖多个波浪周期，取40 s)的变化历程在图3中给出。可以看出，阻尼越大衰减速度越快；在频率比γ<1范围内，即使存在阻尼的作用，伴随自由振动成分也没有衰减到可以忽略的地步，甚至可以认为伴随自由振动在一定时间范围内起主导作用。

以上的讨论是基于单自由度体系下的理论推导，不能完全一致地适用于多自由度体系的响应预报，但是其规律性方面值得参考，可以推广至多自由度体系的研究中。

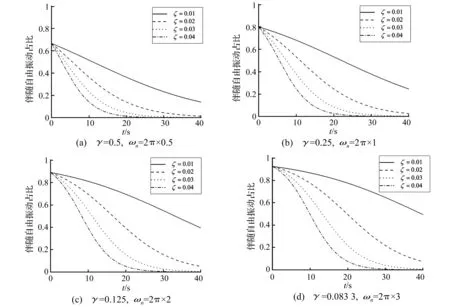
图3 伴随自由振动在加速度总响应中占比ηA随时间的衰减曲线 (每个图中4条曲线从上到下分别对应于ζ=0.01、0.02、0.03、0.04)Fig.3 Attenuation curve of acceleration response in the proportion of the total response (ηA) with time

2 理论预报研究方法

目前关于波浪激励下船体振动响应研究，主要采用三维水弹性理论进行预报，但大多数是在频域上进行[9]，该方法常在线性理论极值和非线性特性不显著的疲劳损伤预报时采用，计算相对简单快捷；而时域法可考虑波浪载荷及系统几何非线性，更适合处理瞬态问题、时历响应及船体大幅运动的非线性问题，分析精度高[10]，但其在波浪载荷预报领域的发展和应用还不够成熟[11]。以下对频域法和时域法的差异进行理论分析。

对多自由度体系进行动力反应分析时常使用模态叠加法，以实现向单自由度体系运算的转化，该方法既可以在时域上进行，也可以在频域上进行，但是各自的理论基础和适用范围均有差异。以位移叠加法为例，振型叠加法(模态叠加法)将各阶振型位移的贡献叠加起来，即：

x(t)=φ1Y1(t)+φ2Y2(t)+…+φNYN(t)

(10)

式中,Yn(t)为每一阶振型的总反应。

(1)在时域中，每一阶振型总反应可由Duhamel积分表示，即：

(11)

其中，

(0<ζn<1)

(12)

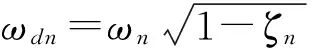
hn(t-τ)可以由单自由度体系下的阻尼单位脉冲反应函数类比获得。对于低临界阻尼体系，除了由微分冲量所引起的自由振动反应按指数衰减外，黏滞阻尼体系在一般动力荷载下反应推导与无阻尼情况完全相同。无阻尼体系中，对于任意一般荷载p(t)，在t=τ时作用的载荷强度为p(τ)，短时间dτ内载荷在结构上产生的冲量为p(τ)dτ，该冲击荷载造成的反应近似分析如下。

短时冲击荷载作用下，结构在很短时间内达到最大反应，此期间阻尼力来不及从结构中吸收太多能量，因此只需讨论冲击载荷下体系的无阻尼反应。对于质量m的冲量-动量关系可以写成：

(13)

(14)

加载结束后反应为自由振动：

(15)

(16)

从时域法的推导过程中可以发现，该方法是对短时间冲量p(τ)dτ进行反应计算，反应是以瞬态自由振动为解，在时域上进行积分，充分考虑了dτ时间内系统的自由振动效应。Msc.nastran中瞬态响应计算正是对应于时域法，通过数值计算将连续积分离散化，计算多个时间步长下的累积响应，可以将伴随自由振动考虑在内。

(2)在频域中，每一阶振型总反应:

(17)

式中，Pn(iω)为复荷载函数，是Pn(t)的Fourier变换。复荷载函数Pn(iω)和复频反应函数Hn(iω)如下表达：

(18)

(ζn>0)

(19)

叠加法中多自由度系统的复频反应函数与单自由度类似，由以下推导求出。

使用指数形式对稳态谐振反应求解，描述谐振荷载一般情况为:

(20)

本研究取相位角β=0，方程的特解为：

x(t)=Geiωt

(21)

解出常复数G为：

(22)

复频反应函数H(iω)就是由G除以载荷幅值以后给出。

分析中发现，频域法在求解运动微分方程时，忽略了简谐荷载作用下式(20)的通解，即伴随自由振动项，它仅考虑了特解，即强迫振动项。频域法是一种针对固定幅值、固定位置的谐振响应计算方法，频率响应分析用于计算结构在简谐载荷作用下对每一个计算频率的动响应；而时域法则将有初始条件的自由振动和伴随自由振动考虑在内，瞬态响应分析可以用于计算时变、场变激励载荷作用下结构的动力行为，方便地处理非线性运动问题。

一般情况下，认为自由振动部分会随时间的延长而趋于衰减，常常很少关心它，但这一般是针对系统阻尼和自振频率较高、初始条件恒定的问题而言[12]。但对受波浪作用的船体，在载荷作用的每个变化周期内，波浪在船体水线附近的作用位置(湿表面)是变化的，即力的作用点是“场变的”，此外，这部分船体湿表面所受的波浪力是随时间变化的、是非连续的，即力的大小和方向是“时变的”。因此，对于波浪中航行的船舶而言，波浪激励力既是“时变的”、同时亦是“场变的”，每一时刻都存在一个新的初始条件，对应每一时刻的初始条件，将产生一个新的伴随自由振动，由于船舶是一个小阻尼系统，瞬态反应不易于衰减，是多个伴随自由振动相叠加。那么在相当长一段时间中，伴随自由振动项大小起主要作用，所以在有必要通过时域法探究伴随自由振动对总振动的影响，以及低频波浪载荷与船舶高频振动响应的关系，从而进一步认识高频振动响应的重要性。

3 数值仿真试验

3.1 有限元计算模型

双体船具有与常规单体船不同的结构形式，振型多样也更为复杂[13]，总振动频率较为密集，因此研究波浪载荷引起的高频振动对双体船而言意义更为重要。双体船模型相关尺度见表3，依据模型资料按照《小水线面双体船指南》要求构造全船有限元模型，各层甲板、舱壁板和舷侧板等都采用板单元来模拟，横梁、纵桁和肋骨等采用梁单元模拟，有限元模型的网格尺度按一个纵骨或一个肋位间距的小者划分[14]。为确保准确地模拟船体结构，精确地计算船体整体和局部瞬态响应，所有对船体强度及振动有影响的因素都加以考虑。全船有限元模型如图3所示，共有95 760个节点，212 518个单元。

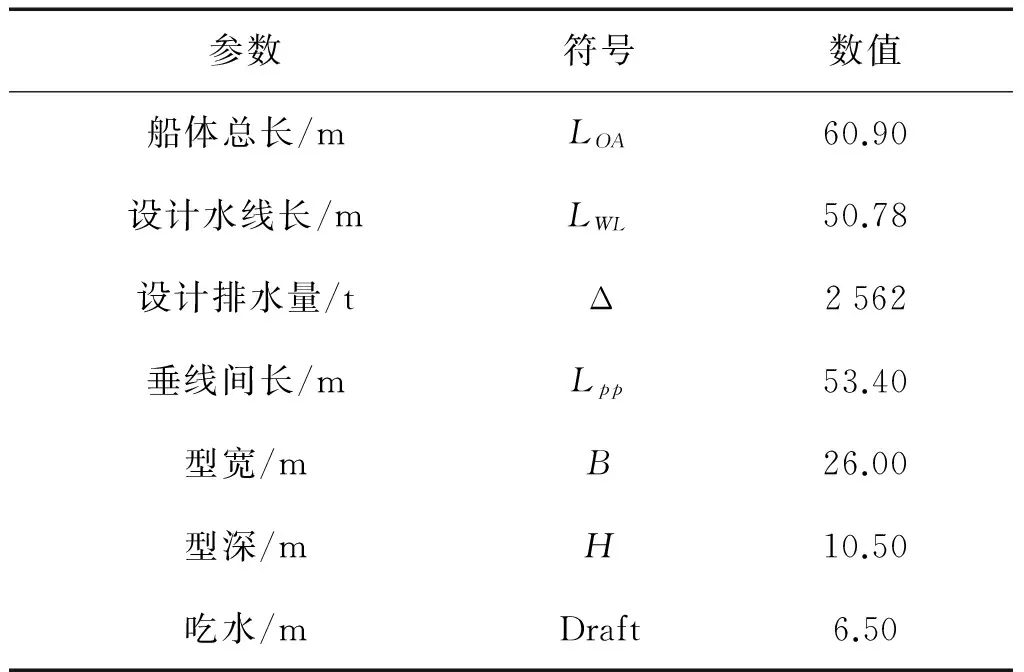
表3 计算模型的参数Tab.3 Parameters of calculate model

图4 有限元整船模型Fig.4 Whole ship finite element model

3.2 计算波浪载荷和试验工况设计

波动压力以面压力的方式直接作用在整船有限元模型的湿表面上，将波浪载荷函数转换成Nastran中用PCL语言描述的Field场函数进行加载，同时采用虚质量法考虑流固耦合效应，即实现了整船有限元模型计算的工况构建[15]。仅考虑单项或线性波浪激励，船舶的高频响应可能会被严重低估[16-17]，因此本文采用基于有限幅波理论的波面函数的3阶显式表达式[18]：

(23)

设双体船表面在有限幅波中航行时所受到的脉动压力为p(x,y,t)，根据伯努利方程得：

pS(x,y,z,t)+pR(x,y,z,t)+pW(x,y,z,t)+

pD(x,y,z,t)

(24)

式中，a为波幅；k为波数；ΦW为入射波势；ΦR为辐射波势；ΦD为绕射波势；ps(x,y,z,t)为船体运动而引起的流体静水压力的变化，pR(x,y,z,t)为船体运动而引起的辐射压力；pW(x,y,z,t)为入射波引起的波浪压力，即波浪主干扰力；pD(x,y,z,t)为因船体对入射波的限制而引起的绕射压力。

在1.3节中提到，本文按实际海浪观测资料决定波浪激励力的基频和波高参数，重点对5级、6级海况进行分析，波高由各级海况波高的上下限均值来决定，分别为3.25 m和5m。NA-1C海浪长期统计资料的有义波高为三参数的Weibull分布、跨零波浪周期为log-normal分布。其有义波高的Weibull分布为：

(25)

式中，H1=3.041，j=1.484，H0=0.66。跨零波浪周期的log-normal分布为：

(26)

计算波浪取最大概率波浪，即在本级海况有义波高条件下，波浪周期有最大发生概率p(tz/hs)的规则波，p(tz/hs)按式(26)进行计算，这是在平稳海况中最易遭到的波浪，表4中列出了5级、6级海情下波浪参数和概率。表5中给出了16个计算工况，其中包括5级海情下0 kN、6 kN和12 kN航速，180° 、135°、90°和0°浪向角的12个组合工况，6级海情下12 kN航速，180° 、135°、90°和0°浪向角的4个组合工况。

表4 波浪参数及发生概率计算表Tab.4 Wave parameters and occurrence probability calculation table

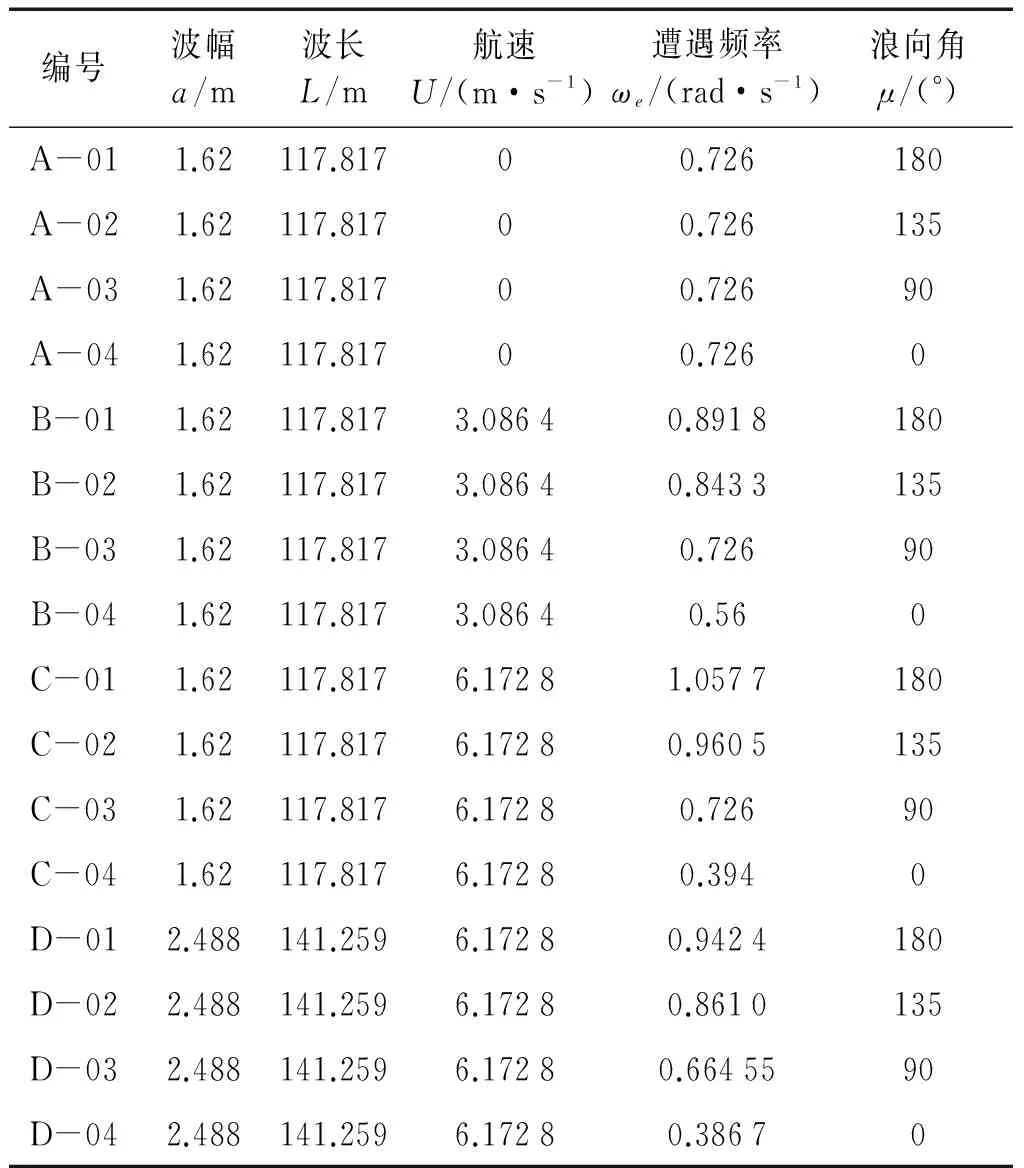
表5 数值仿真试验计算工况Tab.5 Calculation conditions of numerical simulation experiment

3.3 仿真试验结果分析

应用Msc.Nastran对整船有限元模型进行模态分析，得出干模态固有频域和湿模态固有频率，其中计算湿模态时通过虚拟质量法考虑船体湿表面与静水的耦合作用，计算结果见表6。采用瞬态响应分析对船体动响应进行预报，参考《水面舰艇振动评价基准》中关于评价区域的要求，选取1甲板艉端左舷边位置(node 32 346)分析，计算总时长42 s。

图5为D-03工况下1甲板艉端左舷边(node 32 346)位移响应合成、高频和低频时间历程曲线，其中存在重要的高频分量。黑色为合成成分，蓝色为高阶成分，红色为波频成分。D-03工况下1～3倍遭遇波频分别为0.105 8 Hz(即0.664 55 rad/s)、0.211 6 Hz和0.317 5 Hz，对node 32 346的位移响应时域信号进行低通滤波，得到0.4 Hz以下的波频信号成分，为稳定的有限幅波3阶波频合成成分。该船总振动首阶频率为2.576 3 Hz，再对node 32 346的位移响应时域信号进行高通滤波，得到2 Hz以上的高频信号成分，包含了该船总振动频率下高阶成分。图6为D-03工况下node 32 346的位移响应频谱分析图，图中低频波浪荷载导致的0.4 Hz以下的低频分量，同伴随自由振动导致的按固有频率振动的高频分量在量值上相当。从图5中可以看出在计算的40 s内高频分量没有显著的衰减，而此时的1～3倍波浪遭遇频率和该船首阶总振动频率之比分别为γ=0.041、0.082和0.123，说明在船舶首阶固有频率远大于波浪遭遇频率(近十倍以上时)、不会发生非线性波激振动的情况下，仍存在高频振动响应比较显著的现象，换句话说即使有阻尼的存在，其伴随自由振动响应导致的高阶振动也难以在短时间衰减，从而不能被测试和分析所忽略。

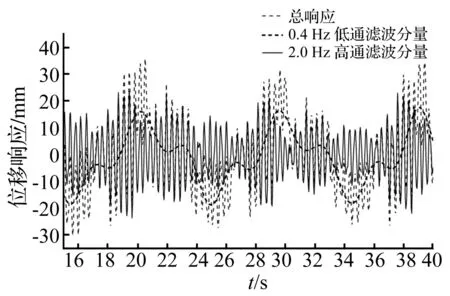
图5 D-03工况1甲板艉端左舷边位移响应合成、 高频和低频时间历程曲线(15～40 s)Fig.5 Tine series of total, high and low frequency displacement on the port side of the 1st deck trailing edge for case D-03 (15～40 s)

图6 D-03工况1甲板艉端左舷边位移响应的频谱分析图Fig.6 Spectrum of time-displacement waveform on the port side of the 1st deck trailing edge for case D-03

图7～图10 为C-02工况node 32 346位置处位移、速度、加速度和应力响应的频谱分析图。C-02工况中波浪遭遇频率为0.152 9 Hz，频率比γ=0.059，即使是3倍波浪遭遇频率，该船首阶自振频率也是其五倍以上。图7～图9给出了位移、速度和加速度响应频谱图，波频(低频)成分响应分量占比依次减小，反之，伴随自由振动(高频)成分响应分量占比依次增大，图8中可见低频分量几乎为零，说明在频率比比较小(γ<1)时，高频成分在加速度总响应中占比最大，其次是速度响应，再次是位移响应。由于在施加波浪压力时存在常数项，因此图10中在0 Hz处存在一个非零初始值，若仅考虑波动部分，可得应力低频响应与高频响应的占比规律与位移响应规律一致。对C-02工况下node 32 346处各响应衡准参数的时域信号进行滤波，可得到低频波浪诱导的低频振动分量(0.5 Hz以下)和伴随自由振动诱导的高频振动分量(0.5 Hz以上)，表7给出了各响应参数的低、高频成分占比结果，可见伴随自由振动诱导的高频振动成分占比很大，尤其是加速度响应。结合1.3节对单自由度系统中伴随自由振动占比的讨论，结果表明与多自由度的船舶系统相比，各自的伴随自由振动分量占比在量值上存在差异，但总体规律一致。此外，在该船舶系统中，伴随自由振动分量在总响应中占比整体较大，存在“放大”效应。

表6 仿真试验计算的双体船整船总振动频率和振型结果Tab.6 Simulation calculation results of catamaran total vibration frequencies and mode shapes

图7 C-02工况node 32 346位置处位移响应的频谱分析图Fig.7 Spectrum of time-displacement waveform of node 32 346 for case C-02

图9 C-02工况node 32 346位置处加速度响应的频谱分析图Fig.9 Spectrum of time-acceleration waveform of node 32 346 for case C-02

图8 C-02工况node 32 346位置处速度响应的频谱分析图Fig.8 Spectrum of time-velocity waveform of node 32 346 for case C-02

图10 C-02工况node 32 346位置处应力响应的频谱分析图Fig.10 Spectrum of time-stress waveform of node 32 346 for case C-02表7 C-02工况各振动衡准参数中低频、高频成分占比分析(node 32 346)Tab.7 Analysis of the proportion of low and high frequency in each vibration criteria parameters for case C-02(node 32 346)

响应时域最大值0～0.5Hz内的低频成分低频成分占比/%0.5Hz以上的高频成分高频成分占比/%高频成分低频成分位移响应/mm27.499.3934.1618.1065.841.93速度响应/(mm·s-1)325.2917.485.37307.8194.6317.61加速度响应/(mm·s-2)965318.260.199634.7499.81527.64应力响应/kPa2466.61764.2330.981702.3869.022.23

注：分析应力响应低、高频成分占比时仅考虑波动部分。

图11～图13给出了相同波浪参数、不同航速下node 32 346处位移响应，计算工况为A-01、B-01和C-01，遭遇频率分别为0.726 rad/s、0.891 8 rad/s和1.057 7 rad/s，该船顶浪航行的01工况易于激起“两潜体垂向弯曲”模态(模态频率为4.72 Hz)，则频率比依次为γA-01=0.024、γB-01=0.03和γC-01=0.071，从图中可以看出，随着频率比γ的增大高频振动响应所占比重也增大。对时域计算结果进行滤波处理后计算数据见表8。应力响应与位移响应有同样的规律。

表8 A-01、B-01和C-01工况位移响应中低频、高频成分占比分析(node 32 346)Tab.8 Analysis of the proportion of low and high frequency in displacement response for case A-01,B-01 and C-01(node 32 346)

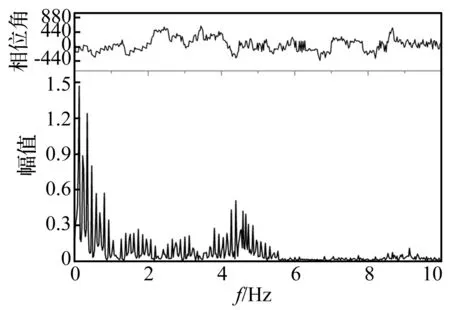
图11 A-01工况node 32 346位置处位移响应的频谱分析图Fig.11 Spectrum of time-displacement waveform of node 32 346 for case A-01

图12 B-01工况node 32 346 位置处位移响应的频谱分析图Fig.12 Spectrum of time-displacement waveform of node 32 346 for case B-01

图13 C-01工况node 32 346 位置处位移响应的频谱分析图Fig.13 Spectrum of time-displacement waveform of node 32 346 for case C-01

4 结 论

目前关于波浪激励下的船舶动响应研究主要集中在砰击振动和波激振动上，然而由低频波浪诱导产生的船体稳态高频振动问题却难以解释。本文从单自由度理论体系出发，对上述高频振动的形成机理进行研究，明确了伴随自由振动在小阻尼体系中短时间内难以衰减的事实。另外，考虑波浪载荷作用于船体时“时变、场变”的特殊性，采用可以将伴随自由振动考虑在内的瞬态响应分析方法，结合NA-1C海浪长期统计资料，对该船在5、6级海况下16个航行工况的振动响应进行预报，分析各振动衡准参数中高频成分占比的相关规律。得到如下结论：

(1)低频波浪所诱导的船体高频振动不易于衰减，是因波浪荷载作用时“时变、场变”的性质所致，加之以船舶是个小阻尼系统，简谐载荷激励所产生的伴随自由振动难以在短时间内衰减，形成相对稳态的高频振动。

(2)在频率比比较低(γ<1)时，由低频波浪载荷激励产生的船体振动响应中，位移、速度、加速度和应力响应均存在显著的高频成分，该成分在各响应中的占比不同，占比最大的是加速度响应的高频成分，其次是速度响应，再次是位移和应力响应。但是，虽然不同振动衡准特征参数响应中的高频成分在比例上有所差别，其量值均没有小到可以忽略的程度。

(3)在相同海况下，波浪遭遇频率的大小线性决定频率比γ的大小，从位移响应计算结果中发现，其振动总响应中的高频成分占比随γ的增大而增大，愈加成为振动的主要成分。进一步分析，随频率比增加，当遭遇频率(或者其较低几阶的倍频)接近船舶自振频率时，船舶可能发生一般意义的非线性波激振动，同时考虑到伴随自由振动不可忽略，那么此时由波浪诱导的高频振动分量则应该认为是伴随自由振动与非线性波激振动的叠加，该结论在理论预报中值得考虑。

因此，这种从伴随自由振动的角度考虑高频振动的方法，为低频波浪激励下的高频波激振动响应研究开发了新思路。

[1] 汪雪良,顾学康,胡嘉骏.船舶波激振动研究进展[J].船舶力学,2013,17(7):830-844. WANG Xueliang, GU Xuekang, HU Jiajun. A state-of-the-art review on ship’s springing investigation [J]. Journal of Ship Mechanics, 2013,17(7):830-844.

[2] 夏齐强，陈志坚，李科技. SWATH船在砰击载荷作用下动态响应研究[J].振动与冲击，2011，30(6)：208-212. XIA Qiqiang, CHEN Zhijian, LI Keji. Dynamic response of SWATH under slamming loads [J].Journal of Vibration and Shock, 2011，30(6)：208-212.

[3] 陈志坚.舰艇振动学[M].北京:国防工业出版社,2010,4: 229-230.

[4] GU X K, SHEN J W, MOAN T. Experimental and theoretical investigation of higher order harmonical components of nonlinear bending moments of ships[J].Journal of Ship Technology Research, Schiffstechnik, 2000, (4): 143-154.

[5] 顾雪康,胡嘉骏.超大型油船模型波浪载荷试验报告[R].无锡：中国船舶科学研究中心科技报告,2004.

[6] 克拉夫 R, 彭津 J. 结构动力学[M]. 北京:高等教育出版社,2006,11:27-34.

[7] 祁皑，范宏伟，陈永祥. 简谐荷载作用下伴生自由振动的研究[J].地震工程与工程振动, 2002,22(6):156-161. QI Ai, FAN Hongwei, CHEN Yongxiang. Research on transient vibration under input of harmonic loading [J]. Earthquake Engineering and Engineering Vibration, 2002, 22(6):156-161.

[8] 戴仰山,沈进威,宋竞正. 船舶波浪载荷[M]. 北京:国防工业出版社,2007,1:11-21.

[9] JENSEN J J. Stochastic procedures for extreme wave load predictions-wave bending moment in ships[J]. Marine Structures, 2009, 22: 194-208.

[10] 刘秀全,陈国明,畅元江,等. 基于频域法的深水钻井隔水管波激疲劳分析[J].振动与冲击,2013,32(11):7-11. LIU Xiuquan, CHEN Guoming, CHANG Yuanjiang, et al. Wave-loading fatigue analysis for deep water drilling risers in frequency domain [J]. Journal of Vibration and Shock, 2013, 32(11):7-11.

[11] 葛菲. 非线性波浪载荷作用下多种应力成份组合的船体结构疲劳强度分析[D].哈尔滨:哈尔滨工程大学,2004.

[12] 缪红燕,高金吉,徐鸿. 转子系统瞬态响应不平衡的有限元分析[J].振动与冲击,2004,23(3):1-4. MIAO Hongyan, GAO Jinji, XU Hong. Transient response of unbalanced rotor system through its critical speed [J]. Journal of Vibration and Shock,2004,23(3):1-4.

[13] 叶永林,席亦农,尤国红,等. 小水线面双体船总振动计算与试验研究[J].中国造船,2011,52(4):56-65. YE Yonglin, XI Yinong, YOU Guohong, et al. Overall vibration calculation and test for swath ship [J]. Shipbuilding of China, 2011,52(4):56-65.

[14] 中国船级社. 小水线面双体船指南(2005)[M].北京：人民交通出版社，2007,2:40-41.

[15] 夏齐强,陈志坚,孙春生. 铝合金穿浪双体船波激振动响应计算研究[J].舰船科学技术,2010,32(2):11-16. XIA Qiqiang, CHEN Zhijian, SUN Chunsheng. A study on wave-induced vibration for aluminum alloy wave piercing catamarans [J]. Ship Science and Technology, 2010, 32(2):11-16.

[16] VIDIC-PERUNOVIC J, JENSEN J J. Non-linear springing excitation due to a bidirectional wave field [J]. Marine Structures,2005, 18: 332-358.

[17] VIDIC-PERUNOVIC J. Springing response due to bidirectional wave excitation[D]. Technical University of Denmark, 2005.

[18] 文圣常,于宙文. 海浪理论与计算原理[M].北京:科学出版社,1985,11:96-101.

Vibration response analysis of ships under wave load based on numerical experiment

TANG Yuhang, CHEN Zhijian, ZHANG Jiadong

(Department of Naval Architecture Engineering, Naval University of Engineering, Wuhan 430033, China)

Even if the slamming vibration and significantly nonlinear wave-induced vibration do not occur, in the vibration response of the hull induced by low-frequency wave load, there still exist high-frequency vibration components, which decay slowly. Based on the harmonic vibration analysis of single-degree of freedom system, it is indicated that the associated free vibration which is often overlooked in the analytical response solution is one of the high-frequency vibration factors. The transient response component is difficult to decay when the system damping is small and natural frequency is low. The occupied proportions of high-frequency components in the responses of displacement, velocity, acceleration and internal force were derived. The “time-changing and field-changing” characteristics of wave loads acting on ships were revealed. It is also shown that the associated free vibration plays an important role in the prediction of vibration responses excited by wave loads. The differences between the results by time domain and frequency domain methods were discussed and the advantages of time-domain methods in dealing with this issue are more prominent. The vibration responses in 16 sailing conditions were forecasted by the numerical simulation of a catamaran, using the wave data. The results show the high-frequency components in the vibration responses are both of steady-state and high-proportion. The relationship between high-frequency components and frequency ratio was obtained, which provides a guideline for the further study on wave-induced vibration in time domain.

associated free vibration; dynamic response; high-frequency vibration;time domain method; nonlinear; wave-induced vibration

国家自然科学基金(51479205)

2015-12-14 修改稿收到日期：2016-03-16

唐宇航 男，博士，1991年生

陈志坚 男，教授，博士生导师，1957年生

TH212；TH213.3

A

10.13465/j.cnki.jvs.2016.22.018