桅杆结构风振系数研究

邓洪洲, 徐海江， 马 星

(1.同济大学 建筑工程系，上海 200092； 2.南澳大利亚大学 自然与建筑环境系，阿德莱德 5095)



桅杆结构风振系数研究

邓洪洲1, 徐海江1， 马 星2

(1.同济大学 建筑工程系，上海 200092； 2.南澳大利亚大学 自然与建筑环境系，阿德莱德 5095)

基于随机风振理论，推导了桅杆结构杆身和纤绳风振系数计算公式；结合高耸结构设计规范的修订，分析了原规范杆身风振系数计算公式存在的问题；基于新荷载规范的改动，给出了杆身风振系数计算方法，更新了纤绳风振系数计算参数表格；通过算例分析发现，杆身振型可按无风状态计算且计算杆身风振系数时可只考虑前四阶振型的贡献；时程分析结果表明，杆身各段取四点计算风振系数的方法精度较好，计算简便；由于新荷载规范提高了脉动风荷载的峰值因子和湍流度，纤绳风振系数增大约20%。

桅杆结构;风振系数;纤绳;高耸结构;设计规范

桅杆结构是由单个杆身和多层斜向布置的纤绳组成的高耸结构，广泛应用于通讯、广播电视等领域，因其刚度小，质量轻，风荷载是主要的控制荷载之一。由于纤绳这种细柔结构的支撑作用，桅杆结构表现出较强的非线性，计算时应考虑纤绳振动对杆身振动的耦合影响[1]。王肇民等[2]通过对纤绳和杆身的动力特性分析，建立了纤绳在不同端部约束情况下平面内、平面外以及弦向自由振动方程，提出了杆身自振特性和桅杆全方位动力刚度的计算方法，并指出纤绳的作用会导致杆身振型在第一层出现负值。风洞试验和风振实测[3-5]结果表明，随着风速的增大，响应谱曲线从能量比较低的稀疏型向能量比较高的连续型变化，结构的非线性程度越来越大，随着风速的增加高阶振型的贡献增加，风振计算中应考虑多阶振型的影响。

国外规范主要采用阵风系数法计算桅杆结构的风振响应。MATERAZZI等[6]通过定义“阵风系数函数”(gust function)对阵风系数法进行了改进并研究了振型数量对响应计算的影响。我国的1990版高耸结构设计规范[7]采用风振系数对桅杆结构静态响应做等效放大，杆身和悬臂段均取单一数值，即高度不同、纤绳层数不同时，风振系数相同，这样的简化与实际不符。2007版高耸结构设计规范[8](以下简称07版规范)采用的杆身风振系数简化计算公式考虑了四阶振型的影响，纤绳风振系数按荷载等效的原则沿全长取等值[9]。

本文结合高耸结构设计规范的修编工作，并根据2012版建筑结构荷载规范[10](以下简称新版荷载规范)相关条文的改动，分析了07版规范中桅杆结构风振系数计算公式在实际工程应用中的一些问题。提出了新的杆身风振系数简化计算公式，推导了纤绳风振系数计算公式，根据新版荷载规范更新了计算表格，勘误了一些内容。最后通过算例给出了桅杆风振系数的计算过程，分析了计算精度。

1 杆身风振系数

1.1 杆身风振系数推导

根据随机风振理论可推导出纤绳平面内对称振动的第j振型的等效风振力[11]：

pdj(x)=ξjujφj(x)m(x)w0

(1)

式中:ξj为第j振型的脉动增大系数，uj为考虑脉动风压和空间相关性的脉动影响系数，x为纤绳沿弦向的局部坐标，φj(x)为第j振型在x处的值，m(x)为纤绳的质量线密度，w0为基本风压。

uj的计算式如下：

(2)

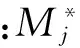
杆身风振系数的计算方法和理论与纤绳相同，只是把沿纤绳长度l的积分改为沿杆身高度H的积分。

由于高阶振型的影响不能忽略，考虑前四阶振型的贡献，并采用平方和开方法(SRSS)求得等效风振力pd(z)。07版规范采用惯性荷载法计算风振系数，并假定迎风面宽度lz(z)、质量线密度m(z)以及体型系数μs(z)沿高度不变，得到风振系数计算公式：

(3)

式中:ps(z)为z高度处的平均风荷载。

1.2 07版规范风振系数讨论

07版规范附录中给出的风振系数计算公式：

(4)

(5)

将式(5)和式(6)代入式(4)的结果与原式(3)完全相同。定义参数ε1w和ε2wn是为了方便编制表格。

为了简化计算，令杆身顶点处各阶振型为1，得到顶点处风振系数计算式：

βz(H)=1+ξε1wε2w

(7)

(8)

对于杆身其它位置，按照第一阶振型调整，即:

βz(z)=1+ξε1wε2wφ1(z)

(9)

式(9)中风振系数沿高度的分布仅与一阶振型φ1(z)有关；但实际上杆身下端的风振响应主要受高阶振型影响且一阶振型可能出现负值，这样按式(9)计算的风振系数就小于1，不符合实际情况。采用四阶振型求和取平均的方法，较规范式(9)有改进，但是意义不明确。由于各阶振型的贡献随高度变化，用φ1(z)表示不合理，如果用等效振型φe(z)替代φ1(z)可能是一条可行的途径，但φe(z)与哪些参数有关、如何取值仍有待研究。

由于杆身高度或纤绳布置等不同时，杆身振型不同，难以归纳。07规范中参数ε2w与高度、地貌、频率和振型等有关，而规范中将影响因素归并为杆身与纤绳的刚度比、纤绳层数等参数，其精确性有待验证，且计算较复杂，不便实际应用。

1.3 风振系数建议式

依据新荷载规范，脉动系数uf(z)和风压高度系数μz(z)的表达式分别为:

(10)

(11)

式中:g，I10，b，α分别为峰值因子，10 m高的湍流度以及地貌类别参数，在新版荷载规范中的取值见表1。

把式(10)、式(11)代入式(3)，整理得到：

(12)

式(12)中含有双重积分，需编程计算，工程应用不便。

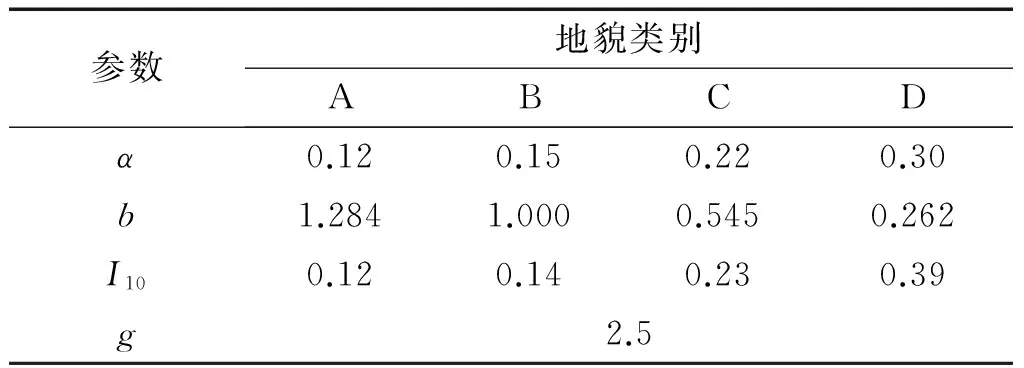
表1 新版荷载规范的参数取值Tab.1 Parameters in new load code

通过多个算例分析发现，杆身各段的风振系数随着高度增加并非单调变化，而是两端小，跨中大。用上下各四分之一点、中点以及上端点即可大概描述出该段风振系数的变化规律。

每段取这些位置的4个点作为参考点，n段共计N=4n个点。为了简化，设每小段的长度为dH=H/N，点的编号自下而上分别为1,2，…，N，则式(12)改写为：

(13)

式中:

(14)

(15)

(16)

式中:φj(i)为第j振型在第i个点所在位置处的值。

由于有限元软件应用的普及，目前在桅杆初步设计时一般已实现整体建模，上述公式中桅杆的振型和自振频率可通过有限元软件进行模态分析得到，这样式(13)中的风振系数就可以采用EXCEL计算，较为简便。

2 纤绳风振系数

由于纤绳的风激振动主要影响纤绳的张力变化，第一振型影响起主要作用。将纤绳沿弦向的积分变为沿高度的积分，式(3)变为:

βz(z)=1+ξεq(z)

(17)

式中:

对于两端铰接的悬索结构，在非均布荷载q(z)的作用下，跨中最大弯矩为：

(19)

假定纤绳的有效宽度为D，当风振系数随高度变化时:

q(z)=(1+ξεq(z))μsμz(z)w0D

(20)

为了简化计算，εq沿纤绳全长取等值，此时:

q(z)=(1+ξεq)μsμz(z)w0D

(21)

将式(20)、式(21)分别代入式(19)中并令跨中弯矩相等，利用纤绳一阶振型关于跨中对称的性质，求得等效εq的计算式为:

(22)

式中:纤绳一阶振型的表达式为:

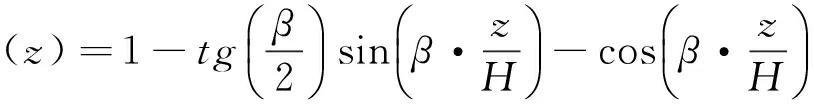
(23)

(24)

而λ2与β存在对应关系:

(25)

由于新荷载规范的改动，εq的取值也相应进行了调整(见表2)。表中变化范围的数字是A类至D类地貌，B类取该数字范围约为0.1处，C类取0.5处。由于350 m以上数值变化很小，此处不再列出。由式(22)及表1可以看出，εq的变化主要取决于峰值因子g与10 m高的湍流度I10，由于新荷载规范提高了峰值因子和湍流度，A类至D类地貌εq增加了40%～60%。

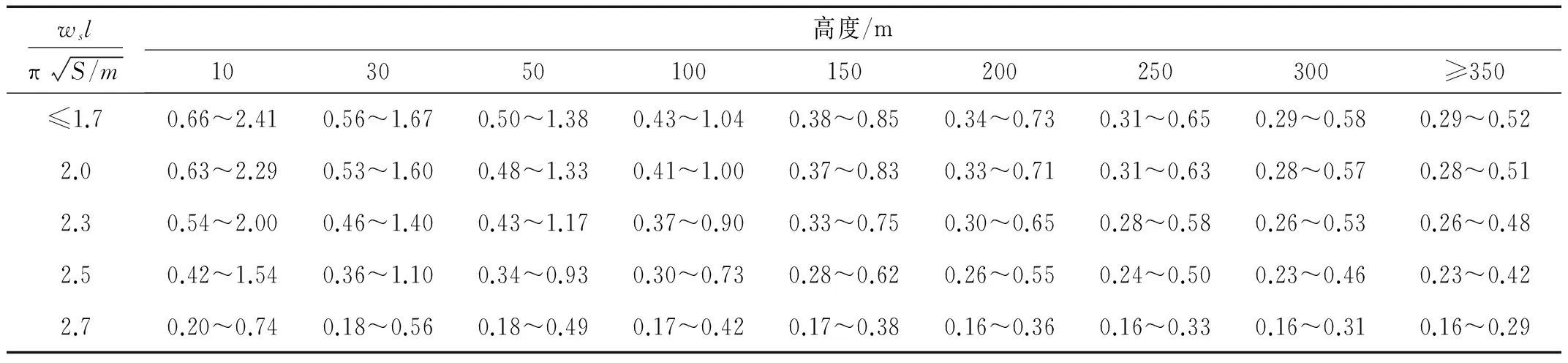
表2 综合考虑风压脉动、高度变化及振型影响的系数εqTab.2 Coefficient εq in comprehensive consideration of wind pressure fluctuation, height and modes

3 实例分析

3.1 基本参数

本文以一个三层三方纤绳的桅杆(见图1)为例，比较了采用计算公式和时程模拟得到的风振系数。桅杆高度为156.1 m，杆身为圆钢组合构件，断面为等边三角形，宽1.5 m，弹性模量E=2×105N/mm2，各层纤绳的直径均为30 mm，弹性模量为Ek=1.2×105N/mm2，初应力σ0=250 N/mm2；基本风压w0=1.0 kN/m2，B类地貌，风向角为0°。

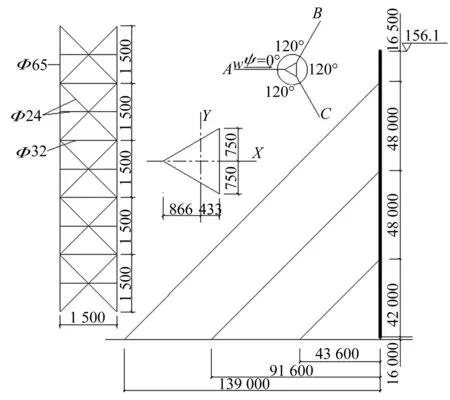
图1 桅杆的几何参数Fig.1 Geometry of the guyed mast

3.2 公式计算结果

桅杆自振频率密集，为确定杆身自振特性，先采用Ansys软件建立杆身-弹簧模型，将纤绳作用简化为弹簧，由模态分析得到杆身自振频率，再建立杆身-纤绳模型，找出对应的最接近的频率及相应的振型。

纤绳的静力刚度包含纯粹弹簧刚度和纤绳瞬时几何刚度两部分，不同工况(无风，基本风速分别为24 m/s，30 m/s，36 m/s和40 m/s)下纤绳的刚度见表3。随着风速的增加，纤绳刚度减小，其中第三层纤绳刚度降幅最大，减小了约55%。

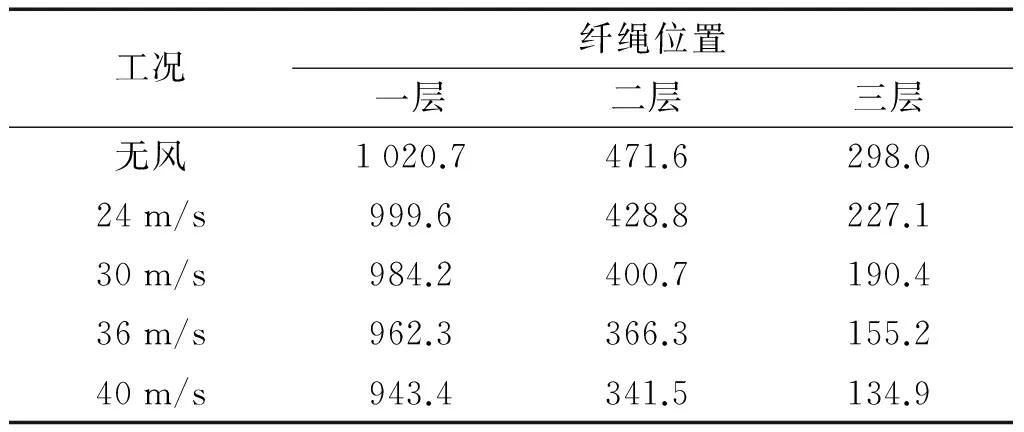
表3 不同工况下纤绳刚度Tab.3 Stiffness of cables under different conditions kN/m

通过模态分析得到的不同工况下杆身自振频率见表4。随着风速的增加，虽然纤绳刚度变化较大，但是，杆身自振频率变化很小，且杆身前三阶振型变化幅度很小，四至六阶振型基本重合(限于篇幅此处振型未列出)，故可以用无风时的杆身自振特性替代。

表4 不同工况下杆身自振频率Tab.4 Frequencies of rod under different conditions Hz

风速为40 m/s时的杆身前四阶振型如图2所示。从图中可以看出，下端一阶振型存在负值，与前面的分析一致。

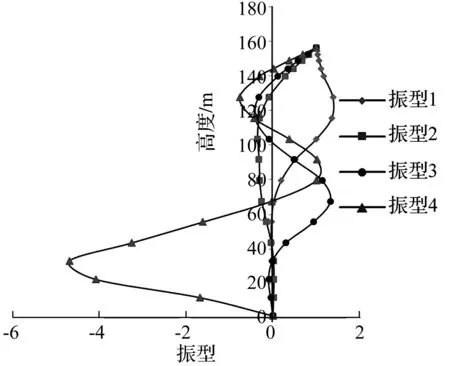
图2 桅身前四阶振型Fig.2 First four modes of mast

不同工况下杆身风振系数按式(13)计算结果如图3所示。由上述分析可知，随着风速的增加，杆身风振系数增大的主要原因是脉动增大系数ξj的变化。随着高度的增加，杆身风振系数并不单调增加，而是在各段端点处取值最小，跨中取值最大，曲线呈S形。

根据式(3)用Matlab软件编写了风振系数计算程序，并分别计算了考虑前几阶振型的结果。表5中列出了分别考虑前三阶、四阶、五阶和六阶振型时杆身风振系数计算结果。五阶与六阶计算结果非常接近，故以下不再考虑更多振型。与六阶振型值相比、仅取前三阶振型时杆身上端风振系数相差很小，但下端风振系数相差可达50%以上，表明杆身上端风振响应主要受低阶振型控制，而下端风振响应则受高阶振型的影响；而与六阶相比，取前四阶振型计算时误差均约在3%以内。说明取前四阶振型计算杆身的风振系数已能保证一定精度。

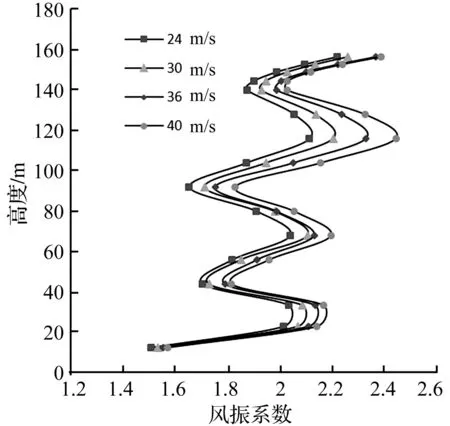
图3 不同工况下的杆身风振系数Fig.3 Wind vibration coefficient of mast under different conditions

为了验证式(13)计算结果的精确性，采用AR法模拟了杆身和纤绳上共计506个点的脉动风速，脉动风速谱采用Davenport谱，空间相关系数采用与频率无关的Shiotani相关系数，考虑了横向与竖向的空间相关性。脉动风速时间间隔为0.1 s，共模拟了600 s的风速数据，10 m高处脉动风速时程曲线见图4。

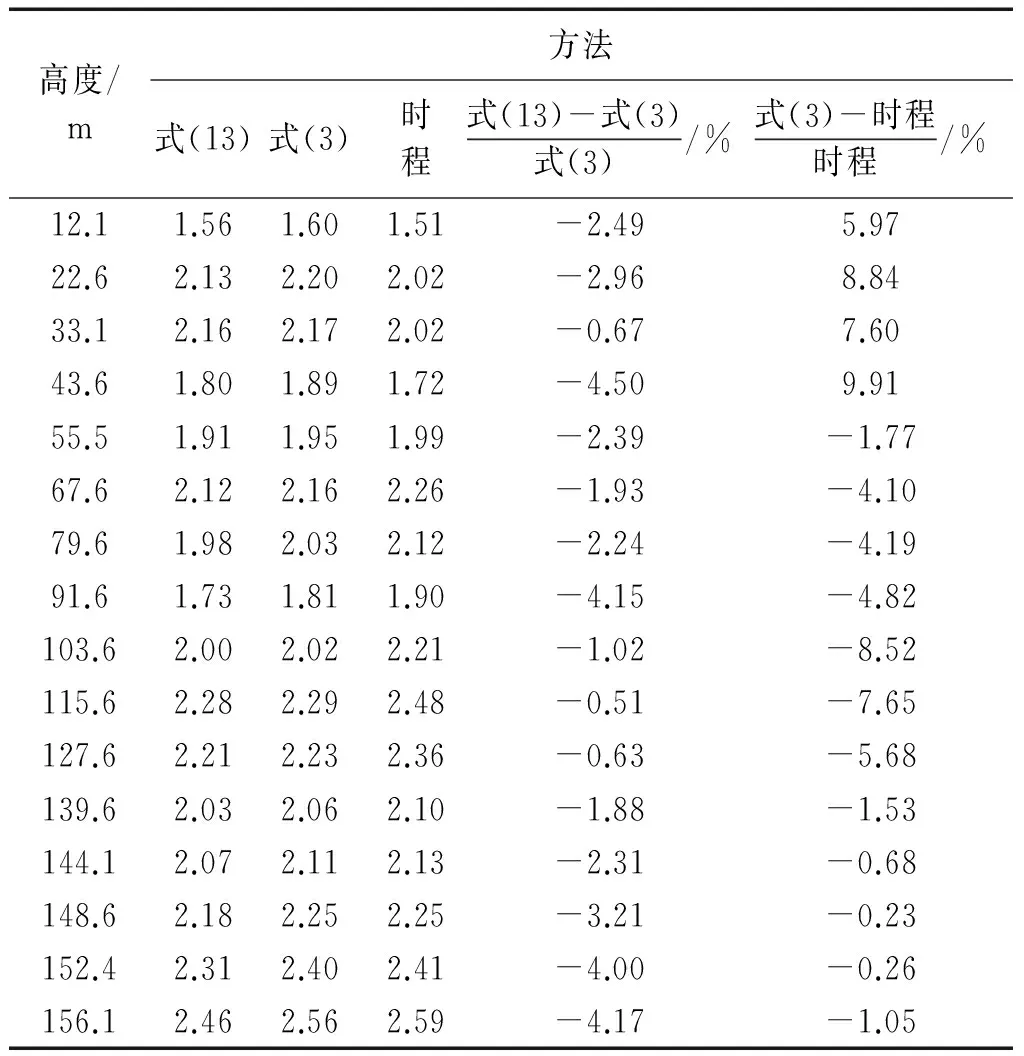
通过Ansys时程分析得到杆身各点的加速度响应时程，并采用惯性荷载法计算了各点的风振系数。表6比较了分别采用简化式(13)，式(3)考虑前四阶振型和时程模拟得到的风振系数计算结果。式(3)与式(13)的误差在5%以内，说明新的简化计算公式精度较好。而与时程模拟相比，按照新的简化计算公式计算的杆身风振系数下端偏大，上端偏小，误差均在10%以内，也具有较好的精度。

表5 振型数量对风振系数计算的影响Tab.5 Influence of The number of modes considered to the calculation of wind vibration coefficient

图4 10 m高度处脉动风速时程曲线Fig.4 Time history of wind velocity at the height of 10 m表6 公式计算与时程模拟得到的风振系数比较Tab.6 Comparison of wind vibration coefficient using calculation formula and time-domain method respectively

高度/m方法式(13)式(3)时程式(13)-式(3)式(3)/%式(3)-时程时程/%12.11.561.601.51-2.495.9722.62.132.202.02-2.968.8433.12.162.172.02-0.677.6043.61.801.891.72-4.509.9155.51.911.951.99-2.39-1.7767.62.122.162.26-1.93-4.1079.61.982.032.12-2.24-4.1991.61.731.811.90-4.15-4.82103.62.002.022.21-1.02-8.52115.62.282.292.48-0.51-7.65127.62.212.232.36-0.63-5.68139.62.032.062.10-1.88-1.53144.12.072.112.13-2.31-0.68148.62.182.252.25-3.21-0.23152.42.312.402.41-4.00-0.26156.12.462.562.59-4.17-1.05

根据本文给出的表2计算出的纤绳风振系数结果见表7，对于同层纤绳，方位不同时一阶自振频率相差较小，因而风振系数变化很小。由于新版荷载规范中峰值因子和湍流度的增加使得修订后的纤绳风振系数提高了约20%左右。

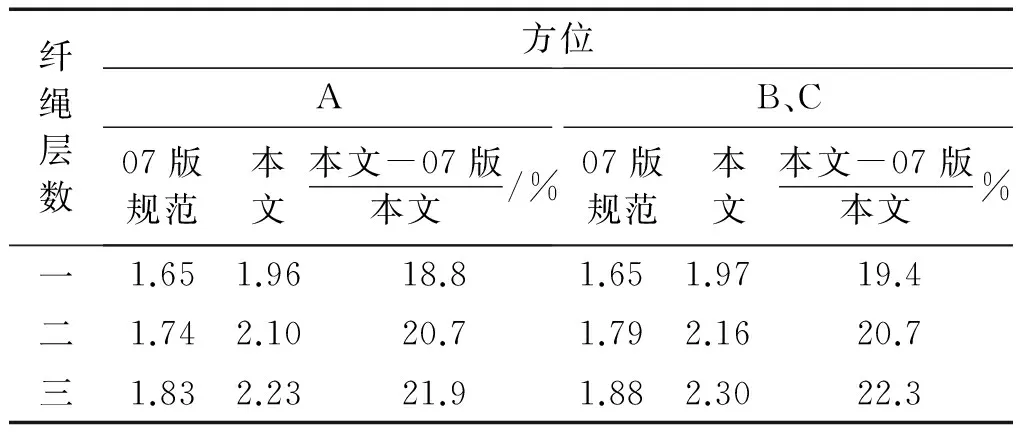
表7 纤绳风振系数Tab.7 Wind vibration coefficient of cables

4 结 论

本文较为详细地推导了桅杆杆身及纤绳的风振系数计算公式，更新了纤绳参数的表格，讨论了07版规范的问题并提出了新的杆身风振系数简化计算公式。经过理论分析和算例计算比较得出以下结论：

(1)风荷载对纤绳刚度有较大影响，但是对杆身自振特性影响较小，可用无风荷载作用时的杆身自振特性替代，自振特性可通过有限元软件建模分析得到。

(2)杆身下端风振响应受高阶振型影响，上端受低阶振型影响，风振系数计算时可只考虑前四阶振型的影响。

(3)杆身各段风振系数呈凸形，两端小，跨中大，总体随高度呈增加趋势，采用杆身各段取四个点的简化计算方法满足一定精度，且计算简便，适合工程应用。

(4)新版荷载规范提高了峰值因子和湍流度，桅杆的风振系数有一定增大，纤绳风振系数增大20%左右。

[1] 王肇民.桅杆结构[M].北京:科学出版社,2001.

[2] 王肇民,程勇凌.桅杆结构动力特性研究[J].建筑结构学报,1993, 14(5):2-10.

WANG Zhaomin, CHENG Yongling. Research on dynamic characteristics of guyed mast structure[J]. Journal of Building Structures,1993, 14(5):2-10.

[3] 王仲刚,邓洪洲,王肇民. 桅杆风振试验研究[J]. 工程力学,2003, 20(5):42-47. WANG Zhonggang, DENG Hongzhou, WANG Zhaomin. Experimental study of the dynamic behavior of guyed mast in wind tunnel[J]. Engineering Mechanics,2003, 20(5):42-47.

[4] 王肇民,何艳丽,马星, 等.桅杆结构风洞试验研究[J]. 建筑结构学报,2000, 21(6):55-61. WANG Zhaomin, HE Yanli, MA Xing, et al. Research on wind tunnel experiment of guyed masts[J]. Journal of Building Structures, 2000, 21(6):55-61.

[5] 邓洪洲,徐建波,黄健,等. 桅杆结构动力特性及风振响应实测[J]. 同济大学学报(自然科学版),2004,32(10):1289-1294. DENG Hongzhou, XU Jianbo, HUANG Jian, et al. Full scale measurements of dynamic behavior and wind-induced response of guyed masts[J]. Journal of Tongji University(Natural Science),2004,32(10):1289-1294.

[6] MATERAZZI A L, VENANZI I. A simplified approach for the wind response analysis of cable-stayed masts[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2007,95:1272-1288.

[7] 高耸结构设计规范: GB J135—1990[S]. 北京:中国建筑工业出版社,1991.

[8] 高耸结构设计规范: GB 50135—2006[S]. 北京: 中国计划出版社,2007.

[9] 马星,颜明忠,沈之容. 桅杆结构风振系数简化计算[J].特种结构,2002, 19(3):54-56. MA Xing, YAN Mingzhong, SHEN Zhirong. Simplified wind vibration coefficient of guyed mast structure[J]. Special Structures,2002, 19(3):54-56.

[10] 建筑结构荷载规范: GB 50009—2012[S]. 北京: 中国建筑工业出版社,2012.

[11] 王肇民,程勇凌.桅式结构的风振系数研究[J]. 同济大学学报(自然科学版),1994, 22(2):178-183. WANG Zhaomin, CHENG Yongling. Research on wind vibration coefficient of guyed mast structures[J]. Journal of Tongji University(Natural Science),1994, 22(2):178-183.

Wind-vibration coefficient of guyed masts

DENG Hongzhou1, XU Haijiang1, MA Xing2

(1. Department of Structural Engineering, Tongji University, Shanghai 200092, China;2. School of Natural and Built Environments, University of South Australia, Adelaide 5095, Australia)

The calculation formulae for the wind vibration coefficients of masts and cables were deduced on the basis of random vibration theory. The inadequacy about the wind vibration coefficient in the design code of high-rising structures together with the resision of the code were discussed. A new formula was proposed and the parameter`s table was re-established on the basis of the revision of load code for designing building structures. The analysis of examples shows that the modes of masts can be calculated under the assumed condition of no-wind state and the first four modes need to be taken into account. The time-domain analysis results prove that the method of using four points in each section is precise enough and convenient to use. Due to the increase of the peak factor and turbulence intensity in the new code, the wind vibration coefficient of cables increases by approximately twenty percent.

guyed mast; wind-vibration coefficient; cable; high-rising structure; design code

国家自然科学基金项目资助(51578421)

2015-01-16 修改稿收到日期：2015-03-20

邓洪洲 男，教授，博士生导师，1960年生

徐海江 男，博士生，1992年生

TU392.6；TU311.3

A

10.13465/j.cnki.jvs.2016.22.008