非对称大惯量刚性磁悬浮高速转子陀螺效应自适应抑制方法研究

沈易霏， 韩邦成 ， 郑世强

(1.北京航空航天大学 惯性技术重点实验室，北京 100191； 2.北京航空航天大学 新型惯性仪表与导航系统技术国防重点学科实验室，北京 100191；3.北京市高速磁悬浮电机技术及应用工程技术研究中心，北京 100191)



非对称大惯量刚性磁悬浮高速转子陀螺效应自适应抑制方法研究

沈易霏1,2， 韩邦成1,2， 郑世强1,2

(1.北京航空航天大学 惯性技术重点实验室，北京 100191； 2.北京航空航天大学 新型惯性仪表与导航系统技术国防重点学科实验室，北京 100191；3.北京市高速磁悬浮电机技术及应用工程技术研究中心，北京 100191)

针对磁悬浮分子泵中非对称大惯量刚性磁悬浮转子高速运行时出现的涡动模态失稳的问题，建立了非对称刚性转子的动力学模型，并提出了一种针对非对称转子的转速自适应的多通道单边滤波PIDC控制方法，在不同的转速段内自动切换反馈通道，通过优化预调参数对转子远离质心一端出现的涡动模态失稳的现象进行相位补偿，仿真结果表明，这种PIDC控制算法简单易用，可以有效解决高速下陀螺效应导致的转子一端进动和章动模态失稳的问题。通过实验验证了该方法的可靠性，分子泵样机平稳升速到21 000 r/min，样机达到了设计真空性能指标。

非对称；陀螺效应；转速自适应；多通道单边滤波；PIDC控制

磁悬浮轴承是利用电磁力使转子悬浮的高性能非接触式轴承，相比于传统的机械轴承，拥有转速高、能耗低、无机械磨损、噪声小、无润滑介质、寿命长、控制灵活等一系列突出的优点，被广泛应用于冶金工业、航空航天[1-2]等领域。对磁轴承系统的转子来说，通常情况下，在压缩机、鼓风机及分子泵[3]等旋转机械中常常带有大量的叶片。转子带叶片后，由于叶片与转子的相互作用，为了获得更加准确的转子动力学模型，有必要将叶片、转子和磁轴承看成一个整体[4]，在转子高速旋转时，磁悬浮轴承系统的控制对象就变成非对称大惯量高速转子系统，因此，除了要在原理上解决磁轴承支撑叶片转子系统动力学模型的建立问题[5]，还要在控制上解决由于陀螺效应所导致的大转动惯量比、高速转子进动和章动失稳的问题[6]，特别对于磁悬浮复合分子泵这种为科学研究提供超洁净和超高真空环境的机械设备，这一问题显得尤为突出。

针对大惯量比转子随转速升高出现强陀螺效应这一问题，已提出了很多种抑制方法。一类是以现代控制理论为基础的控制方法，其基本思想是根据闭环系统设计要求设计补偿反馈控制器，在动态过程中，根据系统当前状态有目的地不断变化，迫使系统按照预定状态轨迹运动。如滑模控制[7]、LQR控制[8]、线性状态反馈解耦控制[9]、Gain-ScheduledH∞控制[10]、μ综合[11]、Cholesky分解降阶[12]等，但这类算法一般来说都需要采用数字处理器实现，由于运算量较大,工程实现上具有一定的难度。而另一类则是传统的各类交叉反馈控制方法，其基本思想是在分散控制的基础上，再附加另外的反馈通道以补偿陀螺效应。其中又分为比例交叉[13]、微分交叉[14]、比例微分交叉[15]和任意超前角构造交叉[16]等几种类型。自AHRENS等[17]提出交叉控制的概念以来，由于控制方法简单直接，已经在工程上得到了广泛应用。此类方法相较于分散控制算法的规模与大小没有太大的扩展,易于实现，并且运算时间较短，大约只有线性状态反馈解耦控制运算时间的四分之一，而且交叉反馈通道的增益可以很容易地由转子系统的物理参数确定，缩短了转子系统稳定控制的调试周期。

在带叶片转子系统建模问题上，针对传统机械转子系统，王立刚等[18]利用GENTA[19]提出的圆型单元谐波有限元模型方法将叶片模化成单摆结构，分析了系统中叶片的轴向振动、扭转振动和弯曲振动的动力学特性和叶片-转子-轴承系统的耦合非线性动力特性，这样的简化使问题得到了解决。由于本文研究对象为磁悬浮分子泵的转子，设计要求转子最高工作转速与第一阶挠曲临界转速之比小于0.7，所以对平衡而言转子是刚性的。因而在针对磁悬浮叶片-转子-轴承系统建模的过程中，可以对叶片和转子釆用线性处理，即采用传统的转子动力学建模方法足以保证系统与动力学模型的精度。

对于高速下大惯量转子涡动模态失稳的问题，本文提出了一种针对非对称转子的转速自适应的多通道单边滤波PIDC控制方法，可以对非对称转子远离质心一端的章动和进动模态进行相位补偿，仿真与实验结果表明，这种PIDC控制算法简单、易于工程实现，可以有效地控制非对称大惯量刚性高速转子陀螺效应导致的涡动模态失稳。

1 非对称大惯量磁悬浮转子系统动力学建模

针对设计的磁悬浮复合分子泵复合转子进行受力分析，磁轴承支承转子受力情况如图1所示。

图1 非对称大惯量刚性转子受力分析Fig.1 Force analysis of asymmetric rigid rotor with large inertia

理想情况下，转子的轴线在两径向轴承的中心连线上。为了描述转子、传感器和主动电磁轴承间的相互位置，建立了主坐标系，其中坐标原点在复合转子理想位置的质心O点，z轴在两径向轴承中心连线上，x轴和y轴与z轴之间形成右手坐标系。上下传感器到O点的距离分别为lsa和lsb，上下径向电磁轴承A和B的中心到O点的距离分别为lma和lmb，为了便于分析另外建立了三个径向平面的坐标系，分别是传感器坐标系、主动电磁轴承坐标系以及质心坐标系。转子在发生运动时，转子质心的坐标分别为xI、yI、αI及βI，上下传感器处的坐标分别为xsa、xsb、ysa、ysb，上下电磁轴承处的坐标分别为为xma、xmb、yma、ymb。

根据转子动力学理论，容易写出偏心非对称电磁悬浮刚性转子系统的运动方程为:

(1)

式中:m为偏心转子的质量，Jx=Jy为转子绕x及y轴的转动惯量，Jz为转子绕z轴的转动惯量。fax、fbx、fay、fby分别为A及B端主动电磁轴承在x和y方向上的电磁力。

由式(1)可以得到径向电磁轴承刚性转子系统传递函数的框图如图2所示。

图2 非对称刚性转子系统传递函数Fig.2 Transfer function of asymmetric rigid rotor

由图2可知,两个转动自由度α和β之间是相互耦合的，耦合影响的大小与Jz/Jx、Jz/Jy以及转频的大小Ω有关。将式(1)写为矩阵形式：

(2)

其中,非对称转子系统的广义质量矩阵为:

M=diag(m,Jy,m,Jx)

陀螺效应矩阵和力臂系数矩阵分别为:

主动电磁轴承的电磁力向量和非对称刚性复合转子质心的坐标向量分别为:

将经典的磁悬浮轴承电磁力公式经线性化后写成矩阵形式可得：

fm=Kmqm+Kiu

(3)

其中，主动电磁轴承相对平衡点的位移矩阵、控制电流矩阵、磁轴承位移刚度系数矩阵、磁轴承电流刚度系数矩阵分别为:

在主动电磁轴承的结构参数和偏置电流和间隙确定后，主动电磁轴承的电流刚度系数和位移刚度系数都是常数。将式(3)代入式(2)，可得：

(4)

为了统一坐标系，将式(4)右边的磁轴承坐标系qm转换为质心坐标系qI。可得到坐标转换关系为:

qm=TmqI

(5)

式中:Tm为执行器坐标到质心坐标的转换矩阵。经过观察可以看出，矩阵Tm是矩阵Tf的转置，即Tm=TfT。将式(5)代入式(4)可得：

(6)

令Kmm=-TfKmTfT，整理上式可得：

(7)

对非对称转子使用传统的分散PID控制，在控制模型中不考虑积分环节，低通和陷波环节，并且忽略控制器、功放和传感器等环节时间延迟效应，控制电流可表示为:

(8)

式中:Kp、Kd、Ks、Kw、Kad分别比例控制矩阵、微分控制矩阵、位移传感器位移电压系数矩阵、功放增益系数矩阵和AD转换系数矩阵。简化的控制模型参数如下：

将式(8)代入式(7)得：

(9)

式中：

2 控制系统采用分散PID控制时的仿真分析

跟据以上推导建立非对称大惯量刚性磁悬浮转子系统模型，采用分散PID控制时，由于闭环系统存在相位延迟和积分环节，转子涡动模态阻尼会恶化，涡动模态的稳定性成为影响转子系统转速进一步提高的障碍。为了验证这一现象，根据在实验中实际设置的控制器参数(见表1)和实际被控对象(功放环节+超高真空大抽速磁悬浮复合分子泵磁轴承)的参数(见表2)，通过Matlab进行仿真分析。

表1 实验中磁轴承控制系统实际参数Tab.1 The actual parameter of magnetic bearing control system in practical experiment

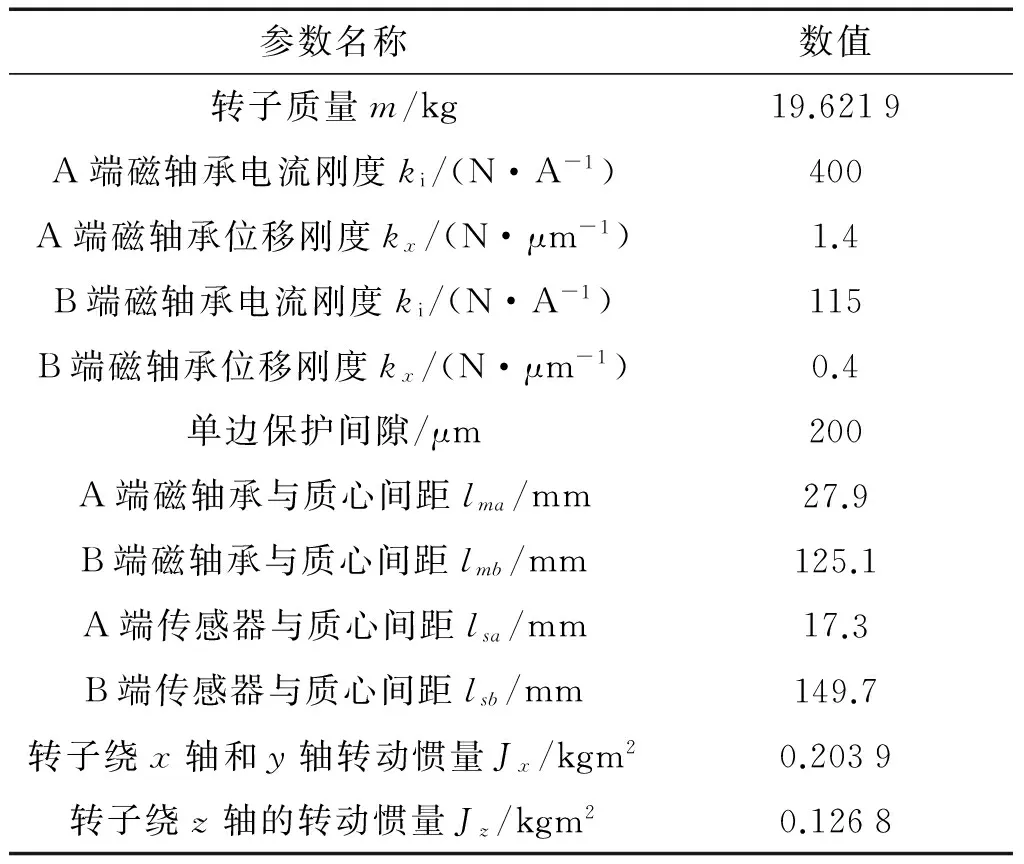
表2 实际被控对象参数Tab.2 The parameters of actual controlled objects

转子在低速时稳定，当转频升至135 Hz时。由图3(a)和图3(b)可知，转子下径向出现不稳定的趋势，B端位移信号除转速同频振动外还出现了频率为4 Hz的包络曲线，动态仿真显示，此低频涡动的方向与转子转动方向相反，可知由于积分系数增大，转子质心远端在升速的过程中率先出现进动模态失稳。

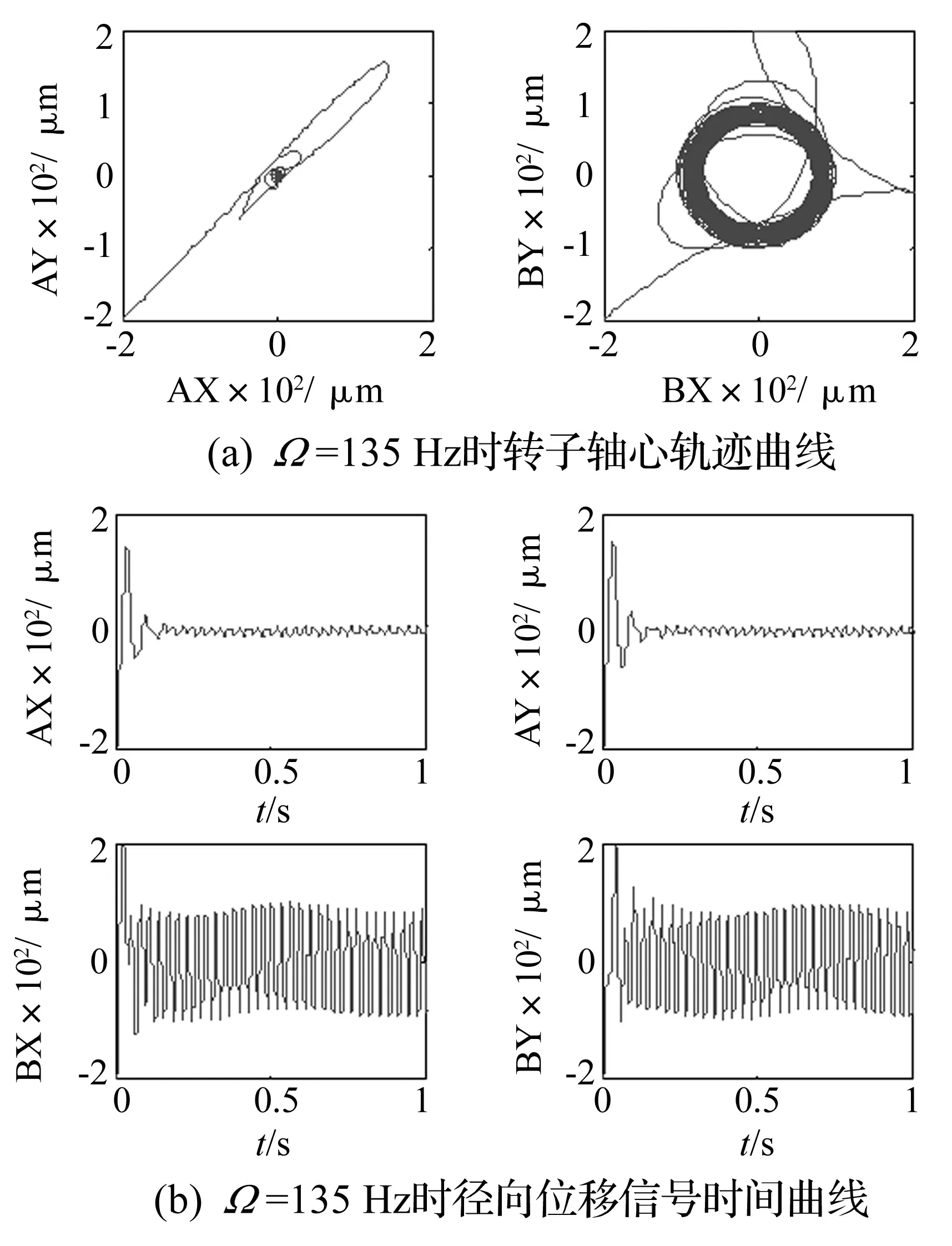
图3 Ω=135 Hz时转子运动状态Fig.3 The kinstate of the axis when Ω=135 Hz

去掉积分环节使转子进动模态稳定，转频升至158 Hz时。由图4(a)和图4(b)可知，B端转子出现明显的频率为134 Hz的高频发散振荡，由于此转子轴径向转动惯量比小于1，可推知章动频率小于同频，所以由高速时章动频率与转频的关系推知是章动失稳，振幅达到200 μm，可知B端已经碰撞保护轴承，而A端轴心轨迹仍然收敛。这说明由于加叶片的原因，此分子泵转子的质心基本与上径向磁轴承中心重合，质心为三转动自由度惯性主轴的交点，在转角一定的情况下，离质心越远的一端，振动幅度越大，进而可推断出其失稳时的程度越大。

由于未考虑陀螺力，使用分散PID控制器时，非对称系统远离质心的一端在高速转动下会率先出现进动失稳，随着转速的增加，章动模态失稳也会立刻出现，陀螺效应的存在会使这一端的稳定裕量越来越小。

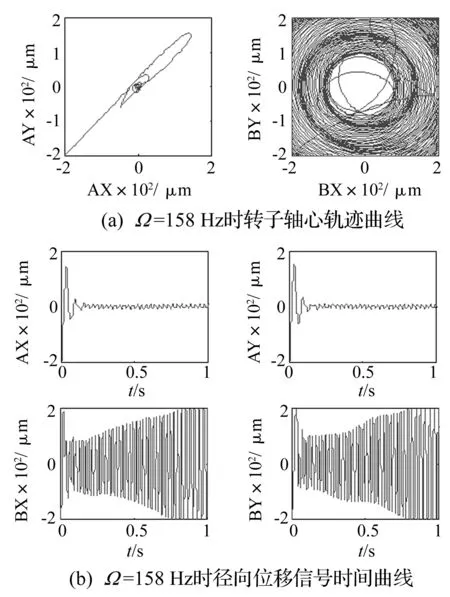
图4 Ω=158 Hz时转子运动状态Fig.4 The kinstate of the axis when Ω=158 Hz

此结果表明，采用分散PID控制无法满足非对称大惯量刚性磁悬浮转子高速稳定悬浮控制的需求。对于B端首先出现的涡动模态失稳，必须有针对性地对其予以相位补偿以增大其失稳涡动模态的阻尼。

3 转速自适应的多通道单边滤波PIDC控制

在解决陀螺效应的问题上，如果直接在PID基础上通过添加更复杂的滤波器，调整PID控制器的增益与相位特性。当转子转速不太高，通过这种方法增加控制器增益和阻尼比是可行的。但磁轴承带宽要提高，以在大的频率范围内满足章动与进动阻尼需求，会造成控制器增益过高，导致那些阻尼不够强的叶片结构的振动模态被激发出来。此时仅仅依靠局部通道分散控制器的参数调整来抑制它们非常困难。

而交叉反馈控制方法对转子模型有很好的适应性，所以本文采用转速自适应的多通道单边滤波PIDC(PID and Cross Feedback)控制方法的基本思路如图5所示。

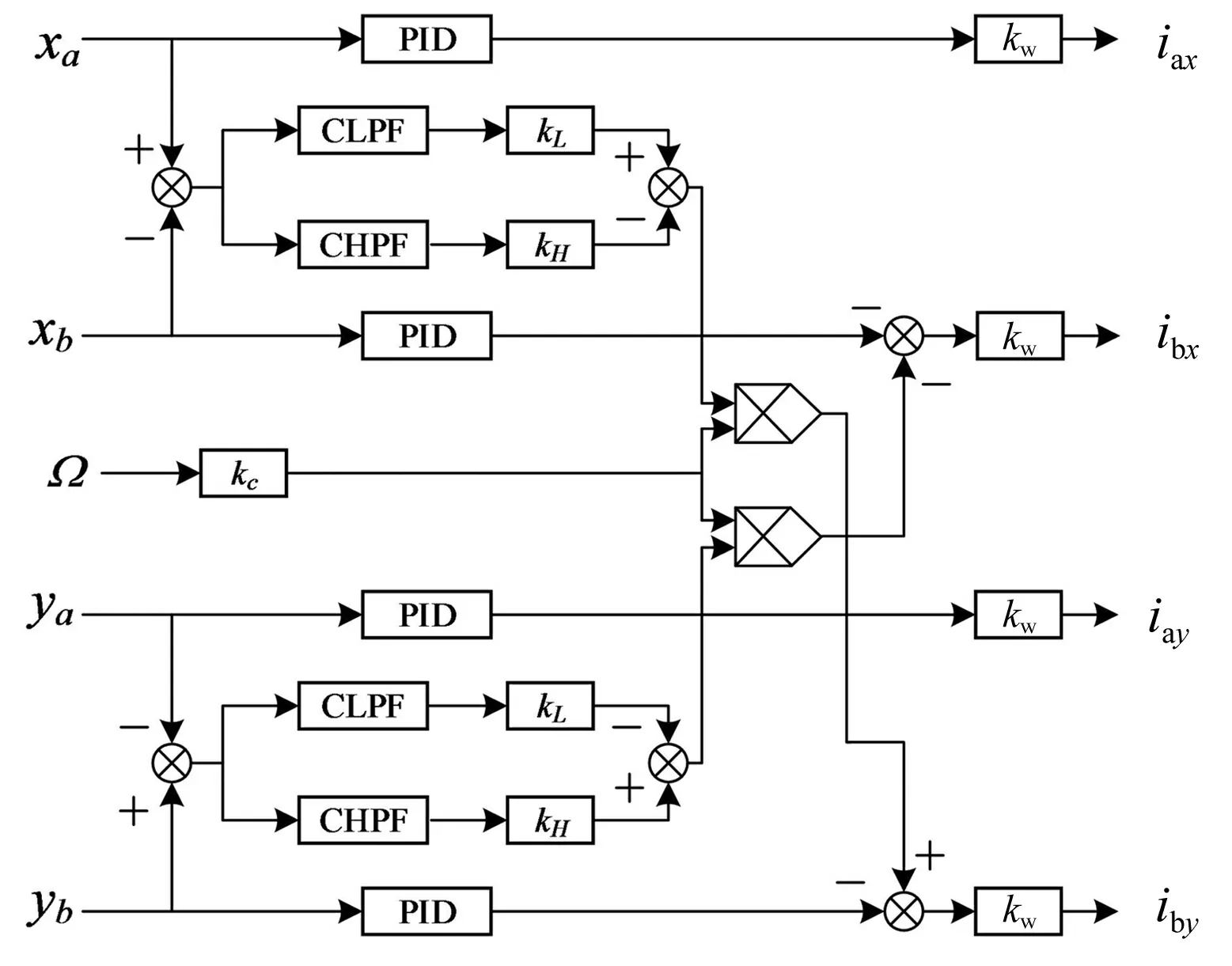
图5 转速自适应的多通道单边滤波交叉反馈控制Fig.5 Speed-adaptive multi-channel unilateral filtering PIDC

在分散PID控制器基础上，将各通道径向位移信号的差分送到交叉反馈控制模块，利用进动模态和章动模态在频率上的差异，用CLPF(交叉低通滤波器Cross Low Pass Filter)和CHPF(交叉高通滤波器Cross Low Pass Filter)对信号进行分离，然后根据章动和进动各自的涡动方向，分别对非对称转子质心远端进动模态和章动模态实现交叉相位补偿，由于进动和章动的运动方向相反，所以在实际的控制中，章动交叉和进动交叉的控制信号在极性上相反。另外考虑到陀螺耦合力矩和转速成正比，以及进动频率随转速下降和章动频率随转速上升的特点，在交叉控制通道中引入了与转速信号成正比的交叉比例系数kc，以保证转子系统在不同的转速时的稳定性。

由于质心远端首先出现进动模态失稳，所以必须在这一端引入PIDC控制，首先调整CLPF的截止频率和增益kL以补偿控制系统在这一端的低频段的相位滞后。待系统稳定后，再次升速会出现章动模态的失稳，这时应调整CHPF的截止频率和增益kH来补偿高频段的相位滞后。加入转速自适应的多通道单边滤波PIDC方法的的系统控制结构如图6所示。

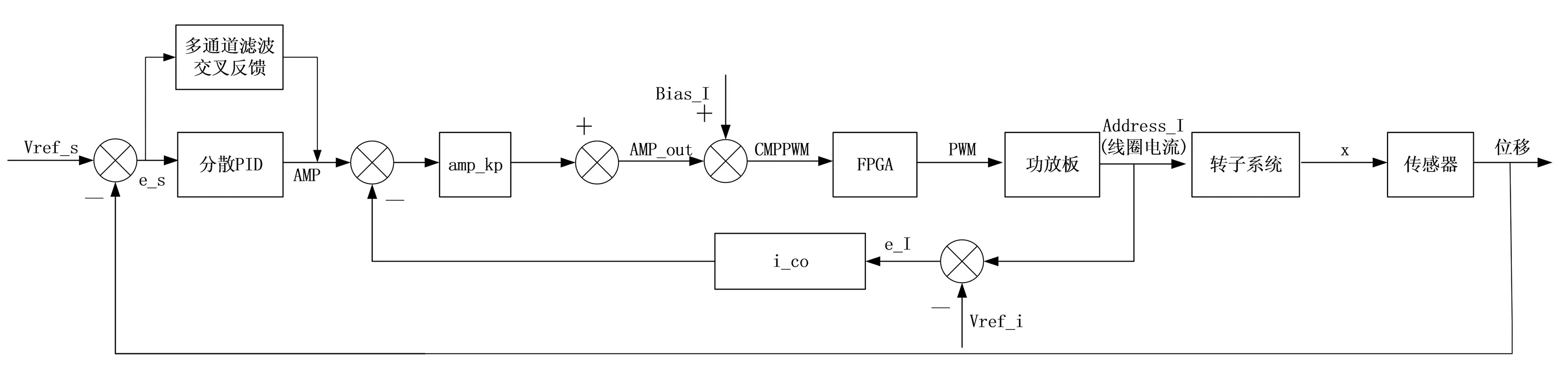
图6 磁轴承控制系统结构框图Fig.6 Scheme of magnetic bearing control system

由于造成下端转子在高速下失稳的主要原因是章动模态的稳定性，所以为保证转子继续升速到额定转速的整个过程中，都能有足够的稳定裕度，可以跟随转速采用分段调整CHPF的截止频率和kH的方法对这一端的章动模态进行自适应相位超前补偿，实现全转速高稳定性悬浮。通过提高章动交叉的截止频率，可以提供更多的相位补偿，采用跟随转速在截止频率不同的多级CHPF通道之间切换的方法(见图7)，来实现不同转速下的章动阻尼补偿，从而大幅度提高系统质心远端的章动稳定性。

图7 章动模态转速自适应交叉控制模块原理框图Fig.7 The diagram of speed-adaptive cross control block for nutation mode

使用数字控制器时，章动交叉通道采用跟随转速升高，CHPF截止频率由低到高多级切换的滤波方式，其切换方式如图8，CHPF截止频率从1～5依次升高，转速从Fr1～Fr4也依次升高，将全转速区间离散成不同的转速段，在不同的转速段内，采用截止频率不同的CHPF通道，从而实现转速自适应的多通道单边滤波PIDC控制。

图8 章动模态转速自适应交叉控制多级切换方法Fig.8 Multi-stage switching method of speed-adaptive cross control for nutation mode

4 下端径向磁轴承加入PIDC控制的仿真分析

当转频升至135 Hz时，在下端径向磁轴承控制器中加入交叉比例kc=0.8和进动交叉，其中CLPF为二阶，截止频率为30 Hz，CLPF增益kL=0.75，之后B端转子轴心轨迹立刻恢复收敛。继续升速直到转频为158 Hz时，B端转子出现剧烈的高频振动，在下端控制器中加入章动交叉，其中CHPF1也为二阶，截止频率为150 Hz，CHPF1增益kH=1.8，章动模态恢复稳定。继续将转频升至239 Hz，下端转子章动再次出现失稳，此时切换CHPF通道，截止频率和增益kH分别为200 Hz和1.73，系统再次恢复稳定。此后依次在出现章动失稳模态时切换CHPF通道(见表3)，使用此控制方法成功升至转子额定转频350 Hz，B端位移仅为21μm(见图9(a)、图9(b))。仿真结果表明转速自适应的多通道单边滤波PIDC控制方法是有效的。

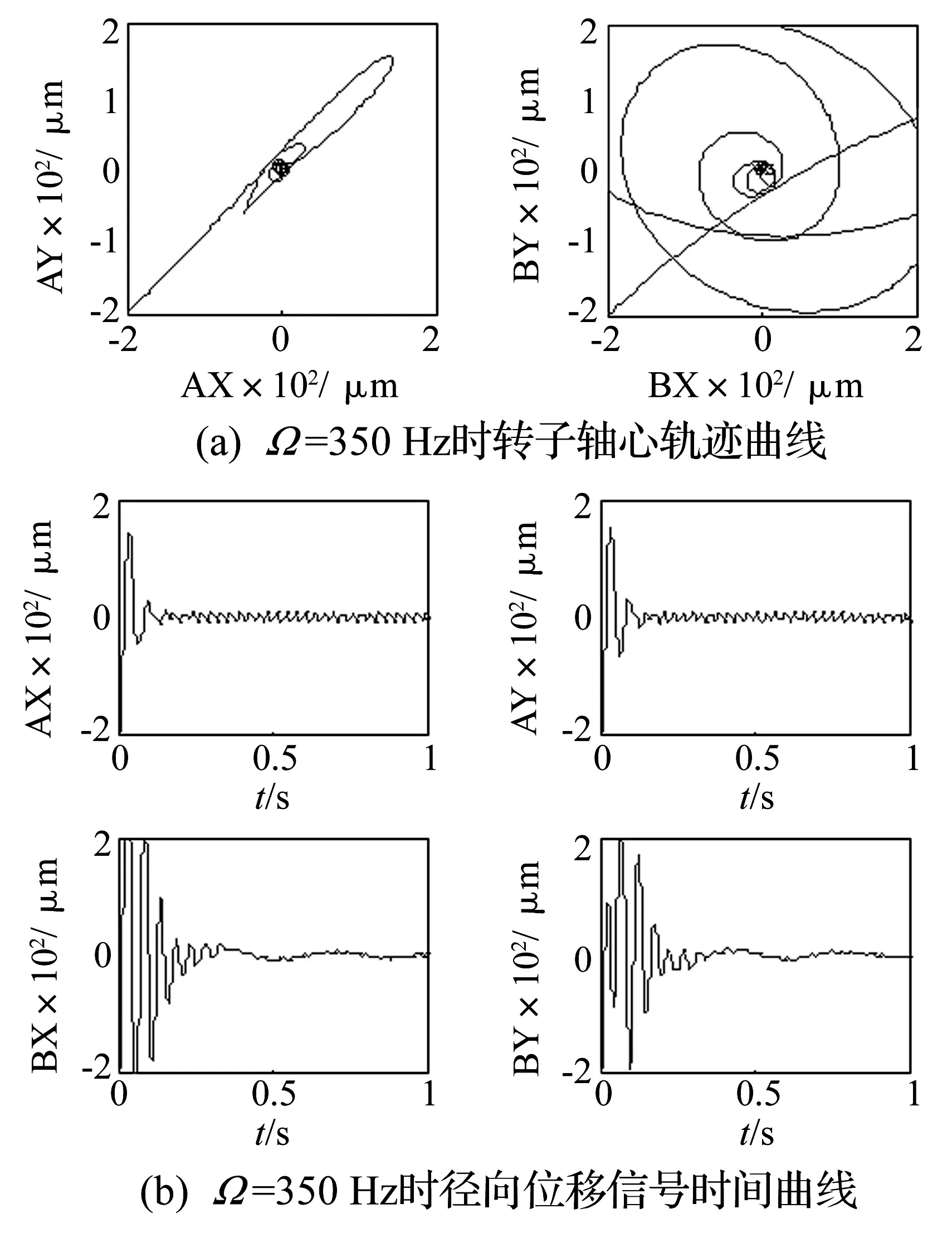
图9 Ω=135 Hz时转子运动状态Fig.9 The kinstate of the axis when Ω=350 Hz

5 全转速范围内非对称转子陀螺效应抑制实验

利用北京航空航天大学研制的高真空大抽速磁悬浮复合分子泵的偏心大惯量刚性高速磁悬浮转子系统进行了考查转速自适应的多通道单边滤波PIDC方法陀螺效应抑制效果的实验。其主要技术参数如表1和表2所示。实验时转子从0 Hz时开始升速，同时用示波器记录径向四通道AX、AY、BX和BY位移信号和频谱。磁轴承控制系统采用TMS320F28335+FPGA数字控制系统，并采用转速自适应的多通道单边滤波PIDC控制方法，对分子泵进行升速稳定性测试。实验平台如图10所示。

图10 陀螺效应抑制实验平台Fig.10 Experimental platform of suppression of gyroscopic effect

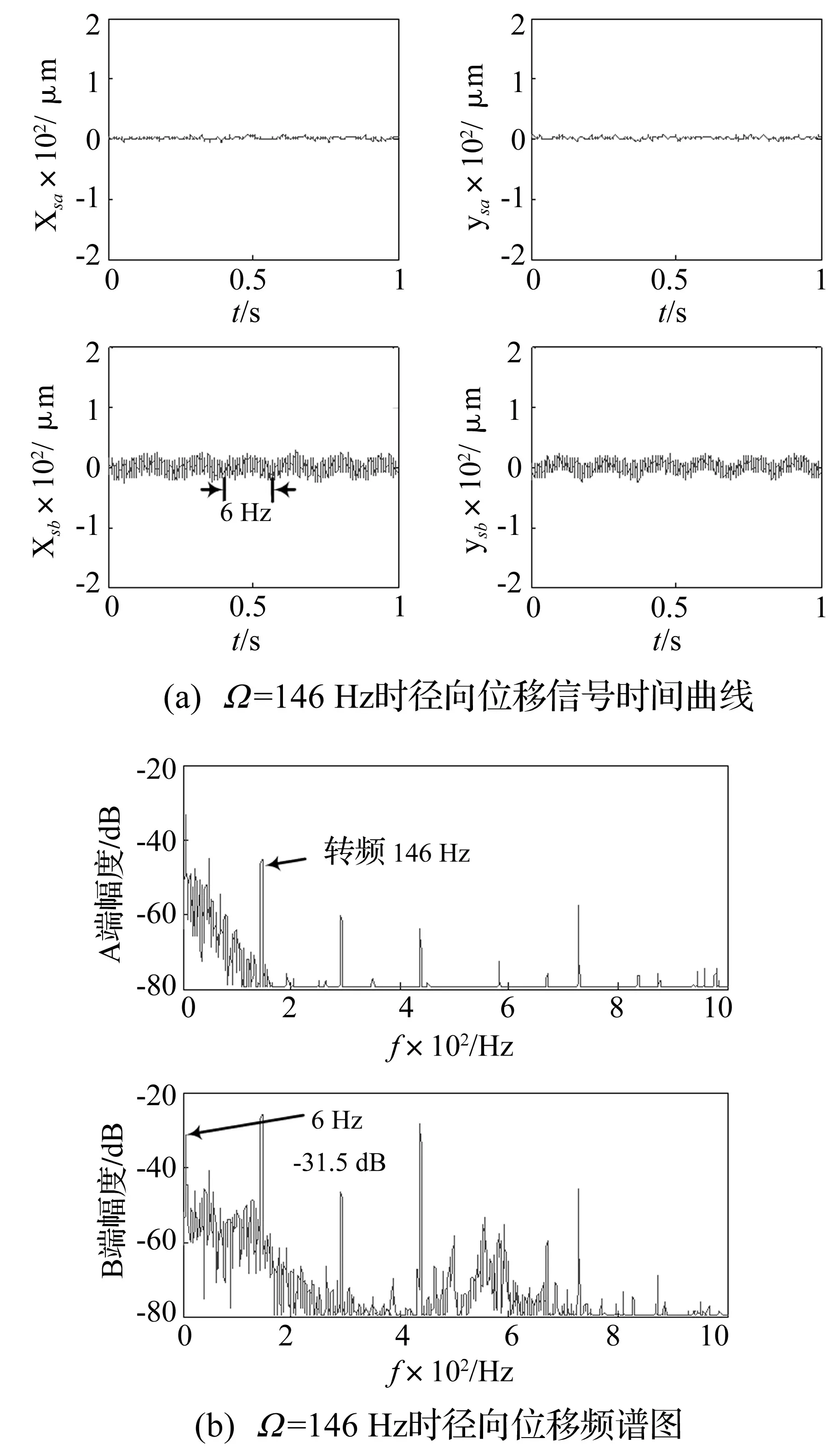
图11 Ω=146 Hz时转子运动状态Fig.11 The kinstate of the axis when Ω=146 Hz

当转频升至146 Hz时，B端出现了一个频率6 Hz，幅值-31.5 dB的低频扰动(见图11(a)、图11(b))，且其频率随转速升高而降低，加入交叉比例kc=0.8和仿真时预调的CLPF参数值，但抑制程度有限，将CLPF增益kL的值改为0.96，该扰动得到有效的抑制，这说明此低频扰动为进动失稳频率，且仿真预调结果与实验所需参数值稍有出入但变化不大，与仿真结果基本相符。

继续将转频升至166 Hz，在B端同频附近出现一个频率145 Hz，幅值-32.6 dB的高频扰动(见图12(a)、图12(b))，并且其频率随转速继续升高，根据转子运行时章动频率与转频的比例关系推知此扰动可能为章动，加入CHPF预调参数并做适当修改后，系统趋于稳定。

图12 Ω=166 Hz时转子运动状态Fig.12 The kinstate of the axis when Ω=166 Hz

在以上仿真分析预调参数的基础上，通过全转速测试中对CHPF各通道预调参数的优化改进，将分子泵复合转子转速离散成5个转速段，CHPF通道采用5级切换，具体控制参数如表3所示。

表3 转速自适应的多通道单边滤波交叉反馈控制参数Tab.3 The parameters of speed-adaptive multi-channel unilateral filtering PIDC control method

最终分子泵复合转子稳定运转到最高设计转速21 000 r/min(见图13(b))，由图13(a)可以看出此时A端振幅为23.4 μm，B端振幅为16 μm，均未达到保护间隙的1/8，由于加入PIDC控制方法，额定转速下B端跳动量反而要优于A端，实现了额定转速下系统的稳定运行。

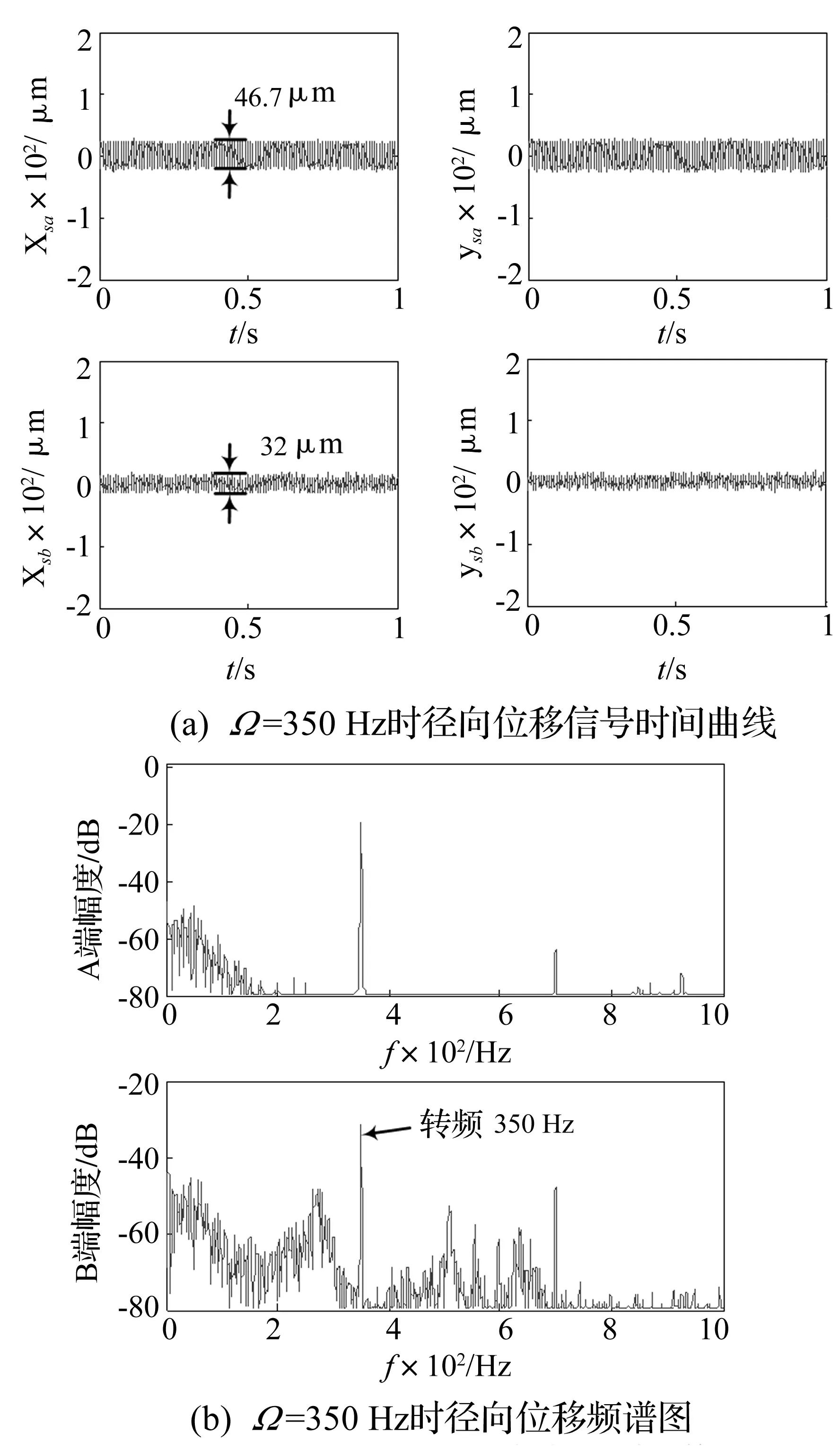
图13 Ω=350 Hz时转子运动状态Fig.13 The kinstate of the axis when Ω=350 Hz

6 结 论

对于非对称大惯量刚性转子不同于一般对称转子的特性，本文建立了基于陀螺技术方程的磁轴承-非对称转子动力学模型，并对非对称转子高速运转时质心远端单独出现的涡动模态失稳的现象提出了一种转速自适应的多通道单边滤波PIDC控制方法，由此建立的仿真模型为控制系统设计CLPF和CHPF通道控制参数提供了理论指导，实验中进而不断对仿真预调参数进行优化与改进，最终通过CLPF通道与CHPF的5级通道自动切换完成了对分子泵复合转子的全转速陀螺效应抑制，使分子泵样机能够稳定运行在额定转速下。

由于实际被控对象参数的限制，在仿真和实验过程中始终未出现A端涡动模态失稳，那么A端是否和B端一样也存在临界转速值，而B端轴承加入抑制算法后是否会对A端涡动模态产生影响，这些问题有待进一步深入研究。

[1] CHEN S L, WENG C C. Robust control of a voltage-controlled three-pole active magnetic bearing system[J]. IEEE/ASME Transactions on Mechatronics, 2010, 15(3): 381-388.

[2] 朱熀秋, 曾润章. 交流磁轴承技术研究进展[J]. 电机与控制应用, 2014, 41(9): 45-50. ZHU Huangqiu, ZENG Runzhang. Advances in AC magnetic bearing technology[J]. Electric Machines & Control Application, 2014, 41(9): 45-50.

[3] NOH M D, CHO S R, KYUNG J H, et al. Design and implementation of a fault-tolerant magnetic bearing system for turbo-molecular vacuum pump[J]. IEEE/ASME Transactions on Mechatronics, 2005, 10(6): 626-631.

[4] 韩放. 叶片—转子系统振动特性与参数辨识方法研究[D]. 大连：大连理工大学, 2013.

[5] WANG L, CAO D Q, HUANG W. Nonlinear coupled dynamics of flexible blade-rotor-bearing systems[J]. Tribology International, 2010, 43(4): 759-778.

[6] BLUSSEAU P, PATEL M H. Gyroscopic effects on a large vertical axis wind turbine mounted on a floating structure[J]. Renewable Energy, 2012, 46(5):31-42.

[7] 夏元清, 付梦印, 邓志红,等. 滑模控制和自抗扰控制的研究进展[J]. 控制理论与应用, 2013, 30(2):137-147. XIA Yuanqing, FU Mengyin, DENG Zhihong, et al. Recent developments in sliding mode control and active disturbance rejection control[J]. Control Theory & Applications, 2013, 30(2):137-147.

[8] WEN X L, SONG C S, CAO C, et al. Study of the LQR controller for magnetic flywheel rotor system[C]// Applied Mechanics and Materials. 2012, 150: 221-226.

[9] LIU L, ZHANG G S. State and output control for linear systems based on eigenstructure assignment[J]. Journal of Tianjin University of Technology, 2013,29(6):12-16.

[10] NOSHADI A, SHI J, LEE W S, et al. High performanceH∞control of non-minimum phase active magnetic bearing system[C]//Industrial Electronics Society, IECON 2014-40th Annual Conference of the IEEE.Piscataway:IEEE, 2014:183-189.

[11] 陆豪, 李运华, 田胜利, 等. 驱动大惯量低刚度负载的推力矢量控制电动伺服机构的μ综合鲁棒控制[J]. 机械工程学报, 2011, 47(2): 180-188. LU Hao, LI Yunhua, TIAN Shengli, et al.μsynthesis robust control of thrust vector control electric servo mechanism driving large inertia and low stiffness[J]. Journal of Mechanical Engineering, 2011, 47(2): 180-188.

[12] CHEN Y, DAVIS T A, HAGER W W, et al. Algorithm 887: CHOLMOD, supernodal sparse cholesky factorization and update/downdate[J]. Acm Transactions on Mathematical Software, 2008, 35(3):1-14.

[13] FAN Y H, FANG J C. Experimental research on the nutational stability of magnetically suspended momentum flywheel in control moment gyroscope (CMG)[C]// 9th International Symposium on Magnetic Bearings. Kentucky,2004: 3-6.

[14] CHEN X, CHEN M. Precise control of a magnetically suspended double-gimbal control moment gyroscope using differential geometry decoupling method[J]. Chinese Journal of Aeronautics, 2013, 26(4):1017-1028.

[15] TONG W, JIANCHENG F. A feedback linearization control for the nonlinear 5-DOF flywheel suspended by the permanent magnet biased hybrid magnetic bearings[J]. Acta Astronautica, 2012, 79(10): 131-139.[16] 张剀，赵雷，赵鸿宾. 电磁力超前控制在磁悬浮飞轮中的应用[J]. 机械工程学报，2004，40(7)：175-179. ZHANG Kai, ZHAO Lei, ZHAO Hongbin. Application of magnetic force lead control on a flywheel suspended by AMBS[J]. Journal of Mechanical Engineering, 2004, 40(7): 175-179.

[17] AHRENS M, KUCERA L. Cross feedback control of a magnetic bearing system: controller design considering gyroscopic effects[C]// In Eidgenoessische Technische Hochschule, Third International Symposium on Magnetic Suspension Technology.1996: N96-35897,12-18.

[18] WANG L, CAO D Q, HUANG W. Nonlinear coupled dynamics of flexible blade-rotor-bearing systems[J]. Tribology International, 2010, 43(4): 759-778.

[19] GENTA G. On the stability of rotating blade arrays[J]. Journal of Sound and Vibration, 2004, 273(4): 805-836.

Adaptive suppression of the gyroscopic effect of rigid asymmetric magnetically suspended high-speed rotor with large inertia

SHEN Yifei1,2, HAN Bangcheng1,2, ZHENG Shiqiang1,2

(1. Science and Technology on Inertial Laboratory, Beihang University, Beijing 100191, China;2. Fundamental Science on Novel Inertial Instrument & Navigation System Technology Laboratory, Beihang University, Beijing 100191, China;3. High Speed Magnetic Levitation Motor Technology and Application Engineering Technology, Research Center, Beihang University, Beijing 100191, China)

A dynamic model for rigid asymmetric rotors was established for investigating the vortex mode instability of a high speed unilateral rigid rotor with large inertia under rigid asymmetric magnetic suspensions. Meanwhile, a speed-adaptive multi-channel unilateral filtering PIDC control method was presented, which can compensate the phase of the instability of vortex motion at the end away from the rotor centroid by switching over feedback channels automatically for different rotational speed to optimize the preset parameters. The simulation results show that this easily-used method of PIDC control can effectively resolve the instability of precession and nutation modes at one end of the rotor which is caused by gyroscopic effect of the rotor at high speed. Experiments verify the reliability of the method: the prototype of a molecular pump can smoothly achieve the design specification of vacuum performance, when the speed is increased to 21 000 r/min.

asymmetric; gyroscopic effect; speed-adaptive; multi-channel unilateral filter; PIDC control

国家自然科学基金资助项目(61203203)；国家重大科学仪器设备开发专项(2012YQ040235)；北京市科技创新基地培育与发展工程专项项目(J131104002813105)

2015-06-15 修改稿收到日期：2015-10-07

沈易霏 男，硕士生，1988年10月生

韩邦成 男，博士，研究员，1974年2月生

TP273+.2

A

10.13465/j.cnki.jvs.2016.22.012