大数据条件下网络零售商的经济批量问题*

刘艳秋，裴艳霞，蔡 超

（沈阳工业大学a.理学院，b.管理学院，沈阳 110870）

大数据条件下网络零售商的经济批量问题*

刘艳秋a，裴艳霞a，蔡 超b

（沈阳工业大学a.理学院，b.管理学院，沈阳 110870）

为了研究一个有限计划期内，在供应商处于大数据的条件下，网络零售商满足客户个性化需求的补货及发货批量策略制定问题，对大数据进行预处理，筛选有效的客户浏览行为，通过信息过滤，优选服务供应商.由于建立的批量问题模型具有一定的复杂性，设计多项式算法求解批量模型，从而获得问题的最优解，选择最终供应商及制定批量策略.结果表明，该处理方法具有一定的有效性，为大数据条件下网络零售商满足客户个性化、定制化需求的经济批量问题提供了解决方法.

大数据；个性化需求；定制化需求；网络零售商；内容过滤；用户浏览行为；经济批量；动态规划

随着互联网的普及，零售商不再局限于地域的限制，而是呈现虚拟化、网络化的特点.互联网上零售商面向客户的服务越来越趋于个性化、定制化模式，大数据时代的来临，标志着对上述问题的传统数据处理方式已经无法满足人们对数据的要求［1－2］.经济全球化使得供应链中各成员之间的竞争日益激烈，在激烈的市场竞争中提升企业竞争力是关键，如何提高企业利润至关重要.自从Wagner和Whitin首次提出经济批量问题（economic lot-sizing）以来，该问题就成为企业利润管理中的一个重要的研究课题.

目前，国内外已出现不少对批量问题的研究，主要集中在供应商选择研究和客户研究上.例如，Sandra［3］综合考虑了选择供应商及运输方式环境下的采购批量问题，并设计了多项式时间算法求解；徐健腾等［4－5］首先在供应商不同数量折扣的条件下，研究了基于多供应商和多零售商构成的经济批量问题；汪小京等［6］研究了供应商管理库存时，一个供应商和一个带时间窗需求的顾客情况下，供应商库存补货及发货批量问题；吕文元等［7］研究了考虑设备故障的经济生产批量模型，在得到经济生产批量的同时求解最优设备检查策略.在零售商与顾客之间的销售中，柳健［8］提出了零售企业处于不同的库存形态时不同经济订货批量策略；刘艳秋等［9］提出了优惠券促销定价模型，提高了销售中的优惠券使用率；罗兵等［10］研究了销售过程中特价商品处于价格和存货影响需求的条件下，零售商对其经济订货批量的模型.但总体上，对大数据下零售商的供应商选择和对客户个性化需求还需要进一步研究.

1 模型构建

1.1 零售商经济批量问题描述

通常零售商经济批量问题可描述为：零售商在某时期内订购产品，已知时期内顾客的需求量、产品的单位库存费用及进货费用，且这些参数随着时期的变化而变化.问题的目标是制定最优补货和发货决策，降低零售商自身的总成本，实现其利润最大化.

大数据情况下，零售商的经济批量问题更多地需要确定时期内海量供应商的选择，优化目标在降低零售商销售前成本的同时兼顾客户的个性化需求.

1.2 符号说明

基于问题的建模需要，假设在一个包含h个周期、周期时长均为T的计划期H内，零售商面向供应商群体订购某种产品，已知供应商不同时期对产品的单位订购成本及数量折扣.经大数据处理后，供应商优选的数目为M个，要满足N（N≥2）个客户的个性化需求，顾客的时间窗需求已知.假设供应商供应能力、零售商运输能力和库存容量均无约束.

令客户i的需求为di，时间窗为｛ei，li｝，已知零售商与供应商j之间的距离为Dj，零售商与客户i之间的距离为Si，以及运送货物车辆的车速为v.符号定义如下：Ti为零售商的产品实际送达到顾客i的时间；It为第t期末零售商仓库的库存水平；ht为第t期内零售商仓库的单位库存成本；cjt为第t期内在供应商j处的单位订购价格；rjt为第t期内在供应商j处订货的折扣率，当订购量在区间［di，di＋1）时，折扣率为rjμt；djμ为折扣节点处订货量，μ＝0，1，2，…，η；djt为在供应商j处的订货量.

数量折扣函数表达式为

式中，Cjt为在供应商j处订货费用.

1.3 零售商批量成本模型

零售商在计划期内的总成本应包括4个部分，分别如下所示.

1）价格成本f1（x，y），其表达式为

2）运输成本f2（x，y），其表达式为

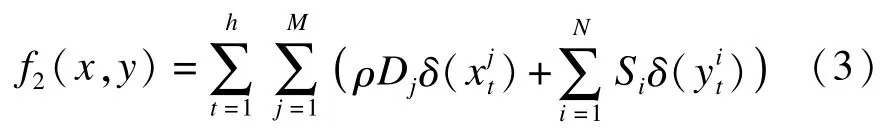
式中：ρ为零售商补货发货的单位运输成本；yit为第t期内给客户i的发货批量，t＝1，2，…，h.

3）库存成本g（x，y），其表达式为

4）时间惩罚成本 h（x，y），其表达式为

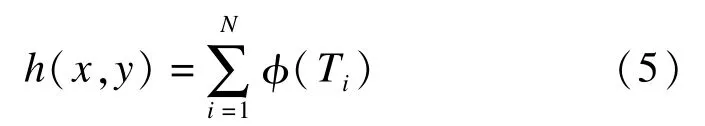
式中，φ（Ti）为惩罚函数，且

其中，α、β均为惩罚系数，ei、li分别为顾客i规定到达的最早、最晚时间.

计划期内的网络零售商批量成本数学模型为

式（7）表示零售商各时期的库存平衡，式（8）表示零售商初始库存I0和计划期末库存 IT为零，式（9）表示惩罚成本限制为ε，式（10）、（11）表示每个时期的补货及发货批量约束条件，式（12）表示每个时期末零售商库存水平不小于零.

2 数据预处理

2.1 数据预处理设计

通常零售商对供应商进行选择，通过考虑商品成本、产品质量和服务质量等多个因素的影响来实现选择，如1996年Dickson的研究提出了供应商选择评价准则来选择供应商.供应商及客户数据较多时，零售商的进货选择经常需要受到供应商的规模、相互关联性和客户偏好等因素的影响，选择往往比较困难.

针对研究数据，文中设计了以下 3个处理过程：1）对供应商数据细分到每个客户；2）对每个客户的数据信息进行处理，得到对应能满足该客户个性化需求的供应商集合；3）合并所有客户对应信息，根据批量成本模型计算零售商最小成本批量.

2.2 预处理的具体步骤

零售商的获利关键在于客户的兴趣度，客户对网售商品的点击浏览率成为零售商对供应商选择的重要度量.数据处理的核心问题是客户对应的供应商信息过滤，文献中常见的信息过滤方式有内容过滤和协作过滤两种.

问题中的供应商数据量较大，用户评分不易得到，通过协作过滤的方式不易处理.浏览的网页信息数据不仅包含文本内容，还包含如图片等难以用数学指标描述的信息，传统的内容过滤方式在处理文本数据上有显著效果，但网页内其他信息不能反映.针对问题中的数据特点，基于客户行为改进个性化推荐算法，首先根据客户浏览的网页特点，定义客户兴趣度，然后使用空间向量模型（VSM模型）表示客户兴趣及供应商兴趣，最后基于客户特殊标记行为，改进客户兴趣向量后，由相似度计算方法给出推荐度最大的供应商集合.

2.2.1 客户兴趣度

客户兴趣反映了客户消费行为的倾向性，客户兴趣度大的商品易受到客户喜爱.零售商在提供产品时，如能提供客户兴趣度大的产品，能提高客户满意度.对客户的兴趣，通过分析客户浏览行为获取，如对网页的操作（收藏或另存为、复制和保存）和对网页的浏览时间等.

客户在对产品浏览时产生的信息数据不仅仅是文本信息，还包括各种图片信息，不能仅以浏览时间和字符数目定义客户兴趣度.本文以客户浏览速度为标准，定义客户兴趣度.

设i为一个客户，u为商品页面，定义客户浏览速度为

式中：θui表示客户对页面的浏览时间；size（u）表示页面的大小.

客户兴趣度为

式中：Dui＝1表示客户对页面进行了收藏或另存为、复制和保存；δ1和δ2分别表示客户浏览网页时间过短或过长的情况.

2.2.2 客户兴趣向量

关键词的权重常采用TFIDF算法，随着关键词的权重在文件中出现的次数正比增加，在文档库出现的频率却反比下降，其表达式为

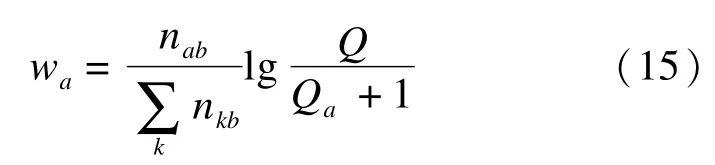
式中：wa为关键词 a的权重；nab为a在文件 b中的出现次数为文件b中所有字词数；Q为文档总数；Qa为包含关键词 a的文件数.

2.2.3 相似度计算

兴趣的相似度计算采用余弦相似度计算，但为了防止关键词的漏选，预先进行关键词合并.设空间向量模型中给出供应商j的关键词向量为vj＝（t1，t2，…，tn），t为关键词，共有 n个；客户 i的空间向量模型的关键词向量为vi＝（t1，t2，…，tm），t为关键词，共有m个；客户i有标记关键词向量为vi*＝（t1，t2，…，tr），t为关键词，共有 r个.合并向量 vij＝vi∪vj∪vi*，合 并后 的向 量中 关 键词的个数为k，且max（m，n，r）≤k≤m＋n＋r.对比合并后的向量 vij，原供应商关键词向量vj、客户关键词向量vi及标记关键词向量 vi*均可改写为1×k向量.

对有客户标记的关键词，只用TFIDF算法计算权重显然不合理.对客户标记关键词向量），对应权重向量作归一化处理后为，原客户关键词权重向量为，结合两者作为客户新的权重向量，即，其中，q为比例系数，表示网络零售商对客户标记和网页推荐的偏重程度，本文取

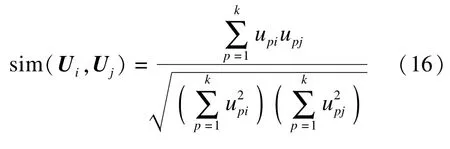
3 模型求解算法设计

设阶段数为G，则有

在拉丁舞中双人的配合更多的是通过手部来连接，而面部表情是舞伴之间情感交流的另一重要方式，同时也是舞者与观众之间信息传达的重要方式之一，表情不是刻意为之而是与动作和情绪紧密相连的，表情的丰富才使得舞蹈更加多彩。

若给定所有的C（g，h），则零售商最小总成本均可在 O（G2）时间内求出.

设在本文问题建立的模型中客户i的供应商集合为Ai，1≤i≤N.若所有客户供应商集合均不相同，即对客户，则C（g，h）可表示为

为了求解所有的C（g，h），可先求解 Ci（g，h）.为了求解满足客户i在 g－1到 h期满足需求所需的最小总成本，采用最短路径算法，可先求解客户在g－1到 h期满足需求经过的最短路径.

模型的求解过程如下：

1）根据零售商的客户i信息数据，做数据预处理，得到对应的供应商推荐集 Ai.

3）用Dijkstra算法计算满足单个客户需求的最短路径，求解最小成本Ci（g，h），代入式（18）求解最小总成本C（g，h），转5）.

4）用Dijkstra算法计算满足联合客户需求的的最短路径，求解最小成本 Ci（g，h），代入式（19）求解最小总成本C（g，h），转5）.

5）代入所有的C（g，h），求解最小总成本F（h），确定满足最小总成本的最短路径时的最优决策.

4 数据仿真

4.1 优选供应商

已知零售商的客户信息（包括浏览信息及标记信息等），按照上述数据预处理的算法流程，计算客户兴趣度，得到有效页面数据，然后通过TFIDF算法计算客户及供应商关键词及其权重，合并客户标记关键词向量，最后计算客户和供应商之间的相似度，优选出作为客户的最终可选择的供应商集合.为了模型求解的需要，随机选择零售商数据库中的一个客户，其浏览过的供应商总量为3 256，根据浏览信息代入式（13）、（14）进行计算，得到有效供应商页面为3 150，通过TFIDF算法及标记关键词合并计算，计算结果代入式（16），可计算客户与各供应商之间的相似度，最终优选出推荐度最大的3个供应商作为备选供应商集合.

4.2 零售商批量问题仿真

任意选择 4个客户对其服务，考虑计划期H＝8 d，产品运送速度v＝300 km／d，单位运送成本ρ＝0.5元／kg，单位库存成本不变，h＝0.1元／kg，惩罚系数α＝200元／d，β＝300元／d，客户与零售商之间的距离分别为120、50、100和450 km.用上述优选供应商的方法，得到客户1的推荐供应商1、2、3的折扣函数信息为

客户2的推荐供应商4、5、6的折扣函数信息为

客户3的推荐供应商7、8、9的折扣函数信息为

客户4的推荐供应商 10、11、12的折扣函数信息为

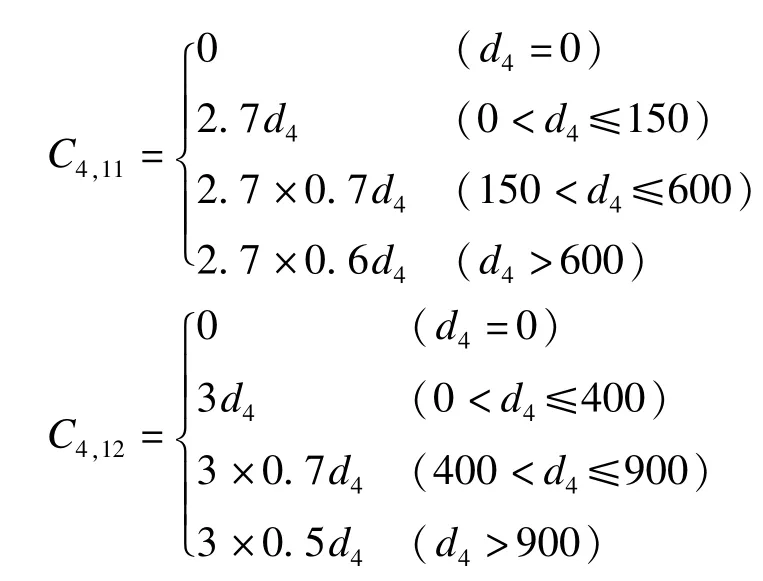
以上订货量均以kg为单位，供应商与零售商及客户之间的各种数据如表1～2所示.

表1 客户时间窗需求Tab.1 Time w indow demand of customers

表2 供应商距离参数与固定成本Tab.2 Distance parameter of supplier and fixed cost

根据上述供应商及客户数据代入模型，利用Dijkstra算法求解出客户所有的C（g，h），代入式（18）求解出对应的最小总成本，从而确定零售商对客户的最优补货及发货策略.最终解出零售商的最小成本为5 850.75元，选择的供应商及补货发货时期决策如表3所示.

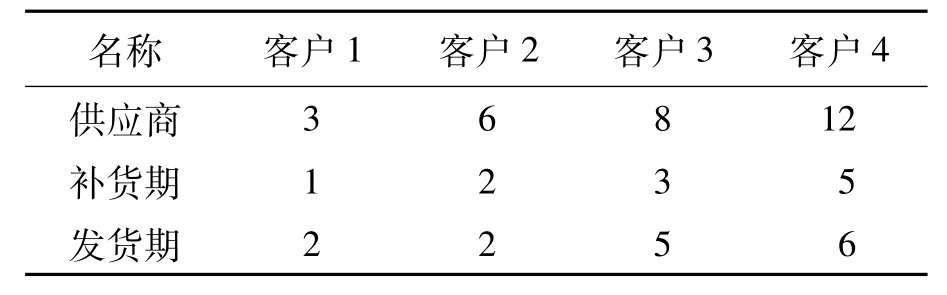
表3 各时期选择的供应商及补货发货决策Tab.3 Selected suppliers as well as replenishment and delivery decision in each period

在求解过程中可以发现，满足客户1的需求时，采用供应商1的单位订购价格及折扣率能使得价格成本更小，但由于时间窗的约束，使得最优成本选择为供应商 3，并且由于晚于规定时间窗送达，计算成本中包含惩罚函数成本；由于第3期在供应商8处补货，产生的总成本比早于或晚于时间窗的补货发货总成本小，因此对客户 3选择在第3期补货，并选择承担一部分库存成本；客户4的供应商有与客户 1相同的供应商，但是由于成本的限制，优选其他供应商对其服务.

最终结果满足客户的实际时间窗需求，由于供应商数据是基于对客户的个性化推荐得到的，也能满足客户的个性化需求.在解决网络零售批量问题的基础上，满足客户的个性化需求.

5 结 论

本文研究了大数据环境下有限计划期内，网络零售商补货及发货批量问题.由于数据具有大量多样的特点，利用改进的基于内容过滤的个性化推荐算法处理供应商数据，满足客户个性化需求，建立批量问题模型，设计算法求解，满足客户时间窗需求.采用先进的信息处理方法，能够满足顾客越来越个性化、定制化的消费需求，为网络零售商提供一种解决批量问题的方法.

（

）：

［1］王元卓，靳小龙，程学旗.网络大数据：现状与展望［J］.计算机学报，2013，36（6）：1125－1138.（WANG Yuan-zhuo，JIN Xiao-long，CHENG Xue-qi. Network big data：present and future［J］.Chinese Journal of Computers，2013，36（6）：1125－1138.）

［2］孟小峰，慈祥.大数据管理：概念、技术与挑战［J］.计算机研究与发展，2013，50（1）：146－169.（MENG Xiao-feng，CIXiang.Bia data management：concepts，techniques and challenges［J］.Journal of Computer Research and Development，2013，50（1）：146－169.）

［3］Sandra D E.A primal-dual algorithm for the economic lot-sizing problem with multi-mode replenishment［J］.European Journal of Operational Research，2009，197：93－101.

［4］徐健腾，张玉忠，柏庆国.多供应商多零售商经济批量问题的多项式时间算法研究［J］.运筹学学报，2011，15（4）：102－114.（XU Jian-teng，ZHANG Yu-zhong，BAI Qing-guo.A polynominal time algorithm for the economic lot-size problem with multiple suppliers and multiple retailers［J］.Operations Research Transactions，2011，15（4）：102－114.）

［5］Bai Q G，Xu JT，Zhang Y Z，et al.An optimal solution for economic production quantity models with deteriorating items and time-varying production cost［J］.Operations Research Transactions，2013，17（4）：109－122.

［6］汪小京，刘志学，刘丹.时间窗需求下供应商管理库存补货及发货动态批量研究［J］.计算机集成制造系统，2010，16（7）：1505－1514.（WANG Xiao-jing，LIU Zhi-xue，LIU Dan.Dynamic lot-sizing policy of replenishiment and dispatch in the VMI supply chain with time window demand［J］. Computer Integrated Manufacturing Systems，2010，16（7）：1505－1514.）

［7］吕文元，化彬.考虑设备故障维修时间的经济生产批量模型［J］.计算机集成制造系统，2015，21（5）：1309－1314.（LÜWen-yuan，HUA Bin.EMQ models with random repair time of machine failure［J］.Computer Integrated Manufacturing Systems，2015，21（5）：1309－1314.）

［8］柳健.基于零售业不同库存形态的经济订货批量策略［J］.物流技术，2012，31（2）：132－134.（LIU Jian.EOQ strategy for different inventory practices of retail industry［J］.Logistics Technology，2012，31（2）：132－134.）

［9］刘艳秋，谢萌，丁伟祥.基于RCEPN的资源配置优化模型与方法［J］.沈阳工业大学学报，2013，35（6）：667－671.（LIU Yan-qiu，XIE Meng，DING Wei-xiang.Optimization model and method for resource configuration based on RCEPN［J］.Journal of Shenyang University of Technology，2013，35（6）：667－671.）

［10］罗兵，冯璐，陈星岐.交叉销售下价格和存货影响需求的特价商品经济订货批量模型［J］.系统工程理论与实践，2014，34（4）：826－835.（LUO Bing，FENG Lu，CHEN Xing-qi.Econom ic order quantity model for off-price merchandise with demand depends on selling price and tock under crossselling［J］.Systems Engineering：Theory＆Practice，2014，34（4）：826－835.）

（责任编辑：钟 媛 英文审校：尹淑英）

Economic lot-sizing problem of on line retailer under condition of big data

LIU Yan-qiua，PEIYan-xiaa，CAI Chaob
（a.School of Science，b.School of Management，Shenyang University of Technology，Shenyang 110870，China）

In order to study the establishment problem of replenishment and delivery lot-sizing strategy for on line retailers in satisfying the personalized customer demands within a finite planning period when the suppliers are under the condition of big data，the big data were preprocessed，the effective customer browsing behavior was screened，and the service suppliers were optimized and selected through information filtering.Due to the complexity of the established lot-sizing problem model，a polynomial algorithm was designed to solve the lot-sizing model，and the optimal solution of the problem was obtained.In addition，the final supplier was selected，and the lot-sizing strategy was established.The results show that the proposed method has certain effectiveness，and can provide the solution for the economic lot-sizing problem of on line retailer in satisfying the personalized and customized demands of customers under the condition of big data.

big data；personalized demand；customized demand；on line retailer；content filtering；user browsing behavior；economic lot-sizing；dynamic planning

TF 272.1

A

1000－1646（2016）06－0651－06

10.7688／j.issn.1000－1646.2016.06.10

2015－11－09.

辽宁省科学技术计划基金资助项目（2013216015）；沈阳市科学技术计划基金资助项目（F14－231－1－24）.

刘艳秋（1963－），男，吉林四平人，教授，博士生导师，主要从事复杂系统可靠性建模与优化等方面的研究.

09－07 16∶08在中国知网优先数字出版.

http：∥www.cnki.net／kcms／detail／21.1189.T. 20160907.1608.032.htm l