改进PSO-BPNN的电力变压器故障诊断与模式识别*
夏琳琳,文 磊,刘惠敏,初 妍,台金娟(.东北电力大学自动化工程学院,吉林吉林 0;.青岛农业大学 机电工程学院,山东 青岛 6609;.哈尔滨工程大学 计算机科学与技术学院,哈尔滨5000)
改进PSO-BPNN的电力变压器故障诊断与模式识别*
夏琳琳1,文 磊1,刘惠敏2,初 妍3,台金娟1
(1.东北电力大学自动化工程学院,吉林吉林 132012;2.青岛农业大学 机电工程学院,山东 青岛 266109;3.哈尔滨工程大学 计算机科学与技术学院,哈尔滨150001)
为了优化反向传播网络相关学习参数,提出一种粒子群优化辅助 BP神经网络(BPNN)的新方法.以变压器油中气体体积分数百分比构造故障特征,将 BP网络的初始权值和阈值进行实数编码,以对应PSO中的粒子,实现 BP网络的离线训练与在线分析,对变压器故障模式做出判断.结果表明,该算法更合理地更新了粒子的位置和速度,最优地设置了全局极值,有效克服了粒子的早熟收敛,获得的故障诊断准确率高达91%,并大大提升了 BP网络的收敛速度.该算法为此类设计提供了有效的模型参考.
粒子群优化算法;混沌初始化;惯性权重;高斯扩张变异;BPNN方法;电力变压器;故障诊断
变压器是重要的电力设备,检测、诊断并及早排除其可能存在的故障与整个电力系统的安全性、经济性休戚相关.油中溶解气体分析法(dissolved gas analysis,DGA)是应用最为广泛的变压器故障诊断方法[1],其主要通过油中溶解气体的组分和含量与变压器故障类型间的对应关系进行模式分类与故障诊断.然而,油中气体成分及含量呈高度非线性,难以用精确数学模型进行描述.
BP神经网络是通用的非线性万能逼近器,即选择足够多的隐层数和隐层节点数,可逼近任意非线性函数到任意精度.将其与DGA技术相结合,能够在一定程度上代替在线分析仪表,实现故障模式的诊断与识别.BP算法隐层多使用Sigmoid或双曲正切函数进行激活,其值在输入空间无限大的范围内为非零值,使得其实现非线性逼近的机理为全局逼近模式,收敛速度有所拖慢.粒子群优化(PSO)作为一种最优化计算方法,在确保全局搜索能力、高效的启发式搜索模式同时,又能有效提升算法的收敛速度[2-3],使得由其辅助BP网络优化相关参数的学习成为可能.
1 标准PSO算法
同遗传算法、蚁群算法及差分进化算法等智能优化算法相类似,PSO也是通过模拟揭示自然现象和过程来实现的,其主旨是通过群体中个体间的协作实现最优解的搜寻.具体地,将优化问题的每个可行解都看作搜索空间中的一个粒子,优化函数决定粒子的适应度值,速度向量决定粒子的前进方向和距离.在针对具体问题的实际应用中,首先需初始化一群随机粒子,在每次迭代搜索过程中,粒子通过两个极值(pid,pgd)的不断更新,并施以一定代数的迭代直至找到问题的最优解.其中,pid为粒子本身迄今找到的最优解,即个体极值,pgd为整个种群迄今找到的最优解,即全局极值.
粒子的速度、位置更新公式[4-5]表示为

式中:vkid+1和xkid+1分别为第i个粒子在 k+1次迭代中第d维的速度和位置,粒子每一维的最大速度和坐标都被限制在允许范围内;c1和c2为学习因子,通常 c1=c2=2;r1和r2为[0,1]的随机数;ω为惯性权重,用于实现算法全局搜索和局部搜索间的平衡,ω的取值一般在0.4~0.9之间.
2 PSO改进模型
标准 PSO存在早熟收敛、易陷入局部极值等问题,表现为:经过相当步数的迭代后,某些特征会呈现相对优势的状态,且进程中这样的特征不会再有很大的变化.为了打破群内的平衡态以期达到更高的平衡态,就需要算法跳出局部最优.以下从初始化策略分析、惯性权重项调整及全局极值高斯扩张等对PSO优化算法进行分析、改进,并实现三种改进模式的融合.
2.1 混沌初始化策略
混沌序列具有较好的随机性和遍历性,能在一定的范围内按其自身规律不重复地遍历所有状态.借助上述特性,对粒子群中粒子进行混沌初始化,可保持初始群体随机性和提高种群多样性,使初始群体均匀分布在优化问题的寻优空间中.通过对多种混沌映射方法仿真对比发现,Logistics混沌映射在全局迭代次数不是很大时,具有相对最均匀的数值分布,其数学模型[6]可表示为

式中,r为混沌吸引子,当r=4时,系统处于完全混沌状态,此时zn+1∈(0,1).
图1分别给出了当随机数个数为30、50时,随机初始化和Logistics混沌映射初始化随机数分布,两种情况下 Logistics混沌映射的均匀程度均好于随机映射,且每迭代一次产生一次随机数,故当随机数为50时,Logistics混沌映射更加均匀.

图1 初始化随机数分布Fig.1 Distribution of initialized random number
2.2 惯性权重的调整
惯性权重ω是PSO算法中重要的可调参数,它决定了粒子前一时刻飞行速度对当前时刻飞行速度的影响.Shi和Eberhart在文献[7]中证明了:ω较大时算法全局搜索能力强,ω较小时算法局部搜索能力强.本文给出一种 ω呈指数规律变化的策略,以改善常用方法下,惯性权重线性递减策略对复杂、非线性搜索过程的调节能力有限的局限[8-9],调整公式为
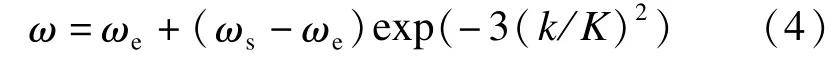
式中:ωs、ωe分别为ω的初值和终值;k为当前迭代次数;K为最大迭代次数.该策略确保了在算法迭代前期 ω具有较大的值且缓慢减小,有利于全局搜索;在算法迭代后期,ω具有较小的值,有利于局部搜索.
图2给出了当ωs=0.9、ωe=0.4、K=1 000时的惯性权重变化,其中线性变化曲线按ω=ωs+(ωe-ωs)(k/K)函数关系获得.

图2 惯性权重随迭代次数的变化曲线Fig.2 Change curves for inertia weight w ith number of iteration
由图2可知,较线性变化曲线,指数规律变化曲线能够确保在迭代前期(k较小)时,ω值较大;在迭代后期(k较大)时,ω值较小.
2.3 高斯扩张变异
PSO算法在运行过程中,若某粒子发现一个当前最优位置,则其他粒子将迅速向其靠拢,但此单一调整模式会不可避免地衍生如下问题:如果该最优位置为一局部最优点,粒子群将无法在解空间内重新搜索,此时算法陷入局部最优,出现早熟收敛现象.通常采用群体适应度方差σ2来判断算法是否陷入局部最优,其定义为:设粒子群的粒子数目为N,fi为第i个粒子的适应度,favg为粒子群目前的平均适应度,则群体适应度方差表示为
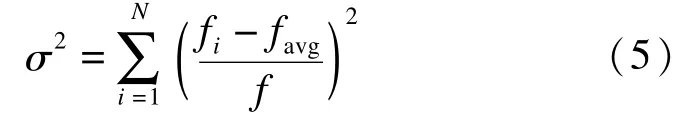
式中,f为归一化定标因子,用以限制 σ2的大小.f取值如式(6)所示.
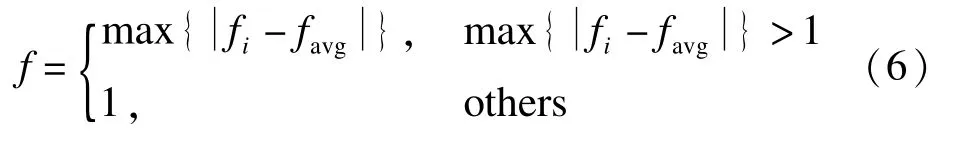
σ2反映粒子群中所有粒子的聚集程度,σ2越小,粒子聚集程度越大.如果 σ2<C(C为给定的某一阈值),且此时得到的最优解不是理论最优解或期望最优解,则可以判断算法陷入局部最优,出现早熟收敛.
针对早熟收敛现象,考察解的特性可知:此时的全局最优解一定是局部最优解.由式(1)可知,如果此时改变全局极值pgd,即可改变粒子的速度,让粒子进入其他区域进行搜索,在之后的搜索过程中,算法就可能发现新的个体极值pid和全局极值pgd,通过不断迭代,即可找到全局最优解.
对全局极值pgd采用扩张变异是解决早熟收敛的有效方法,表现为变异粒子在保持运动方向不变的情况下向前推移,在空间发生扩张性变化[10].若粒子在三维空间中从点 A(1,1,1)到点B(2,2,2)发生扩张变异,则各维的值均从1同步扩大到2,其变异算子为

基于上述改变,扩张变异表现为一种整体性的变化,加快了粒子跳出局部极值时间.本文对全局极值pgd的改变采用高斯扩张变异扰动机制,其变异算式为

式中,τ为服从Gauss(0,1)分布的随机变量.选取高斯扩张模式是由于其函数本身径向对称,解析性和光滑性好,且输入输出之间的映射作用在输入空间有限范围内为非零值,非常适用于在存在大量局部极值点优化问题中寻找到全局极值的情形.
3 PSO优化BP网络策略
实际系统中普遍存在着非线性因素.非线性建模的目的是实现一级变量与另外一级变量间的数学映射关系,关联信息可以是采样数据,也可以是一般性的描述,还可以是近似的数学关系等. BP网络是一种隐性的知识表达方法,采用并行计算的推理机制,非线性逼近精度与效率绝不亚于其他形式的非线性万能逼近器.BP(反向传播)的实现是确保可训练参数(权值向量及阈值向量)在有导师监督下,寻找到性能指标函数在参数空间变化率最大的方向,即数学上的梯度下降.
梯度下降本身致使算法易陷入局部极值,而全局逼近特性会拖慢学习收敛速度.借助上述改进的 PSO算法,提出由其优化 BP神经网络的初始权值和阈值.同时,为避免二进制编码的Ham-ming悬崖问题,将上述权值向量和阈值向量进行实数编码,作为PSO算法中的粒子,一方面可以不必进行数制转换,直接在解的变现型上进行优化操作;另一方面又确保引入了与问题邻域相关的启发式信息来增加算法的搜索能力.在适应度函数(fitness functions)的确定上,选择BP网络的均方误差函数以确保其永远非负.该辅助模式的实现流程如下:
1)由输入/输出样本集确定 BP网络的拓扑结构,将权值向量和阈值向量编码成实数向量,并表示为PSO算法中的粒子.
2)初始化PSO算法中的参数,确定种群最大迭代次数K,种群规模 N,惯性权重初值ωs和终值 ωe,学习因子c1和 c2,以及变异阈值 C,并根据网络结构确定粒子维数D.
3)利用混沌序列初始化粒子位置及速度,将粒子的初始位置设置为个体极值pid,将个体极值中最优值设置为全局极值pgd.
4)根据式(4)更新惯性权重 ω;根据式(1)、(2)更新粒子的速度和位置,并计算每个粒子的适应度值,以更新粒子个体极值和全局极值.
5)根据式(5)、(6)计算群体适应度方差σ2,如果σ2<C且此时算法的最优解未达到理论最优解,对全局极值pgd按式(8)进行变异操作;否则,转向步骤6).
6)如果迭代次数达到最大迭代次数或满足最小误差要求,迭代停止,将 PSO算法全局最优值pgd赋予 BP网络,即将全局极值映射为BP网络的初始权值和阈值;否则,返回步骤4)继续执行.
该改进PSO优化BP网络算法流程图如图3所示.
4 电力变压器故障诊断应用实例
将上述经 PSO优化且具有学习功能的BP网络用于变压器故障诊断模型中,并建立油中溶解气体的组分和含量与变压器故障类型间的对应关系.
4.1 网络模型描述
鉴于电力变压器油中溶解气体分析数据在一定程度上反应故障类型,采用油中气体 H2、CH4、C2H6、C2H4、C2H2体积分数百分比判定电力变压器故障类型,即BP网络的输入为五种气体占气体总和的百分比,网络的输出划分为五种故障类型,即五种模式,分别为:无故障、中低温过热(t<700℃)、高温过热(t>700℃)、低能放电(局部放电和比较微弱的火花放电)和高能放电(电弧放电和比较强烈的火花放电).

图3 改进PSO优化BP神经网络的流程图Fig.3 Flow chart of improved PSO optimized BPNN
4.2 算法参数设置
由某次收集的270组变压器故障数据构成样本空间,200组作为训练样本,余下 70组作为测试样本,同时为确保输入、输出样本值较均匀地落在[0,1]区间,先进行归一化处理.经试凑 BP网络的结构取5-15-5.相关参数设置如下:最大迭代次数K=1 000,种群规模 N=50,学习因子 c1=c2=2,惯性权重初值ωs=0.9,终值ωes
4.3 仿真结果分析
分别采用标准BP、PSO-BP及MPSO-BP对上述样本集进行仿真试验.图4给出了性能指标函数的收敛过程曲线.
显而易见,未经改进的BP方法学习收敛速度最慢,MPSO-BP较PSO-BP在500代前的收敛效率有明显提升,第500代时,MPSO-BP方法找到了全局最佳个体,即BP网络的最佳权值和阈值,该向量相当于1×170维的数组,在之后的500代,新参数加快了 BP网络的收敛速度,使训练误差在0.021 7处不再发生变化.

图4 三种算法的训练误差曲线对比Fig.4 Comparison in training error of three algorithms
表1给出了以70组训练测试后三种算法的诊断准确率及运行时间数据.MPSO-BP模型仍以BP网络为主体,在初始阶段对其权值向量和阈值向量进行编码,并在算法中通过粒子寻优提升 BP网络的收敛速度,进程确实拖慢了运行时间,但使诊断准确率有所提高(达到91%),使用者可在计算复杂度、效率及准确率等方面对相应方法做出选择.程序运行时间由Intel T4300、主频 2.2 Hz的计算机在Matlab7.0仿真环境下得出的.

表1 三种算法的故障诊断准确率Tab.1 Fault diagnosis accuracy rates of three algorithms
表2选取有代表性的10组诊断结果,表征对五种故障模式的判断过程,原 70组测试样本中的真实故障平均分配,即每种故障对应14个样本.

表2 部分故障案例诊断结果Tab.2 Diagnosis results for partial fault examples
由表2可知,BP算法对无故障模式、低能放电模式分别出现一次诊断错误,PSO-BP算法对中低温过热模式出现一次诊断错误,而MPSO-BP算法对低能放电模式出现一次诊断错误.经数值仿真及结果统计,三种算法下五种故障模式的诊断准确率如表3所示,其中,MPSO-BP算法诊断的高能放电的14组样本测试结果与实际情况完全相符,准确率达到100%.

表3 三种算法对各故障的诊断准确率比较Tab.3 Comparison in diagnosis accuracy rates of various faults w ith three algorithms
5 结 论
面向电力变压器故障诊断应用实际,借助BP网络的非线性万能逼近特性,结合DGA技术,实现BPNN离线训练与在线故障分析,对故障模式做出判断.提出改进的PSO优化BP初值和阈值向量策略,将混沌初始化、惯性权重指数形式调整及局部极值粒子高斯扩张变异等三种改进模式融合起来,以提升BPNN收敛速度,并解决标准PSO易陷入局部最优的应用局限.以实测的270组故障数据建立样本空间,仿真结果表明,MPSO-BP法更合理地更新了粒子的位置和速度,最优地设置了全局极值,有效克服了粒子的早熟收敛,并加快了收敛速度,使故障诊断准确率大幅提升.后续工作可进一步细化各种改进PSO模型的参数设置和适用范围,对其工程通用性做出评价.
(
):
[1]唐勇波,桂卫华,欧阳伟.基于相对重构贡献的变压器故障诊断方法 [J].高压电技术,2012,38(11):2964-2971.(TANG Yong-bo,GUI Wei-hua,OUYANG Wei. Transformer fault diagnosis method based on relative reconfiguration-based contribution[J].High Voltage Technology,2012,38(11):2964-2971.)
[2]Biswas D K,Panja SC,Guha S.Multi objective optimization method by PSO[J].Procedia Materials Science,2014,97(6):1815-1822.
[3]Nasir A,Algeelani M,Afendi M,et al.Hybrid regrouping PSO based wavelet neural networks for characterization of acoustic signals due to surface discharges on H.V.glass insulators[J].Applied Soft Computing,2013,13(12):4622-4632.
[4]孙延维,彭智明,李健波.基于粒子群优化与模糊聚类的社区发现算法[J].重庆邮电大学学报(自然科学版),2015,27(5):660-666.(SUN Yan-wei,PENG Zhi-ming,LIJian-bo.Community detection algorithm based on partide swarm optimization and fuzzy clustering[J].Journal of Chongqing University of Posts and Telecommunications(Naturnal Science Edition),2015,27(5):660-666.)
[5]郭雨梅,卢弘博.光栅莫尔条纹信号非正弦性误差修正[J].沈阳工业大学学报,2015,37(6):679-683.(GUO Yu-mei,LU Hong-bo.Non-sinusoidal error correction for grating Moire fringe signal[J].Journal of Shenyang University of Technology,2015,37(6):679-683.)
[6]马颖,田维坚,樊养余.基于云模型的自适应量子粒子群算法[J].模式识别与人工智能,2013,26(8):787-793.(MA Ying,TIAN Wei-jian,FAN Yang-yu.Adaptive quantum-behaved particle swarm optimization algorithm based on cloud model[J].Pattern Recognition and Artificial Intelligence,2013,26(8):787-793.)
[7]Shi Y H,Eberhart RC.A modified particle swarm optim izer[C]//Proceedings of the IEEE Congress on Evolutionary Computation.Anchorage,USA,1998:69-73.
[8]杜振鑫,王兆青.一种改进的动态改变惯性权重的粒子群算法[J].微电子学与计算机,2011,28(3):85-88.(DU Zhen-xin,WANG Zhao-qing.Improved PSO algorithm with dynamic change of inertia weights[J]. Microelectronic&Computer,2011,28(3):85-88.)
[9]张超,马金宝,冯杰.水文模型参数优选的改进粒子群优化算法[J].武汉大学学报,2011,44(2):182-186.(ZHANG Chao,MA Jin-bao,FENG Jie.Improved particle swarm optimization algorithm for parameter optimization of hydrologic models[J].Journal of Wuhan University,2011,44(2):182-186.)
[10]罗德相,周永权,黄华娟,等.多种群粒子群优化算法[J].计算机工程与应用,2010,46(19):51-54.(LUO De-xiang,ZHOU Yong-quan,HUANG Huajuan,et al.Multi-colony particle swarm optimization algorithm[J].Computer Engineering and Applications,2010,46(19):51-54.)
(责任编辑:景 勇 英文审校:尹淑英)
Fault diagnosis and pattern recognition of power transformer based on im proved PSO-BPNN
XIA Lin-lin1,WEN Lei1,LIU Hui-m in2,CHU Yan3,TAI Jin-juan1
(1.School of Automation Engineering,Northeast Electric Power University,Jilin 132012,China;2.College of Mechanical and Electrical Engineering,Qingdao Agricultural University,Qingdao 266109,China;3.College of Computer Science and Technology,Harbin Engineering University,Harbin 150001,China)
In order to optimize the relative learning parameters for back propagation neural network(BPNN),a novel particle swarm optimization(PSO)aided BPNN method was proposed.The fault features were established with the gas volume fraction in the oil of power transformer.In addition,the initial weight and threshold values of BPNN were coded in real number form,and were related to the particles in the PSO.The off-line training and on-line analysis of BPNN were realized,and the fault patterns of transformer were judged.The results show that the algorithm updates the position and velocity of particles more reasonably,and the global extremum is optimally set.The premature convergence of particles is effectively overcome,and the accuracy rate of fault diagnosis approaches as high as 91%.Besides,the convergence rate of BPNN gets dramatically enhanced,and the mentioned algorithm provides an effective model reference for this sort of designs.
particle swarm optimization(PSO)algorithm;chaos initialization;inertia weight;Gauss extension mutation;BPNN method;power transformer;fault diagnosis
TM 407
A
1000-1646(2016)06-0606-06
10.7688/j.issn.1000-1646.2016.06.02
2016-03-14.
国家自然科学基金青年基金资助项目(61503073);吉林市杰出青年基金资助项目(20166005).
夏琳琳(1980-),女,吉林松原人,副教授,博士,主要从事人工智能、数据融合等方面的研究.
11-07 12∶30在中国知网优先数字出版.
http:∥www.cnki.net/kcms/detail/21.1189.T. 20161107.1230.006.htm l

