基于秩约束逼近的系统模型降阶
李久芹,杨洪礼
(山东科技大学 数学与系统科学学院,山东 青岛 266590)
基于秩约束逼近的系统模型降阶
李久芹,杨洪礼
(山东科技大学 数学与系统科学学院,山东 青岛 266590)
针对Daniel Ankelhed在2007年根据控制器设计原理提出的降阶模型,利用秩函数、核范数、谱范数与线性矩阵不等式的相互关系,将秩约束条件转化为线性矩阵不等式,使原降阶模型变为凸优化模型。数值试验表明降阶效果良好。
系统降阶;秩约束条件;线性矩阵不等式;凸优化模型
工程应用领域中常常涉及到大型或者复杂动力系统的设计、仿真、优化和控制,这个系统一般都是由微分或差分方程来描述,方程的维数通常比较高,物理或者工程实现比较困难。系统模型降阶十分必要,降阶方法是控制理论与应用研究领域中的热点问题。高阶系统的降阶方法有很多,其中较为有效的是K.Glover[1]于1984年提出的Hankel范数降阶模型和Moore[2]在1981年提出的平衡截断模型。这两种方法都能有效地降低高阶系统的阶次,且既能保持原系统的可观、可控性及稳定性,又能得到降阶系统与原始系统的误差关系。
Daniel Ankelhed[3]从控制器的设计出发,将系统降阶原理与控制器设计原理相结合,建立了系统降阶模型。然而模型中的秩约束条件是不连续且不可微的,使得模型难以求解。结合对控制系统的最新研究[4-6],本文基于秩函数、核范数、谱范数与线性矩阵不等式的相互关系,将模型中的秩约束条件改为线性矩阵不等式,使其成为凸优化模型,并通过实例验证其有效性。
Sn是n×n阶对称矩阵的集合,Rm×n是m×n阶实矩阵的集合,A>0(A≥0)指A是正定(半正定)矩阵,A<0(A≤0)指A是负定(半负定)矩阵,A†指矩阵A的广义逆,G(s)=C(sI-A)-1B+D是系统的转换函数。
1 预备知识
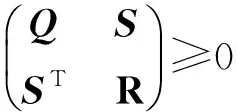
引理2(非严格消除引理)[8]给定矩阵G∈Rn×n,U∈Rn×m,V∈Rn×p使得U的值域和V的值域是线性独立的。则存在X∈Rm×p使得G+UXVT+VXTUT≤0成立,当且仅当U⊥GU⊥T≤0且V⊥GV⊥T≤0成立。其中U⊥、V⊥分别是U、V的正交矩阵。
引理3(非严格有界实引理)[9]令H(s)=C(sI-A)-1B+D、
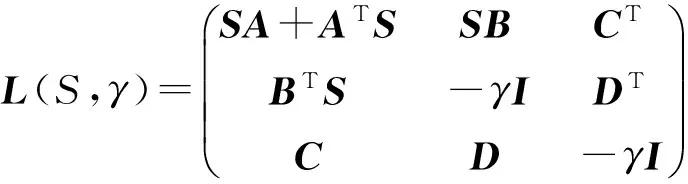

引理4[10]假设X=XT∈Rn×n,Y=YT∈Rn×n,r是一个正数,则下面的描述是等价的:
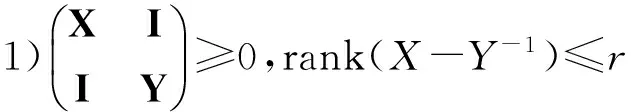
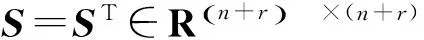

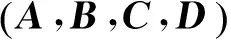
AP+PAT+BBT=0,
(1a)
ATQ+QA+CTC=0。
(1b)

AP+PAT+BBT≤0,
(2a)
ATQ+QA+CTC≤0。
(2b)

引理5[11]对于任意的秩最大为r的矩阵X,其谱范数、Frobenius范数、核范数三者之间满足:
(3)
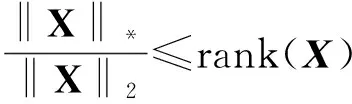
推论2[12]对于任意满足‖X‖2≤1的矩阵,则‖X‖*≤rank(X),即在谱范数定义的单位球上核范数是矩阵秩的一个凸下界。
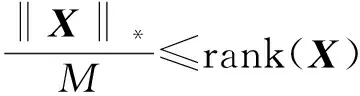
引理6[11]Z是m×n维矩阵,若其谱范数小于等于常数t,则可表示成一个线性矩阵不等式:
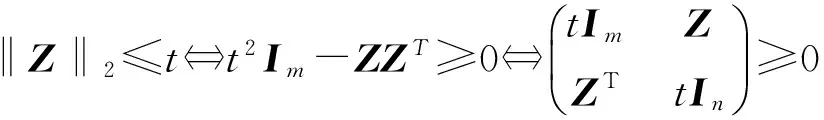
(4)


(5)

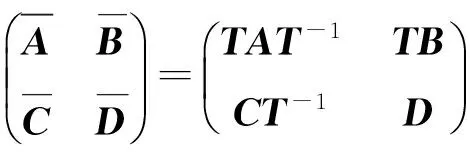
(6)
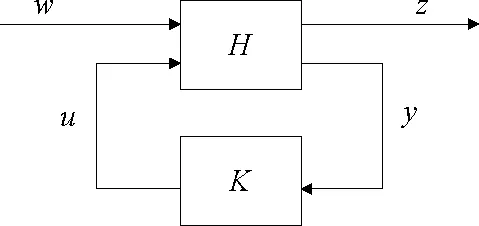
图1 带有装置H和控制器K的 标准H∞控制器设计框架Fig.1 The standard H∞ controller design framework with device H and controller K
2 H∞控制器设计
为使从输入ω到输出z的H∞范数变小,利用带有线性矩阵不等式的H∞控制器设计框架,找到一个控制器K。装置H和控制器K之间的关系如图1所示。
利用状态空间形式,装置H可以被分为下面的形式:

(7)
假定系统是可控和可观的,该装置可解决一系列的控制器设计问题。线性矩阵不等式方法可以用来解决控制器的设计问题。根据(7)式的划分,状态空间形式变为:

z=C1x+D11ω+D12u;
y=C2x+D21ω+D22u。

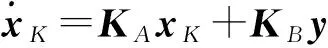
u=KCxK+KDy。
其中,KA∈Rk×k保证了性能界限γ,在指数K下,令D22=0,则闭环系统状态空间矩阵可表示为:
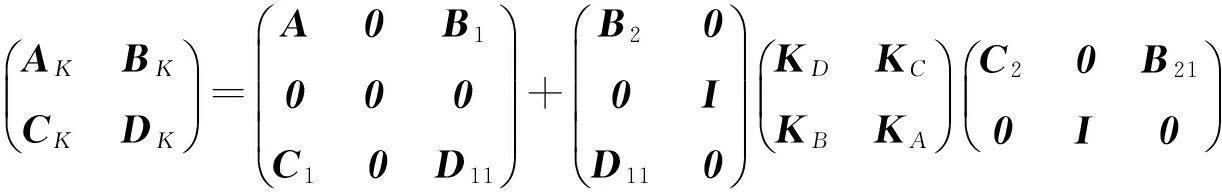
(8)
其中,AK∈R(n+k)×(n+k)。
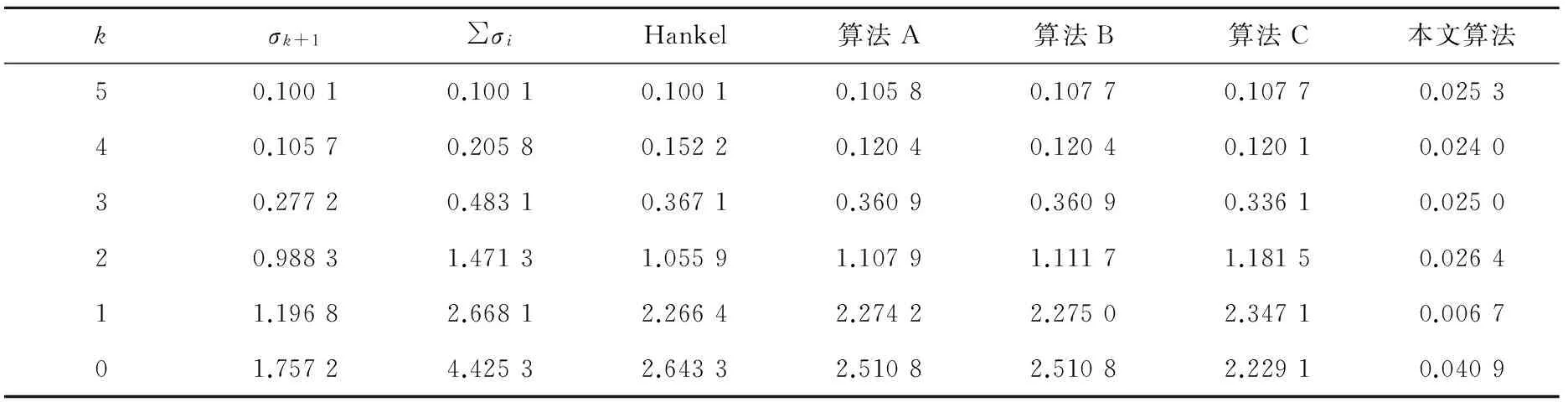
由引理3可知,如果该闭环系统是稳定的,则存在正数γ和0 (9) 将(8)式代入(9)式,再结合引理4中的第二个条件可得: (10a) (10b) (10c) (10d) 3.1 原始模型 图2 原始系统Gn与降阶系统k关系图Fig.2 The relationship between the originalsystemGn and the reduced order 假设原始系统阶数为n,降阶系统的阶数为k,则系统的降阶问题可描述为以下模型: minγ (11a) (11b) k (11c) 其中,γ是模型降阶误差的上界,根据图2,模型降阶问题可以被看成是H∞控制器设计问题,问题(11)中H(s)可以被定义为下列形式: (12) 令Q=γX,P=γY,由舒尔实现定理(引理1)可知,降阶问题可描述为下列形式: minγ (13a) s.t QA+ATQ+CTC≤0 (13b) AP+PAT+BBT≤0 (13c) (13d) rank(QP-γ2I)≤k (13e) γ>0,P,Q∈Sn (13f) (13)式中,秩约束条件是非凸的,难以用线性矩阵不等式求解。用凸约束来近似秩约束,一般有两种方法:一是容许一部分不可行解存在,扩大可行域;二是减少部分解,承认优化解可能不存在,缩小可行域。本文采取第二种方法,利用秩函数、核范数、谱范数与线性矩阵不等式的相互关系,将秩约束条件转化为线性矩阵不等式,缩小可行域。 3.2 凸优化降阶模型 定理3[13]设A,B为n阶正定矩阵,矩阵A的n个特征值为0<λ1≤λ2≤…≤λn,矩阵B的n个特征值为0<μ1≤μ2≤…≤μn,则矩阵AB的特征值λ∈[λ1μ1,λnμn]。 推论5[13]设A,B为n阶半正定矩阵,矩阵A的n个特征值为0≤λ1≤λ2≤…≤λn,矩阵B的n个特征值为0≤μ1≤μ2≤…≤μn,则矩阵AB的特征值λ∈[0,λnμn]。 (trace(P)+trace(Q))2 令P,Q为常数矩阵,则模型(13)转化为下列凸优化问题: minγ; (14a) s.tQA+ATQ+CTC≤0; (14b) AP+PAT+BBT≤0; (14c) (14d) (14e) γ>0,P,Q≥0。 (14f) 2) 确定降价后的系统阶数k; 3) 根据模型(14)求出误差γ; 考虑如下系统[3],系数矩阵为: 计算可得,系统的Hankel奇异值为σ1=2.175 4,σ2=0.105 2,σ3=0.099 3。利用YALMIP[14]软件编写程序,得到结果如表1所示。 表1 降阶误差对比Tab.1 Reduced order error contrast 根据上述算法,当系统降为1阶、2阶时,降阶系统分别为: 例2: 。 系统的Hankel奇异值为σ1=0.874 3,σ2=0.030 4,σ3=0.020 2,σ4=0.019 7,σ5=0.005 2。利用YALMIP[14]软件编写程序,得到结果如表2所示。 根据上述算法,当系统降为4阶时,降阶系统为: ,其中,。 表2 降阶误差对比Tab.2 Reduced order error contrast 系统的Hankel奇异值为σ1=1.757 2,σ2=1.196 8,σ3=0.988 3,σ4=0.277 2,σ5=0.105 7,σ6=0.100 1。利用YALMIP[14]软件编写程序,得到结果如表3所示。 表3 降阶误差对比Tab.3 Reduced order error contrast 根据上述算法,当系统降为3阶时,降阶系统分别为: 利用秩函数、核范数、谱范数与线性矩阵不等式的相互关系,将秩约束条件转化为线性矩阵不等式约束,得到凸优化模型。该优化模型求解简便,弥补了秩约束条件不连续不可微的缺点。通过数值实验,将改进后的模型与文献[3]中的降阶模型进行误差比较,得到的降阶误差小于文献[3]中的误差,说明改进后的模型降阶效果良好。 [1]GLOVER K. All optimal Hankel-norm approximations of linear multi-variable systems and theirL∞-error bounds [J]. International Journal of Control,1984,39(6):1115-1193. [2]MOORE B.Principal component analysis in linear systems:Controllability, observability and model reduction [J]. IEEE Transactions on Automatic Control,1981,26(1):17-32. [3]ANKELHED D, HELMERSSON A, HANSON A. Suboptimal model reduction using LMIs with convex constraints [J]. European Control Conference,2007,12(11):3-8. [4]BESSELINK B,TABAK U, et al. A comparison of model reduction techniques from structural dynamics, numerical mathematics and systems and control[J]. Journal of Sound and Vibration,2013,332(19):4403-4422. [5]ELIAS J,TOBIAS D,WIM M. Model reduction of time delay systems using position balancing and delay Lyapunovequations[J].Mathematics of Control,Signals and Systems, 2013,25(2):147-166. [6]SREERAM V,SAHLAM S. Improved results on frequency weighted balanced truncation and error bounds[J]. International Journal of Robust and Nonlinear Control, 2012,22(11):1195-1211. [7]BOYD S, EL GHAOUI L, FERON E, et al. Linear matrix inequalities in system and control theory[M]//Society for Industrial and Applied Mathematics,1997:27-29. [8]HELMERSSON A. Methods for robust gain scheduling[D]. Sweden:Dissertation Linkoping University, 1995:1-221. [9]SCHERER C. The Riccati Inequality and State-SpaceH∞-Optimal Control[D]. Germany:University of Wurzburg,1990:1-266. [10]PACKARDA.Gainschedulingvialinearfractionaltransformations[J].SystemsandControlLetters, 1994,22(2):79-92. [11]徐芳芳. 矩阵补全的模型、算法和应用研究[D]. 上海:上海交通大学,2014:1-117. [12]FAZELM.Matrixrankminimizationwithapplications[D].Stanford:StanfordUniversity, 2002:1-130. [13]唐建国. 两实对称矩阵乘积特征值的上下界[J]. 延边大学学报(自然科学版),2009,35(4):1-3.TANGJianguo.Upperandlowerboundsoftheeigenvaluesoftheproductoftworealsymmetricmatrices[J].JournalofYanbianUniversity(NaturalScience),2009,35(4):1-3. [14]EFBERGJ.YALMIP:AtoolboxformodelingandoptimizationinMATLAB[C] //IEEEInternationalSymposiumonComputerAidedControlSystemsDesign.Taipei,Sept.2-4, 2004:287-292. (责任编辑:傅 游) System Model Order Reduction Based on Rank Constraints Approximation LI Jiuqin, YANG Hongli (College of Mathematics and Systems Science, Shandong University of Science and Technology, Qingdao, Shandong 266590, China) To improve the reduced order model proposed by Daniel Ankelhed in 2007 according to the controller design principle, the rank constraint was transformed into a linear matrix inequality and the reduced order model was transformed into a convex optimization model by using rank function, the nuclear norm, spectral norm and linear matrix inequality in relation to each other. Results of numerical tests indicate that the effect of this model is favorable. system order reduction; rank constraint; linear matrix inequality; convex optimization model 2016-04-15 国家自然科学基金项目(11241005) 李久芹(1990—),女,山东济南人,硕士研究生,主要从事最优控制理论与应用方面的研究。 杨洪礼(1974—),男,山东临沂人,副教授,博士,主要从事优化理论与算法、最优控制理论与应用、非负矩阵与张量分解等方面的研究,本文通信作者. E-mail:yhlmath@126.com O231.1 A 1672-3767(2016)06-0114-09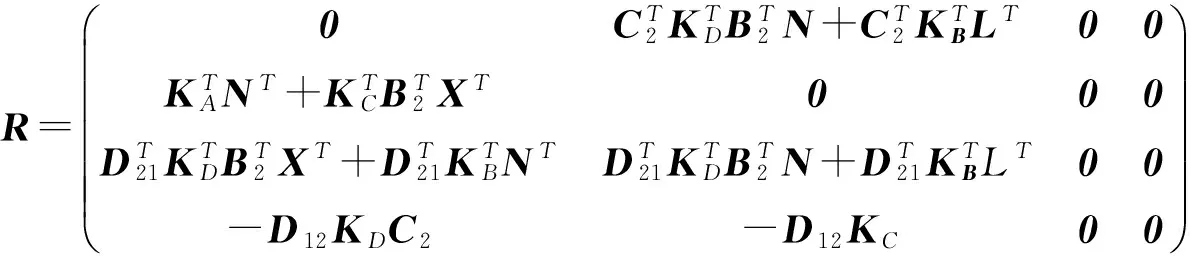

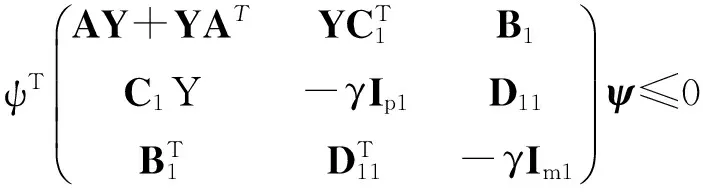
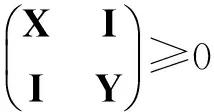

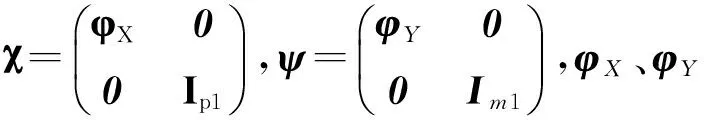
3 模型降阶

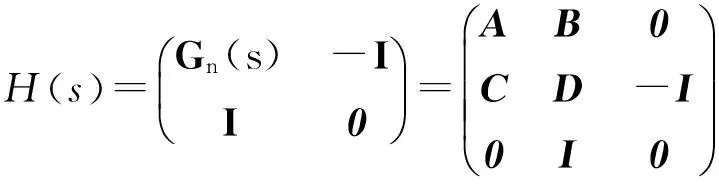
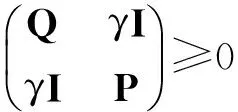
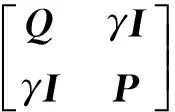
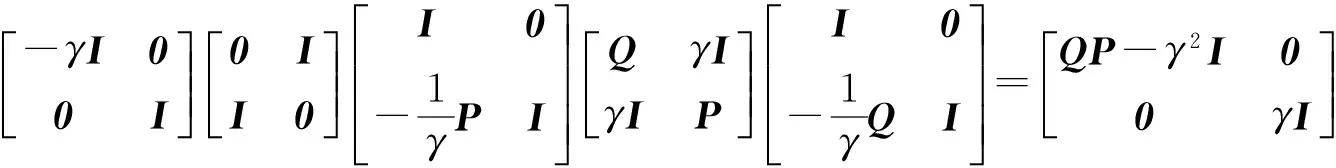
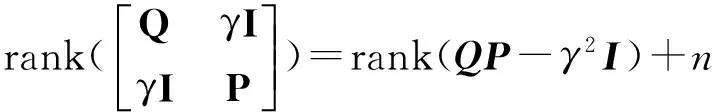
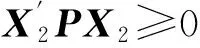
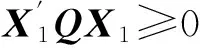
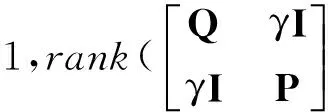
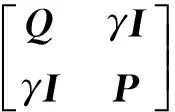
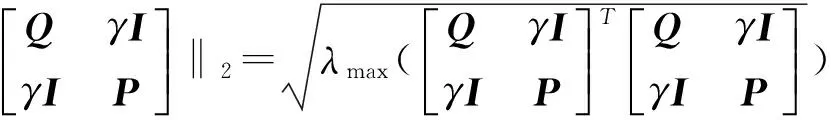
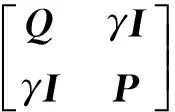
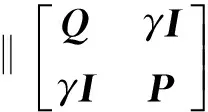
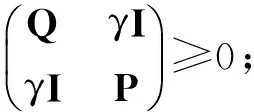
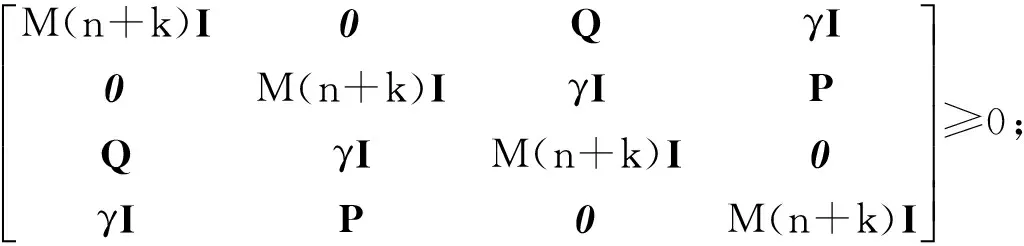
4 模型算法

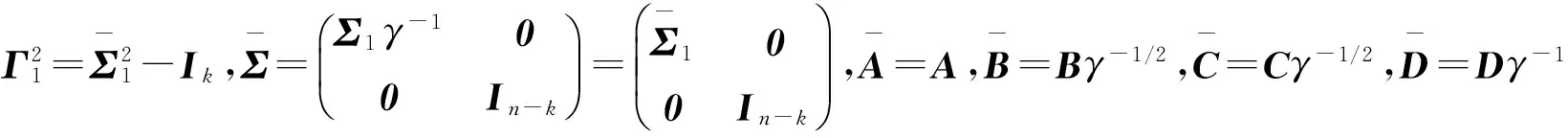
5 数值实验
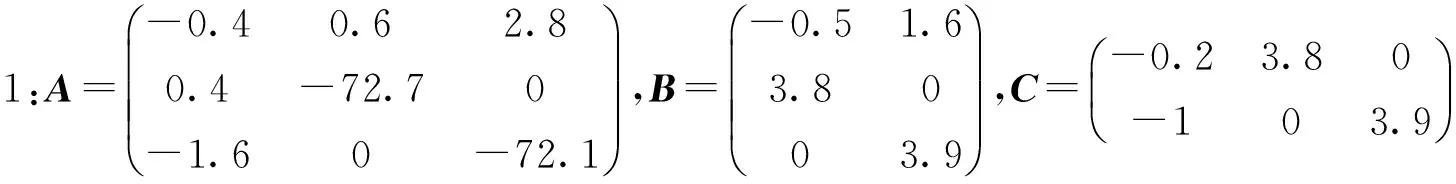

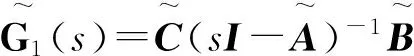


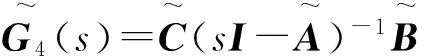


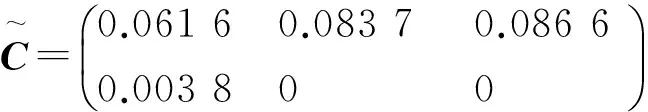
6 结论

