方差分析在跳水运动成绩管理中的应用

戴金辉，代金辉

（山东工商学院a.统计学院；b.数学与信息科学学院，山东 烟台264005）

方差分析在跳水运动成绩管理中的应用

戴金辉a，代金辉b

（山东工商学院a.统计学院；b.数学与信息科学学院，山东 烟台264005）

跳水运动员的成绩普遍采用裁判员打分的形式，所以跳水运动员的成绩除了受运动员动作完成情况影响外，还受到裁判员主观因素的影响。文章采用有交互作用的双因素方差分析方法，对跳水运动员成绩进行评价，分析运动员、裁判员和裁判员对运动员的主观因素对跳水运动员成绩的影响，为客观、公正评价运动员的成绩和裁判员评分水平，提供了理论支持。

跳水比赛；有交互作用的双因素方差分析；成绩评定

0　引言

跳水是一项优美的水上运动，它是指运动员从高处用各种姿势跃入水中或是从跳水器械上起跳，在空中完成一定动作姿势，并以特定动作入水的运动。在比赛中，裁判员需要根据运动员完成动作的情况来评分。运动员比赛成绩受到运动员动作完成情况影响，同时也受到裁判员主观因素的影响。裁判员作为比赛的一个重要组成部分，裁判员应该严格执行竞赛规则制度，保证比赛公平、公正、顺利的进行，但是裁判员个人对比赛规则理解的深度和执行的力度在一定程度上影响着运动员的成绩，所以裁判员的作用就变得更为重要，所以如何科学的对裁判员进行监督和评价，也成为一个亟待解决的课题。

1　跳水比赛的成绩评定

跳水比赛要完成五个规定动作，分别是一次向前跳水、一次向后跳水、一次反身跳水、一次向内跳水和一次向前跳水转身半周。在比赛中，常用的方法是多名裁判员打分，去除一个最高分和一个最低分（如果裁判员人数较多，去除两个最高分和两个最低分），计算剩下的有效分的平均数，这种比赛计分方法更为普遍，这是一种简单、可行、有效的方法，但是这种方法有多少科学性值得探究，可能会出现动作完成情况不同的两名运动员比赛成绩却是相同的情况。

同时，某些裁判员（给出最高分和最低分的裁判员）的意见也被忽视，在计算比赛成绩时去掉他们的评分就是否定他们的意见，站在统计学的角度看，这也是信息没有得到充分利用。如果评价裁判员执法水平的依据是裁判员评分偏离运动员最终得分的程度，容易影响到裁判员的主观意愿，担心自己给出的评分太高或者太低，这就产生了折中评分倾向，违背了裁判员的真实想法，同时也使评分的区分度降低，运动员成绩的差距缩小，形成执法的偏差。

如果把跳水运动员在比赛中完成动作情况看成是实验，那么裁判员评分就可以看作是实验结果，影响这一结果的因素有运动员和裁判员两方面因素，裁判员个人主观偏好也会影响运动动员成绩，并且，在一次比赛中，裁判员的数量是确定的，这样我们可以用有重复双因素方差分析法来研究跳水运动员成绩。

2　可重复双因素方差分析

2.1数据结构

在双因素方差分析中，由于有两个因素同时起作用，在获取数据时，要将运动员安排在“行”的位置，称为行因素；比赛进行的轮数安排在“列”的位置，称为列因素。本文假定有k个运动员，即是有k个水平：行1，行2，…，行k；规定动作有r个，即是有r个水平：列1，列2，…，列r。第i个运动员在第 j个动作的成绩即是一个组合(Ai，Bj)，每一组合都有t(t＞1)名裁判员，观察数据结构（见表1），这样共抽取了krt个观测数据。

表1　有交互作用的双因素方差分析数据结构

在进行有交互作用的双因素方差分析时，常用的表示符号有：xijl为对应于第i个水平行因素、第 j个水平列因素、第l行的观测值；是第i个水平行因素的样本均值，是第 j个水平列因素的样本均值，为对应于第i个水平行因素和第 j个水平列因素组合的样本均值，为所有n个观测值的均值，

2.2分析步骤

有交互作用的双因素方差分析步骤：

第一步：提出原假设与备择假设

由于有两个影响因素同时对实验结果产生影响，并且两者之间不是相互独立的，还有交互作用，所以要同时对行因素、列因素、行因素和列因素交互作用，共提出三种假设，分别是：

（1）对行因素对实验结果是否有显著性影响提出假设

H0A:μ1=μ2=…=μi=…=μk（运动员对最终成绩不产生显著性的影响）

H1A:μ1，μ2，…，μi，…，μk不全相等（运动员对最终成绩产生显著性的影响）

（2）对列因素对实验结果是否有显著性影响提出假设

H0B:μ1=μ2=…=μj=…=μr（规定动作对最终成绩不产生显著性的影响）

H1B:μ1，μ2，…，μj，…，μr不全相等（规定动作对最终成绩产生显著性的影响）

（3）对行因素与列因素交互作用对实验结果是否有显著性影响提出假设

H0AB:μ1=μ2=…=μj=…=μr（裁判员认可运动员规定动作的完成程度对最终成绩不产生显著性的影响）

H1AB:μ1，μ2，…，μj，…，μr不全相等（裁判员认可运动员规定动作的完成程度对最终成绩产生显著性的影响）

第二步：构造检验统计量

总平方和SST：

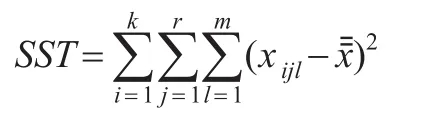
对总平方和进行分解：

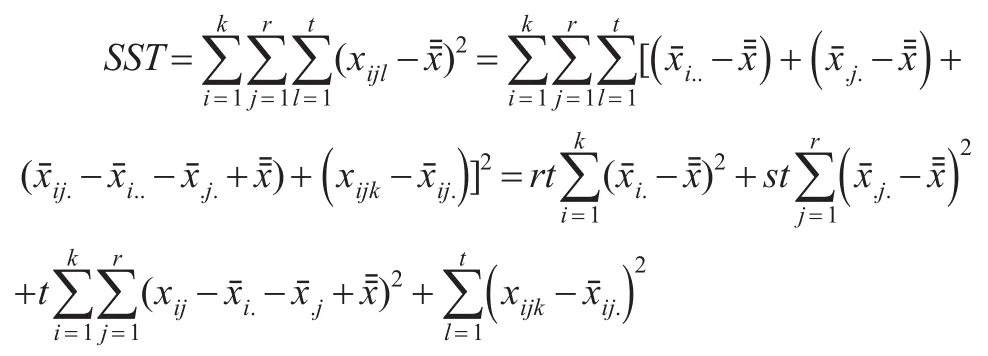
行变量平方和SSR是行均值xˉi..与总均值xˉ之间的离差平方和：

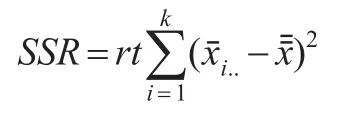
列变量平方和SSC是列均值xˉ.j.与总均值xˉ之间的离差平方和：

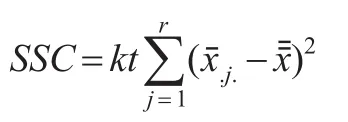
交互作用平方和SSRC：

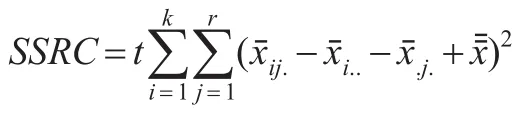
离差项平方和SSE指除行因素和列因素之外，由剩余因素影响产生的离差平方和：

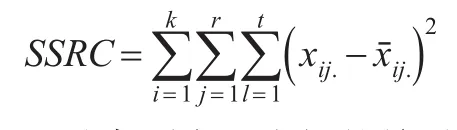
上述各平方和之间的关系式为；

四个平方和对应的自由度分别为：SST的自由度为kr-1；SSR的自由度为k-1；SSC的自由度为r-1；SSRC的自由度为（k-1）（r-1）；SSE的自由度为kr(t-1)-1。

为构造检验统计量，需要计算各个平方和的均方：

行因素的均方，简记为MSR，计算公式为：

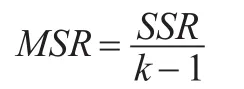
列因素的均方，简记为MSC，计算公式为：

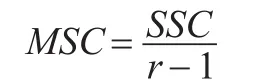
行因素与列因素交互作用的均方，简记为MSRC，计算公式为：

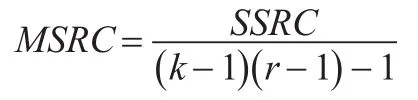
随机离差项的均方，简记为MSE，计算公式为：

所以，行因素对因变量影响显著性检验的统计量为：

列因素对因变量影响显著性检验的统计量为：

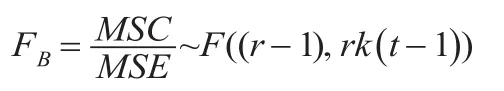
行元素与列因素交互作用对因变量影响显著性检验的统计量为：

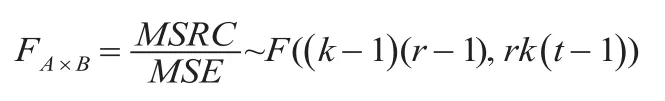
第三步：做出统计决策

若FA＞Fα，则拒绝原假设H0，表明运动员对最终成绩产生显著性的影响；反之，若FA＜Fα，则不拒绝原假设H0，表明运动员对最终成绩不产生显著性的影响。

若FB＞Fα，则拒绝原假设H0，表明规定动作对最终成绩产生显著性的影响；反之，若FB＜Fα，则不拒绝原假设H0，表明规定动作对最终成绩不产生显著性的影响。

若FA×B＞Fα，则拒绝原假设H0，表明裁判员认可运动员规定动作的完成程度对最终成绩产生显著性的影响；反之，若FA×B＜Fα，则不拒绝原假设H0，表明裁判员认可运动员规定动作的完成程度对最终成绩不产生显著性的影响。

此结果也可以用P值来表示。

以上内容列成方差分析表，见表2所示。

表2　方差分析

3　方差分析结果比较

在表3中，第4个类型是最好的，因素A差异显著，因素B差异不显著，因素A与因素B交互作用A×B不显著，是评分最佳结果，因为它在把跳水运动员动作水平区别开的同时，避免了比赛规定动作之间的差异和裁判员对比赛结果的影响。

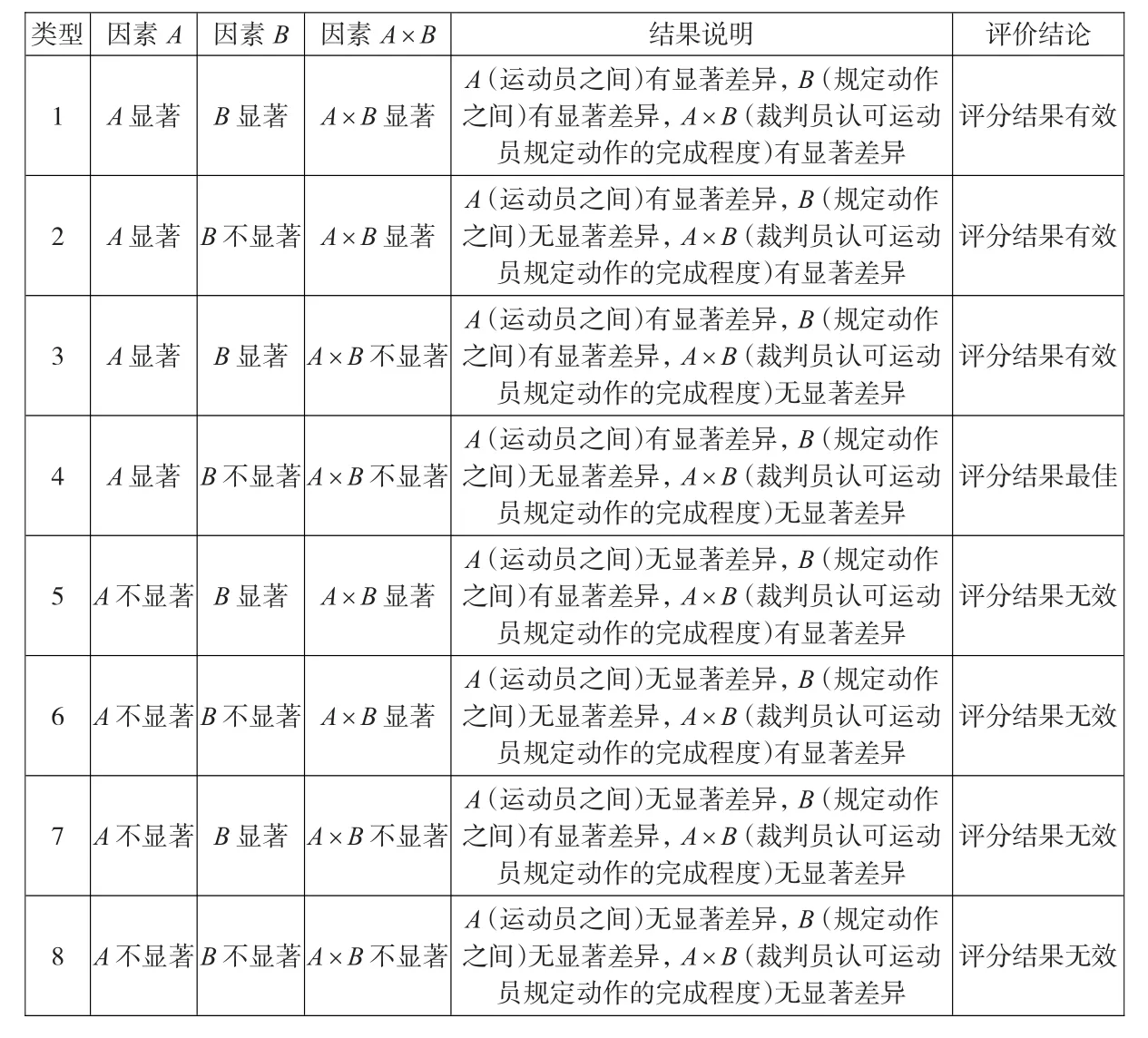
表3　方差分析的八种典型结果分析

4　实例分析

某次单人三米板比赛采取7人制打分，现在有6名运动员，共进行了5次规定动作跳水，分别是一次向前跳水、一次向后跳水、一次反身跳水、一次向内跳水和一次向前跳水转身半周。试根据比赛成绩分析运动员、规定动作、裁判员认可运动员规定动作的完成程度对比赛成绩的影响，比赛成绩见表4所示。（α=0.05）

根据上文介绍的公式，按计算过程逐步进行计算，对

表4　比赛成绩数据

计算结果进行整理，得到方差分析表，见表5。

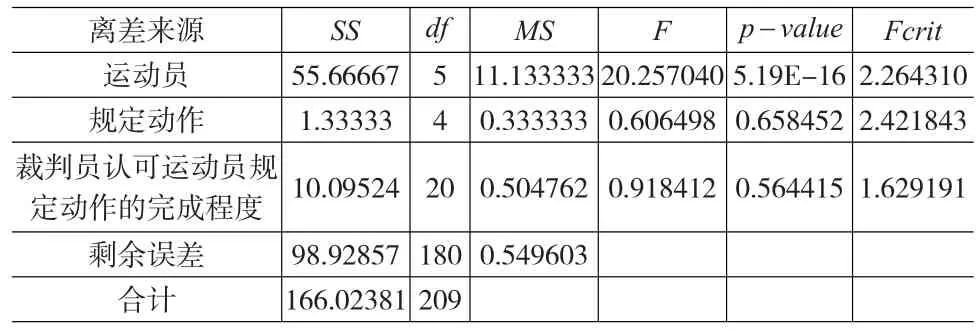
表5　有交互作用的双因素方差分析结果

由表5的结果可知：用于检验运动员的 p值= 5.19×10-16＜α=0.05，所以拒绝原假设，表明不同跳水运动员的完成动作水平之间有显著差异；用于检验规定动作的p值=0.658452＞α=0.05，不拒绝原假设，表明不同规定动作之间对比赛成绩没有显著差异，因为一个好的运动员应该能够出色的完成所有的规定动作；用于检验交互作用（裁判员认可运动员规定动作的完成程度）的p值=0.564415＞α=0.05，因此不拒绝原假设，表明裁判员认可运动员规定动作的完成程度对比赛结果没有显著影响，属于上文介绍的第4种类型方差分析，该评分结果表现出了跳水运动员动作的差异，但是没有表现出规定动作之间的差异，也没有表现出裁判员对运动员的主观偏好，所以此评分结果为最佳，裁判员的评分结果可靠。

5　结语

通过对有交互作用的双因素方差分析，可以评估运动员水平、规定动作设置是否合理和裁判员的裁判水平，从而确保跳水比赛公平、公正的进行，最终使运动员的动作规范在一个较高的水平。此种评价方法对于艺术体操、花样滑冰、蹦床、健美操等比赛项目也同样适用。

[1]贾俊平.统计学——基于SPSS[M].中国人民大学出版社，2014.

[2]韩之俊，蔡小军.方差分析在人力资源考评中的应用[J].南京理工大学学报，2003，（5）.

（责任编辑/浩天）

O212.1

A

1002-6487（2016）22-0080-03

山东省社会科学规划研究项目（15DJJJ14）；山东工商学院教改项目（11688JXYJ2015016）

戴金辉（1978—），女，辽宁凌源人，硕士，讲师，研究方向：统计分析。代金辉（1981—），女，黑龙江齐齐哈尔人，博士研究生，讲师，研究方向：统计分析。