混凝土循环加卸载动态损伤演化推移分析及损伤值估计模型

吴 彬，胡伟华，唐克静，文沛军

(1.湖北工业职业技术学院 建筑工程系， 湖北 十堰 443000；2.十堰市建筑设计研究院 ，湖北 十堰 443000;3. 三峡地区地质灾害与生态环境湖北省协同创新中心 ，湖北 宜昌 443002；4. 五矿二十三冶建设集团第一工程有限公司，湖南 湘潭 411100)



混凝土循环加卸载动态损伤演化推移分析及损伤值估计模型

吴 彬1,3，胡伟华2,3，唐克静1，文沛军4

(1.湖北工业职业技术学院 建筑工程系， 湖北 十堰 443000；2.十堰市建筑设计研究院 ，湖北 十堰 443000;3. 三峡地区地质灾害与生态环境湖北省协同创新中心 ，湖北 宜昌 443002；4. 五矿二十三冶建设集团第一工程有限公司，湖南 湘潭 411100)

利用多功能三轴仪进行了不同应变速率下的混凝土循环加卸载试验，对声发射信号与应力水平的关系进行了分析，并从声发射撞击数的角度对混凝土损伤演化规律特性进行研究，进一步构建了只含循环次数的单参数损伤值估计模型。研究结果表明：在不同的应变速率下，混凝土损伤演化的路径各不相同，当应变较小时，混凝土前期损伤累积程度较大，后期平缓，出现水平段；随着应变速率的提高，混凝土损伤演化路径前移，后一种应变速率相对于前一应变速率所对应的损伤推移值随着累计残余应变的增大呈现出先增大后减小的规律，当累计残余应变一定的情况下，随着应变速率的提高,相邻2种应变速率对应的损伤推移程度在不断减弱；混凝土循环加卸载损伤演化规律具有三阶段损伤模式，统计密度函数能较好地反映循环加卸载损伤演化规律。

混凝土；循环加卸载；动态损伤；声发射；损伤推移

1 研究背景

处于地震条件下的混凝土结构或构件往往承受来自正反2个方向的反复加载和卸载的过程。反复荷载作用下混凝土材料受力特点、变形特点以及破坏特征都与其他荷载类型作用时不同。由于循环加卸载试验对试验设备及相关的技术条件要求较高，目前国内外对循环荷载作用下的混凝材料试验研究相对较少，已有的相关成果[1-5]主要集中在力学特性的分析上，对其损伤的方面研究就显然不足了。总体而言，对于循环荷载作用下混凝土的研究大致遵循从静态到动态，从性能到本构的原则。关萍等[6]通过在不同应变率下进行单轴反复荷载的动态抗压试验，研究了混凝土抗压强度、弹性模量、峰值应变、应力应变曲线的性能随应变速率的变化规律。通过等应变增量的循环加卸载试验，周洪涛[7]对动态循环加卸载条件下混凝土的基本物理力学参数、强度硬化、刚度退化等进行了率效应分析，利用声发射技术对材料损伤演化与破坏过程进行了一定的分析。李淑春等[8]在混凝土反复荷载作用下的滞回规则的基础上，建立了考虑反复荷载作用下混凝土应力跌落、强度下降、刚度退化等力学性能的损伤模型。

国内外现有的关于循环加卸载损伤模损伤演化模型涉及的参数较多，给实际工程的应用带来较大困难。为此，本文进行了4种不同应变速率下(10-5，10-4，10-3，10-2s-1)的循环加卸载试验，从声发射的角度提出了新的单参数损伤值估计模型。

2 试验概况

试验采用强度等级为C30的标准立方体的试件。试验所用加载设备为10 MN微机控制电液伺服大型多功能动静力三轴仪(型号TAZW-10 000)，它主要由控制系统、伺服控制系统、加载框架、液压油泵系统等几部分组成。加载系统轴向最大动、静力加载值分别为5 000，10 000 kN，该系统主要有位移、变形和负荷3种控制方式。变速率响应范围为10-5～10-2s-1，能很好地满足试验的要求，试验加载装置图如图1所示。

图1 加载装置Fig.1 Loading device

试验主要步骤如下：

(1)试样的装配。用磨砂纸对试件前后中心位置(声发射探头黏贴处)进行打磨，去除表面的污渍或灰层；试件对中整平后安装好竖向变形计。

(2)声发射探头安装及检查。黏贴声发射探头(耦合剂采用黄油)；对安装好的探头进行脉冲标定测试，检查其连接是否完好。

(3)建立声发射记录文件、设置参数文件。根据材料性质、试验条件设置声发射参数。设置参数：采样频率：833 kHz，采样长度点数：2 048，撞击锁闭时间:300 μs，峰值鉴别时间：50 μs，撞击鉴别时间100 μs，信号门槛45 db，前置放大：40 db，主放大器：20 db，滤波器：20～100 kHz。

(4)加载。①预加载，先用EDC1控制指令使油缸上顶，在快要和传力柱接触时，声发射数据开始采集。继续加载到达10 kN,待力稳定时，再预加到30 kN，使试件与竖向传感器充分接触;②竖向正式加载，竖向按事先设置好的加载程序开始加载，同时采集声发射数据。加载完成后，声发射采集停止，建立第3个声发射数据文件。

3 声发射信号与应力水平的关系

试验得到的声发射撞击数与应力水平的对应关系见图2。其中σ0为峰值应力；Zmax为撞击数最大值；Z为撞击数瞬时值。

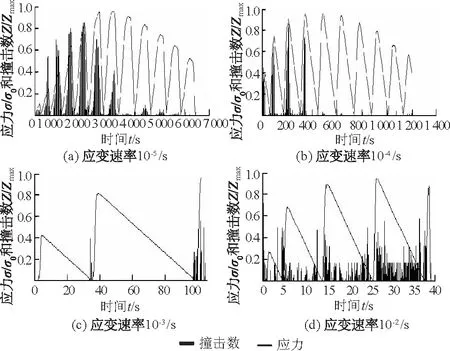
图2 声发射撞击数与应力的关系Fig.2 Relationship between acoustic emission hit number and stress

从图2可以看出，在单个循环加卸载过程中，声发射信号主要出现在加载阶段，卸载阶段出现的很少。在整个循环加卸载试验过程中，声发射信号主要集中在峰值应力以前，峰值应力以后出现的很少。在不同应变速率下，加载前期混凝土试件只在经历了曾经受到的最大应力水平时才产生较为明显的声发射，但是加载后期，试件没有达到历史最大应力水平就已经有较为明显的声发射现象，说明声发射同时存在较为明显的凯塞效应和费利西蒂效应[9]。

4 损伤演化分析及损伤估计模型的确定

4.1 损伤值的计算

Kachanov提出用连续性变量描述金属蠕变断裂过程中其力学性能的连续变化过程，用连续度φ来表示材料损伤因子D，定义损伤连续度φ为材料断面上微缺陷面积SD与无损时断面面积S的比值[10]。即

(1)

之后,唐春安[11]认为材料在破坏过程中产生的声发射事件总数与材料损伤对应一致，利用声发射技术得到的声发射数可以用来估计材料的损伤变量值。在引入微元强度的概率密度函数的基础上假设截面完全劈拉破坏时累计声发射试件总数为Zm，则材料完全破坏时单位面积微元的声发射数为

n=Zm/S。

(2)

则截面破坏面积Ad时，累计声发射数为

Z=nSD=ZmSD/S。

(3)

联立式(2)、式(3)求解，可知声发射数与损伤变量间存在以下关系，即

D=Z/Zm。

(4)

通过基于材料缺陷面积定义的损伤变量与声发射数建立相互关系，而声发射数能反映材料内部损伤变化情况，两者结合起来具有一致性，所以式(4)表明利用声发射技术得到的声发射数可以用来估计材料的损伤变量值。根据上述建立的损伤变量，选取声发射累计撞击数与声发射累计撞击总数的比值来反映混凝土在循环加卸载过程中的损伤程度。损伤变量中各参数的值及混凝土累计残余应变的值详见表1。

表1 不同应变速率时每次循环的损伤值

由表1可知，随着应变速率的提高，混凝土材料从加载到破坏所历经的循环次数逐渐减少，累计撞击总数有数量级的变化。应变速率为10-3/s时，由于声发射探头的掉落，致使采集的累计撞击数不完整，总数相对偏少。

4.2 累计残余应变与循环次数的关系

混凝土残余应变反映的是混凝土在荷载作用下塑性变形和微裂纹的不可恢复程度，在循环加卸载过程中较极限应变更能反映材料本身的特性。在循环加卸载过程中累计残余应变是指每次循环应力卸载到零后对应的应变。对累计残余应变值进行线性回归分析，发现累计残余应变ε与循环加载次数N满足下列关系，即

ε=αNβ。

(5)

式中：α，β为材料参数。拟合参数见表2。由表2可知，公式的拟合度高，能较好地反映累计残余应变与循环加卸载的关系。

表2 累计残余应变与循环加载次数关系的拟合参数

4.3 损伤演化分析

不同应变速率下损伤随累计残余应变的变化规律如图3所示。

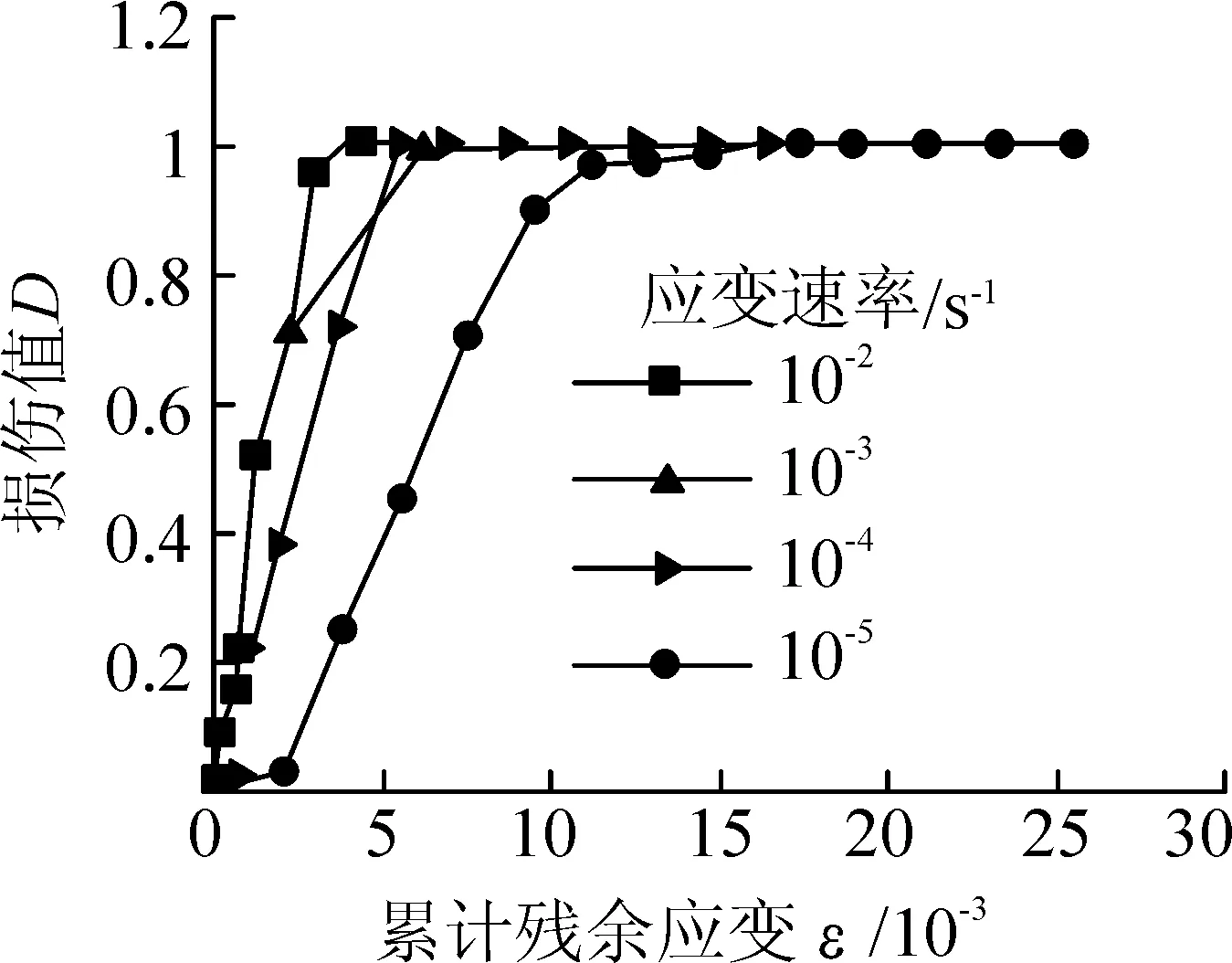
图3 不同应变速率下损伤演化规律

由图3可知，不同应变速率下的混凝土材料在循环荷载作用下损伤曲线形状相似，4种应变速率下混凝土的损伤演化都经历了3个过程，即初始损伤阶段、损伤急剧发展阶段和损伤稳定阶段。在不同的应变速率下，混凝土损伤演化的路径各不相同，但损伤演化的起点与终点是重合的。循环加卸载的过程，实质上就是一个损伤累积与演化的过程，当应变较小时，混凝土前期损伤累积程度较大，后期平缓，出现水平段。随应变速率的提高，损伤累积的路径被大幅度缩减而直接进入破坏阶段。

从不同应变速率下的损伤对比图可以看出，随着应变速率的提高，混凝土损伤演化路径前移，在同等损伤程度下，静载下混凝土所产生的残余变形大，说明试件在受载后变形充分，损伤累计时间长。因而，在同等应力水平下，有静载下混凝土的损伤值明显高于动荷载的。

不同应变速率下的循环加卸载损伤呈“S” 型演化，与混凝土单轴压缩损伤规律有相似性，因而可采用与单轴压缩相似的基于统计理论的概率密度函数来对损伤特性进行研究。首先构建类似的概率密度函数如下：

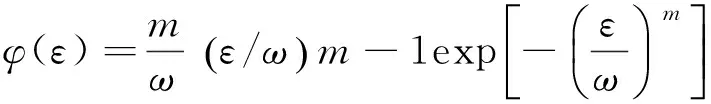
(6)

对式(6)积分再结合式(6)得到

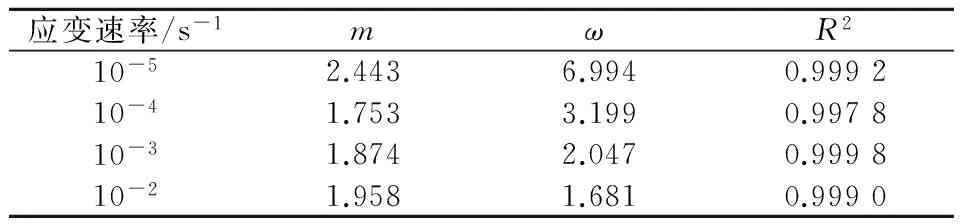
(7)式中：ε为累计残余应变；εp为峰值应变；m，ω为材料均匀参数，通过拟合得到。故现在利用式(7)对4种应变速率下混凝土循环损伤演变规律进行拟合，得到模型中相应的参数，见表3。从拟合效果来看，统计概率密度函数能很好地反映出损伤的演变规律。

由图3可知随着应变速率的提高，混凝土损伤演化路径前移，但是损伤推移量随应变速率的推移值和推移规律未知，现运用构建的损伤模型式(7)对损伤随应变速率的推移规律作进一步分析。图4(a)为不同应变速率下拟合效果组合图，图4(b)为相邻2种不同应变速率下损伤推移值的变化规律图。

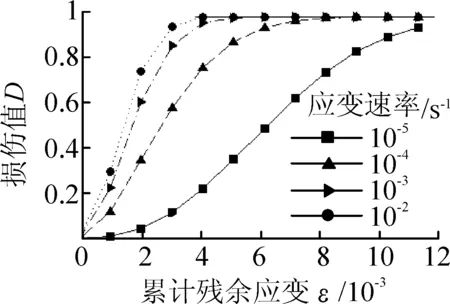
(a)ε-D拟合图

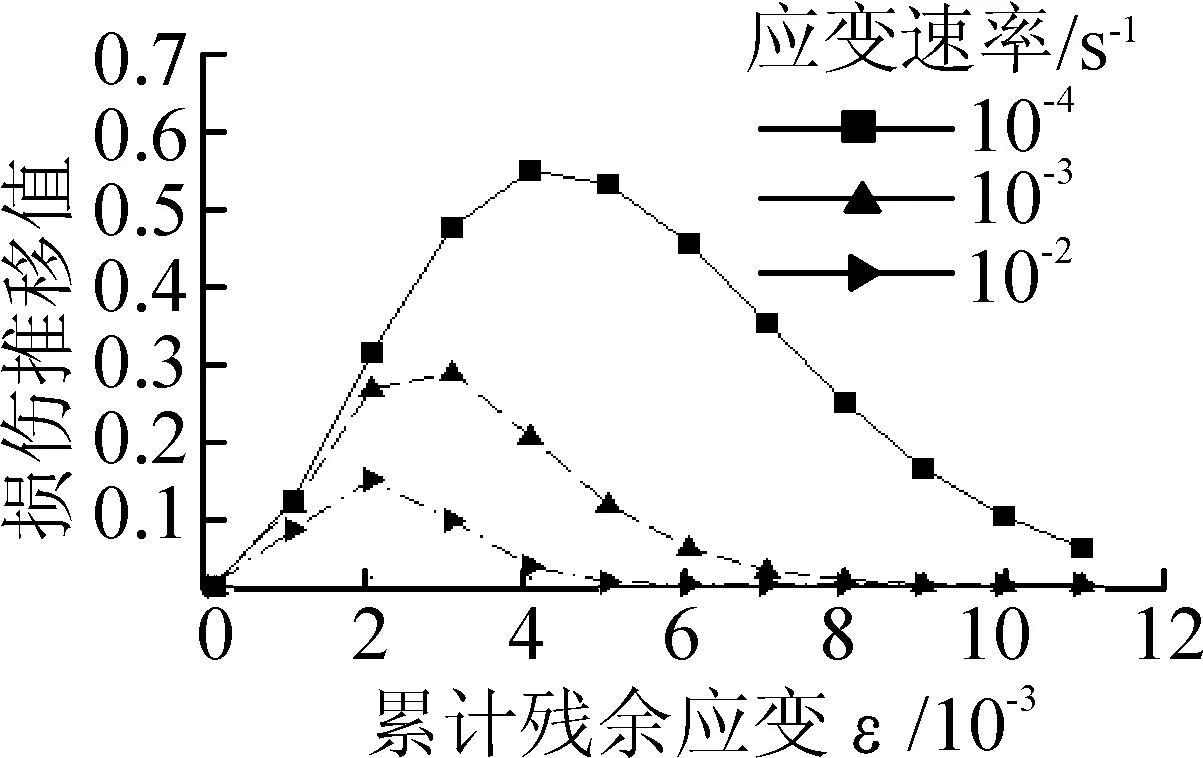
(b)损伤推移值变化规律

当应变速率一定的条件下，后一种应变速率相对于前一应变速率所对应的损伤推移值随着累计残余应变的增大呈现出先增大后减小的规律，当累计残余应变一定的情况下，随着应变速率的提高相邻2种应变速率对应的损伤推移程度在不断减弱。

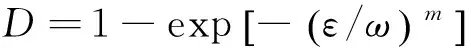
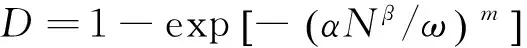
(8)

对式(8)简化得

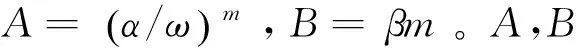
式(9)表明，循环损伤值只与循环次数有关，因此可通过循环次数非常直观的估算循环加卸载的损伤值。

5 结 论

本文对不同应变速率下的循环加卸载声发射信号与应力水平的关系进行了深入分析，建立了基于统计概率密度函数的损伤估计模型，并研究了混凝土在循环荷载作用下的损伤演化规律，主要结论如下：

(1)单个循环加卸载过程中，声发射信号主要出现在加载阶段，在整个循环加卸载试验过程中，声发射信号主要集中在峰值应力以前。随着应变速率的提高，混凝土材料从加载到破坏所历经的循环次数逐渐减少，累计撞击总数有数量级的变化。

(2)在4种不同应变速率下，混凝土损伤演化的路径各不相同，损伤路径随着应变的提高逐渐缩短。随着应变速率的提高，混凝土损伤演化路径前移。

(3)损伤推移值随着累计残余应变的增大呈现出先增大后减小的规律，当累计残余应变一定的情况下，随着应变速率的提高相邻2种应变速率对应的损伤推移程度在不断减弱，统计概率密度函数能很好地反映循环加卸载损伤的演化规律。

[1] 王四巍,高丹盈,刘汉东.循环加卸载下塑性混凝土强度及变形特性[J].工业建筑,2009,(5):92-95.

[2] 石 星,万 玲,邓 涛,等.循环载荷作用下混凝土的压缩特性研究[J].地下空间与工程学报,2008,(4):281-284.

[3] 闫东明,林 皋,王 哲.变幅循环荷载作用下混凝土的单轴拉伸特性[J].水利学报,2005,36(5):593-597.

[4] 梅世强,姜 袁,王乾峰. 循环荷载作用下混凝土卸载刚度试验研究[J].新型建筑材料,2010,(1):1-4.

[5] 胡海蛟,彭 刚,谢玖杨,等.历经循环荷载历史混凝土动态受压试验研究[J].混凝土,2013,(1):51-54.

[6] 关 萍,吴 寅,陈 雄.单轴反复荷载下混凝土动态抗压性能的研究[J].建筑结构学报,2008,(S1):172-175.

[7] 周洪涛. 凝土循环加卸载率效应特性研究[D].宜昌：三峡大学,2013.[8] 李淑春,刁 波,叶英华.反复荷载作用下的混凝土损伤本构模型[J].铁道科学与工程学报,2006,(4)：12-17.[9] 张力伟.混凝土损伤检测声发射技术应用研究[D].大连：大连海事大学,2012.

[10]张 明，李仲奎，杨 强，等.准脆性材料声发射的损伤模型及统计分析[J].岩石力学与工程学报，2006，25(12):2493-2501.

[11]唐春安.岩石破裂过程中的灾变[M].北京：煤炭工业出版社，1993.

(编辑：刘运飞)

Analysis of Dynamic Damage Evolution Translation and a Model ofEstimating Damage Value of Concrete under Cyclic Loading andUnloading

WU Bin1,3, HU Wei-hua2,3, TANG Ke-jing1, WEN Pei-jun4

(1. Department of Architectural Engineering, Hubei Industrial Polytechnic, Shiyan 443000, China; 2. Shiyan Architectural Design Institute, Shiyan 443000 ,China; 3. Hubei Provincial Collaborative Innovation Center for Geo-hazards and Eco-environment in Three Gorges Area, Yichang 443002, China; 4. The First Engineering Co. Ltd. of the 23rd Metallurgical Construction Group, Minmetals, Xiangtan 411100,China)

Concrete samples were tested by multi-function triaxial instrument under cycle load condition with different strain rates. The relationship between acoustic emission signals and stress level was analyzed, and the damage evolution regularity was researched from the aspect of acoustic emission hit number. Furthermore, a single-parameter model that only contains cycle number was established to estimate damage value. The results show that 1) under different strain rates, the paths of damage evolution are not identical. Damage accumulation degree at earlier stage is bigger than that at later stage when the strain is small, and damage curve is flat at later stage; 2) the damage evolution path moves forward with the increase of strain rate, and the value of damage development along with the increase of strain rate presents a regularity that first increases then decreases with the increase of cumulative residual strain. When cumulative residual strain is certain, the damage development degree at two adjacent strain rates weakens with the increase of strain rate; 3) the regularity of concrete damage evolution under cyclic loading and unloading is featured with three phases, which can be reflected by statistical density function.

concrete; cyclic loading and unloading; dynamic damage; acoustic emission; damage variation

2015-08-10;

2015-09-05

吴 彬(1989-)，女，湖北十堰人，硕士研究生，主要从事混凝土材料方面的研究，(电话)18772846370(电子信箱)1660611628@qq.com。

胡伟华(1988-)，男，湖北十堰人，硕士研究生，主要从事结构抗震设计和混凝土材料方面的研究，(电话)18772803749(电子信箱)464913988@qq.com。

10.11988/ckyyb.20150656

2016,33(10):140-144

TU502

A

1001-5485(2016)10-0140-05