梁拱组合桥梁稳定性对于重要设计参数的敏感性研究

鹿立好

(安徽省亳州市恒达公路工程勘察设计院，安徽 亳州 236800)



梁拱组合桥梁稳定性对于重要设计参数的敏感性研究

鹿立好

(安徽省亳州市恒达公路工程勘察设计院，安徽 亳州 236800)

针对矢跨比和拱梁刚度比这两个重要设计参数，研究矢跨比和拱梁刚度比对于梁拱组合体系桥梁稳定性的重要影响，以期为此类桥梁的设计提供参考。

梁拱组合桥；稳定性；矢跨比；拱梁刚度比；敏感度分析

0 引 言

梁拱组合体系桥梁由主梁和拱肋相互协作，共同受力，结合了拱和梁的特点。梁拱组合体系桥梁的矢跨比、梁拱刚度比以及吊杆刚度等重要设计参数对于结构的静力和动力性能影响显著[1-6]。随着桥梁建设水平的不断提高和轻质高强材料的使用，梁拱组合体系桥梁跨径不断增大，结构越来越轻巧、柔和、纤细，使其稳定问题日益突出[7-10]。拱的稳定问题从失稳空间形态上可分为面内失稳和面外失稳；从失稳性质上又可分为第一类稳定(分支点失稳问题)和第二类稳定(极值点失稳问题)。因此，本文将主要针对矢跨比和拱梁刚度比这两个重要设计参数，研究矢跨比和拱梁刚度比对于梁拱组合体系桥梁稳定性的重要影响，为此类桥梁的设计提供参考。

1 桥梁实例

本文选择安徽省广德县境内的广宁路桥作为算例工程(以下简称算例桥梁)，该桥上部结构采用(30 m+80 m+30 m)的梁拱组合体系，主跨采用刚性系杆刚性拱，计算跨径L=80 m，拱轴线为二次抛物线，矢跨比为1/4，矢高为20.0 m，拱肋采用等截面矩形截面，每片拱片设间距为4.0 m的吊杆17根。下部结构桥墩采用实体式墩身下设承台接8根桩基础，桥台采用盖梁接2根桩基础，桩基础直径均为2.2 m，按摩擦桩设计。广宁路桥立面布置图具体见图1所示。

本文采用通用有限元分析软件MIDAS/Civil建立了广宁路桥梁拱组合体系结构的有限元模型，并进行全桥的静力稳定性分析，有限元模型见图2所示。

图2 广宁路桥动力分析有限元模型

2 拱梁刚度比对算例桥梁稳定性的影响

对梁拱组合桥而言，拱肋是主要受力构件之一。在主拱结构的失稳变形过程中，拱肋承担了大部分的变形势能。因此，通过对拱梁刚度比的参数分析，可以了解梁拱组合桥梁拱刚度比的变化对其成桥阶段稳定性的影响。

成桥阶段稳定分析考虑了自重、二期恒载、预应力荷载以及吊杆张力，讨论了不同拱梁刚度比在成桥阶段对稳定性能的影响，计算结果见表1和表2所列。

分析表1和表2可知，算例桥梁在成桥阶段的前三阶失稳模态基本均为主拱的侧倾失稳，这主要是由于拱肋相对于主梁的横向刚度较小，抗侧倾比较薄弱，当荷载达到临界荷载时，首先发生侧倾失稳。需要指出的是，当梁拱刚度比达到4.94时，梁拱组合桥的第三阶失稳模态出现桥面板的局部失稳，由此可见，拱梁刚度比的增加，有可能使局部失稳形式提前。

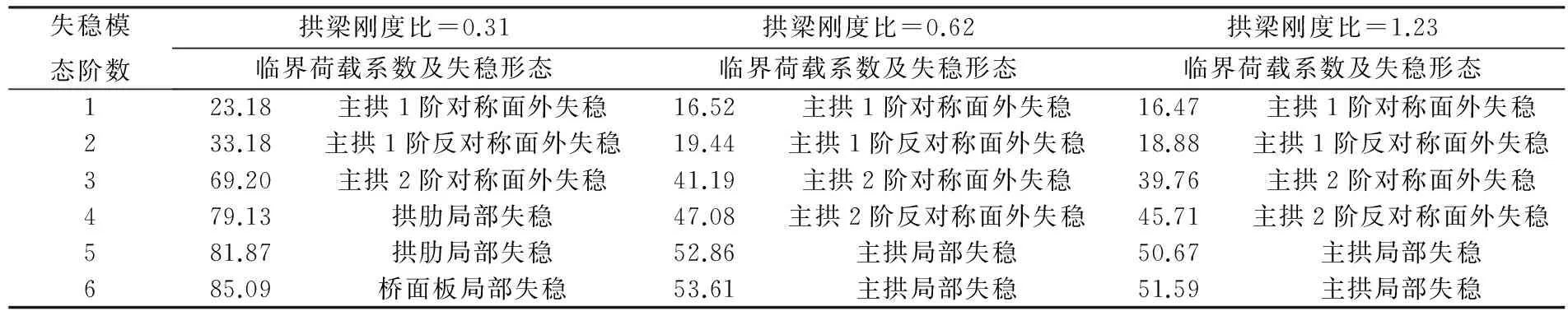
表1 不同拱梁刚度比的临界荷载系数及失稳形态

表2 不同拱梁刚度比的临界荷载系数及失稳形态

分析图3可知结构临界屈曲荷载系数随不同拱梁刚度比的变化规律。随着拱梁刚度比的增加，结构临界屈曲荷载系数(即稳定系数)先减后增，即当拱梁刚度比为0.31时，结构临界屈曲荷载系数为23.18，而当拱梁刚度比为1.23时，结构临界屈曲荷载系数为16.47，结构屈曲荷载系数减小幅度达40.7%；当拱梁刚度比为4.94，结构临界屈曲荷载系数增长较快，后者达前者的2倍之多。由此可见，拱梁刚度比的增加对提高结构安全系数有着重要影响。

图3 拱梁刚度比对结构临界屈曲荷载系数的影响

3 矢跨比对算例桥梁稳定性的影响

矢跨比是决定拱桥线型的重要参数之一，当拱圈跨径和截面一定时，若矢跨比很小，则拱弧长度较短，拱肋的材料用量较小，但均布荷载产生的压力较大；反之，若矢跨比很大，虽压力较小，但拱弧较长，拱肋的材料用量较大。根据拱桥的稳定理论，拱的失稳情况与矢跨比密切相关。下承式拱桥矢跨比多在1/4～1/7之间，因此，本文以算例桥梁为基础，保持拱肋截面形式和拱轴线线型方程表达式不变，分别针对矢跨比为1/4、1/5、1/6、1/7，分析不同矢跨比模型的结构临界屈曲荷载系数，计算结果见表3和表4所列。

分析表3和表4、图4可知，随着矢跨比的增加，结构临界屈曲荷载系数不断增大，当矢跨比为1/7时，结构临界屈曲荷载系数为12.88；而当矢跨比为1/4时，其结构临界屈曲荷载系数为16.47，增幅达27.8%，且随矢跨比的增加，结构失稳模态的方向都朝拱肋的面外失稳，即主拱的面内刚度大于面外刚度。由此可知，通过改变矢跨比，可以增强结构的稳定性。

表3 不同矢跨比的临界荷载系数及失稳形态

表4 不同矢跨比的临界荷载系数及失稳形态

分析图4可知结构临界屈曲荷载系数随不同矢跨比的变化规律。随着矢跨比的增加，结构临界屈曲荷载系数不断提高，这是由于在平衡方程中考虑了轴力对平衡方程的影响。同时，矢跨比和结构临界屈曲荷载系数有呈线性增长的趋势。

图4 矢跨比对结构临界屈曲荷载系数的影响

4 结 论

(1) 随着拱梁刚度比的增加，结构临界屈曲荷载系数(即稳定系数)先减后增；拱梁刚度比的增加对提高结构安全系数具有重要影响。

(2) 随着矢跨比的增加，结构临界屈曲荷载系数不断提高，且矢跨比和结构临界屈曲荷载系数有呈线性增长的趋势。

[1] 于淑兰．梁拱组合桥梁结构体系性能分析[D].大连：大连理工大学，2003.

[2] 王洪超．连续梁拱组合体系桥梁设计参数分析[J].岩土工程界，2006，9(4): 27～29.

[3] 滕丽平．梁拱组合体系桥受力性能研究 [D].长沙：中南林业科技大学,2012.

[4] 易云焜．梁拱组合体系设计理论关键问题研究[D].上海：同济大学, 2007.

[5] 司秀勇,潘慧敏,蒋再松,等. 梁拱组合体系桥自振特性分析及参数研究[J].铁道建筑,2008(1):28～30.

[6] 徐晓东，汪 俊．拱梁组合体系桥梁的结构设计特点[J].交通标准化，2009(21): 27～30.

[7] 李 映．拱梁组合体系桥梁的拱梁相对刚度分析[J].桥梁建设，2008(1):50～53.

[8] 朱卫国，张 松，项贻强．三跨连续梁拱组合体系桥梁稳定性分析[J].中国市政工程，2004，109(3):32～34.

[9] 吴祥海．设计参数对梁拱组合桥稳定性影响研究[J].城市道桥与防洪，2010(9):286～288.

[10] 代 科．梁拱组合体系桥梁的稳定性研究[J].交通世界：建养机械，2011(5):201～203

2016-04-27

鹿立好(1963-)，男，安徽肥西人，安徽省亳州市恒达公路工程勘察设计院高级工程师．

U448.216

A

1673-5781(2016)03-0322-03