基于特征提取的多指标面板数据聚类方法
党耀国,侯荻青
(南京航空航天大学经济与管理学院,南京211106)
基于特征提取的多指标面板数据聚类方法
党耀国,侯荻青
(南京航空航天大学经济与管理学院,南京211106)
多指标面板数据能够较全面的提供研究对象的信息和数据特征,但复杂的数据结构也给其聚类分析带来了一定的困难。针对这一问题,文章提出了基于特征提取的多指标面板数据聚类方法,该方法将能够表征面板数据动态变化的“绝对量”特征、“波动”特征、“偏度”特征、“峰度”特征及“趋势”特征引入动态聚类算法中,可以避免以往采用欧式距离进行聚类的局限性,还可以处理带有缺失数据的面板数据,同时大大提高了聚类效率,并最大限度地保证时间维度信息不受损失。利用该方法分析了2001至2013年我国不同省份道路交通事故的不平衡状况,通过实证分析表明该方法能够解决多指标面板数据聚类的问题。
面板数据;特征提取;动态聚类;交通事故
0 引言
面板数据又称时间序列截面数据或混合数据,是由不同个体在多个时期上观测得到的数据,它综合了时间序列与截面数据的特征,能够描述研究对象的动态特征,在经济与管理问题的建模与分析中具有重要的地位。面板数据的聚类分析是指依据不同指标的观测数据,把数据划分为若干类,以寻找每一类的模式或各种潜在的有用信息,有效的聚类结果还可以作为面板数据计量研究前的预处理步骤,避免仅靠经验分类造成的误差[1]。
本文指出了目前常用的欧式距离在聚类时的缺点,然后提出了一种基于特征提取的面板数据聚类方法:首先从多个角度出发描述面板数据的统计特征,通过提取的特征值构建特征向量来反映面板数据的主要信息,之后通过动态聚类的方法对这些特征进行聚类,以提高聚类效率,并最大限度保证时间维度信息不受损失。
1 面板数据的数据格式及数据特征
1.1单指标面板数据
单指标面板数据是由多个样本在不同时点的指标值构成的数据集合,与截面数据数据格式类似,都可用二维表或矩阵的形式来表示。其聚类分析的思路有两种:第一,将单指标面板数据的时间维度转换为截面数据的指标维度,采用与截面数据完全相同的方法进行聚类;第二,将单指标面板数据的每个样本看做一条时间序列,通过衡量时间序列的相似程度进行聚类。总的来说,单指标面板数据的聚类分析比较简单,聚类方法一般包括系统聚类、动态聚类、灰色聚类等。
1.2多指标面板数据
多指标面板数据从横截面上看,是由若干个体在某一时刻构成的截面观测值,从纵剖面上看则是一组时间序列,其包含的每个数据点可用三下标变量表示,例如,i=1,2,…,N,k=1,2,…,P,t=1,2,…,T。N表示面板数据中含有的个体数;P表示指标变量的总数;T表示时间序列的最大长度。严格来说,多指标面板数据应该以空间三维表的形式来表示,但考虑到面板数据是由不同个体的多个指标随时间变化的序列构成,本文从个体维度将多指标面板数据展开为平面上的二级矩阵,重点从时间维度来设计面板数据的统计量。
样本总体X可表示为矩阵[X1…Xi…XN]T,其中,总体的一个样本Xi的矩阵表示为:
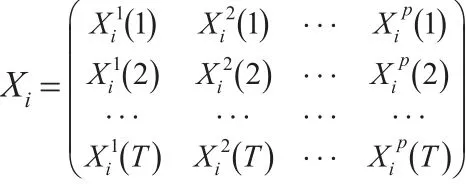
(1)样本i的第k个指标的均值μki
(2)样本i的第k个指标的标准差:
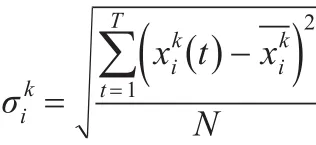
1.3多指标面板数据的时间序列特征
多指标面板数据不仅能反映某一时期指标发展的绝对水平,还能反映其描述的对象在一段时期内的发展趋势、波动程度等动态演化规律。这些特点决定了在对多指标面板数据进行聚类分析时,要综合考虑其时空特征。多指标面板数据的时空特征至少包括以下四方面的信息:(1)某时期指标发展的绝对水平;(2)对某个特定个体而言,某项指标的增长变化情况,即趋势;(3)对某个特定个体而言,某项指标的起伏变化或波动情况;(4)对某个特定个体而言,某项指标的分布特征。
已有文献虽然对面板数据的增量变化进行了一定的讨论,但并未对面板数据的动态变化进行深度挖掘,且计算量异常繁重,使得方法的实用性有所削弱。此外,过去的文献大多采用欧氏距离来刻画面板数据之间的相似性,而欧式距离在处理带有时间序列的数据时存在固有的缺陷。例如,从面板数据中抽取某样本不同指标的两条数据序列与,二者取值时点相同,并且在相同时点上所取的值都相差一个相同的常数,即序列是由向下平移c个单位得到的,两条序列的波动情况完全是相似的,但如果计算欧氏距离,很可能因为两者之间距离过大而得出不属于同一类的结论。
尽管已有一些改进,例如构建反映面板数据波动情况的综合距离,并通过权重的调节来减少上述误差,但是这些改进仍然不支持面板数据可能出现的线性漂移和时间弯曲。如图1所示,两条单指标序列的波形基本相似,但是波峰和波谷的位置并没有完全对齐,而是略有偏差,在欧式距离下这两条时间序列却不会被认为是相似的,这是因为欧式距离只能考察不同样本在对应时点上取值的差异,没有考虑到样本是随时间变化的一列值。
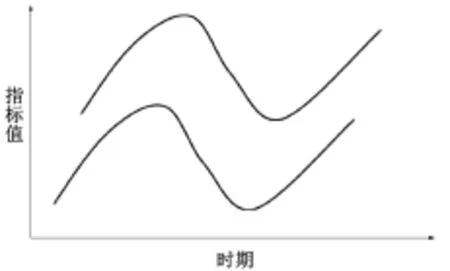
图1 两条单指标序列不同时期的波形
2 面板数据的特征提取
2.1面板数据的标准化处理
由于面板数据的各指标量纲不尽相同或数值范围相差较大,因此需要对进行标准化处理,标准化公式较多,这里采用均值化的方法,即

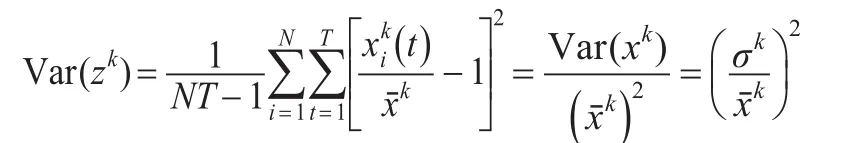
即均值化后各指标的方差是各指标变异系数的平方,这样既消除了量纲和数量级的影响,又可以保留指标值的变异信息,突出后续所提取特征的差异性。为方便表示,下文仍用来表示标准化后得到的
2.2特征提取的基本思想
聚类之前对面板数据进行特征提取,可以揭示其潜在的相似变化机制和结构,从而发现更有意义的聚类结果。本文利用尽可能少的特征来反应面板数据的主要信息,然后再将这些特征进行聚类,可避免上述提到的采用欧式距离进行聚类的缺陷;此外,由于提取的特征来自数据本身,且具有特定的含义,所以最后的聚类结果也具有可解释性。可将基于面板数据的特征提取概括为两个步骤:特征值的计算与特征向量的构建[2,3]。
2.3面板数据特征向量的设计与度量
为了能够准确的刻画面板数据的时空特征,必须考虑指标在考察期内发展的绝对水平、趋势、波动程度、分布情况等,因此,对面板数据聚类的特征向量的设计必须是几方面信息的有效融合。对于面板数据集,设其有N个样品,每个样品有T个时期的P项指标。
定义1样本i的第k个指标的全时“绝对量”特征(AbsoluteQuantity Feature),简记为

定义2样本i的第k个指标的全时“波动”特征(Variance Feature),简记为VF
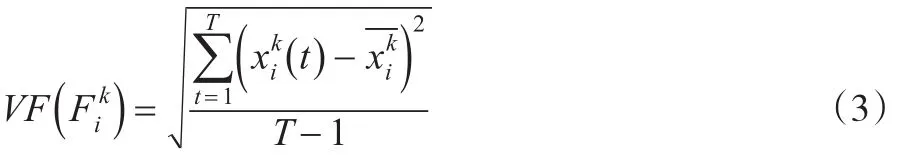
定义3样本i的第k个指标的全时“偏度”特征(SkewnessCoefficientFeature),简记为SCF
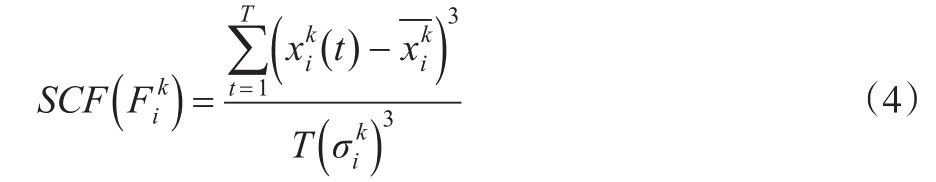
定义4样本i的第k个指标的全时“峰度”特征(KurtosisCoefficientFeature),简记为KCF
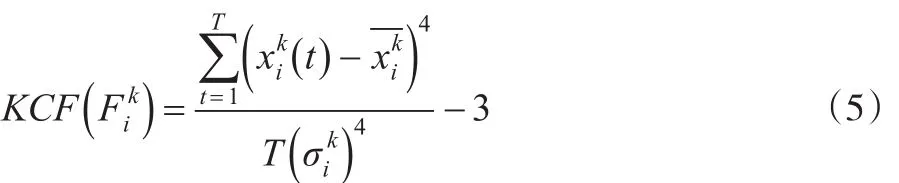
该特征表征了个体i在整个时期T内指标值的集中程度或分布曲线的尖峭程度,若大于0,表示指标值的分布比正态分布更集中在平均值周围;若小于0,表示指标值的分布比正态分布更分散。定义3和定义4都反映了样本数据的分布特征,若两个样本随时间发展呈现较一致的分布,则说明二者更相似。
定义5样本i的第k个指标的全时“趋势”特征(Trend Feature),简记为
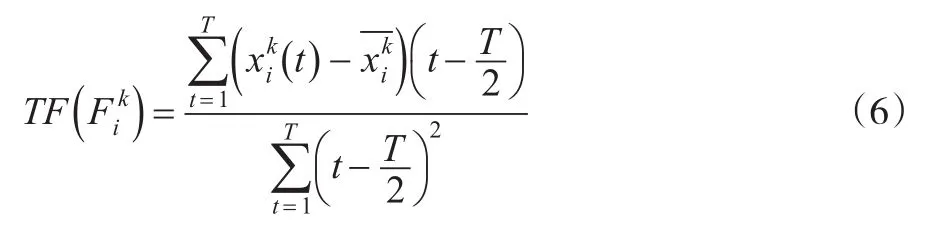
定义6样本i的特征向量(Feature Vector),简记为M i:
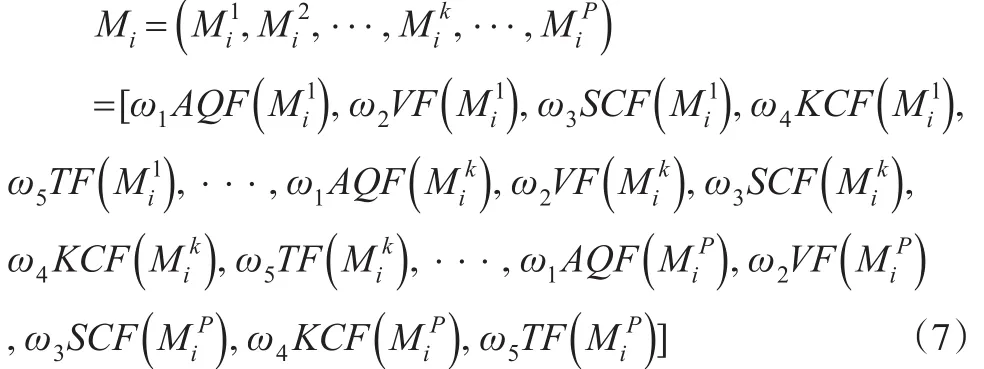
其中
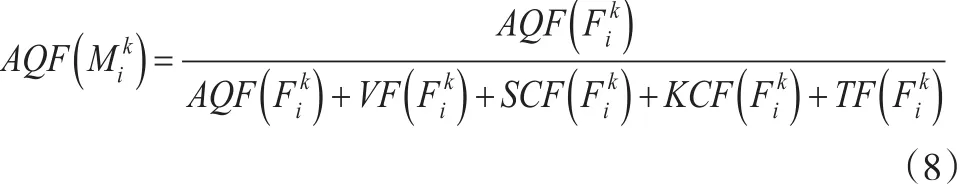
3 聚类方法及聚类步骤
3.1动态聚类分析的基本思想
为了克服系统聚类法效率太低的缺点,就需要避开全面的计算和比较,基于这种思想产生了动态聚类法,又称逐步聚类法。动态聚类法利用迭代法的思想聚类,在局部分析的基础上,作出较为粗略的分类,然后再按某种最优的准则进行修正,直至分类比较合理为止,这样就得到了最终的分类结果。
动态聚类法有许多种方法,目前运用最为普遍的是重心法,又称k均值法,它是麦奎恩(MacQueen)于1967年提出的。这一方法的基本思想是:按照一定的原则,从样本集中选取K个点作为初始聚类中心,记为,括号内序号为迭代次序号;计算各样本点与初始聚类中心的距离D,按照距离最小的原则将样本集分为K类,记为再计算各个类的重心,从而得到新的分类结果重复以上两步,得到分类结果序列给定充分小的允许误差值,当两次分类结果不超过该误差值时,即得到最终分类[4]。
3.2距离的定义
由于聚类算法以距离作为聚集的基础,因此本文采用了标准的欧氏距离来计算类直径以及类之间的距离。对于包含T个时期,P个指标,N个样品的面板数据,我们需要对上文得到的由特征向量Mi表示的不同样本进行聚类,为便于表示,用代替特征向量Mi中的元素,由于向量Mi中包含有P×5个特征值,显然。

这里给出类直径与类间距离的相应公式:
类Gi的直径:
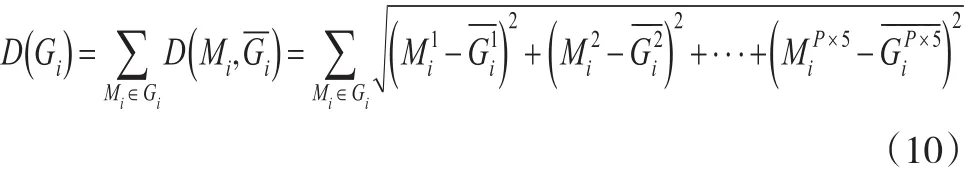
类Gi与类Gj之间的距离:
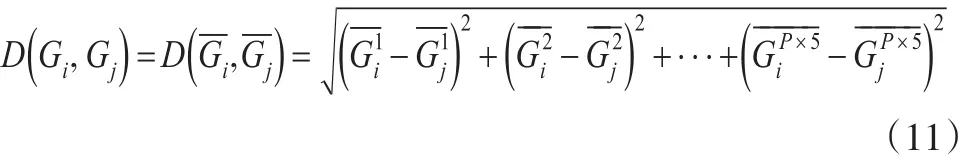
3.3初始聚类数目的确定
需要指出的是,动态聚类法中的聚类数目K需要事先确定。一般来说,聚类数目的增加会导致类内距离下降,类间距离增加,因此,要得到一个绝对最优的聚类数是不可能的。此外,由于经济领域的聚类分析主要用于探索性研究,其分析结果可以存在多个可能解。所以应根据研究目的,针对面板数据的数据信息,并结合所研究问题的实践意义,先初步确定聚类数目的合理区间,进而在上述聚类数目确定方法的基础上,根据实际问题的需要,通过不断筛选和调整,最终获得相对满意的聚类数目,以实现类内相似度和类间相似度二者的协调[5]。
先定义如下函数
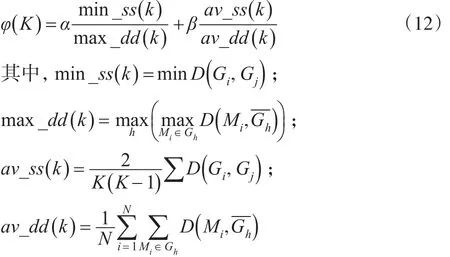
可根据实际情况设定最大和最小的聚类数K1和K2,然后从K1到K2进行聚类计算,从中选取使达到最大的K作为最佳聚类数目。
3.4面板数据动态聚类的步骤
设有N个样品,每个样品有T个时期的P项指标,面板数据动态聚类的具体步骤如下:
步骤2根据式(2)到(6)、(8)分别计算特征值及标准化,根据式(7)得到每个样本的特征值向量Mi,由此构成特征向量集合Ω={Mi| i=1,2,…,N};
步骤3从特征向量集合Ω中选取K个点作为初始聚类中心,记为L(0)={A1(0),A2(0),···,Ak(0)},根据式(10)计算各样本与初始聚类中心的聚类D,若D[Mi,Ah(0)]=min{D[Mi,Aj(0)],∀j=1,2,···,K,j≠i},则判断Mi∈Gh(0),由此把Ω中的向量分为K类,记为Θ(0)={G1(0),G2(0),···,Gk(0)};
步骤6根据式(11)计算各类之间的聚类,得到最终的聚类结果。
4 实证分析
本文对2001年至2013年我国31个省区的交通事故情况进行聚类分析,呈现了我国地区间交通事故的不平衡状况,并对造成这种差异性的可能原因进行了分析。
4.1数据来源和处理方法
本文选取交通事故次数、死亡人数、受伤人数以及直接经济损失这四个指标来考察我国的交通事故情况。该四项指标既是认识交通事故的起点,又是构造其他交通事故统计指标的基础,基本涵盖了道路交通事故所造成各种损害的主要方面,表征的交通事故情况直观、明确,在交通事故统计分析中具有重要意义。本文使用的数据来源于中国统计年鉴(2002年-2014年)。
4.2聚类分析结果
按照前文提出的面板数据聚类方法与步骤,借助SPSS19与EXCEL2007运算工具对各省交通事故数据进行了聚类。为了对聚类结果进行对比分析,本文分别计算了特征向量取不同权重时的聚类结果,见表1。显然,可以看出,不同权重系数确定的分类结果存在一定的差异,一般来说,某个特征值的权重系数越大,最终的聚类结果越能反映该方面的特点。对权重向量W1、W2、W3的赋值分别侧重于反映面板数据的绝对量、长期趋势及发展波动情况。例如,在权重W=(0,0.25,0.25,0.25,0.25)时,上海、江苏、浙江、福建、山东、河南、广东被聚为一类,这几个省份每年交通事故的指标值有较大差异,但波动情况十分相似,各项指标几乎同时在2002年达到最大值,之后快速下降,这与2003年《道路交通安全法》的出台应该存在直接的关系,说明该法的颁布实施对这些地区维护交通安全和预防交通事故,起到了至关重要的作用。
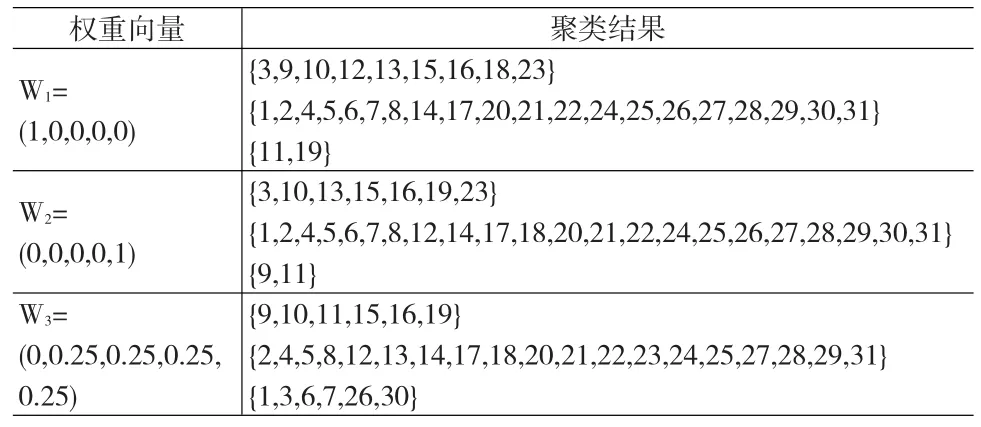
表1 不同权重下交通事故的面板数据聚类结果
本文在专家调查的基础上,通过AHP法得到了面板数据5个特征的主观权重系数,即:W=(0.375,0.125,0.1,0.1, 0.3),此权重系数表明:决策者最看重的是中国交通事故发展的绝对量特征,其次是趋势特征,此时31个省的交通事故状况被分为三类。
第一类包括北京、天津、山西、内蒙古、辽宁、吉林、黑龙江、安徽、江西、湖北、湖南、广西、海南、重庆、贵州、云南、西藏、陕西、甘肃、青海、宁夏、新疆,多为西南和东北地区,这些地区地域广阔、人口密度低、经济相对落后,道路的技术等级和通达性总体较差,交通机动化程度和运输规模均很低,交通安全状况相对较好,但北京和天津为例外;第二类包括河北、上海、江苏、福建、山东、河南、四川,这些地区作为全国社会经济发展的中间带,交通安全状况一般;第三类包括浙江、广东,由于社会经济活跃、人口总量大,不仅道路条件好,而且机动化程度高、交通运输规模和道路通行率很大,所以交通状况最差,各项指标值都远高于其他各省。
经济发展必然依赖并带动人员出行和物资流通,从而导致交通运输规模的扩张,因此,经济的发展在初期会导致交通事故的增加;但随着经济的进一步发展,为交通建设提供了财力保障,政府和社会也会更加重视交通安全,积极加强交通管理和行为规范,从而有利于降低车辆的事故率[6,7]。这就解释了为什么北京市和天津市的经济发达程度明显优于其他各省,但交通安全状况却较好。另一方面,浙江和广东虽然经济发达程度也很高,但本身常住人口密度大,且外来务工人员多,流动性大,无形中增加了交通管制的难度,但交通规模扩大后的交通冲突增加,仍会使事故的总量提高,所以交通事故的各项指标值都位于各省前列,交通安全形势依然严峻。
5 结束语
本文聚类方法适用于多指标面板数据的样本分类问题,综合考虑多指标面板数据的动态特征,提出了用“绝对量”特征、“波动”特征、“偏度”特征、“峰度”特征、“趋势”特征来表征多指标面板数据,并在此基础上提出了多指标面板数据的动态聚类方法,利用该方法分析了2001至2013年我国不同省份道路交通事故的不平衡状况,通过实证分析表明该方法能够解决多指标面板数据聚类的问题。需要指出的是,本文中的特征提取思想实际上是一种数据的压缩处理,势必会造成部分信息的损失,因此仅适用于具有较长时间维度的面板数据的聚类(T≥10);此外,本文仅仅构造了几个基础性的特征统计量来反映经济管理中面板数据的动态特征,其他更深层次更复杂的特征统计量还有待进一步研究。
[1]刘文丽,郝万禄,夏球.我国科技金融对经济增长影响的区域差异——基于东部、中部和西部面板数据的实证分析[J].宏观经济研究,2014,(02).
[2]Wang X,Wirth A,Wang L.Structure-based Statistical Features and Multivariate Time Series Clustering[R].Proceedings of the Seventh IEEE InternationalConferenceon DataMining,2007.
[3]宋辞,裴韬.基于特征的时间序列聚类方法研究进展[J].地理科学进展,2012,10(31)
[4]徐华锋,方志耕.面板数据聚类分析的投影寻踪模型[J].统计与决策,2010,(04).
[5]卞亦文.大样本数据聚类的改进方法[J].统计与决策,2009(01).
[6]王明霞.道路交通安全与社会经济影响因素的综合关联分析[J].管理世界,2011(03).
[7]王洪明.我国区域道路交通安全形势对比与影响因素分析[J].中国安全科学学报,2010,(06).
(责任编辑/易永生)
0212,C812
A
1002-6487(2016)19-0068-05
国家自然科学基金资助项目(71071077,71371098);中央高校基本科研业务费专项资金资助项目(NC2012001);南京航空航天大学基本科研业务费专项科研资助项目(NZ2010006)
党耀国(1964—),男,江苏南京人,教授,博士生导师,研究方向:灰色系统理论、数量经济。

