基于ARIMA-ERNN组合模型预测我国甲肝发病率*

许春杰，尹素凤，郭春月，宋瑞瑞，汪可可，肖孟迎，张秀峰，刘晓宇，范红敏，冯福民，

胡 泊1)#



基于ARIMA-ERNN组合模型预测我国甲肝发病率*

许春杰1)，尹素凤1)，郭春月1)，宋瑞瑞1)，汪可可1)，肖孟迎1)，张秀峰1)，刘晓宇2)，范红敏1)，冯福民1)，

胡 泊1)#

1)华北理工大学公共卫生学院医学统计与流行病学系 唐山 063000 2)华北理工大学附属开滦医院呼吸内科 唐山 063000

#通信作者,男，1976年5月生，博士，副教授，研究方向：流行病与卫生统计学，E-mail：lxy_hb007@126.com

ARIMA模型；BPNN模型；ERNN模型；组合模型；甲肝；发病率；预测

目的：比较ARIMA模型、BPNN模型和ARIMA-ERNN组合模型在我国甲肝发病率预测中的应用效果，探讨预测甲肝发病率的优化模型。方法：收集2004年1月至2015年12月我国甲肝发病率资料，用SPSS 17.0和Eviews 8.0建立ARIMA模型，用Matlab 8.0建立BPNN模型和ARIMA-ERNN组合模型，并对模型的预测效果进行评价。结果：ARIMA-ERNN组合模型拟合及预测的MRE、MER、MSE、RMSE、MAE均小于ARIMA模型和BPNN模型，其MRE均小于5%。结论：ARIMA-ERNN组合模型对我国甲肝发病率的拟合及预测效果优于ARIMA模型和BPNN模型。

甲肝是一种容易造成大流行的传染病，因此基于模型探讨甲肝的流行趋势及流行规律，对于探索甲肝的病因线索，制定相应的预防策略及措施具有非常重要的作用。目前用于预测传染病发病的方法主要有季节性自回归滑动平均混合模型(autoregressive integrated moving average model，ARIMA)、反向传播网络(back-propagation network，BPNN)、残差自回归模型和灰色模型等[1-6]。由于传染病的发病受到很多因素的制约，其中包含许多不确定因素，故其变化趋势呈现出复杂的非线性变化特征。单一的线性模型和非线性模型皆存在信息源不广泛问题，因此在应用中常常受到限制或达不到高精度的要求[7]。组合预测就是将不同的单一预测模型按一定方式进行组合，综合利用各种方法所能够提供的信息，取长补短，优势互补，从而达到提高预测精度和增加预测稳定性的效果[8]。Elman神经网络(Elman neural network，ERNN)是一种非线性反馈型神经网络模型，它在前馈网络的隐含层中增加一个承接层，可以使系统具有适应时变特性的能力，且有非常强的非线性逼近和忽略外部噪声影响的能力，特别适用于解决时间序列问题[9]。该研究利用我国2004至2014年甲肝发病率序列建立ARIMA-ERNN组合模型，并比较该组合模型、ARIMA模型和BPNN模型对2015年甲肝发病率预测的准确性，以探讨预测甲肝发病率的优化模型。

1 资料与方法

1.1 资料 2004年1月至2015年12月甲肝发病资料来源于中国疾病预防控制中心传染病直报系统，人口资料来源于中国卫生统计局。以2004至2014年数据建模。

1.2 ARIMA模型[1,9-10]通过单位根检验确定序列是否为平稳序列，对于非平稳序列通过对数转换和差分的方式来消除季节和趋势的影响，从而获得平稳的时间序列；以赤池信息准则(AIC)和Schwarz贝叶斯准则(SBC)最小、对数似然函数值(Log likelihood)最大的模型为最优ARIMA模型；模型诊断时残差序列应是白噪声，其自相关系数(ACF)和偏自相关系数(PACF)不应与0有显著的差异，Box-LjungQ统计量应无统计学意义，且模型各系数估计值均应有统计学意义。ARIMA模型公式如下：

Ф(B)Ф(Bs) ▽d▽SDXt= θ(B)Θ(Bs)εt；

E(εt)=0，var(εt)= σ2，E(εtεs)=0，

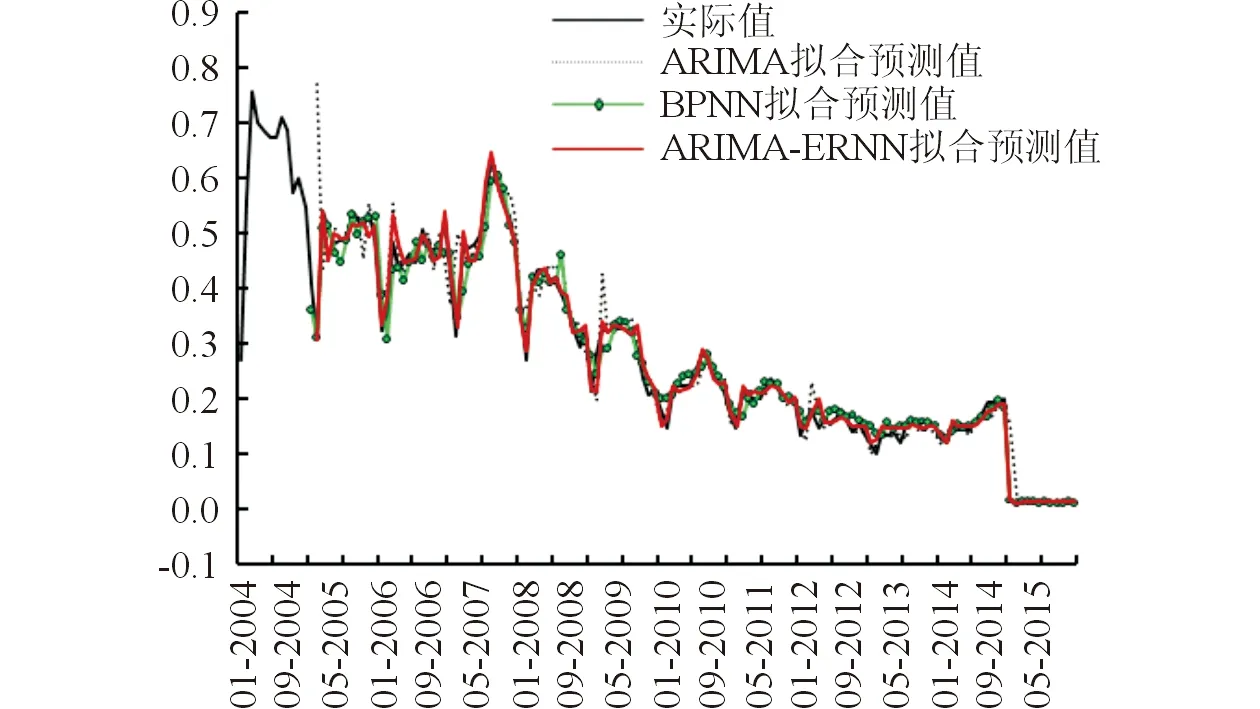
s≠t E(xtεt)=0，∨s

公式中，B为后移算子，εt为残差，d和D分别为非季节和季节差分次数，p和q分别为自回归和滑动平均阶数，P和Q分别为季节自回归和滑动平均阶数；▽d=(1-B)d；▽SD=(1-B)SD；Ф(B)=1-Ф1B-…ФpBp；θ(B)=1-θ1B-…θqBq；Ф(Bs)=1-Ф1Bs-…ФPBPs；Θ(Bs)=1-Θ1Bs-…ΘQBQs。

1.3 BPNN模型[2,7]BPNN模型是多层感知器中的一种“逆推”学习算法，网络结构由输入层、隐含层及输出层组成；其学习过程正向传播时，输入信息由输入层经过隐含层处理传向输出层，若输出层结果超过期望误差，则转入第二阶段的反向传播过程，即将误差信号沿原来的连接通路逐层向输入层反传，通过修改各层节点间的连接权重值，反复调整网络参数，将误差分摊给各层所有单元，最终使得误差信号最小。BPNN模型的建模过程分为三步：①采用newff函数实现网络的生成及初始化。②采用train函数对网络进行训练。③利用sim函数对网络进行仿真。

1.4 ARIMA-ERNN组合模型[11]ERNN模型是在BPNN模型的基础上，通过承接层将隐含层的输出自联到隐含层的输入。这种方式使得ERNN模型对历史状态的数据具有敏感性，内部反馈网络的加入增加了网络本身处理动态信息的能力，从而达到了动态建模的目的。通过甲肝发病率序列建立ARIMA模型，由于甲肝发病率序列的ARIMA模型拟合值与实际值存在高度的关联性，可以将ARIMA模型拟合值作为ERNN模型的输入，以甲肝发病率序列的实际值作为ERNN模型的输出，通过newelm函数构建一个一维输入、一维输出的优化ERNN模型。

1.5 模型预测效果比较 用所建立的模型预测2015年甲肝发病率，并与实际值比较。模型评价指标包括相对误差(RE)，平均相对误差(MRE)，平均误差率(MER)，均方误差(MSE)，均方根误差(RMSE)和平均绝对误差(MAE)[7]。

1.6 统计学处理 使用SPSS 17.0和Eviews 8.0建立ARIMA模型，使用Matlab 8.0建立BPNN和ARIMA-BPNN组合模型。

2 结果

2.1 ARIMA模型结果 利用Eviews 8.0进行单位根检验，单位根ADF=-1.836 1，P=0.364 2，提示我国甲肝发病率序列为非平稳序列。所以首先对原始序列进行对数转换和D=1的季节差分、d=1的非季节差分来消除季节和趋势的影响，以获得稳定的方差和均值，从而获得平稳序列。再结合经过对数转换和季节差分的ACF和PACF图、残差情况，以及系数之间的相关性选取最优模型。通过比较并结合模型简洁的原则，得到的最优模型是ARIMA(1,1,0)×(0,1,1)12，具体方程为(1-B)(1-B12)Xt=(1-0.739B12)εt/(1+0.445B)。其残差的ACF和PACF图，见图1，非季节性自回归系数AR1=-0.445 (t=-4.384，P<0.001)，季节性滑动平均系数SMA1=0.739(t=4.013，P<0.001)，AIC=-0.211，SBC=8.415，Log likelihood=82.477。残差序列Box-LjungQ=10.753，P=0.770，提示残差序列是白噪声。利用建立好的模型预测2015年甲肝发病率，预测值见表1第3列。

图1 ARIMA(1,1,0)×(0,1,1)12模型残差序列的ACF和PACF图表1 2015年甲肝发病率(1/10万)3种模型的预测值

月份实际值ARIMA模型预测值RE/%BPNN模型预测值RE/%ARIMA-ERNN组合模型预测值RE/%10.0180.15716.6670.0175.5560.0175.55620.0120.01716.6670.0120.0000.0118.33330.0150.0166.6670.0146.6670.0150.00040.0140.0140.0000.0157.1430.0137.14350.0130.0147.6920.0147.6920.0130.00060.0130.0127.6920.0130.0000.0130.00070.0150.0146.6670.0150.0000.0150.00080.0140.01614.2860.0137.1430.0137.14390.0150.0146.6670.01313.3330.0146.667100.0140.0140.0000.0137.1430.0137.143110.0140.0140.0000.0140.0000.0140.000120.0140.0140.0000.0137.1430.0140.000

2.2 BPNN模型结果 由于甲肝发病率变化的周期为年，因此BPNN模型输入层和输出层神经元个数分别为12和1，隐含层神经元个数根据经验公式[11]取5～14。因此以5～14作为隐含层神经元个数分别对2004至2014年甲肝发病率进行训练，训练目标误差为0.001，训练步数为2 000。隐含层神经元的传递函数为tansig，输出层为logsig，采用函数trainlm对网络进行训练。在经过2 000次训练后，当隐含层神经元个数为5～14时，网络的逼近误差

(RES)分别为0.625 971、0.624 133、0.567 506、0.243 915、0.400 129、0.462 395、0.466 427、0.493 232、0.496 538、0.507 333。可见当隐含层神经元为8时网络训练误差最小，神经网络对函数的逼近效果最好，而且经过12次训练即可达到目标误差的要求(训练的MSE=0.000 891)。因此选择12-8-1作为最优BPNN模型，利用该模型预测2015年甲肝发病率，预测值见表1第5列。

2.3 ARIMA-ERNN组合模型结果 对甲肝原始序列进行D=1的季节差分和d=1的非季节差分导致13个数据损失，因此以2005年2月至2014年12月ARIMA模型的拟合值作为ERNN模型的输入值，以对应月份的甲肝实际发病率作为ERNN模型的输出值。网络输入层和输出层神经元个数均为1。为防止过拟合，隐含层神经元个数采用试凑法在1～15之间寻找。网络训练函数及权值的修正函数分别采用traingdx和learngdm，其余参数设置同BPNN模型。隐含层神经元个数为1～15时网络的RES和MSE见表2。表2提示，当隐含层神经元个数为11的时候，RES和MSE最小，而且经过98次训练就达到了目标误差的要求。因此选择隐含层神经元个数为11。用确定好的网络构建ARIMA-ERNN组合模型。以2015年ARIMA模型的预测值为输入值，用组合模型对2015年甲肝的发病率进行预测，预测值见表1第7列。

表2 不同隐含层神经元个数对应的网络训练误差

2.4 3种模型性能比较 3种模型对甲肝发病率的拟合及预测效果见表3。由表3可知，ARIMA-ERNN组合模型的拟合及预测性能均优于ARIMA模型和BPNN模型。图2为3种模型对甲肝发病率的拟合及预测曲线，提示ARIMA-ERNN组合模型的拟合及预测曲线与原始值最接近。

表3 3种方法对甲肝发病率的拟合及预测效果比较

图2 3种模型拟合及预测的甲肝发病率曲线

3 讨论

我国甲肝的发病率数据序列中既有线性成分又有非线性成分，同时具有动态性的特点，因此该研究建立了具有ARIMA模型和ERNN模型优点的ARIMA-ERNN组合模型，并用其对我国甲肝发病率进行了预测。有文献[4，12-13]报道模型拟合及预测的MRE小于10%时预测效果较好，小于5%时预测的准确度和精度最佳。该研究中ARIMA模型和BPNN模型拟合及预测的MRE均小于10%，说明其有较佳的预测效果，但其拟合及预测精度均低于ARIMA-ERNN组合模型， ARIMA-ERNN组合模型拟合和预测的MRE均小于5%，表明ARIMA-ERNN组合模型拟合及预测效果优于ARIMA模型和BPNN模型。ARIMA-ERNN组合模型拟合及预测值对我国甲肝发病原始序列进行了很好的跟踪，提示ARIMA-ERNN组合模型能更好地反映我国甲肝发病率序列的内部规律和未来趋势。

需注意的是BPNN模型和ARIMA-ERNN组合模型建模过程中对网络结构的确定是关键：①隐含层神经元个数的确定尚无理论上的指导，如果隐含层神经元个数太少，网络不能反映时间序列的内部规律；若隐含层神经元太多，会导致网络训练和学习时间过长，泛化能力降低等，因此需要通过对网络进行多次反复训练以寻找到最佳的隐含层神经元个数。该研究根据经验，以网络逼近误差和MSE为评价指标，确定了最佳的隐含层神经元个数。②网络初始化权重和阈值是随机生成的，因此每一次网络训练结果都是不一样的。该研究使用循环控制语句对网络进行多次反复训练，找出最佳的一次训练结果，用命令save保存网络，预测时使用命令load调用，这样可使预测结果不会发生变化。③ARIMA-ERNN组合模型的训练函数通常采用traingdx，这样不但可以提高网络的训练效率，还可以有效地抑制局部极小值的出现，而trainlm函数的训练速度太快，在ERNN模型中性能并不是很好[11]。

目前已有相关研究[8,14-16]将ARIMA-ARCHA、ARIMA-GRNN和ARIMA-NARNN组合模型应用于传染病发病率的预测，研究结果表明它们的拟合及预测效果优于ARIMA模型，且ARIMA-NARNN组合模型拟合及预测性能优于ARIMA-GRNN组合模型。因此下一步可考虑将ARIMA-ERNN组合模型的拟合及预测效果与上述几个组合模型进行比较，寻找预测我国甲肝发病的最佳组合模型。

综上所述，ARIMA-ERNN组合模型在一定程度上具有较高的预测精度与准确度，因此可借助ARIMA-ERNN组合模型对我国甲肝发病率进行早期预警，为我国甲肝的防控工作提供参考依据，从而减少或者消除决策的盲目性[9]。但在实际工作中应用组合模型时需注意：①在满足模型使用条件的情况下，根据数据序列的特征，选择合适的单项模型进行组合预测，否则模型的效能不但得不到提高，反而会提供一些不正确的信息。②传染病发病是多因素综合作用的结果，在条件允许的情况下，尽可能多地收集影响传染病发生的因素来构建组合模型。③单次分析构建的组合模型，只适用于短期预测。在实际应用过程中，应不断收集新的数据序列对已建立的模型进行外回代验证[13]，以建立更能反映时间序列的内部规律和未来趋势的组合模型。

[1]王永斌,郑瑶,柴峰,等.基于周期分解的ARIMA模型在甲肝发病率预测中的应用[J].现代预防医学,2015,42(23):4225

[2]GUAN P,HUANG DS,ZHOU BS.Forecasting model for the incidence of hepatitis A based on artificial neural network[J].World J Gastroenterol,2004,10(24):3579

[3]WEI J,HANSEN A,LIU Q,et al.The effect of meteorological variables on the transmission of hand, foot and mouth disease in four major cities of Shanxi province, China: a time series data analysis(2009-2013)[J].PLoS Negl Trop Dis,2015,9(3):e0003572

[4]GUO X,LIU S,WU L,et al.Application of a novel grey self-memory coupling model to forecast the incidence rates of two notifiable diseases in China: dysentery and gonorrhea[J].PLoS One,2014,9(12):e115664

[5]万燕丽，杨永利，施念，等.ARIMA模型在河南省AIDS疫情预测中的应用[J].郑州大学学报(医学版)，2015,50(2)：160

[6]陈银苹，吴爱萍，余亮科.组合模型对乙肝发病趋势的预测研究[J].解放军医学杂志，2014,39(1)：52

[7]ZHANG X,LIU Y,YANG M,et al.Comparative study of four time series methods in forecasting typhoid fever incidence in China[J].PLoS One,2013,8(5):e63116

[8]YAN W,XU Y,YANG X,et al.A hybrid model for short-term bacillary dysentery prediction in Yichang City, China[J].Jpn J Infect Dis,2010,63(4):264

[9]LIU L,LUAN RS,YIN F,et al.Predicting the incidence of hand, foot and mouth disease in Sichuan province, China using the ARIMA model[J].Epidemiol Infect,2016,144(1):144

[10]朱玉,夏结来,王静.单纯ARIMA模型和ARIMA-GRNN组合模型在猩红热发病率中的预测效果比较[J].中华流行病学杂志,2009,30(9):964

[11]葛哲学.神经网络理论与MATLABR2007实现[M].北京:电子工业出版社,2007:111

[12]ZHOU LL,YU LJ,WANG Y,et al.A hybrid model for predicting the prevalence of schistosomiasis in humans of Qianjiang City,China[J].PLoS One,2014,9(8):e104875

[13]王永斌,柴峰,李向文,等.ARIMA模型与残差自回归模型在手足口病发病率预测中的应用[J].中华疾病控制杂志,2016,20(3):303

[14]WU W,GUO J,AN S,et al.Comparison of two hybrid models for forecasting the incidence of hemorrhagic fever with renal syndrome in Jiangsu Province, China[J].PLoS One,2015,10(8):e0135492

[15]ZHANG G,HUANG S,DUAN Q,et al.Application of a hybrid model for predicting the incidence of tuberculosis in Hubei, China[J].PLoS One,2013,8(11):e80969

[16]ZHENG YL,ZHANG LP,ZHANG XL,et al.Forecast model analysis for the morbidity of tuberculosis in Xinjiang, China[J].PLoS One,2015,10(3):e0116832

(2016-01-22收稿 责任编辑王 曼)

Forecasting incidence of hepatitis A based on ARIMA-ERNN combination model in China

XUChunjie1),YINSufeng1),GUOChunyue1),SONGRuirui1),WANGKeke1),XIAOMengying1),ZHANGXiufeng1),LIUXiaoyu2),FANHongmin1),FENGFumin1),HUBo1)

1)DepartmentofEpidemiologyandBiostatistics,SchoolofPublicHealth,NorthChinaUniversityofScienceandTechnology,Tangshan063000 2)RespiratoryMedicine,KailuanHospital,NorthChinaUniversityofScienceandTechnology,Tangshan063000

ARIMA model;BPNN model;ERNN model;combination model;hepatitis A;incidence;forecasting

Aim: To compare the effect of ARIMA model, BPNN model and ARIMA-ERNN combination model in prediction on incidence of hepatitis A in China, and compare the predictive effect among them. Methods: The data of incidence of hepatitis A from January 2004 to December 2015 in China were collected and SPSS 17.0 and Eviews 8.0 were used to construct ARIMA model, Matlab 8.0 was used to establish BPNN model and ARIMA-ERNN combination model. At the same time, the data in 2015 was used to evaluate the effect of prediction. Results: The MRE, MER, MSE，RMSE,MAE fitted and forecasted by ARIMA-ERNN combination model were lower than those of ARIMA model and BPNN model,and the MRE was lower than 5%.Conclusion: The ARIMA-ERNN combination model for forecasting the incidence of hepatitis A is superior to the single ARIMA model and BPNN model.

10.13705/j.issn.1671-6825.2016.06.010

*河北省卫生厅医学科学研究重点课题计划 20130055;华北理工大学培育基金项目 SP:201505

R512.601