结合Craig插值分析的软件错误诊断方法

徐 勇,毋国庆,袁梦霆

(1.武汉大学计算机学院,湖北武汉 430072；2.广东肇庆学院数学与统计学院,广东肇庆526061)



结合Craig插值分析的软件错误诊断方法

徐 勇1,2,毋国庆1,袁梦霆1

(1.武汉大学计算机学院,湖北武汉 430072；2.广东肇庆学院数学与统计学院,广东肇庆526061)

基于模型诊断(MBD)的理论应用到软件错误定位中取得了一定的效果.但是经典MBD理论基于元件间独立地发生故障这一假设,导致软件错误定位的结果中存在假阳性的诊断.论文对现有基于MBD 的软件错误定位方法进行了改进,提出了冲突中元件的冗余分析方法.该方法既包括了基于Craig插值的元件冗余分析机制,同时利用条件语句取值的二元性(真或假)的特点,对冲突中的条件语句元件进行软件错误的无相关分析.实验结果表明:冲突中的元件冗余分析方法可以有效地减少诊断的假阳性率,将诊断结果数减少了48.4%,碰集树生成的结点数减少了47.6%.

基于模型诊断；软件错误定位；冗余分析；Craig 插值

1 引言

软件错误定位是软件调试的第一步,其任务是找出软件中引发软件失效的程序部分.软件错误定位费时、费力.研究开发自动或半自动的软件错误定位方法一直是学术界关注的热点课题.

近年来的文献资料显示,人们对于自动软件错误定位方法展开了大量而深入的研究[1-5].在这些研究工作中,其采用的技术方法主要可分以下几类:(1) 基于频谱的错误定位方法[1-2]；(2) 基于模型诊断(Model-Based Diagnosis)的软件错误定位方法[3,4]；(3) 基于概率统计方法的软件错误定位[5].当然,也有将值替换[6],状态比较[7],程序不变式[8],测试用例分析[9]等应用到软件错误定位中.本文关注的是基于MBD的软件错误定位.

针对电器元件中的故障诊断问题,Retier[10]提出MBD理论和诊断方法.其基本思想是,用合适的逻辑(例如一阶逻辑等)构造系统的行为和结构模型,通过系统运行行为与系统预期行为之间的不一致的观察,结合逻辑的推理功能推导出哪个或哪些元件引发了系统工作异常；诊断的计算依赖于冲突集及碰集树(Hit Set Tree)的构造,每一个诊断都是冲突集的最小碰集.如果将程序中的语句视为MBD中的元件,可以将 MBD应用于软件的错误定位[11-13].但是程序中的语句之间往往存在着数据及控制依赖关系,而Reiter在其MBD理论中假设了系统中的元件独立地发生功能故障.因此,直接应用MBD到软件的错误定位而不考虑元件之间存在的依赖关系将会影响错误诊断的准确性,即候选诊断中存在假阳性.

Birgit Hofer[13]等人提出应用程序切片获得语句间的依赖关系,并与MBD相结合提高诊断结果的质量.Jorg Weber[14]等人则提出增加元件依赖关系模型来表达元件之间可能发生故障的关系,从而支持对元件依赖性故障和独立性故障的诊断.MBD中冲突的存在是系统中的元件集导致系统的行为模型与实际行为的不一致,也即是逻辑上的不可满足.Craig插值提供了一种更简单的形式展示不可满足公式的原因[15].借助Craig插值,可以分析出冲突中的元件在系统行为模型逻辑上不可满足的作用,从而识别出冗余元件.与此同时,程序中条件语句的取值无非是真和假.而给定一个具体失败输入,其只可能执行程序的某一条路径.如果冲突中的条件语句元件无论是取真或假值,系统的合法行为模型仍不可满足,则表明冲突中的条件语句元件与当前失败输入所引发的软件失效是不相关的.事实上,文献中既有利用Craig插值对不可满足的逻辑公式进行化简分析的成功应用[16-17],也有利用分支条件语句取值二元性的特点进行程序错误定位[18-19],这些都启发我们在MBD框架下存在进行冲突中元件不相关分析的可能性.

2 基于MBD的软件错误定位

2.1 MBD的基本定义[10]

定义 1 一个诊断系统DS是三元组(SD,CMP,OBS),其中SD表示系统描述；CMP是有限整数集合,表示系统中的元件；OBS表示系统行为的观察.其中SD和OBS一般用一阶句子集表示.

定义 2 对某个元件c(c∈CMP),谓词AB(c)表示其异常工作,而AB(c)则表示其正常工作.

定义3 一个组件集C是一个冲突当且仅当C⊆CMP且{SD∪OBS}∪{AB(c)|c∈CMP}是不可满足的.

定义4 一个组件集Δ是一个诊断当且仅当Δ⊆CMP且{SD∪OBS}∪{AB(c)|c∈CMPΔ}是一致的.

更进一步,Reiter提出诊断计算方法,即有如下定理:

定理1 一个组件集A是DS的一个诊断当且仅当A是DS所有冲突集的一个最小碰集.

2.2 基于MBD的软件错误定位

Robert Konighofer[3]等开发了一款基于MBD的程序错误定位和修复工具Forensic.Forensic以运行失效的程序及其规约作为输入,其中程序的规约既可以是程序断言,也可以是正确的参考程序,并且将程序中赋值语句的右值和条件语句视为元件.假设原失效程序为P,Forensic的错误定位由以下几个步骤来完成:

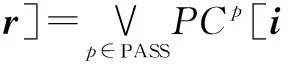
(1)

其中i表示输入符号向量,r是由cmp函数返回的一组不确定值,也称为修复符号向量.同时,在程序分析过程中,无论正确或失效的执行路径,对路径条件用约束求解得到一组输入值.

(3)诊断的计算.冲突的计算依赖Repair函数,其定义如下.

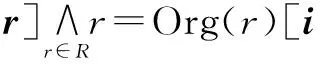
(2)

其中,R={r|CmpOf(r)∈Q},Q是元件的集合.

定义5 元件集Δ是P的一个诊断当且仅当Repair(CMPΔ)=true；元件集C(C⊆CMP)是P的一个冲突当且仅当Repair(C)=false.

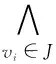
(3)

3 启发式实例

图1中的程序P是运行失效的,其中第4行的语句是错误的,应该是“res=y”.Forensic首先通过程序预处理识别出所有的元件集CMP={0,1,2,4,5,6},元件1,4是条件语句,而其他元件属于赋值语句的右值.然后,通过符号执行得到π[i‖r](表1)和一失败输入β={x=0,y=1,z=0}.表2列出了修复符号与其元件间的对应关系.最后,Forensic计算诊断即是构造碰集树的过程.Forensic首先从给定的输入β利用Repair′计算出一个冲突C1={1,2,3,4,6}(图2中的结点n0).根据冲突C1中的元件,以宽度优先,从左到右的顺序扩展分支和结点,最终得到一个指定深度的碰集树(图2所示).碰集树中的结点分为三类:(1) 用√ 标记的结点,它表示计算出的一个诊断；(2) 用×标记的结点为剪枝结点；(3) 内部结点,对应一个冲突.

表1 路径条件约束 π[i‖r]

π[k]ks15≥s02∧s15≥s01∧s15≥s00∧s14=0∧s07=00s16≥s02∧s16≥s01∧s16≥s00∧s14!=0∧s07=01s11≥s02∧s11≥s01∧s11≥s00∧s10=0∧s07!=02s12≥s02∧s12≥s01∧s12≥s00∧s10!=0∧s07!=03

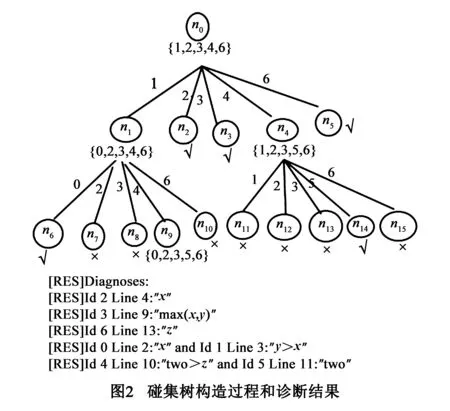
表2 修复符号与元件之间的对应关系

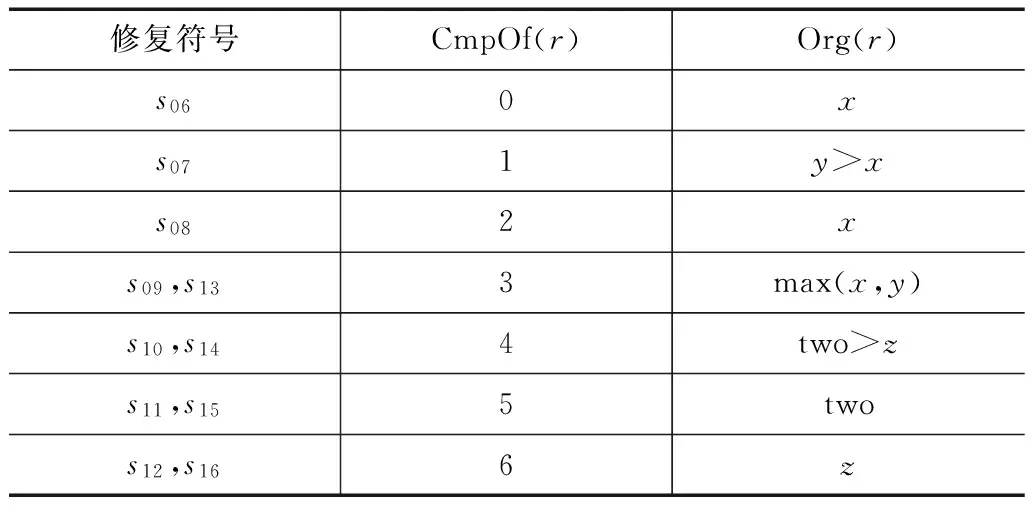
修复符号CmpOf(r)Org(r)s060xs071y>xs082xs09,s133max(x,y)s10,s144two>zs11,s155twos12,s166z

图2中给出最后诊断结果,即5个诊断,其中3个诊断的基是1,2个诊断的基是2.显然,除了第1个诊断以外,其他的诊断都属于假阳性.如本文引言所述,程序中的语句间往往存在数据与控制流依赖的,而MBD中诊断的计算是依赖于冲突的概念.但是冲突的概念并没有体现冲突中元件之间的依赖关系.根据定义5,冲突的存在即意味着公式不可满足.而Craig插值提供了一种更简单的形式展示两个公式不可满足的原因.因此存在着可能利用Craig插值表示形式去识别冲突中不相关的元件.例如,对于表1中第3条路径条件(k=3),对于冲突C1的两次分割点{{1,2},{3,4,6}},{{1,2,3},{4,6}},其对应的Craig插值是s08≤ 0,s09≤ 0,而这两个逻辑公式是语义等价的.这表明,元件3的执行与否不影响该条路径条件的不可满足性,即元件3是冗余的.图1中程序也反映到这一点,给定失败输入β,程序中第9行的赋值语句的值实际是来自第3行语句的值.

另一方面,程序中条件语句的取值非真即假.如果当某个条件语句无论取真或取假值都无法消除软件的失效,则可以认为该条件语句对于该软件运行失效是无相关.例如,对于表1中的π[3],元件4属于条件语句,所对应的分支约束条件是two>z.那么当前的失败输入β无论元件4取真或假,π[i‖r]仍然不可满足,即程序运行失效仍旧存在.因此,元件4是与当前失败输入软件失效无关的元件.

4 MBD的冲突中元件冗余分析

4.1 基于冲突的归纳Craig插值计算

定义6 Craig插值[15].给定公式φ1和φ2,如果φ1∧φ2是不可满足,则φ1和φ2的插值ψ有以下性质:(1)φ1|=ψ,(2)ψ∧φ2是不可满足的,(3)ψ中的符号仅与φ1和φ2中的符号有关.

为了叙述方便,引入一些符号.用Interp(φ1,φ2)表示逻辑公式φ1,φ2的Craig插值.用J表示测试用例集作为输入来进行错误诊断,且|J|=1.用π[k]表示π[i‖r]中某条路径条件,显然,若路径条件集合PASS且n=|PASS|,则k={0,1,…,n-1}.表1列出了图1中的程序所有合法的路径条件即π[i‖r].

冲突是元件的集合,为了对冲突中的元件进行冗余分析,必须先将冲突映射成路径条件中的逻辑公式.根据式(3),给定一冲突和失败输入集,最终一定可以获得一组不可满足的逻辑公式.首先,我们定义函数RepairSym,其将元件编号映射到修复符号.而Sym函数是将元件集合Q映射到的修复符号集合,即Sym(Q)=∪RepairSym(c),(c∈Q).显然,给定一个元件集和某路径条件,可以诱导出一个逻辑合取式,形式化描述如下.

定义7 给定一元件集Q和π[k](π[k]=T1∧T2∧…∧Tn),其中Ti为路径条件中的约束条件.则令Γ(Q,π[k])=∧Ti,其中Ti来自π[k]中的子句且Ti中使用了Sym(Q)中变量符号.

设冲突C={c1,c2,…,cn}和π[k],假设冲突中的元件是有序的.用F1,i,Fi+1,n表示冲突C可以分割成两个冲突子集,其中i的取值是1,2,…,n-1(i也称为分割点).对于每个分割点,就可以得到两个公式A=Γ(F1,i,π[k]),B=Γ(Fi+1,n,π[k]),且A∧B=⊥.令Ii=Interp(A,B),就可以构造一个Craig插值序列.

定义8 冲突的Craig插值序列.给定冲突C={c1,c2,…,cn}和π[k].Interps(C,π[k])={I1,I2,…,Ii,In-1}是C相对于π[k]的插值序列,其中i∈{1,2,…,n-1},且Ii=Interp(Γ(F1,i,π[k]),Γ(Fi+1,n,π[k])).

显然,计算出π[i‖r]中的每条π[k]路径条件的Craig插值序列,就可以得到一个Craig插值矩阵.表3列出的是图2中冲突{1,2,3,4,6}的Craig插值矩阵,其中,对于π[k],若Ii=false,则后继的Craig插值省略了,用“-”表示.在冲突中多个连续的分割点处,若存在语义等价(用符号“≡”表示)的Craig插值,则称为归纳Craig 插值.归纳Craig插值的存在表明在该分割点处所对应的元件的执行与否不影响π[k]不可满足,即可能存在冗余元件.

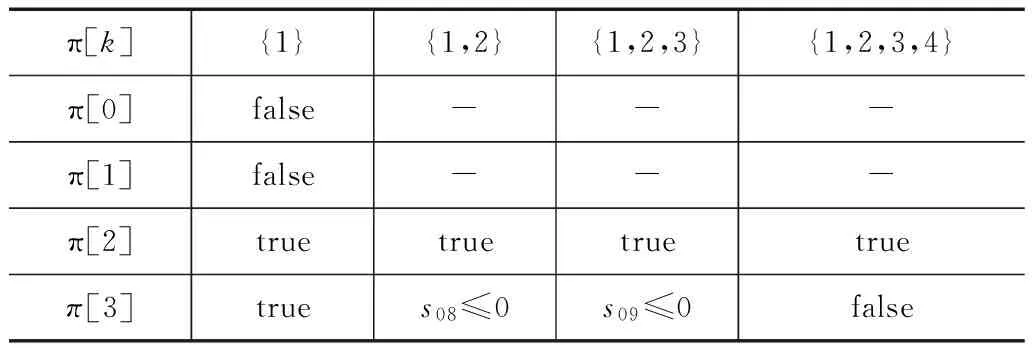
表3 冲突的Craig插值序列

定义 9 给定冲突C和π[k],设有Craig插值序列Interps(C,π[k])={I1,I2,…,Ii,In-1}.对于C的连续分割点i,j(j>i),若有Ii≡Ij,则称Ii对于分割点i,j是归纳Craig插值.

需要注意的是:

(1) Interps(C,π[k])中的归纳Craig插值可能不明显.例如,在表3中,对于π[3]中,虽然I2和I3不相同,但是语义等价,属于归纳Craig插值,因为根据表2中的元件3的原来值可知s09=s08.

(2) 归纳Craig插值具有传递性,即Ii≡Ii+1且Ii+1≡Ii+2,则Ii≡Ii+2.因此,对于多个连续的归纳Craig插值,除第一个以外的插值称为后继归纳Craig插值,用特殊值NULL标记(如表4).并且称第一个归纳Craig插值在冲突分割点所对应的元件为归纳Craig插值的起始元件.

(3) 对于Craig插值矩阵中的每个Interps(C,π[k])进行归纳插值计算后,就得到归纳Craig插值矩阵(表4).

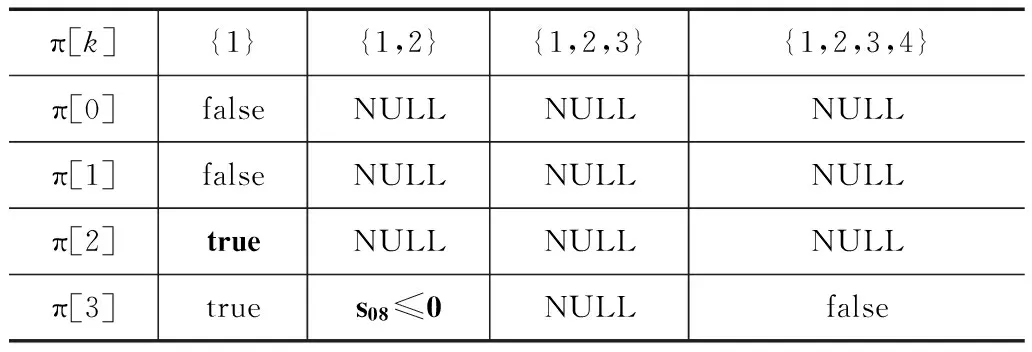
表4 对于表3,计算了归纳Craig插值后的插值序列

4.2 冲突中元件的过滤方法

4.2.1 基于归纳Craig插值元件的过滤方法

给定冲突C、归纳Craig插值矩阵M,若Interps(C,π[k])∈M中存在后继归纳Craig插值Ii时(即Ii=NULL),则冲突分割点i所对应的元件(用C[i]表示)可能为冗余元件.换言之,若Ii=NULL,删除冲突中的元件C[i]不会影响π[k]的不可满足性.但是删除元件C[i]可能会影响到其他路径条件π[s](s≠k)的不可满足性.因此必须给出条件判定后继归纳Craig插值所对应的元件是否为无相关冗余元件.

定义 10 给定冲突C={c1,c2,…,cn}和归纳Craig插值序列矩阵M,令Interps(C,π[k])= {I1,I2,…,Ii,In-1}∈M,若Ii=NULL且C[i]属于冗余元件,当且仅当对于Interps(C,π[s])(s≠k),C[i]不属于其中归纳插值的起始元件.

例如,在表4中,对于Interps(C,π[2]),I2=NULL,但是C[2]=元件2不能确定为无相关元件,因为对于Interps(C,π[3]),元件2是归纳Craig插值I2的起始元件.

4.2.2 无相关条件语句元件的过滤方法

考虑到给定具体的失败输入,其只能执行π[i‖r]中的某一条路径条件,且该路径条件的不可满足是违反程序合法行为模型造成的,而其他的路径条件的不可满足是因为其中的条件语句元件的分支约束不满足造成的.称路径条件中的条件语句元件的分支约束不满足的路径条件为非执行路径条件.下面的定义则给出了根据冲突的Craig插值序列识别非执行路径条件的方法.

定义11 设有冲突C={c1,c2,…,cn},π[i‖r],失败输入和Craig插值序列矩阵.对于某π[k],如果存在Craig插值Ii=false且C[i]为条件语句元件,则称π[k]对应于元件C[i]的非执行路径条件.

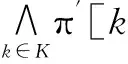
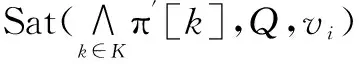
r=Org(r)[vi‖r]

(4)

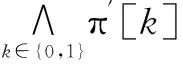
值得注意的是,这里只是说相对于失败输入β,元件1与程序失效无关.在利用多个失败输入进行错误定位的情况下,先可以对于每一个失败输入进行条件语句元件的不相关分析,得到相对于每一个失败输入的不相关条件语句元件集,然后,将所有不相关条件语句元件集进行求交集即得到相对于所有失败输入的不相关条件语句元件集.

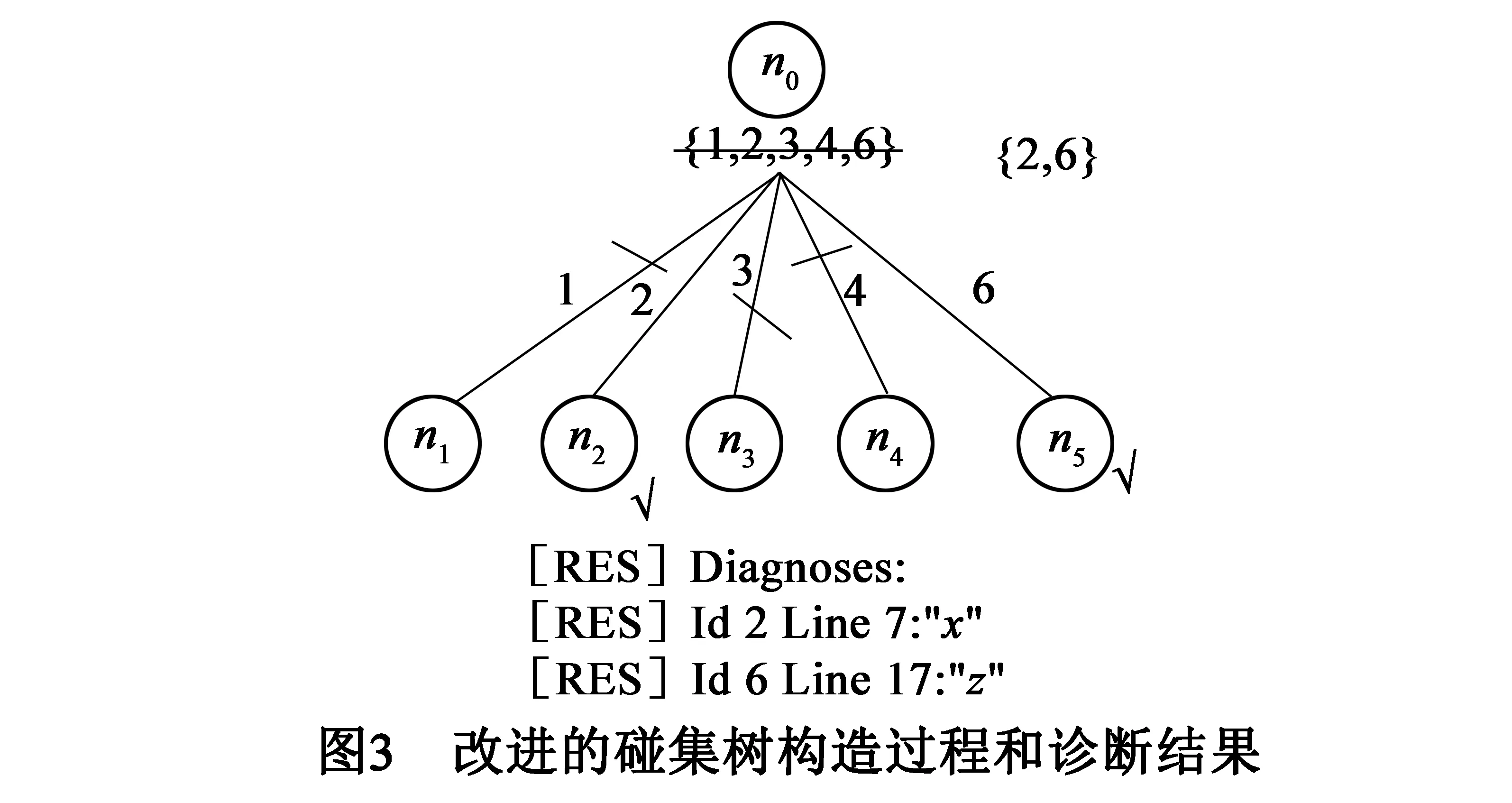
图3是将本文提出的冲突冗余元件分析方法应用到图1的过程所生成的碰集树.与Forensic的诊断结果相比较,诊断数从5个减少到2个,碰集树中的结点数从9个减少到3个.

5 相关算法

将上一节的思想表述成冲突元件过滤算法,该算法可以分三个步骤:

(1) 计算Craig插值序列矩阵数组

给定一个失败输入、冲突和π[i‖r],利用ComputeInterMatrix函数计算Craig插值序列矩阵.计算完所有失败输入所对应的插值序列矩阵就得到Craig插值序列矩阵数组.如算法1所示.

算法1 计算Craig插值序矩阵数组

输入:C={c0,c1,…,cn-1}:一个冲突,其中元件个数|C|

J={in0,in1,…,inn-1}:一个失败输入集合,总失败输入数|J|

π[i‖r]:程序合法行为模型,总的路径条件数|PASS|

输出:Craig插值序列的矩阵数组G

1. fors= 0;s< |J|;s++do

2. G[s] ← ComputeInterMatrix(π[i‖r],C,ini)

3. end for

(2) 无相关条件语句元件的过滤方法

对于算法1产生的每一个Craig插值序列矩阵,调用ComputeNEPath函数找出非执行路径条件集NE(K,c).对NE中的路径条件进行条件变更后利用Sat函数进行验证元件c对于当前失败输入是否属于无相关条件语句元件.所有的失败输入所对应的无相关条件语句元件的交集就是可以过滤的条件语句元件.具体内容见算法2.

算法2 无相关条件语句元件的过滤方法

输出:Removable :相对于所有失败输入的不相关条件语句元件集.

1. Removable ←φ

2. fori= 0;i< |J|;i++ do

3. Removed ←φ

4. NE(K,ci) ← ComputeNEPath(G[i],C) //ci∈C

5. 将NE中的π[k](k∈K)实现条件变更得到π′[k]

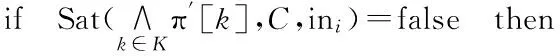
7.Removed←Removed∪ ci

8.endif

9.ifRemovable= φthen

10.Removable←Removed

11.else

12.Removable←Removable∩Removed

13.endif

14.endfor

(3)基于归纳Craig插值元件的过滤方法

首先调用ComputeInductiveInterp函数计算归纳插值矩阵.考察归纳插值矩阵中的每个Craig插值序列,对每个后继归纳插值根据定义10判断是否分割点处所对应的元件属于冗余元件,其中IsStartC函数检验某元件是否属于起始元件(如算法3所示).

显然,算法中的基本操作是可满足性计算或者计算Craig插值,则算法3的时间复杂度最大.而算法3在最坏情况下复杂度约为O(|PASS‖C‖J|),这也是整个算法时间复杂度.

算法3 基于归纳Craig插值元件的过滤方法

输出:完成过滤操作后的冲突.

1. fori= 0;i< |J|;i++ do

2. M [i] ← ComputeInductiveInterp(G[i])

3. end for

4. fori= 0;i< |J|;i++ do

5. for eachI=Interps(C,π[k])∈M [i]

6. forz=0;z<|C|-1;z++ do

7. ifIz=NULL and IsStartC(C[z])=false then

8. Removable ← Removable∪C[z]

9. end if

10. end for

11. end for

12. end for

13. return C-Removable

6 实验结果

为了验证本文方法(记PA)的有效性,在Forensic中实现了PA算法.采用Tcas的38个错误版本(Tcas有41个错误版本,但其他几个版本Forensic无法计算出诊断)作为实验对象将PA与Forensic进行比较研究.实验参数设置列在表5.表6列出了将PA与原Forensic方法应用到Tcas进行错误定位产生的诊断结果(对版本号v8,v16,v19,syb-ce-it分别设置为 200,400,200).从诊断总数来看,Forensic总体计算出254个诊断,而PA计算出131个诊断,诊断数减少了48.4%,其中,单元件诊断数减少率为22.9%,双元件诊断数减少率为66.4%.

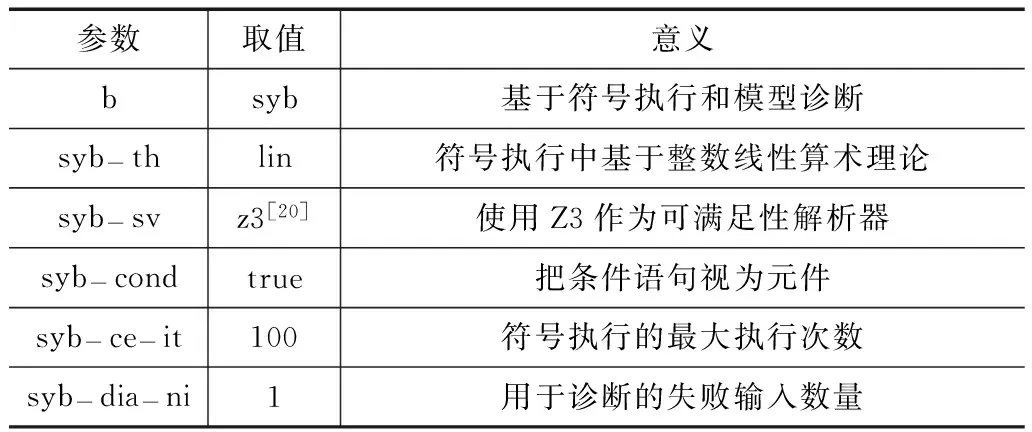
表5 实验参数设置

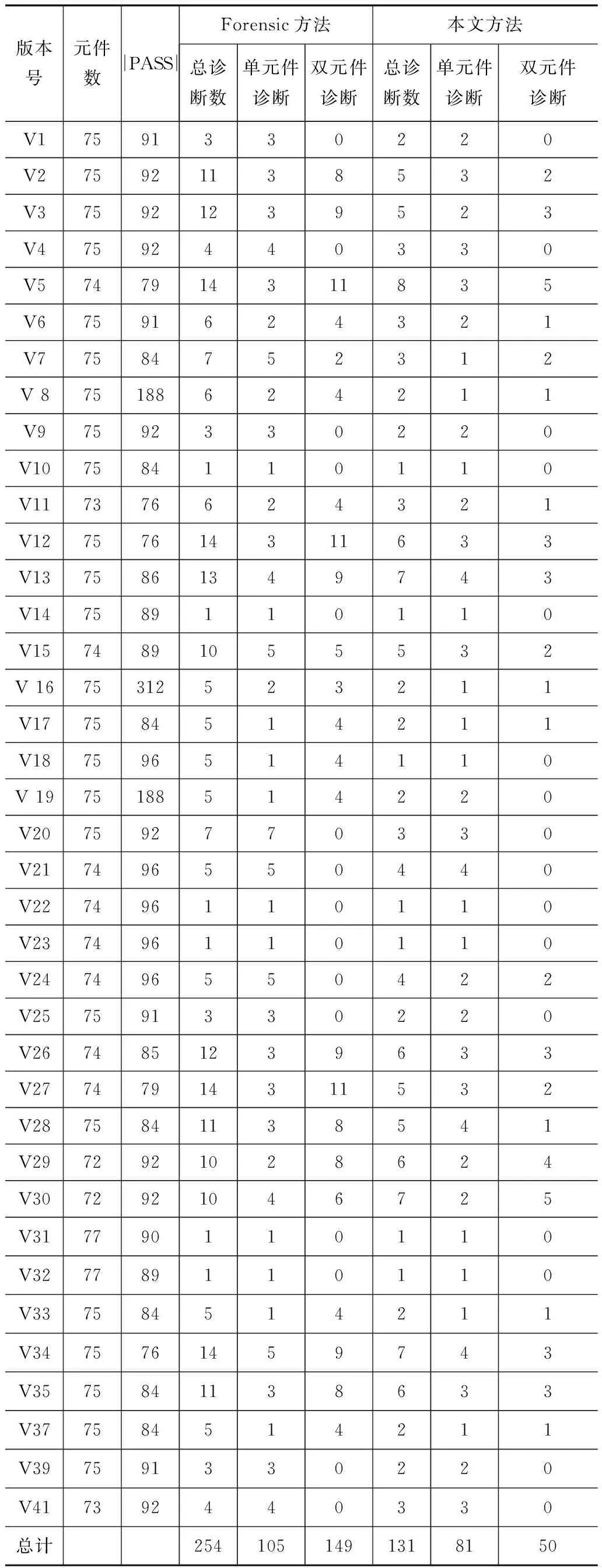
表6 Forensic与PA诊断结果的比较

采用Forensic方法,在诊断的计算过程中碰集树总体生成647个结点,而PA总体生成339个结点,结点的减少率为47.6%(图4).从平均数来看,原Forensic方法诊断计算平均生成17个结点,而本文方法平均生成9个结点.

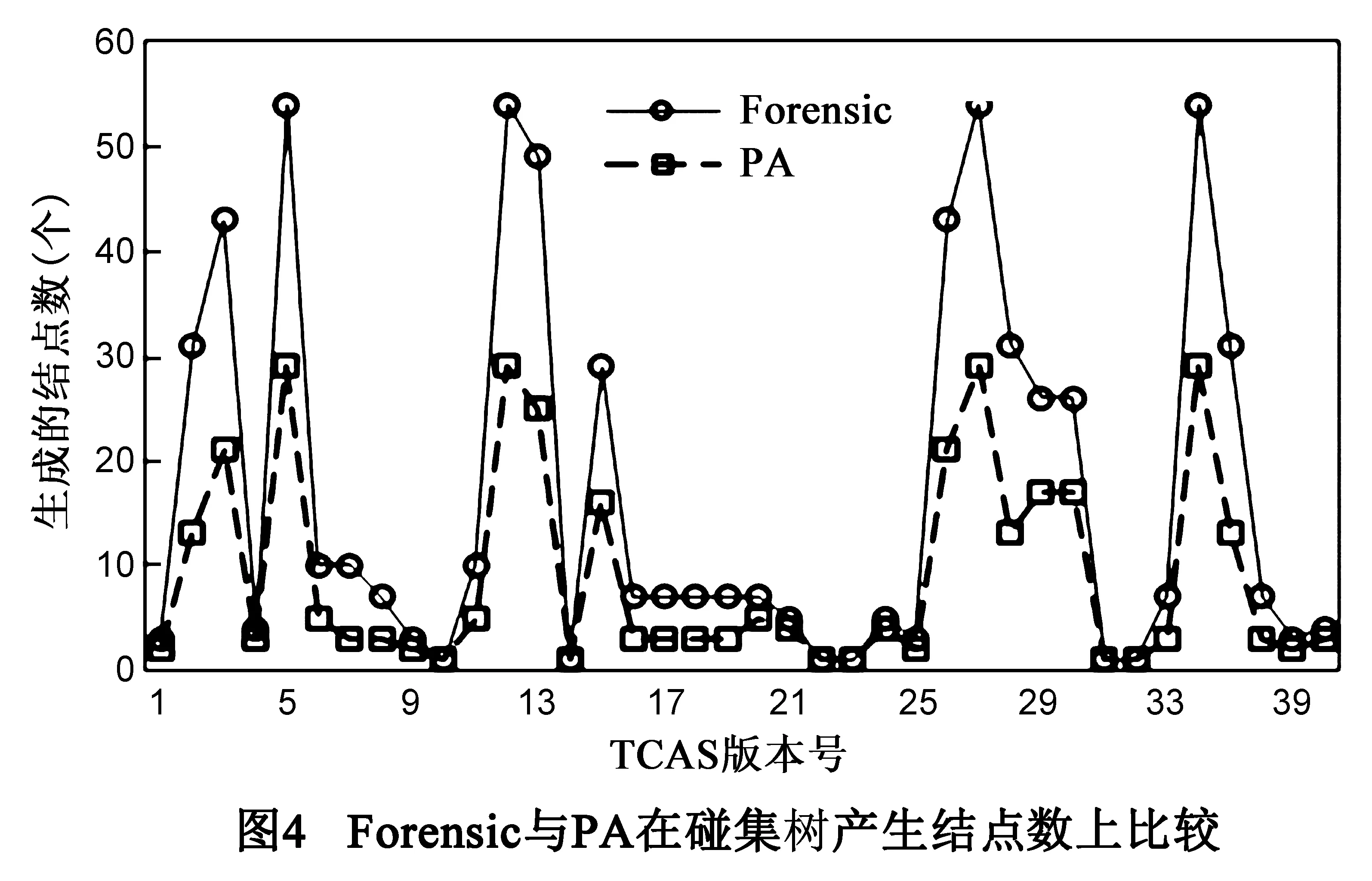
从诊断计算时间开销来看(图5),Forensic诊断计算总的时间花费是64.8s,而PA诊断计算花费是418.1s.显然,本文所提方法花费在诊断计算的时间是原Forensic方法的大约6倍.造成诊断计算时间增多的原因多次调用Z3进行Craig插值计算与可满足性判定.

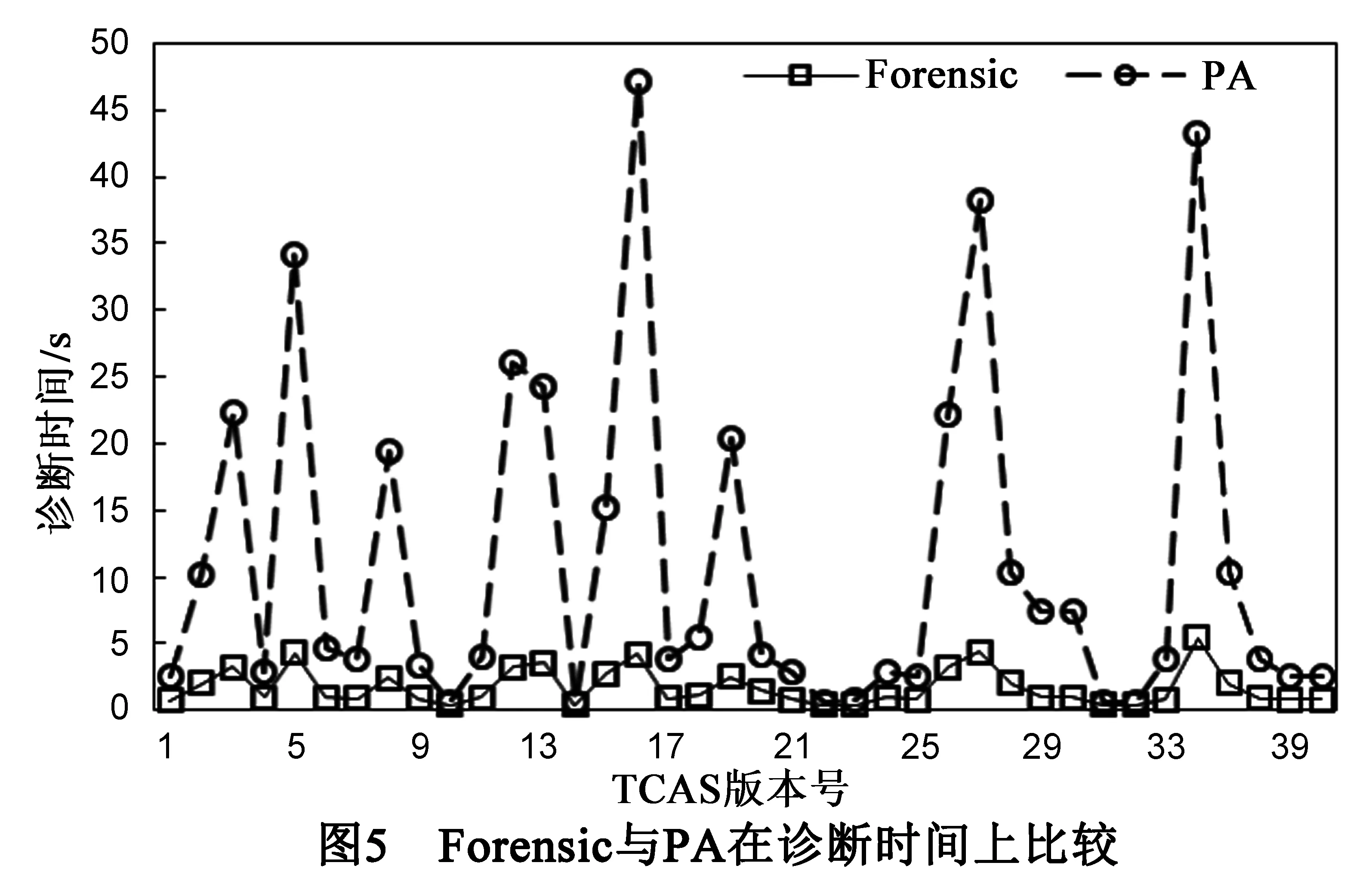
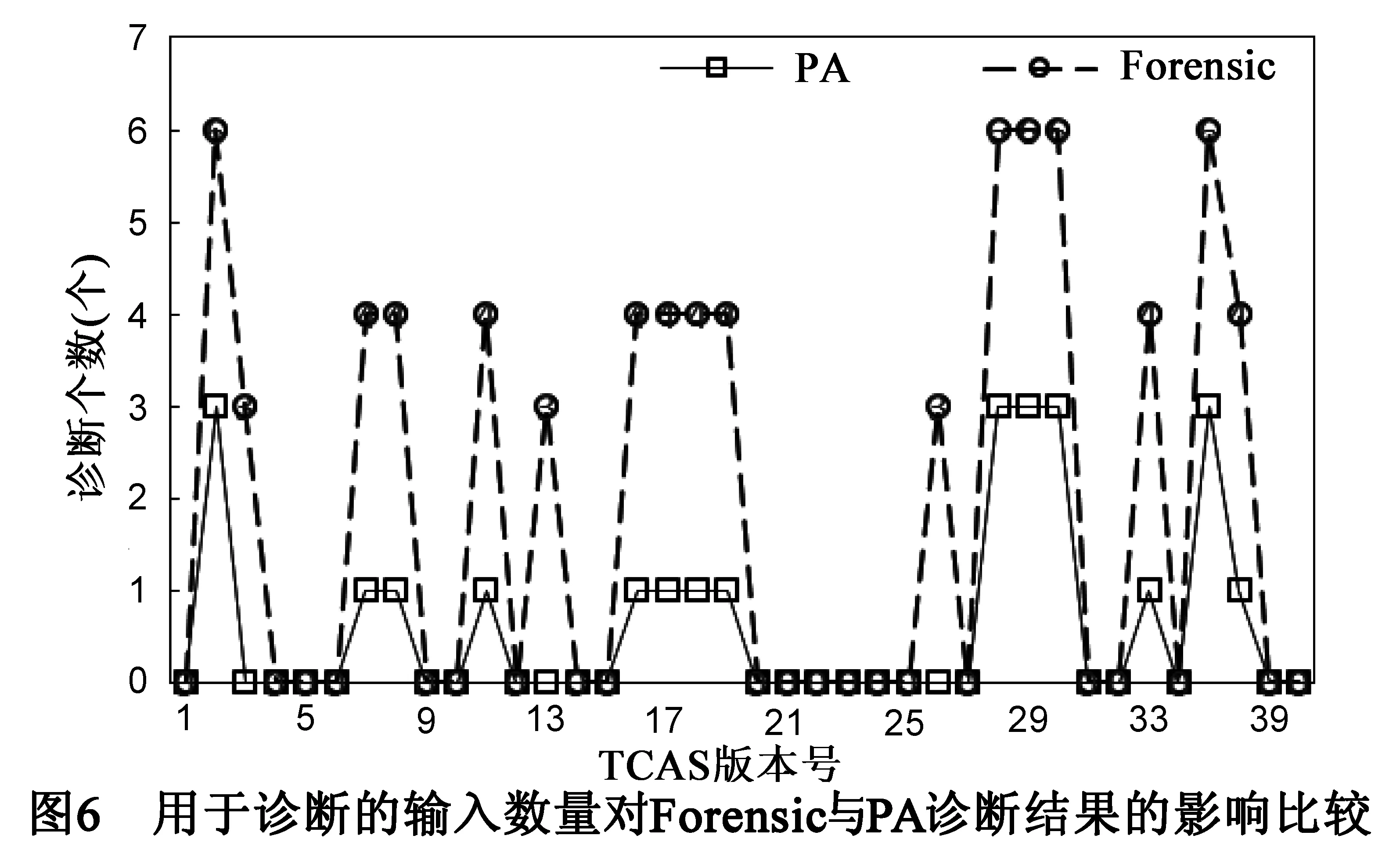
将syb-dia-ni参数取1和2时,对诊断数的差值进行比较(图6),显然,与Forensic相比,PA增加该参数的取值对诊断的诊断准确度的影响较小,也即是敏感度低于Forensic.

7 结语

本文分析了MBD软件错误定位中诊断假阳性的一些原因,并提出了一种冲突中冗余元件的分析方法.该方法既利用归纳的Craig插值去识别冲突中的冗余元件,同时能够清除无相关条件语句元件.实验结果表明该方法能够通过消除冲突的无相关元件,从而减少诊断的假阳性.下一步工作包括:更广泛地对本文所提方法进行实证研究.进一步结合其方法(比如基于统计错误定位方法,多层次的MBD诊断方法)对基于MBD软件错误定位方法进行优化改进.

[1]Lee Naish,Hua Jie Lee,Kotagiri Ramamohanarao.A model for spectra-based software diagnosis [J].ACM Transactions on software engineering and methodology (TOSEM) ,2011,20(3):11.

[2]Rui Abreu,Peter Zoeteweij,Rob Golsteijn,Arjan J C Van Gemund.A practical evaluation of spectrum-based fault localization [J].Journal of Systems and Software,2009,82(11):1780-1792.

[3]Konighofer R,Roderick Bloem.Automated error localization and correction for imperative programs [A].Formal Methods in Computer-Aided Design (FMCAD) [C].USA:IEEE,2011,91-100.

[4]Rui Abreu,Arjan J C Van Gemund.Diagnosing multiple intermittent failures using maximum likelihood estimation [J].Artificial Intelligence,2010,174(18):1481-1497.

[5]Chao Liu,Long Fei,Xifeng Yan,Jiawei Han,Samuel P Midkiff.Statistical debugging:A hypothesis testing-based approach [J].IEEE Transactions on Software Engineering,2006,32(10):831-848.

[6]Dennis Jeffrey,R Gupta.Effective and efficient localization of multiple faults using value replacement [A].IEEE International Conference on Software Maintenance [C].USA:IEEE,2009.221-230.

[7]Andreas Zeller,Ralf Hildebrandt.Simplifying and isolating failure-inducing input [J].IEEE Transactions on Software Engineering,2002,28(2):183-200.

[8]Swarup Kumar Sahoo,John Criswell,Chase Geigle,Vikram Adve.Using likely invariants for automated software fault localization [J].ACM SIGARCH Computer Architecture News,2013,41(1):139-152.

[9]王建峰,魏长安,盛云龙,等.基于错误交互集的组合测试软件故障定位方法[J].电子学报,2014,42(6):1173-1178.

WANG Jian-feng,WEI Chang-an,et al.Locating errors in combinatorial testing using set of possible faulty interactions [J].Acta Electronica Sinica,2014,42(6):1173-1178.(in Chinese)

[10]Raymond Reiter.A theory of diagnosis from first principles [J].Artificial intelligence,1987,32(1):57-95.

[11]Rui Abreu,Peter Zoeteweij,Arjan J C van Gemund.An observation-based model for fault localization [A].Proceedings of the International Workshop on Dynamic Analysis [C].USA:ACM,2008.64-70.

[12]Franz Wotawa,Mihai Nica,Iulia Moraru.Automated debugging based on a constraint model of the program and a test case [J].The Journal of Logic and Algebraic Programming,2012,81(4):390-407.

[13]Birgit Hofer,Franz Wotawa.Combining slicing and constraint solving for better debugging:The conbas approach [A].Advances in Software Engineering [C].Hindawi Publishing Corporation,2012.Article ID 628571.

[14]Jorg Weber, Franz Wotawa.Diagnosing dependent failures in the hardware and software of mobile autonomous robots [A].New Trends in Applied Artificial Intelligence [C].Berlin:Springer,2007.633-643.

[15]William Craig.Linear reasoning.a new form of the herbrand-gentzen theorem [J].The Journal of Symbolic Logic,1957,22(3):250-268.

[16]Evren Ermis,Martin Schaf,Thomas Wies.Error invariants [A].Lecture Notes in Computer Science:Formal Methods (Volume 7436) [C].Berlin:Springer,2012.187-201.

[17]陈祖希,徐中伟,霍伟伟,等.基于 Craig 插值的线性混成系统符号化模型检测[J].电子学报,2014,42(7):1338-1346.

CHEN Zu-xi,XU Zhong-wei,et al.Symbolic model checking for linear hybrid systems base on craig interpolation [J].Acta Electronica Sinica,2014,42(7):1338-1346.(in Chinese)

[18]Xiangyu Zhang,Neelam Gupta,Rajiv Gupta.Locating faults through automated predicate switching [A].Proceedings of the 28th International Conference on Software Engineering [C].USA:ACM,2006.272-281.

[19]Jurgen Christ,Evren Ermis,Martin Schaf,Thomas Wies.Flow-sensitive fault localization [A].Verification,Model Checking,and Abstract Interpretation [C].Brelin:Springer,2013.189-208.

[20]Leonardo De Moura,Nikolaj Bj?rner.Z3:An efficient smt solver [A].Tools and Algorithms for the Construction and Analysis of Systems [C].Berlin:Springer,2008.337-340.

徐 勇 男,1977年生,博士生,主要研究方向为软件工程、软件调试.

E-mail:xyus@whu.edu.cn

毋国庆 男,1954年生,教授、博士生导师,主要研究领域为软件需求工程、形式化方法.

E-mail:wgq@whu.edu.cn

Software Fault Localization Based on Model-Based Diagnosis Combined Craig Interpolant Analysis

XU Yong1,2,WU Guo-qing1,YUAN Meng-ting1

(1.ComputerSchool,WuhanUniversity,Wuhan,Hubei430072,China;2.SchoolofMathematicsandStatistics,ZhaoqingUniversity,Zhaoqing,Guangdong526061,China)

Model-based diagnosis,an intelligent diagnosis theory has been successfully applied in software fault localization with promising results.However,traditional MBD relies on the assumption that components in the system fail dependently which makes the diagnoses with high false positives in software fault localization.In this paper,a component redundancy analysis approach is presented.The approach not only uses Craig interpolant to filter redundant components,but also employs a fact that a branch predicate evaluates to either true or false to filter some branch condition components.Experimental results show that the proposed approach effectively reduces the false positive rates of diagnoses,i.e.,reducing the number of diagnosis by 48.4%,and reducing the number of nodes of hitting set tree generated during diagnosis computation by 47.6%.

model-based diagnosis (MBD); fault localization; redundancy analysis; Craig interpolant

2015-11-03；

2016-02-16；责任编辑:孙瑶

国家自然科学基金(No.91118003,No.61003071)；深圳战略性新兴产业发展专项资金(No.JCYJ20120616135936123)；中央高校基本科研业务费专项资金(No.3101046,No.201121102020006)

TP311

A

0372-2112 (2016)10-2514-08

��学报URL:http://www.ejournal.org.cn

10.3969/j.issn.0372-2112.2016.10.033